Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
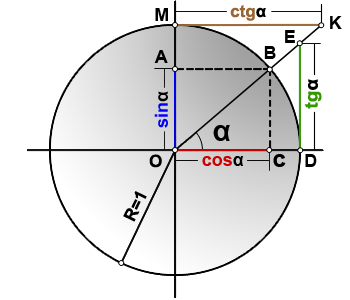
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
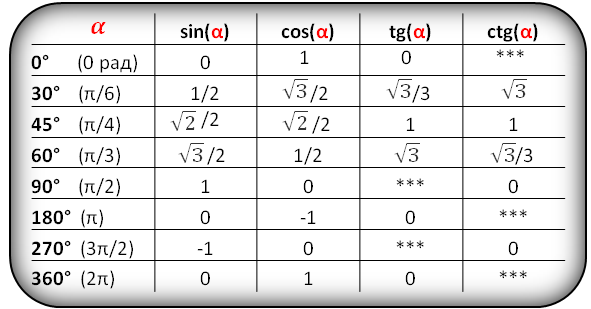
Значения функций для некоторых углов, α
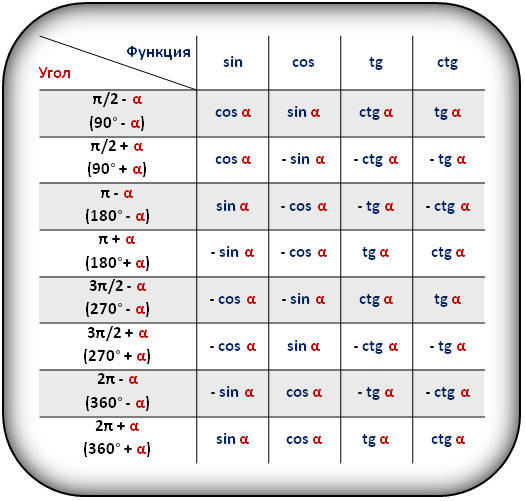
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
| tg(2α) = | 2tg(α)
1 – tg2(α) |
| ctg(2α) = | ctg2(α) – 1
2ctg(α) |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) < echo (Html::a(‘Войдите’, [‘/user/security/login’], [‘class’ =>»]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(Yii::$app->user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))< $name = Yii::$app->user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else < $name = »; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
28.01.17 / 22:14, Иван ИвановичОтветить -2
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Простейшие тригонометрические уравнения
п.1. Решение простейших тригонометрических уравнений
Про аркфункции (обратные тригонометрические функции) и их свойства – см. §9-11 данного справочника.
Обобщим результаты решения простейших уравнений, полученные в этих параграфах.
| Уравнение | ОДЗ | Решение |
| $$ sinx=a $$ | $$ -1leq aleq 1 $$ | begin x=(-1)^k arcsin a+pi kLeftrightarrow\ Leftrightarrow left[ begin x_1=arcsin a+2pi k\ x_2=pi-arcsin a+2pi k end right. end |
| $$ cosx=a $$ | $$ -1leq aleq 1 $$ | begin x=pm arccos a+2pi k end |
| $$ tgx=a $$ | $$ ainmathbb $$ | begin x=arctga+pi k end |
| $$ ctgx=a $$ | $$ ainmathbb $$ | begin x=arcctga+pi kLeftrightarrow\ Leftrightarrow x=arctgfrac1a+pi k end |
Частные случаи, для которых запись результата отличается от общей формулы:
| a=0 | a=-1 | a=1 | |
| $$ sinx=a $$ | $$ x=pi k $$ | $$ -fracpi2+2pi k $$ | $$ fracpi2+2pi k $$ |
| $$ cosx=a $$ | $$ x=fracpi2+pi k $$ | begin pi+2pi k end | begin 2pi k end |
| begin sinx=frac<sqrt<2>><2>\ x=(-1)^k arcsinfrac<sqrt<2>><2>+pi k=(-1)^kfracpi4+pi kLeftrightarrow left[ begin x_1=fracpi4+2pi k\ x_2=frac<3pi><4>+2pi k end right. end |
| begin ctgx=3\ x=arcctg3+pi kLeftrightarrow x=arctgfrac13+pi k end |
п.2. Решение уравнений с квадратом тригонометрической функции
К простейшим также можно отнести уравнения вида:
| Уравнение | ОДЗ | Решение |
| $$ sin^2x=a $$ | $$ 0leq aleq 1 $$ | begin x=pm arcsinsqrt+pi k end |
| $$ cos^2x=a $$ | $$ 0leq aleq 1 $$ | begin x=pm arccossqrt+pi k end |
| $$ tg^2x=a $$ | $$ ageq 0 $$ | begin x=pm arctgsqrt+pi k end |
| $$ ctg^2x=a $$ | $$ ageq 0 $$ | begin x=pm arcctgsqrt+pi k end |
| begin cos^x=frac14\ x=pm arccosfrac12+pi k=pmfracpi3+pi k end | begin tg^2x=1\ x=pm arctg1+pi k=pmfracpi4+pi k end |
п.3. Различные формы записи решений
Как известно, в тригонометрии все функции связаны между собой базовыми отношениями (см. §12 данного справочника). Если нам известна одна из функций, мы можем без труда найти все остальные. Преобразования в уравнениях приводят к тому, что решение может быть записано через любую из этих функций.
Кроме того, понижение степени или универсальная подстановка (см. §15 данного справочника) приводят к увеличению или уменьшению исходного угла в 2 раза, и ответ может оказаться очень непохожим на решения, полученные другими способами для того же уравнения.
| Решим уравнение (sin^2x=0,64) Для квадрата синуса решение имеет вид: begin x=pm arcsinsqrt<0,64>+pi k=\ =pm arcsin0,8+pi k end На числовой окружности этому решению соответствуют 4 базовых точки, которые можно представить по-разному: begin x=pm arcsin0,8+pi k=\ =pm arccos0,6+pi k=\ =pm arctgfrac43+pi k end |
Если решать уравнение с помощью формулы понижения степени, получаем: begin sin^2x=frac<1-cos2x><2>=0,64Rightarrow 1-cos2x=1,28Rightarrow cos2x=-0,28Rightarrow\ Rightarrow 2x=pm arccos(-0,28)+2pi kRightarrow x=pmfrac12 arccos(-0,28)+pi k end Если же решать уравнение с помощью универсальной подстановки: begin sin^2x=left(frac<2tgfrac<2>><1+tg^2frac<2>>right)^2=0,64Rightarrowfrac<2tgfrac<2>><1+tg^2frac<2>>=pm 0,8Rightarrow 1+tg^2frac<2>=pm 2,5tgfrac<2>Rightarrow\ left[ begin tg^2frac<2>+2,5tgfrac<2>+1=0\ tg^2frac<2>-2,5tgfrac<2>+1=0 end right. Rightarrow left[ begin left(tgfrac<2>+2right)left(tgfrac<2>+frac12right)=0\ left(tgfrac<2>-2right)left(tgfrac<2>-frac12right)=0 end right. Rightarrow left[ begin tgfrac<2>=pm 2\ tgfrac<2>=pmfrac12 end right. Rightarrow\ Rightarrow left[ begin x=pm arctg2+2pi k\ x=pm 2arctgfrac12+2pi k end right. end Таким образом, решая одно и то же уравнение, мы получаем очень разные по виду ответы. Однако, при проверке, все полученные множества решений совпадают.
п.4. Примеры
Пример 1. Решите уравнение обычным способом и с помощью универсальной подстановки. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin x=frac<sqrt<3>><2>)
| Обычный способ: begin x=(-1)^k arcsinfrac<sqrt<3>><2>+pi k=(-1)^kfracpi3 +pi k Leftrightarrow\ Leftrightarrow left[ begin x=fracpi3+2pi k\ x=frac<2pi><3>+2pi k end right. end 2 базовых точки на числовой окружности. |
Универсальная подстановка: begin sinx=frac<2tgfrac<2>><1+tg^2frac<2>>Rightarrow 1+tg^2frac<2>=frac<2tgfrac<2>><sqrt<3>/2>Rightarrow tg^2frac<2>-frac<4><sqrt<3>>tgfrac<2>+1=0\ D=left(-frac<4><sqrt<3>>right)^2-4=frac<16><3>-4=frac43, tgfrac<2>=frac<frac<4><sqrt<3>>pmfrac<2><sqrt<3>>><2>Rightarrow left[ begin tgfrac<2>=frac<1><sqrt<3>>\ tgfrac<2>=sqrt <3>end right. \ left[ begin frac<2>=fracpi6+pi k\ frac<2>=fracpi3+pi k end right. Rightarrow left[ begin x=fracpi3+2pi k\ x=frac<2pi><3>+2pi k end right. Leftrightarrow x=(-1)^kfracpi3+pi k end Ответы и множества решений совпадают.
Ответ: ((-1)^kfracpi3+pi k)
| Обычный способ: begin 2x=pm arccosfrac12+2pi kRightarrow\ x=pmfrac12left(arccosfrac12+2pi kright)=\ =pmfrac12cdotfracpi3+pi k=pmfracpi6+pi k end 4 базовых точки на числовой окружности. |
Универсальная подстановка: begin cos2x=frac<1-tg^2x><1+tg^2x>=frac12Rightarrow 2(1-tg^2x)=1+tg^2xRightarrow 3tg^2x=1Rightarrow tgx=pmfrac<1><sqrt<3>>\ x=pmfracpi6+pi k end Ответы и множества решений совпадают.
Ответ: (pmfracpi6+pi k)
в) (sinleft(frac<2>+fracpi3right)=1)
Обычный способ: begin frac<2>+fracpi3=fracpi2+2pi kRightarrow frac<2>=fracpi2-fracpi3+2pi k=fracpi6+2pi kRightarrow x=fracpi 3+4pi k end Одна базовая точка на числовой окружности с периодом (4pi).
Универсальная подстановка: begin sinleft(frac<2>+fracpi3right)=frac<2tgfrac<frac<2>+fracpi3><2>><1+tg^2frac<frac<2>+fracpi3><2>>=1Rightarrow tg^2left(frac<4>+fracpi6right)-2tgleft(frac<4>+fracpi6right)-2tgleft(frac<4>+fracpi6right)+1=0Rightarrow\ left(tgleft(frac<4>+fracpi6right)-1right)^2=0Rightarrow tgleft(frac<4>+fracpi6right)=1Rightarrow frac<4>+fracpi6=frac<pi><4>+pi kRightarrow\ Rightarrow frac<4>=fracpi4-fracpi6+pi kRightarrow frac<4>=frac<pi><12>+pi kRightarrow x=fracpi3+4pi k end Ответы и множества решений совпадают.
Ответ: (fracpi3+4pi k)
г*) (tgleft(3x+fracpi3right)=0)
Обычный способ: begin 3x+fracpi3=arctg0+pi k=pi kRightarrow 3x=-fracpi3+pi kRightarrow x=-fracpi9+frac<pi k> <3>end Универсальная подстановка: begin tgleft(3x+fracpi3right)=frac<2tgfrac<3x+fracpi3><2>><1-tg^2frac<3x+fracpi3><2>>=0Rightarrow tgfrac<3x+fracpi3><2>=0Rightarrowfrac<3x+fracpi3><2>=pi kRightarrow\ Rightarrow 3x+fracpi3=2pi k=3x=-fracpi3+2pi kRightarrow=-fracpi9+frac<2pi> <3>end При использовании универсальной подстановки потеряна половина корней (период увеличился в 2 раза). Это связано с тем, что мы отбросили еще одно решение: (tgfrac<3x+fracpi3><2>rightarrowinfty) — значение тангенса у асимптот. Действительно, в этом случае дробь стремится к 0, что удовлетворяет уравнению. Получаем: begin frac<3x+fracpi3><2>=fracpi2+pi kRightarrow 3x+fracpi3=pi+2pi kRightarrow 3x=frac<2pi><3>+2pi kRightarrow x=frac<2pi><9>+frac<2pi k> <3>end Таким образом, мы получили два семейства решений: begin left[ begin x=-fracpi9+frac<2pi k><3>\ x=frac<2pi><9>+frac<2pi> <3>end right. end Представим последовательности решений в градусах, подставляя возрастающие значения (k): begin left[ begin x=-20^<circ>+120^<circ>k=left<. -20^<circ>,100^<circ>,220^<circ>. right>\ x=40^<circ>+120^<circ>k=left<. 40^<circ>,160^<circ>,280^<circ>. right> end right. end Теперь представим полученное обычным способом решение в градусах: $$ x=-fracpi9+frac<pi k><3>=-20^<circ>+60^<circ>k=left<. -20^<circ>,40^<circ>,100^<circ>,160^<circ>,220^<circ>,280^<circ>. right> $$ Получаем, что: begin left[ begin x=-fracpi9+frac<2pi k><3>\ x=frac<2pi><9>+frac<2pi> <3>end right. Leftrightarrow x=-fracpi9+frac<pi k> <3>end Ответы и множества решений после учета значений у асимптот совпадают.
Ответ: (-fracpi9+frac<pi k><3>)
Вывод: при использовании универсальной подстановки нужно быть аккуратным и помнить о возможности потерять корни. Семейство бесконечных решений для тангенса (frac<2>=fracpi2+pi k), т.е. (x=pi+2pi k) нужно проверять как возможное решение для исходного уравнения отдельно.
При использовании универсальной подстановки можно потерять часть корней исходного тригонометрического уравнения.
Поэтому вместе с универсальной подстановкой проверяется также дополнительное возможное решение для бесконечного тангенса половинного угла: (x=pi+2pi k). begin f(sin(x), cos(x). )=0Leftrightarrow\ left[ begin fleft(tgleft(frac<2>right)right)=0\ (?) x=pi+2pi k end right. end где слева – исходное уравнение, а справа – универсальная подстановка и дополнительное возможное (не обязательное) семейство решений.
Пример 2. Решите уравнение обычным способом и с помощью формул понижения степени. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin^2x=frac34)
| Обычный способ: begin x=pm arcsinsqrt<frac34>+pi k=pm arcsinfrac<sqrt<3>><2>+pi k=pmfracpi3+pi k end |
Формулы понижения степени: begin sin^2x=frac<1-cos2x><2>=frac34Rightarrow 1-cos2x=frac32Rightarrow cos2x=-frac12Rightarrow\ Rightarrow 2x=pm arccosleft(-frac12right)+2pi k=pmfrac<2pi><3>+2pi kRightarrow x=pmfracpi3+pi k end Ответы и множества решений совпадают.
Ответ: (pmfracpi3+pi k)
| Обычный способ: begin 2x=pm arccossqrt<1>+pi k=pm 0+pi k=pi kRightarrow x=frac<pi k> <2>end Формулы понижения степени: begin cos^2 2x=frac<1+cos4x><2>=1Rightarrow 1+cos4x=2Rightarrow\ cos4x=1Rightarrow 4x=0+2pi k=2pi kRightarrow x=frac<pi k> <2>end |
Ответы и множества решений совпадают.
Ответ: (frac<pi k><2>)
| Обычный способ: begin frac<2>+fracpi3=pm arcsinsqrt<frac14>+pi k=pm arcsinfrac12+pi=pmfracpi6+pi k\ frac<2>=-fracpi3pmfracpi6+pi k= left[ begin fracpi2+pi k\ -fracpi6+pi k end right. Rightarrow x= left[ begin -pi+2pi k\ -fracpi3+2pi k end right. end |
Формулы понижения степени: begin sin^2left(frac<2>+fracpi3right)=frac<1-cosleft(2left(frac<2>+fracpi3right)right)><2>=frac14Rightarrow 1-cosleft(x+frac<2pi><3>right)=frac12Rightarrow\ Rightarrow cosleft(x+frac<2pi><3>right)=frac12Rightarrow x+frac<2pi><3>=pm arccosleft(frac12right)+2pi kRightarrow\ Rightarrow x=-frac<2pi><3>pmfracpi3+2pi k= left[ begin -pi+2pi k\ -fracpi3+2pi k end right. end Ответы и множества решений совпадают.
Ответ: (-pi+2pi k, -fracpi3+2pi k)
| Обычный способ: begin x+fracpi4=pm arctgsqrt<1>+pi k=pmfracpi4+pi kRightarrow\ Rightarrow x=-fracpi4pmfracpi4+pi k= left[ begin -fracpi2+pi k\ pi k end right. end |
Формулы понижения степени: begin cos^2left(x+fracpi4right)=frac<1><1+underbrace_<=1>>=frac12\ cos^2left(x+fracpi4right)=frac<1+cosleft(2left(x+fracpi4right)right)><2>=frac12 Rightarrow cosleft(2x+fracpi2right)=0Rightarrow\ Rightarrow -sin2x=0Rightarrow sin2x=0 Rightarrow 2x=pi kRightarrow x=frac<pi k> <2>end Из чертежа видно, что begin left[ begin -fracpi2+pi k\ pi k end right. Leftrightarrow x=frac<pi k> <2>end Оба решения соответствуют 4 базовым точкам на числовой окружности через каждые 90°. Множества решений совпадают. Ответы не совпадают, но являются равнозначными.
Ответ: (frac<pi k><2>)
Вывод: формулы понижения степени не расширяют и не урезают множество корней исходного уравнения. Полученные ответы либо совпадают, либо нет, но всегда являются равнозначными.
sin^2x (уравнение)
Найду корень уравнения: sin^2x
Решение
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_ <1>= frac <sqrt- b><2 a>$$
$$w_ <2>= frac <- sqrt- b><2 a>$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 0$$
, то
Т.к. D = 0, то корень всего один.
$$w_ <1>= 0$$
делаем обратную замену
$$sin <left(x right)>= w$$
Дано уравнение
$$sin <left(x right)>= w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 pi n + operatorname<left(w right)>$$
$$x = 2 pi n — operatorname <left(w right)>+ pi$$
Или
$$x = 2 pi n + operatorname<left(w right)>$$
$$x = 2 pi n — operatorname <left(w right)>+ pi$$
, где n — любое целое число
подставляем w:
$$x_ <1>= 2 pi n + operatorname <left(w_<1>right)>$$
$$x_ <1>= 2 pi n + operatorname<left(0 right)>$$
$$x_ <1>= 2 pi n$$
$$x_ <2>= 2 pi n — operatorname <left(w_<1>right)> + pi$$
$$x_ <2>= 2 pi n — operatorname <left(0 right)>+ pi$$
$$x_ <2>= 2 pi n + pi$$
http://reshator.com/sprav/algebra/10-11-klass/prostejshie-trigonometricheskie-uravneniya/
http://www.kontrolnaya-rabota.ru/s/equal-one/any-uravnenie/expr/c4c4da1b6c596ccad0335d4493abe39e/
Кватернионы в анизотропном пространстве, дополнение: nabbla1 — LiveJournal
Продолжение этого.
Пожалуй, для моих задач наиболее удачной была бы следующая формулировка:
При этом нормой кватерниона будем считать
И тогда поворот вектора при помощи кватерниона сведётся к следующей матрице поворота:
Меня несколько сбило с толку, что отличие от оригинальной матрицы поворота — всегда в сторону уменьшения коэффициентов!
Да и при умножении кватернионов то же самое: мы считаем, что все значения от -1 до +1, но при этом никогда не появляется сдвигов влево (умножений на 2), исключительно сдвиги вправо!
Это казалось неверным. Ведь если мы производим вращения в пространстве, где оси имеют разный масштаб, то, грубо говоря, первый поворот, переводящий Y в X, должен будет уменьшить значение вдвое, зато обратный к нему — напротив, увеличить вдвое! Кажется, что «умножалка на 2» где-то должна сидеть!
В конце концов, когда мы посмотрели, как преобразуется матрица поворота от изменения масштаба оси, там отчётливо появлялись коэффициенты 2 в одном месте и 1/2 в другом.
Тем не менее, похоже всё сходится…
Первая хитрость в том, что мы ограничили «силу» тех кватернионов, которые ведут к существенному возрастанию координат!
К примеру, у нас был вектор (1;0;0), при том ось X имеет вдвое бОльшую цену деления, чем все остальные, т.е 1 по оси X — это строго 1 метр, а такая же 1 по оси Y — это 0,5 метра.
При этом подобный масштаб справедлив и для кватернионов. Кватернион i, т.е соотв. вектору (0;1;0;0) соответствует вращению вокруг оси X на 180 градусов, а кватернион j, или (0;0;1;0) — вообще не является кватернионом вращения, поскольку его норма равна всего лишь 1/2…
Собственно, самый крупный кватернион вращения вокруг оси Y, который мы можем записать, используя значения от -1 до +1 — это
Его норма (по формуле, данной выше) равна единице!
И выражает этот кватернион поворот на угол 60° вокруг оси Y, что даёт матрицу поворота:
И если этот поворот применить к вектору (1;0;0), получится первый столбец этой матрицы, со значением Z больше единицы по абсолютной величине.
Ранее у нас выполнялось соотношение, что векторы длиной 1, поворачиваемый с помощью кватернионов с единичной нормой, сохраняют свою длину, и если все коэффициенты принимают значения от -1 до +1, то вектор длины 1 заведомо может быть записан!
Но здесь у нас и длина вектора, и норма кватерниона приобретают коэффициент 1/4 для осей Y,Z. Для них всё это остаётся в силе, длина остаётся неизменной, как это и положено при повороте.
Вот только гарантий насчёт того, что вектора влезут в те значения -1..+1, которые выделены им в компьютере — уже нет. Ведь если просто найти корень из суммы квадратов компонентов нашего кватерниона, это получится не 1, а вовсе даже 1,32. А вектор во время поворота кватернионом может возрасти на КВАДРАТ НОРМЫ, т.е и вовсе 1+3/4 = 1,75. И в тех компонентах матрицы, которые никак не поменялись по сравнению с оригинальной, так и вышло… Вот у нас корень из 3 выскочил, который 1,73. Это вторая хитрость.
Что-то в этом есть… Хотя пока не буду торопиться с применением, оставлю это в качестве задела на будущее.
Но пока эта идея кружилась в голове, я просто обязан был её изложить на бумаге и в уютном бложеке, чтобы голова освободилась под более полезные на данный момент вещи.
Path to Nowhere – Полезная информация для новых игроков
Path to Nowhere – это новый проект от студии AISNO Games, который был недавно выпущен для общего доступа. Новая RPG получила положительный отклик от игроков, собрав более 1 миллиона загрузок за первые 3 дня с момента запуска. Path to Nowhere доступна для бесплатного скачивания в Google Play Store и App Store. На старте игры вас будут ждать подарки в виде 10 билетов для призыва, 1 эксклюзивного скина и много премиальной валюты.
Проще говоря, Path to Nowhere — это, которая использует механику гача. Вы сможете собрать свою коллекцию героев, которых называют Грешниками. С помощью Грешников вы отправитесь в сражения против монстров. Все действия игрового процесса происходят на небольшой карте, которая разделена на несколько квадратов, причем каждый квадрат представляет собой 1 область передвижения как для союзников, так и для врагов. Мы еще поговорим более подробно про этот игровой аспект.
В этой статье по Path to Nowhere мы расскажем про основные моменты в игре и поделимся важной информацией, которую нужно знать каждому новому игроку. Пользователям, которые уже приступили и начали свой путь в игре, эта статья тоже может быть полезной. Проект относительно новый и каждый день вы будете находить все больше новой информации, поэтому не стоит ограничиваться информацией только из этой статьи.
- Система призыва
- Боевая механика
- Прокачка Грешников
- Миссии в игре
Система призыва
В Path to Nowhere присутствует система гача. Каждый герой имеет свою вероятность выпадения и игрокам предстоит собрать свою коллекцию персонажей. Игроки могут получить новых персонажей с помощью специальной системы, которая становится доступной после прохождения обучения. Чем выше уровень редкости персонажа, тем ниже шансы его выпадения. Правило довольно стандартное и его можно встретить во многих проектах подобного жанра.
В игре есть несколько уровней редкости:
- Персонажи уровня S – шанс призыва 2%
- Персонажи уровня A – шанс призыва 2%
- Персонажи уровня B – шанс призыва 2%
Игроки могут получить Грешников с помощью специальных баннеров.
- Sin and Order Beginner Summoning Banner – Это специальный баннер, который доступен всем новым игрокам. В этом баннере игроки гарантированно получат Грешника уровня S в первых 10 призывах. Кроме того, игроки могут сделать до 20 призывов на этом баннере. Каждый 10 призыв стоит немного дешевле, чем другие. Имейте в виду, что на этом баннере доступно ограниченное количество Грешников уровня S. Он идеально подходит для игроков, которые будут выполнять реролл.
- Routine Summoning Banner – через этот баннер игроки могут вызывать грешников ранга R-S, используя специальную валюту. На этом баннере доступны все Грешники из игры.
- Regular Summoning Banner – через этот баннер игроки могут вызывать грешников ранга R-S, используя специальную валюту. Этот баннер содержит всех Грешников, доступных в игре.
Также в игре есть различные валюты призыва:
- Warrant – это основная валюта, используемая для призыва на всех доступных баннерах в Path to Nowhere.
Игроки могут получить их из внутриигровых событий, наград за прохождение основного сюжета и путем покупки в магазине.
В Path to Nowhere существует система гаранта, которая упрощает игровой процесс для больше части игроков. Вероятность выпадения Грешников уровня S увеличивается до 2,84%, если игроки не вызвали персонажа этого уровня за 50 призывов. Если игрокам не удастся призвать Грешника S-ранга за 79 попыток, то 80-й призыв гарантированно даст вам Грешника S уровня. Мы рассказали про самых сильных грешников в Path to Nowhere в этой статье.
Боевая механика
Боевую систему Path to Nowhere не так уж сложно понять. Как мы ранее говорили, вся карта разделена на несколько квадратов, каждый из которых представляет собой область перемещения, где могут находиться как союзники, так и враги. Главное отличие между вражеской и вашей командой заключается в том, что у вас есть определенные ограничения в передвижении по полю боя. Обычно вся карта отмечена крестиками, которые представляют область.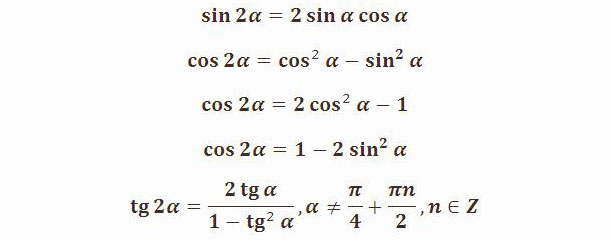
Игроки должны сформировать группу из 6 разных грешников, которые будут размещены на карте. Перед началом каждого боя у вас будет возможность посмотреть карту, чтобы спланировать свои действия. Грешники атакуют врагов автоматически, когда они находятся в пределах радиуса атаки. Некоторые Грешники специализируются только на атаках ближнего боя, а другие на атаках дальнего боя. Игроки должны иметь хорошее сочетание персонажей в своей команде и учитывая особенности каждой стадии. Каждый игрок может самостоятельно использовать особое умение Грешника в любой момент сражения.
Прокачка Грешников в Path to Nowhere
Чувствуете, что застряли на каком-то определенном этапе и перепробовали уже все, что можно? Что ж, существует большая вероятность того, что вам не хватает силы и дополнительных характеристик, необходимых для прохождения конкретного этапа. Path to Nowhere — это игра в которой характеристики персонажей очень важны и играют основную роль в прохождении основной истории. Грешники с более высокий уровнем редкости будут иметь сильные базовые характеристики по сравнению с другими персонажами.
- Прокачка уровня
- Повышение
- Кандалы
- Прокачка навыков
Прокачка уровня – это один из лучших способов увеличения базовых характеристик Грешников. Под базовой статистикой мы подразумеваем уровень атаки, защити и HP, которые вы видите, когда заходите в их профиль. Игроки могут повысить уровень своих Грешников через специальное меню с помощью определенных ресурсов. Каждый Грешник получает определенное количество очков, чтобы повысить свой уровень. Чем выше уровень, тем больше ресурсов вам потребуется для улучшения персонажа. Чтобы снять ограничение по уровню, вам необходимо повысить Грешника. Например, первое ограничение даст вам прокачать персонажа только до 20 уровня.
Скачать Path to Nowhere на ПК
Повышение – игроки могут улучшить своих героев и снять ограничение на прокачку уровня с помощью этого метода. Новые уровни открывают различные способности и пассивные эффекты для Грешника, что также повышает их эффективность использования. Продвижения делятся на Фазы. 1-я фаза увеличивает максимальный предел уровня с 20 до 40. 2-я фаза увеличивает максимальный предел уровня с 40 до 70. 3-я фаза увеличивает максимальный предел уровня с 70 до 90. 1-я фаза открывает новый пассивный навык для Грешника. 2-я фаза также открывает новую пассивную способность для Грешника. 3-я фаза открывает новый скин, а также их эксклюзивный слот. Для повышения вам потребуются специальные ресурсы, которые можно найти в подземельях.
Кандалы
– это механика, с помощью которой игроки могут улучшить навыки своих Грешников, предоставляя им дополнительную статистику.
Прокачка навыков – это еще один способ увеличить их эффективность. Этот способ улучшения сосредоточен на навыках и позволяет увеличить урон наносимый Грешником. Навыки можно улучшить, с помощью специальной валюты. Вы сможете без проблем ее получить. Некоторые навыки могут быть улучшены только после того, как грешник достигнет определенной фазы.
Миссии в игре
В Path to Nowhere миссии привязаны к системе Battle Pass, где игроки могут выполнять миссии и зарабатывать опыт для прохождения уровней. Миссии в игре называются Surveillance Order и разделены на 3 разных типа:
Ежедневные миссии
Игроки могут выполнять эти миссии ежедневно, чтобы заработать хорошие награды и очки опыта. В игре есть разные миссии. Вот их список и награды за их выполнение:
- Вход в игру – Management Points x 10 + Surveillance Data x 50
- Пркоачайте Грешников – Management Points x 10 + Surveillance Data x 50
- Купите любой товар – Management Points x 10 + Surveillance Data x 50
- Завершите один уровень в локации Oblivion Pit – Management Points x 10 + Surveillance Data x 100
- Получите награду – Management Points x 10 + Surveillance Data x 50
- Пройдите испытание Stormy Memories – Management Points x 10 + Surveillance Data x 100
- Отправьте посылку– Management Points x 10 + Surveillance Data x 50
- Потратьте 100 очков выносливости – Management Points x 10 + Surveillance Data x 50
- Потратьте 300 очков выносливости – Management Points x 10 + Surveillance Data x 100
Еженедельные миссии
Игроки могут выполнять эти миссии еженедельно, чтобы заработать награды и очки опыта.
В игре есть разные миссии. Вот их список и награды за их выполнение:
- Купите любой товар – Management Points x 10 + Surveillance Data x 50
- Потратьте 1000 очков выносливости – Assessment Points x 10 + Surveillance Data x 375
- Потратьте 2000 очков выносливости – Assessment Points x 20 + Surveillance Data x 675
- Соберите награду 20 раз – Assessment Points x 10 + Surveillance Data x 375
- Участвуйте в испытании Broken Frontline 3 раза – Assessment Points x 10 + Surveillance Data x 775
- Участвуйте в испытании Broken Frontline 9 раз – Assessment Points x 20 + Surveillance Data x 775
- Завершите любую главу Oblivion Pit – Assessment Points x 10 + Surveillance Data x 775
- Завершите любую главу Oblivion Pit 3 раза – Assessment Points x 20 + Surveillance Data x 775
- Помогите любому члену Тайного общества 3 раза – Assessment Points x 10 + Surveillance Data x 350
- Отправьте посылку 3 раза – Assessment Points x 20 + Surveillance Data x 450
- Отправьте посылку 15 раз – Assessment Points x 5 + Surveillance Data x 450
- Начислите очки дружбы 20 раз – Assessment Points x 5 + Surveillance Data x 500
На этом мы заканчиваем нашу статью.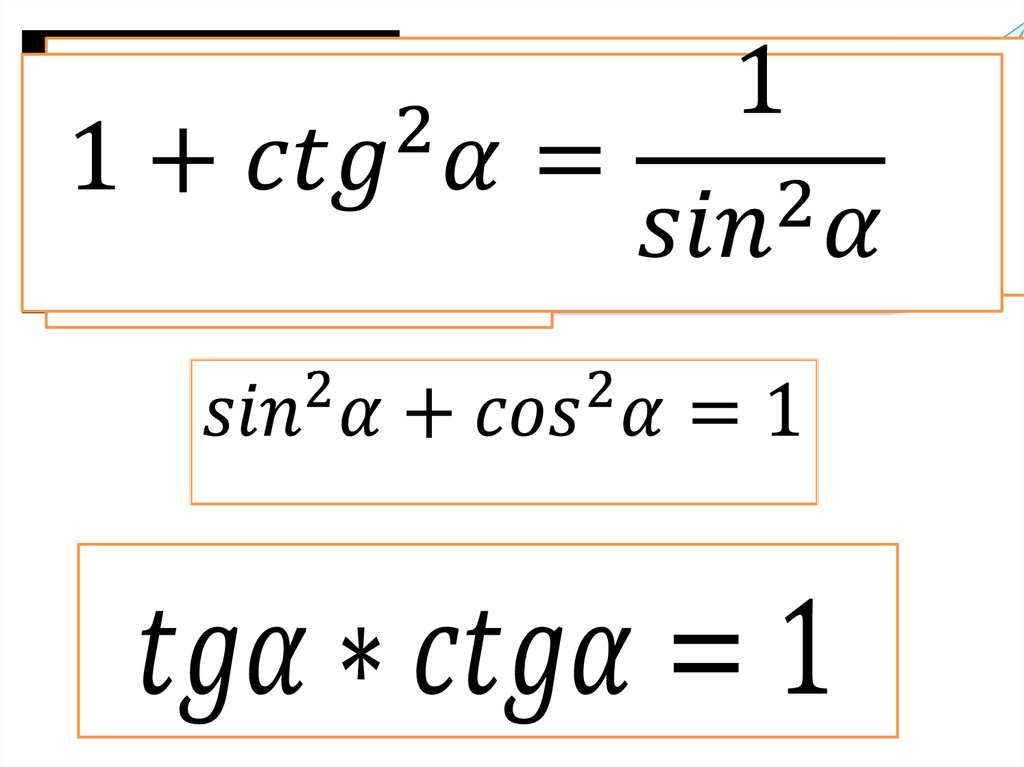
Я обычно говорю «синус в квадрате $x$», и люди понимают мою мысль.
$endgroup$
$begingroup$
Я из Швеции, но у меня математика на английском языке, так что, надеюсь, будет то же самое. Мы бы сказали здесь «грех в квадрате х», однако в реальных англоязычных странах это может быть иначе.
$endgroup$
$begingroup$
Как насчет квадрата синуса x? 92(х)$. Я предпочитаю «синус х квадрат».
$endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
График квадрата синуса (x)
График квадрата синуса (x) | mathtestpreparation.com
вернуться к математический вопрос и ответ
- Шаг 1: Найдите выражение sin 2 x
- Используя формулы двойного угла: cos 2x = cos 2 x — sin 2 x , обозначьте его как уравнение (1)
- Используя тождества Пифагора: sin 2 x + cos 2 х = 1
- Подставьте cos 2 x = 1 — sin 2 x в уравнение (1), затем
- cos 2x = 1 — sin 2 x — sin 2 x
- cos 2x = 1 — 2sin 2 x .
- Выразите sin 2 x в левой части уравнения, затем
- 2sin 2 x = 1 — cos 2x , разделить коэффициент 2 в каждом пункте уравнения
- sin 2 x = 1/2 — (1/2)cos 2x
- таким образом, получим выражение sin 2 x
- Шаг 2: Нарисуйте график y = (1/2)cos 2x
- Примечание.
Для функции периода y = A cos (Bx + C) ее амплитуда равна A. Период T = 2 pi/B и фазовый сдвиг равен C.
- В этом случае его амплитуда A = 1/2, период T = 2 pi/2 = pi и фазовый сдвиг C = 0
- Шаг 3: Нарисуйте график y = — (1/2)cos 2x
- Отразите график y = (1/2)cos2x по оси x, чтобы получить график y = — (1/2)cos2x
- Шаг 4: Нарисуйте два графика, например y 1 = 1/2 и y 2 = -(1/2)cos2x, чтобы сложить их.
- Когда x = 0, y=1/2 + (-1/2)cos2x = 1/2 + (- 1/2) = 0
- Когда x = pi/4, y=1/2 + (-1/2)cos2x = 1/2 + 0 = 1/2
- Когда x = pi/2, y=1/2 + (-1/2)cos2x = 1/2 + 1/2 = 1
- Когда x = 3pi/4, y=1/2 + (-1/2)cos2x = 1/2 + 0 = 1/2
- Когда x = pi, y=1/2 + (-1/2)cos2x = 1/2 + (- 1/2) = 0
- Когда x = 5pi/4, y=1/2 + (-1/2)cos2x = 1/2 + 0 = 1/2
- Когда x = 3pi/2, y=1/2 + (-1/2)cos2x = 1/2 + 1/2 = 1
- Когда x = 7pi/4.
Синус в квадрате
Синус (sin) — это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
sin 2 (x)=sin(x)*sin(x)
Значение синуса находится в диапазоне от -1 до +1.
Смотрите также калькулятор вычисления синуса угла.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.

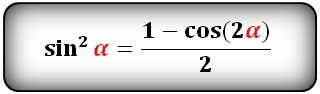
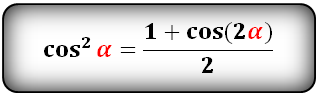
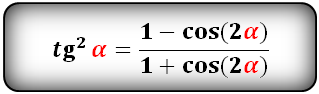
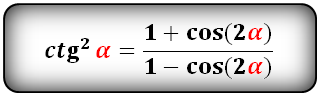
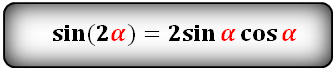
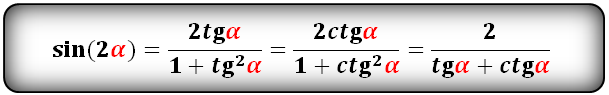
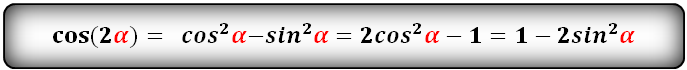
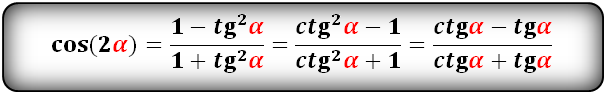
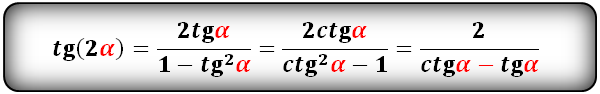
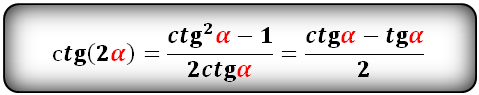


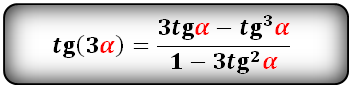
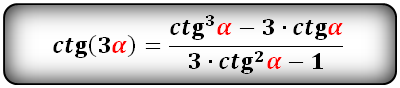


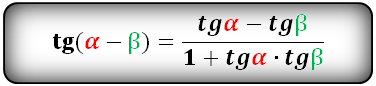
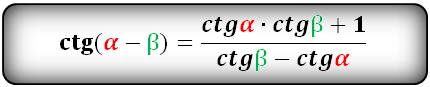
 Игроки могут получить их из внутриигровых событий, наград за прохождение основного сюжета и путем покупки в магазине.
Игроки могут получить их из внутриигровых событий, наград за прохождение основного сюжета и путем покупки в магазине.


 Для функции периода y = A cos (Bx + C) ее амплитуда равна A. Период T = 2 pi/B и фазовый сдвиг равен C.
Для функции периода y = A cos (Bx + C) ее амплитуда равна A. Период T = 2 pi/B и фазовый сдвиг равен C. 
