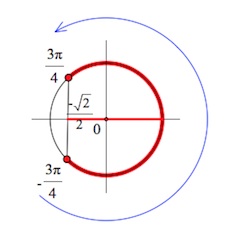
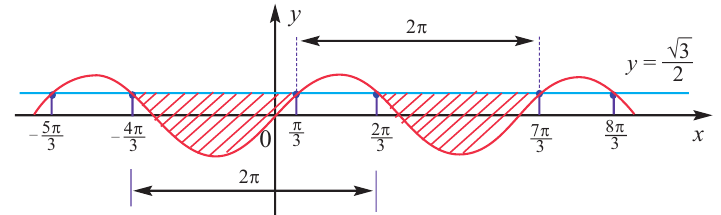
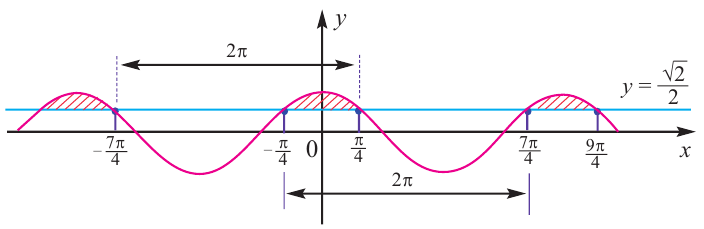
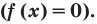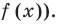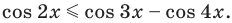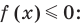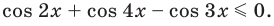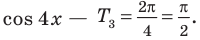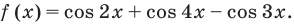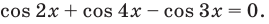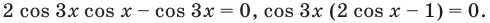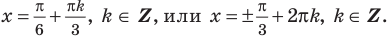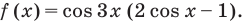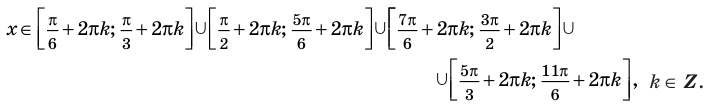Согласно неравенству, нам нужны значения синуса больше либо равные (-frac{sqrt{2}}{2}), на рисунке показали их при помощи синей штриховки. Этим значениям соответствуют углы, лежащие на дуге (MN), включая точки (M) и (N). Дугу (MN) с нужными углами можно записать в виде промежутка ПРОТИВ часовой стрелки. То есть от точки (M) к (N). Получается такой промежуток:
$$x in [-frac{pi}{4}+2pi*n; -frac{3pi}{4}+2pi*n], quad n in Z;$$
Скобки квадратные так как знак неравенства нестрогий и не забываем про период (2pi*n). Но сам промежуток неправильный!
Внимание! Так записывать ответ нельзя, потому что промежуток всегда должен быть от меньшего числа к большему. У нас это правило не соблюдается:
$$-frac{pi}{4}>-frac{3pi}{4};$$
Чтобы ответ был в правильном виде, достаточно просто прибавить к правой границе промежутка (2pi).
$$x in [-frac{pi}{4}+2pi*n; -frac{3pi}{4}+2pi+2pi*n], quad n in Z;$$
Приведем подобные слагаемые:
$$x in [-frac{pi}{4}+2pi*n; frac{5pi}{4}+2pi*n], quad n in Z;$$
Левая граница меньше правой, значит можно записывать ответ.
Ответ: (x in [-frac{pi}{4}+2pi*n; frac{5pi}{4}+2pi*n], quad n in Z).
Рассмотрим неравенство с синусом, которое наиболее часто встречается при нахождении ОДЗ.
Пример 3
$$sin(x)>0;$$
Решение аналогично предыдущим примерам. Рисуем единичную окружность, отмечаем на оси синусов значение (0), оно находится в начале координат. Углы на окружности, синус от которых будет равен (0) находятся в точках (A) и (C): это углы (0+2pi*n) и (pi+2pi*n). Все значения синуса выше (0) нас устраивают, соответствующие им углы лежат на дуге (AC), от точки (A) до (C).
08
Фев 2014
Категория: Справочные материалыТригонометрические выражения, уравнения и неравенства
Простейшие тригонометрические неравенства
2014-02-08
2015-04-20
Часть 1.
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков
,
.
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие
– левее точки
на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до
.
Обратите внимание, многие, назвав первую точку вместо второй точки
указывают точку
, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные
– правее точки
, включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что
.
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные
– выше точки
, включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:
Пример 4.
Решить неравенство:
Решение:
Кратко:
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению
, так как область значений функции
–
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
Если не очень понятно, загляните сюда –>+ показать
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
Автор: egeMax |
комментариев 179
Печать страницы
- Решение неравенств с синусом
- Решение неравенств с косинусом
- Решение неравенств с тангенсом
- Решение неравенств с котангенсом
- Примеры
п.1. Решение неравенств с синусом
Алгоритм решения неравенства (sinxgt a)
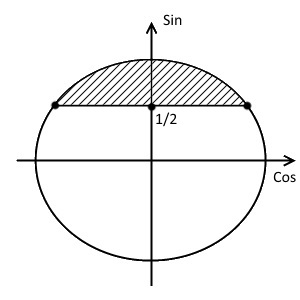
Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой (a). Провести горизонталь (y=a), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение (sinx=a). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((arcsina+2pi k; pi-arcsin a+2pi k))
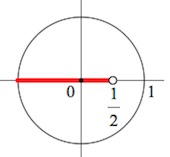
Например:
 |
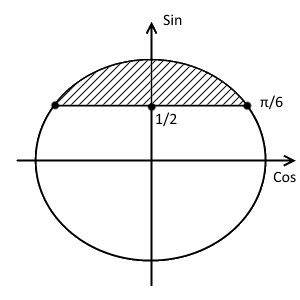
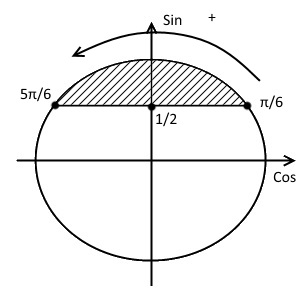
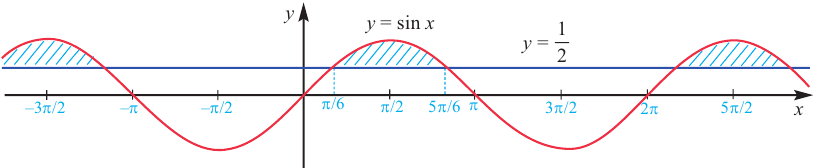
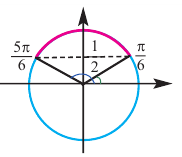
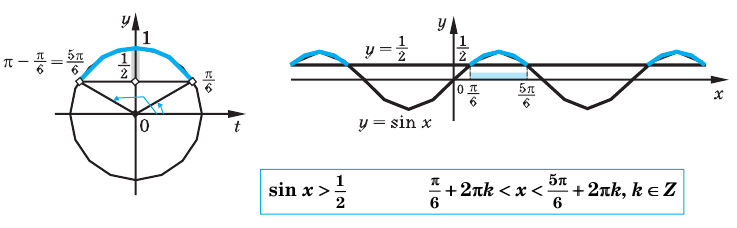
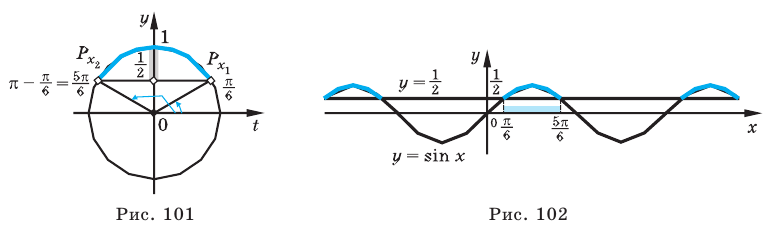
$$ sin xgt frac12 $$ 1. Проводим горизонталь (y=frac12), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (sinx=frac12) begin{gather*} x=(-1)^kfracpi6+pi k= left[ begin{array}{l l} fracpi6+2pi k\ frac{5pi}{6}+2pi k end{array} right. end{gather*} Подписываем точку справа (fracpi6) и точку слева (frac{5pi}{6}). 3. При обходе полученной дуги против часовой стрелки получаем интервал: ((fracpi6; frac{5pi}{6})). Добавляем к концам интервала полный период. Ответ: (left(fracpi6;+2pi k; frac{5pi}{6}+2pi kright)) |
Алгоритм решения неравенства (sinxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства (sinxlt a) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью (y=a). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).
Наконец, в неравенстве (sinxleq a) всё будет то же, что и в (sinxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
Например:
 |
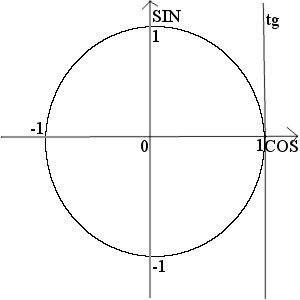
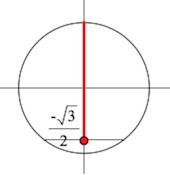
$$ sin xleq -frac{sqrt{2}}{2} $$ 1. Проводим горизонталь (y=-frac{sqrt{2}}{2}), отмечаем точки пересечения (закрашенные, т.к. неравенство нестрогое). 2. Решаем уравнение (sinx=-frac{sqrt{2}}{2}) begin{gather*} x=(-1)^kleft(-fracpi4right)+pi k= left[ begin{array}{l l} -frac{3pi}{4}+2pi k\ -frac{pi}{4}+2pi k end{array} right. end{gather*} Подписываем точку справа (-frac{3pi}{4}) и точку слева (-frac{pi}{4}). 3. При обходе полученной дуги против часовой стрелки получаем отрезок: (left[-frac{3pi}{4};-frac{pi}{4}right]). Добавляем к концам отрезка полный период. Ответ: (left[-frac{3pi}{4}+2pi k;-frac{pi}{4}+2pi kright]) |
п.2. Решение неравенств с косинусом
Алгоритм решения неравенства (cosxgt a)
Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой (a). Провести вертикаль (x=a), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение (cosx=a). Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((-arccosa+2pi k; arccosa+2pi k))
Например:
 |
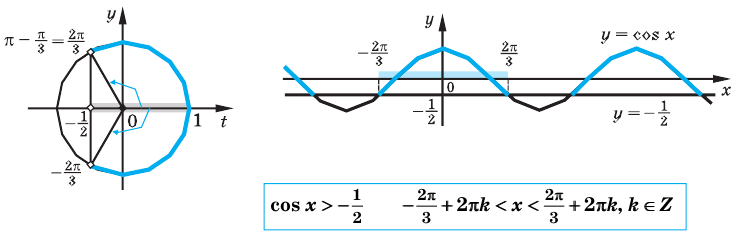
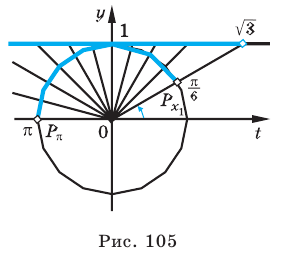
$$ cosxgt frac{sqrt{3}}{2} $$ 1. Проводим вертикаль (x=frac{sqrt{3}}{2}), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение (cosx=frac{sqrt{3}}{2}) begin{gather*} x=pmfracpi6+2pi k end{gather*} Подписываем точку снизу (-fracpi6) и точку сверху (frac{pi}{6}). 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi6right)). Добавляем к концам интервала полный период. Ответ: (left(-fracpi6;+2pi k; frac{pi}{6}+2pi kright)) |
Алгоритм решения неравенства (cosxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства (cosxlt a) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали (x=a). При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.
Наконец, в неравенстве (cosxleq a) всё будет то же, что и в (cosxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
п.3. Решение неравенств с тангенсом
Алгоритм решения неравенства (tgxgt a)
Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой (a). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.
Шаг 2. Решить уравнение (tgx=a). Полученное базовое решение является значением точки пересечения.
Шаг 3. Дуга числовой окружности от отмеченной точки до (fracpi2) (в которой (tgxrightarrow +infty)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: (left(arctga+pi k; fracpi2+pi kright))
Например:
 |
$$ tg xgt -frac{1}{sqrt{3}} $$ 1. На оси тангенсов отмечаем точку (-frac{1}{sqrt{3}}). Проводим луч из начала координат через эту точку. 2. Решаем уравнение (tgx=-frac{1}{sqrt{3}}) begin{gather*} x=-fracpi6+pi k end{gather*} Подписываем точку снизу (-fracpi6.) Верхней границей интервала будет (fracpi2), угол, в котором (tgxrightarrow +infty .) 3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi2right)). Добавляем к концам интервала период для тангенса. Строго говоря, на числовой окружности длиной (2pi) получим две дуги для тангенса с периодом (pi). Ответ: (left(-fracpi6;+pi k; frac{pi}{2}+pi kright)) |
Алгоритм решения неравенства (tgxlt a) будет отличаться тем, что в ответе нужно записывать дугу от точки (-fracpi2) (в которой (tgxrightarrow -infty)) до найденного арктангенса.
Для нестрогих неравенств будут получаться полуинтервалы, в которых точки (pmfracpi2) ((tgxrightarrow pminfty)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.
п.4. Решение неравенств с котангенсом
Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).
В неравенствах вида (ctgxgt a) пределу (ctgxrightarrow +infty) соответствует угол 0.
В неравенствах вида (ctgxlt a) пределу (ctgxrightarrow -infty) соответствует угол (pi).
п.5. Примеры
Пример 1. Решите неравенства:
Пример 2*. Решите неравенства:
 |
a) (cosxgt -1) Справа от вертикали (x=-1) расположена вся числовая окружность, кроме точки (pi). Ответ: (xne pi+2pi k) |
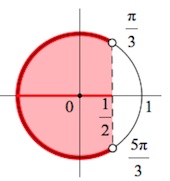
 |
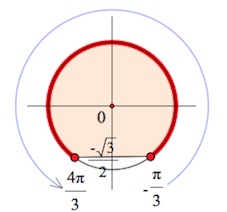
б) (4cos^2frac x2-3leq 0) (4cdot frac{1+cosx}{2}leq 3) (2+2cosxleq 3) (cosxleqfrac12) Ответ: (left[fracpi3+2pi k; frac{5pi}{3}+2pi kright]) |
в) (-sqrt{3}lt tgxleq 5)
(-arctgsqrt{3}+pi klt xleq arctg5+pi k)
(-fracpi3+pi klt xleq arctg5+pi k)
Ответ: (left.left(-frac{pi}{3}+pi k; arctg5+pi kright.right])
г) (tgleft(x-fracpi4right)gtsqrt{3})
(arctgsqrt{3}+pi klt x-fracpi4ltfracpi2+pi k)
(fracpi4+fracpi3+pi klt xltfracpi4+fracpi2+pi k)
(frac{7pi}{12}+pi klt xltfrac{3pi}{4}+pi k)
Ответ: (left(frac{7pi}{12}+pi k; frac{3pi}{4}+pi kright))
Содержание:
Для решение простейших тригонометрических неравенств можно использовать как единичную окружность, так и графики тригонометрических функций.
Пример 1.
Решим неравенство
Решение:
Запишем решение в общем виде.
Решить данное неравенство значит, найти абсциссы множества точек графика функции 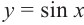
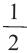
1.Построим график функции 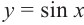
2.В одной системе координат построим график функции 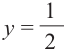
3.Отметим точки пересечения графиков.
4. Как видно, прямая 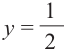
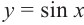
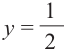
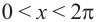
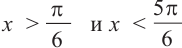
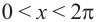
Также решения тригонометрических неравенств можно ясно увидеть на единичной окружности. Все остальные интервалы, удовлетворяющие решению неравенства получаются смещением интервала 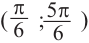
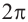
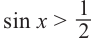
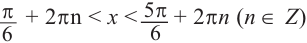
Пример 2.
Решим неравенство
Решение:
Решения уравнения 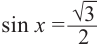
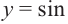
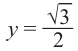
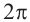
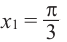
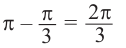
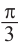
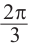
От каждой из них, по обе стороны, отметим ещё две точки — вправо от
точки 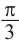
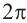
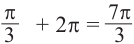
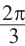
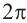
Они также являются абсциссами точек пересечения графиков.
На промежутке (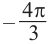
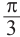
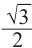
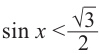
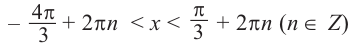
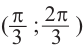
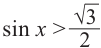
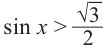
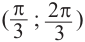
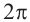
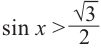
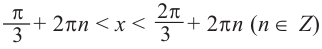
Пример 3.
Решим неравенство
Решение:
Найдём абсциссы точек пересечения графиков функций
и 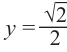
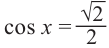
Получим: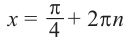
При 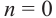
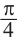
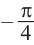
Отметим от точки 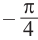
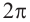
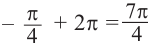
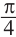
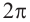
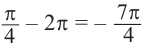
Один из промежутков, удовлетворяющих неравенству, расположен между наименьших но абсолютному значению корней соответствующего уравнения, т.е. между точками 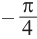
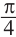
Приняв во внимание периодичность 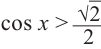
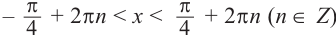
По графику решение неравенства 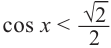
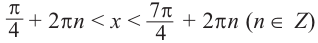
Пример 4.
Решим неравенства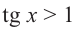
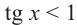
Решение:
В одной системе координат построим графики функций 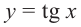
Найдём абсциссу точки пересечения , расположенной в интервале 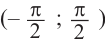
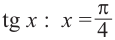
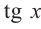
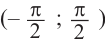
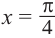
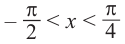
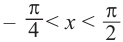
Так как функция 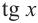
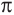
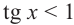
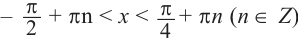
tg х > 1 будет 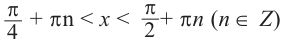
Пример 5.
Решим неравенства 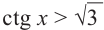
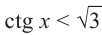
Решение:
На одной координатной плоскости построим графики функций 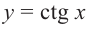
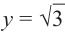
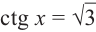
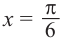
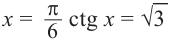
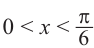
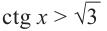
если 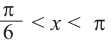
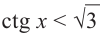
Это говорит о том , что условию неравенства 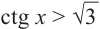
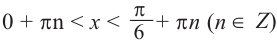
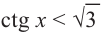
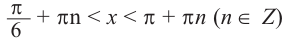
Для решения тригонометрических неравенств:
1) В одной системе координат постройте графики функций из левой и правой частей неравенства;
2) Решите соответствующие уравнения. Найдите абсциссы для нескольких точек пересечения, расположенных близко к началу координат и отметьте их на графике;
3) Определите какой-либо интервал, удовлетворяющий неравенству;
4) Принимая во внимание периодичность функции, запишите все решения.
Пример 6.
Решите неравенство 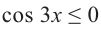
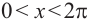
Решение:
1.Построим график функции 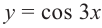
Как видно из графика, значения 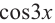
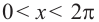
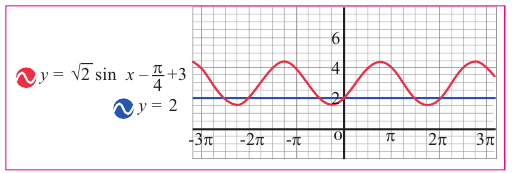
Пример 7.
Решим неравенство 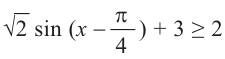
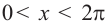
Решение:
1. Построим графики функций 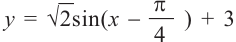
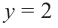
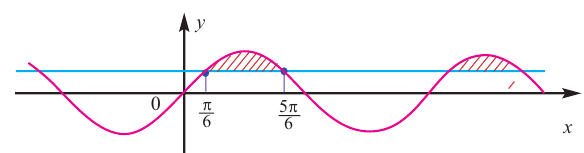
Решением неравенства являются абсциссы всех точек, которые расположены на прямой у = 2 и выше неё. Это точки 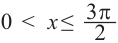
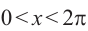
А общее решение неравенства имеет вид 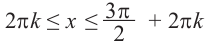
Проверка: На интервале решения для проверки выберем одну точку, напри-л
мер 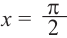
Пример 8.
Решение:
Пусть 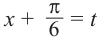
Пример решении задачи:
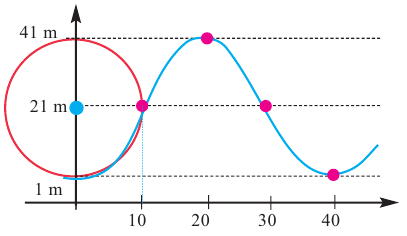
Карусель, радиусом 20 м за каждые 40 секунд совершает один оборот. Самое низкое сиденье находится на высоте 1 м.
а)Изобразите график, соответствующий задаче.
б)Запишите функцию зависимости движения человека, находящегося на сиденье карусели в виде 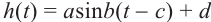
в)В какие секунды за один полный оборот человек на карусели, окажется на высоте выше 21 м?
Решение:
а) Изобразим схематично решение задачи. Отметим на окружности точки, соответствующие каждой четвёртой части оборота при движении карусели. Соединим эти точки и получим график, в виде синусоиды, движения карусели за один оборот (360°).
б)Из графика видно, что с 10 но 30 секунду человек на карусели, будет находится на высоте от 21 ми более.
в)По данным задачи и графику запишем формулу функции.
Зная период, найдём частоту b:
Найдём амплитуду и среднюю линию, зная максимальное и минимальное значения. 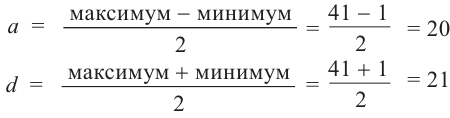
Формула имеет вид 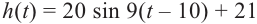
Решение неравенств
Понятия неравенства с одной переменной и его способы решения:
Определение:
Если два выражения с переменной соединить одним из знаков 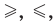
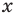
Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
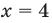
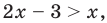
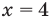
Область допустимых значений (ОДЗ):
Областью допустимых значений (или областью определения) неравенства называется общая область определения для функций 
Для неравенства 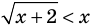
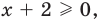
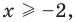
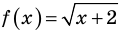
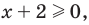
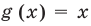
Два неравенства называется равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго и наоборот, каждое решение второго неравенства является решением первого.
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не меняя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное задан ному (на ОДЗ заданного неравенства).
- Метод интервалов (решения неравенств вида
Решите неравенство
Пусть
ОДЗ:
Нули функции
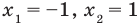
Ответ:
Схема поиска плана решения неравенства
Объяснение и обоснование:
Понятия неравенства с переменной и его решение
Если два выражения с переменной соединить одним из знаков 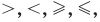
Аналогично уравнению, неравенство с переменной (например, со знаком 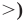
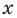
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
Например, решениями неравенства 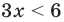
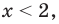

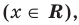
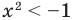
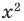
Область допустимых значений (ОДЗ) неравенства
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство 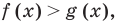
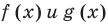
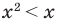
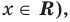
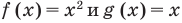
Понятно, что каждое решение заданного неравенства входит как в область определения функции 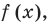
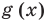
Например, в неравенстве 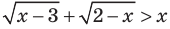
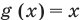
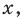
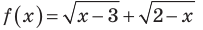
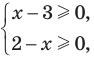
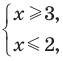
В основном при решении неравенств различных видов приходится применять один из двух методов решения: равносильные преобразования неравенств или так называемый метод интервалов.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго, и наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. Укажем, что в том случае, когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, а и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны (соответствующие ориентиры схематически представлены в пункте 5 табл. 38).
Например, чтобы решить с помощью равносильных преобразований неравенство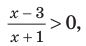
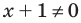
Решение:
Данное неравенство равносильно совокупности двух систем:
Тогда получаем
Таким образом,
Ответ:
Комментарий:
Заметим, что при записи условия положительности дроби — совокупности систем (2) — мы неявно учли ОДЗ неравенства (1). Действительно, если 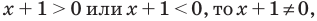
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок 
Метод интервалов
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функции. Объясним эти свойства, используя графики известных нам функций, например функций 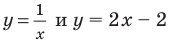
Рассматривая эти графики, замечаем, что функция может изменить свой знак только в двух случаях:
- если график разрывается (как в случае функции
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
- если график без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот). Но тогда график пересекает ось
(как в случае функции
(рис. 100,6).
На оси 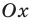
Точки, в которых разрывается график функции 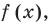
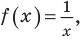
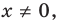
В таблице 39 приведено решение дробно-рационального неравенства 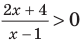
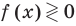
Пример №1
Решение:
1. ОДЗ: 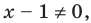
Рассмотрим функцию, стоящую в левой части этого неравенства, и обозначим ее через 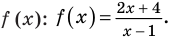
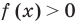
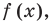
1. Найти ОДЗ неравенства.
2. Нули
тогда
Нас интересуют те промежутки области определения функции 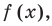
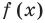
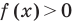
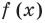
2. Найти нули
Если теперь отметить нули на области определения функции 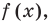
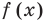
3. Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ.
4 Ответ:
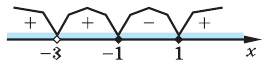
Из рисунка видно, что решением неравенства является объединение промежутков
4. Записать ответ, учитывая знак неравенства.
Приведем пример решения более сложного дробно-рационального неравенства методом интервалов и с помощью равносильных преобразований.
Пример №2
Решите неравенство
1 способ (метод интервалов)
Решение:
Пусть
1 ОДЗ:
2. Нули
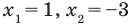
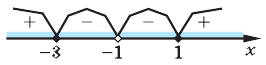
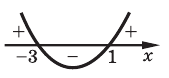
3. Отмечаем нули функции на ОДЗ и находим знак 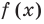
Ответ:
Комментарий:
Данное неравенство имеет вид 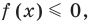
При нахождении нулей 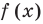
Записывая ответ к нестрогому неравенству, следует учесть, что все нули функции должны войти в ответ (в данном случае — числа -3 и 1).
2 способ (с помощью равносильных преобразований)
Комментарий:
Выберем для решения метод равносильных преобразований неравенства. При выполнении равносильных преобразований мы должны учесть ОДЗ данного неравенства, то есть учесть ограничение
Но если 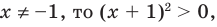
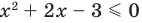
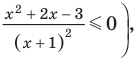
Чтобы решить полученное квадратное неравенство, найдем корни квадратного трехчлена 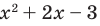
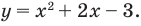
Поскольку все преобразования были равносильными только на ОДЗ, то мы должны выбрать те решения квадратного неравенства, которые удовлетворяют ограничению ОДЗ.
Решение:
ОДЗ:
Тогда 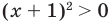
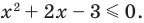
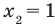
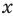
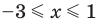
Учитывая ОДЗ, получаем ответ.
Ответ:
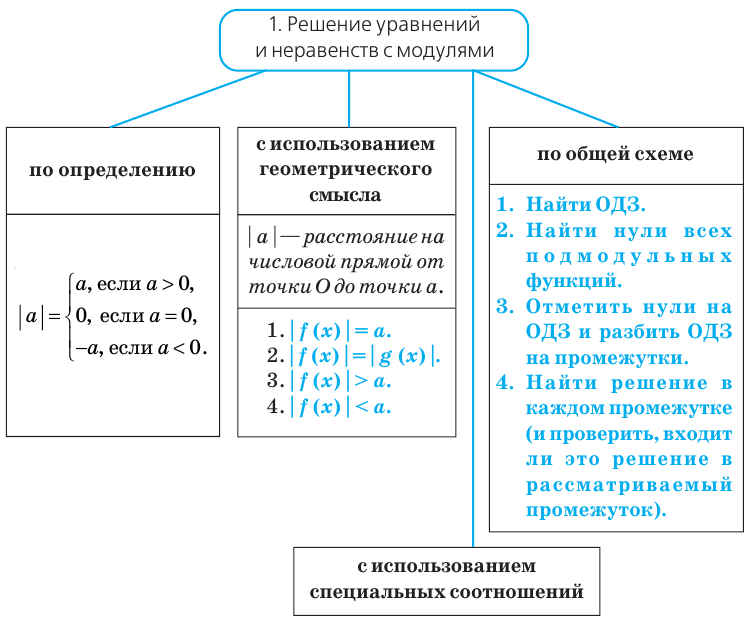
Уравнения и неравенства с модулями
Использование геометрического смысла модуля ( при
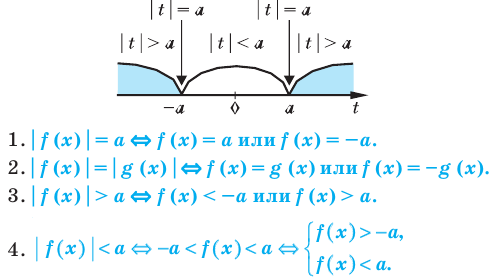
Обобщение:
Использование специальных соотношений:
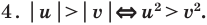
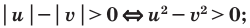
Объяснение и обоснование:
Решение любых уравнений или неравенств с модулем
Решать любое уравнение или неравенство с модулем можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений (табл. 40).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №3
Решите уравнение
1 способ (по определению модуля)
Решение:
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (1).
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (2).
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая: 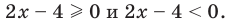
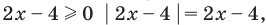
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
2 способ (использование геометрического смысла модуля)
Решение:
Ответ: 5; -1.
Комментарий:
С геометрической точки зрения 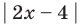
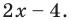
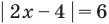
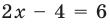
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств с модулями — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции 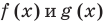
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции 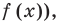
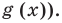
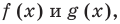
Чтобы продолжить решение неравенств 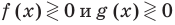
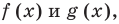
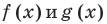
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
Примеры решения задач:
Пример №4
Решите уравнение
Решение:
1. ОДЗ:
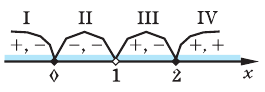
2. Нули подмодульных функций:
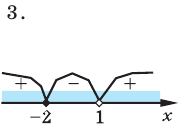
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные функции имеют знаки*, показанные на рисунке.
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках 1 и 3, удобно для решения объединить эти промежутки).
Промежутки 1 и 3 : 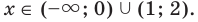
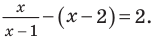
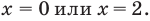
Промежуток 2: 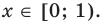
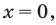
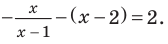
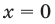
Промежуток 4: 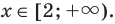
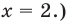
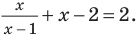
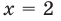
Ответ: 0; 2.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 40. Обоснуем, например, соотношение
Запишем заданное равенство в виде 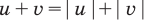
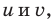
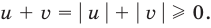
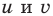
неотрицательные. Наоборот, если 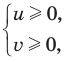
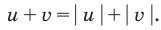
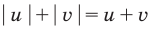
- Заказать решение задач по высшей математике
Пример №5
Решите уравнение
Решение:
Поскольку 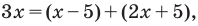
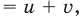
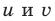
Таким образом,
Ответ:
Комментарий:
Если обозначить 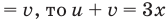
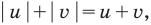
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким но системе
При решении неравенств с модулями рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений с модулями.
Пример №6
Решите неравенство
Решение:
Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству 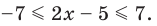
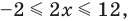
Ответ:
Комментарий:
Неравенство вида 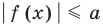
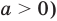
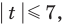
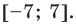
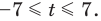
Пример №7
Решите неравенство
Решение:
1. ОДЗ: 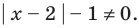
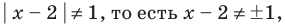
2. Нули подмодульных функций: 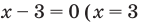
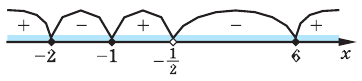
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке (на каждом из промежутков первый знак — это знак функции 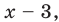
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 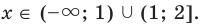
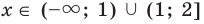
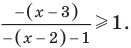
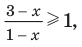
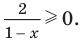
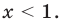
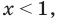
Промежуток III: 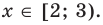
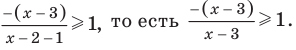
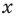
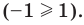
Промежуток IV: 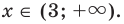
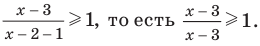
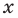
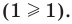
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ:
Ответ:
Укажем, что для решения некоторых неравенств с модулями удобно применять также специальные соотношения, приведенные в таблице 40.
Пример №8
Решите неравенство
Решение:
Поскольку 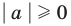
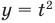
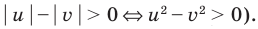
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов (см. рисунок)получаем
Ответ:
Общая схема, предложенная в таблице 40, может быть использована не только при решении уравнений или неравенств с модулями, но и при выполнении преобразований выражений с модулями.
Например, для построения графика функции 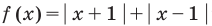
Оформление решения подобного примера может быть таким.
Пример №9
Постройте график функции
Решение:
1. Область определения функции:
2. Нули подмодульных функций:
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке также указаны знаки подмодульных функций в каждом из промежутков). 4. Тогда
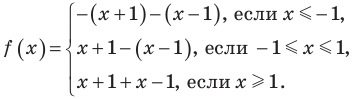
Строим график этой функции (см. рисунок).
Решение тригонометрических неравенств
Примеры решения простейших тригонометрических неравенств:
Способы решения более сложных тригонометрических неравенств:
а) Использование равносильных преобразований и, в частности, сведение тригонометрического неравенства к алгебраичкому неравенству по схеме: 1) к одному аргументу, 2) к одной функции, 3) замена переменной (аналогично схеме решения тригонометрических уравнений, приведенной на с. 170) и последующее решение полученных простейших тригонометрических неравенств.
б) Использование метода интервалов (после сведения неравенства к виду 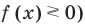
- Найти ОДЗ неравенства.
- Найти общий период (если он существует) для всех функций, входящих в неравенство, то есть период функции
- Найти нули функции:
- Отметить нули функции на ОДЗ на одном периоде и найти знак функции
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
- Записать ответ, учитывая знак заданного неравенства и период функции
Объяснение и обоснование:
Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами считают неравенства вида 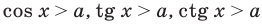
Чтобы рассуждения по нахождению решений этих неравенств были более наглядными, используют единичную окружность или графики соответствующих функций, как это показано в первом пункте таблицы 41.
Пример №10
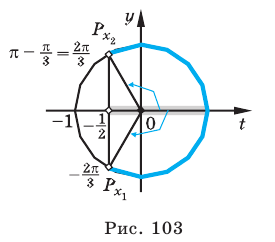
Объясним более детально решение неравенства 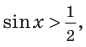
Решение:
Поскольку 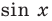
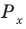
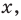
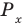
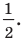
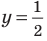
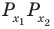
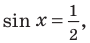
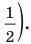
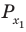
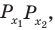
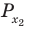
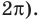
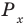
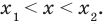
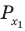
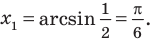
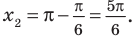
Через период 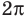
Ответ:
Для решения неравенства 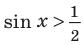
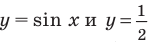
Решениями неравенства 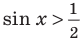
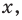
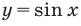
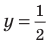
Достаточно решить уравнение 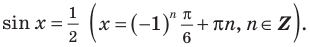
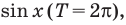
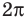
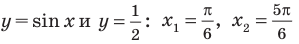
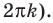
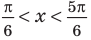
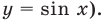
Ответ:
Аналогично можно получить и решения других видов простейших неравенств, приведенных в пункте 1 таблицы 41.
Пример №11
Решите неравенство
Решение:
Поскольку 
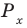
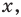
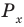
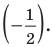
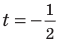
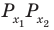
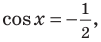
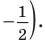
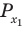
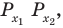
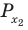
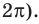
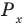
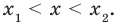
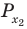
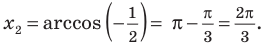
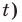
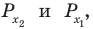
Таким образом, на одном 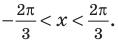
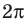
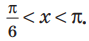
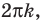
Ответ:
Рассуждения при использовании графической иллюстрации решения неравенства 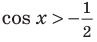
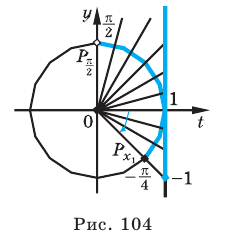
Пример №12
Решите неравенство
Решение:
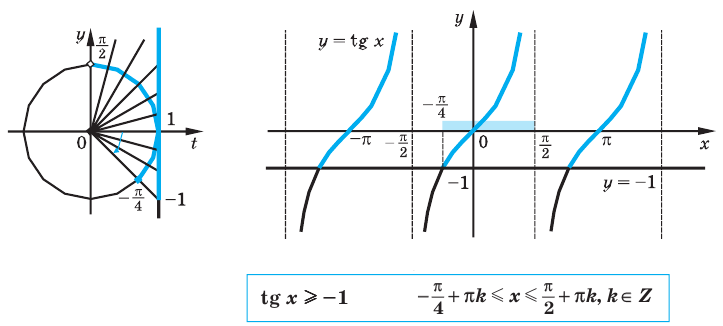
Период тангенса равен 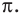
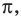
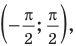
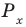
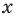
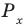
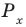
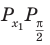
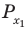
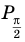
Поскольку точка 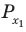
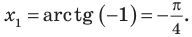
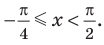
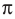
Ответ:
Заметим, что при решении данного неравенства с использованием графиков достаточно, как и в предыдущих случаях, на одном периоде (например, на промежутке 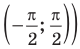
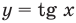
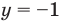
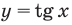
Пример №13
Решите неравенство
Решение:
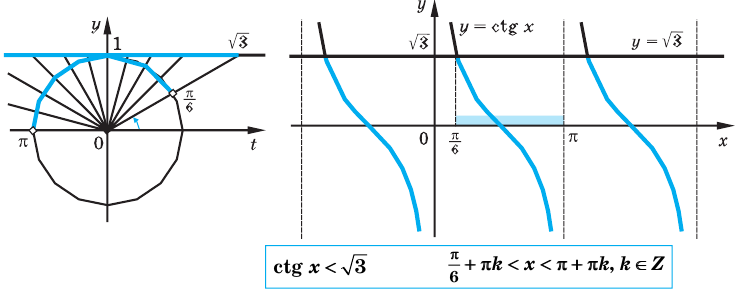
Период котангенса равен 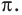
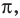
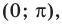
Сначала выделим на линии котангенсов значения котангенсов, меньшие, чем 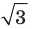
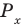
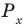
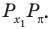
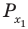
Таким образом, на одном периоде решениями данного неравенства являются
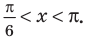
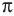
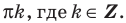
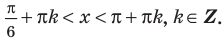
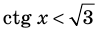
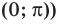
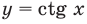
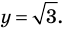
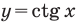
Способы решения более сложных тригонометрических неравенств
Способы решения более сложных тригонометрических неравенств также проиллюстрируем на примерах.
Пример №14
Решите неравенство:
Решение:
Тогда 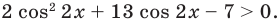
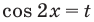
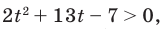
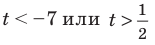
Обратная замена дает: 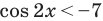
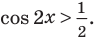
Таким образом,
Комментарий:
Используем равносильные преобразования данного неравенства. Для этого приведем его к алгебраическому по схеме, аналогичной схеме решения
- к одному аргументу
- к одной функции
- проведем замену переменной
После обратной замены решим полученные простейшие тригонометрические неравенства.
Решая более сложные тригонометрические неравенства, можно также применить метод интервалов, немного изменив его. Необходимость коррекции известной схемы решения неравенств 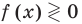
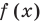
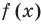
Таким образом, метод интервалов для решения тригонометрических неравенств 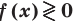
- Найти ОДЗ неравенства.
- Найти период функции
(если он существует).
- Найти нули функции
- Отметить нули на ОДЗ внутри одного периода и найти знак функции в каждом из промежутков, на которые разбивается ОДЗ (внутри одного периода).
- Записать ответ (учитывая знак заданного неравенства и период функции
Пример №15
Решите неравенство
Решение:
Решим данное неравенство методом интервалов. Для этого приведем его к виду
1. ОДЗ: 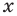
2. Как мы знаем, период функции 
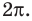
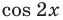
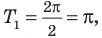
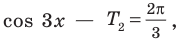
На отрезке длиной 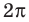
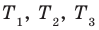
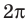
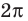
3.Найдем нули этой функции:
Тогда
Отсюда 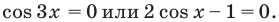
4. Отметим все нули на периоде длиной 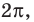
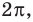
Находим знаки функции 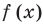
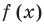
Ответ (записывается с учетом периода):
Замечание. При решении тригонометрических неравенств методом интервалов часто приходится находить знак функции в большом количестве промежутков. Для того чтобы уменьшить объем работы, можно предложить такой способ: следить за тем, через какой нуль мы проходим при переходе от одного интервала к другому и изменяется ли знак заданной функции в этом нуле.
В случае, когда функция 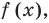
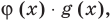
Практически для использования этого свойства в случае, если левая часть неравенства записана как произведение нескольких функций, нули каждого множителя отмечают на промежутке разным цветом (так, как это сделано на рисунке к задаче 6), или, если множителей только два, нули первого множителя обозначают под осью, а нули второго — над осью.
Если у функций-множителей нет одинаковых нулей, то знак функции 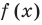
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
Большинство студентов тригонометрические неравенства недолюбливают. А зря. Как говаривал один персонаж,
«Вы просто не умеете их готовить»
Так как же «готовить» и с чем подавать неравенство с синусом мы разберёмся в этой статье. Решать мы будем самым простым способом — с помощью единичной окружности.
Итак, перво-наперво нам потребуется следующий алгоритм.
Алгоритм решения неравенств с синусом:
- на оси синуса откладываем число $a$ и проводим прямую параллельно оси косинусов до пересечения с окружностью;
- точки пересечения этой прямой с окружностью будут закрашенными, если неравенство нестрогое, и не закрашенными, если неравенство строгое;
- область решения неравенства будет находится выше прямой и до окружности, если неравенство содержит знак «$>$», и ниже прямой и до окружности, если неравенство содержит знак «$<$»;
- для нахождения точек пересечения, решаем тригонометрическое уравнение $sin{x}=a$, получаем $x=(-1)^{n}arcsin{a} + pi n$;
- полагая $n=0$, мы находим первую точку пересечения (она находится или в первой, или в четвёртой четверти);
- для нахождения второй точки, смотрим, в каком направлении мы идём по области ко второй точке пересечения: если в положительном направлении, то следует брать $n=1$, а, если в отрицательном, то $n=-1$;
- в ответ выписывается промежуток от меньшей точки пересечения $+ 2pi n$ до большей $+ 2pi n$.
Ограничение алгоритма
Важно: данный алгоритм не работает для неравенств вида $sin{x} > 1; sin{x} geq 1, sin{x} < -1, sin{x} leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом — решение сводится к решению уравнения $sin{x} = 1$ или $sin{x} = -1$.
Частные случаи при решении неравенства с синусом
Важно отметить также следующие случаи, которые гораздо удобнее решить логически, не используя вышеуказанный алгоритм.
Частный случай 1. Решить неравенство:
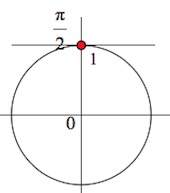
$sin{x} leq 1.$
В силу того, что область значения тригонометрической функции $y=sin{x}$ не больше по модулю $1$, то левая часть неравенства при любом $x$ из области определения (а область определения синуса — все действительные числа) не больше $1$. А, значит, в ответ мы записываем: $x in R$.
Следствие: аналогично решается и неравенство
$sin{x} geq -1.$
Частный случай 2. Решить неравенство:
$sin{x} < 1.$
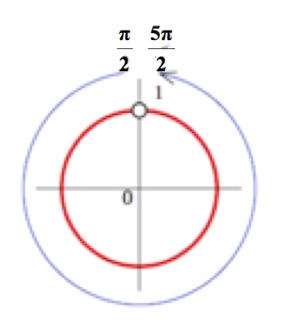
Применяя аналогичные частному случаю 1 рассуждения, получим, что левая часть неравенства меньше $1$ для всех $x in R$, кроме точек, являющихся решением уравнения $sin{x} = 1$. Решая это уравнение, будем иметь:
$x = (-1)^{n}arcsin{1}+ pi n = (-1)^{n}frac{pi}{2} + pi n.$
А, значит, в ответ мы записываем: $x in R backslash left{(-1)^{n}frac{pi}{2} + pi nright}$.
Следствие: аналогично решается и неравенство
$sin{x} > -1.$
Примеры решения неравенств с помощью алгоритма.
Пример 1: Решить неравенство:
$sin{x} geq frac{1}{2}.$
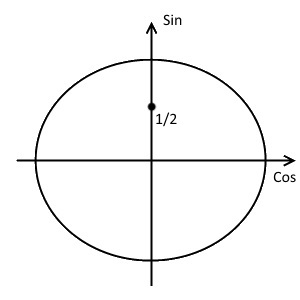
- Отметим на оси синусов координату $frac{1}{2}$.
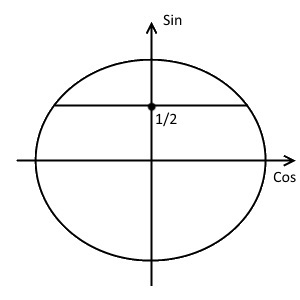
- Проведём прямую параллельно оси косинусов и проходящую через эту точку.
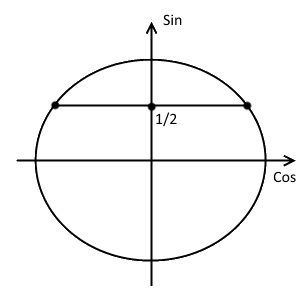
- Отметим точки пересечения. Они будут закрашенными, так как неравенство нестрогое.
- Знак неравенства $geq$, а значит закрашиваем область выше прямой, т.е. меньший полукруг.
- Находим первую точку пересечения. Для этого неравенство превращаем в равенство и решаем его: $sin{x}=frac{1}{2} Rightarrow x=(-1)^{n}arcsin{frac{1}{2}}+pi n =(-1)^{n}frac{pi}{6} + pi n$. Полагаем далее $n=0$ и находим первую точку пересечения: $x_{1}=frac{pi}{6}$.
- Находим вторую точку. Наша область идёт в положительном направлении от первой точки, значит $n$ полагаем равным $1$: $x_{2}=(-1)^{1}frac{pi}{6} + pi cdot 1 = pi — frac{pi}{6} = frac{5pi}{6}$.
Таким образом, решение примет вид:
$x in left[frac{pi}{6} + 2pi n; frac{5pi}{6} + 2 pi nright], n in Z.$
Пример 2: Решить неравенство:
$sin{x} < -frac{1}{2}$
Отметим на оси синусов координату $- frac{1}{2}$ и проведём прямую параллельно оси косинусов и проходящую через эту точку. Отметим точки пересечения. Они будут не закрашенными, так как неравенство строгое. Знак неравенства $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:
$sin{x}=-frac{1}{2}$
$x=(-1)^{n}arcsin{left(-frac{1}{2}right)}+ pi n =(-1)^{n+1}frac{pi}{6} + pi n$.
Полагая далее $n=0$, находим первую точку пересечения: $x_{1}=-frac{pi}{6}$. Наша область идёт в отрицательном направлении от первой точки, значит $n$ полагаем равным $-1$: $x_{2}=(-1)^{-1+1}frac{pi}{6} + pi cdot (-1) = -pi + frac{pi}{6} = -frac{5pi}{6}$.
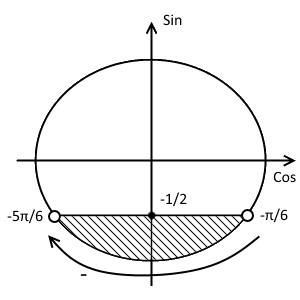
$x in left(-frac{5pi}{6} + 2pi n; -frac{pi}{6} + 2 pi nright), n in Z.$
Пример 3: Решить неравенство:
$1 — 2sin{left(frac{x}{4}+frac{pi}{6}right)} leq 0.$
Этот пример решать сразу с помощью алгоритма нельзя. Для начала его надо преобразовать. Делаем в точности так, как делали бы с уравнением, но не забываем про знак. Деление или умножение на отрицательное число меняет его на противоположный!
Итак, перенесём всё, что не содержит тригонометрическую функцию в правую часть. Получим:
$- 2sin{left(frac{x}{4}+frac{pi}{6}right)} leq -1.$
Разделим левую и правую часть на $-2$ (не забываем про знак!). Будем иметь:
$sin{left(frac{x}{4}+frac{pi}{6}right)} geq frac{1}{2}.$
Опять получилось неравенство, которое мы не можем решить с помощью алгоритма. Но здесь уже достаточно сделать замену переменной:
$t=frac{x}{4}+frac{pi}{6}.$
Получаем тригонометрическое неравенство, которое можно решить с помощью алгоритма:
$sin{t} geq frac{1}{2}.$
Это неравенство было решено в примере 1, поэтому позаимствуем оттуда ответ:
$t in left[frac{pi}{6} + 2pi n; frac{5pi}{6} + 2 pi nright].$
Однако, решение ещё не закончилось. Нам нужно вернуться к исходной переменной.
$(frac{x}{4}+frac{pi}{6}) in left[frac{pi}{6} + 2pi n; frac{5pi}{6} + 2 pi nright].$
Представим промежуток в виде системы:
$left{begin{array}{c} frac{x}{4}+frac{pi}{6} geq frac{pi}{6} + 2pi n, \ frac{x}{4}+frac{pi}{6} leq frac{5pi}{6} + 2 pi n. end{array} right.$
В левых частях системы стоит выражение ($frac{x}{4}+frac{pi}{6}$), которое принадлежит промежутку. За первое неравенство отвечает левая граница промежутка, а за второе — правая. Причём скобки играют немаловажную роль: если скобка квадратная, то неравенство будет нестрогим, а если круглая, то строгим. наша задача получить слева $x$ в обоих неравенствах.
Перенесём $frac{pi}{6}$ из левой части в правые, получим:
$left{begin{array}{c} frac{x}{4} geq frac{pi}{6} + 2pi n -frac{pi}{6}, \ frac{x}{4} leq frac{5pi}{6} + 2 pi n — frac{pi}{6}. end{array} right.$
Упрощая, будем иметь:
$left{begin{array}{c} frac{x}{4} geq 2pi n, \ frac{x}{4} leq frac{2pi}{3} + 2 pi n. end{array} right.$
Умножая левые и правые части на $4$, получим:
$left{begin{array}{c} x geq 8pi n, \ x leq frac{8pi}{3} + 8 pi n. end{array} right.$
Собирая систему в промежуток, получим ответ:
$x in left[ 8pi n; frac{8pi}{3} + 8 pi nright], n in Z.$



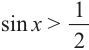
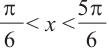
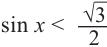
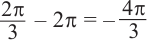
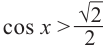
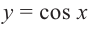
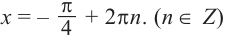
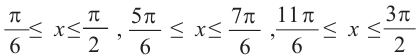
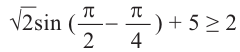
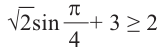
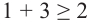
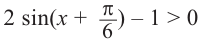
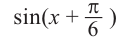
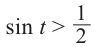
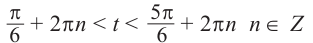
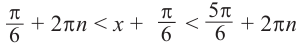
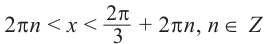


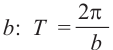
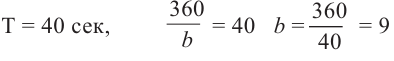
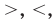
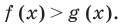
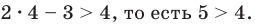
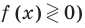
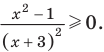
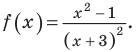
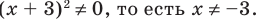
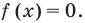
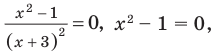

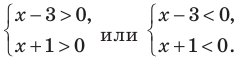
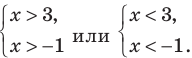
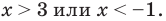
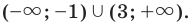
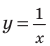 (рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);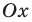 (как в случае функции
(как в случае функции 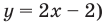 (рис. 100,6).
(рис. 100,6).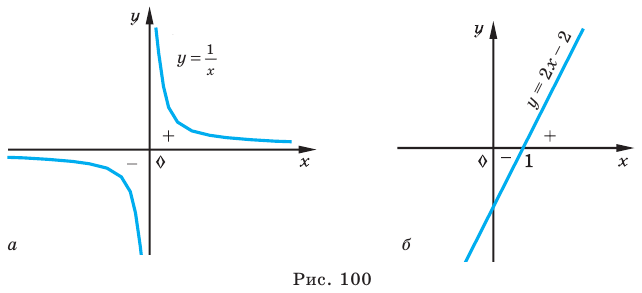
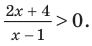
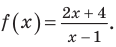
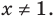
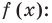
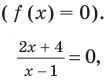
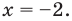
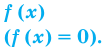
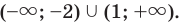

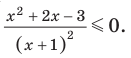
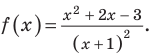
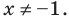
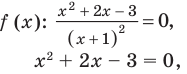
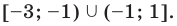
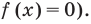
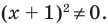
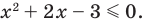
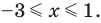
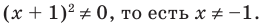
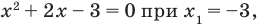
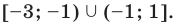
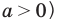
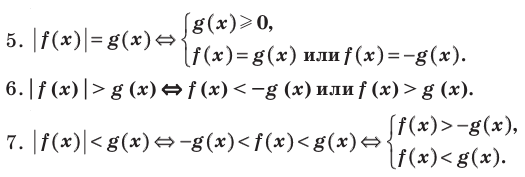
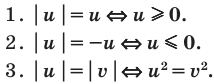
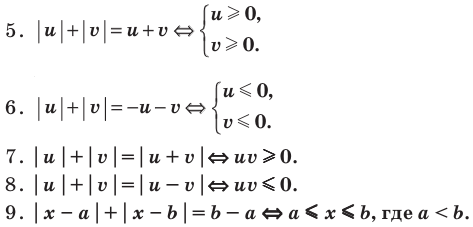
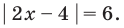
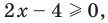 то получаем уравнение
то получаем уравнение 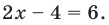 Тогда
Тогда 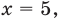 что удовлетворяет и условию (1).
что удовлетворяет и условию (1).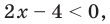 то получаем уравнение
то получаем уравнение 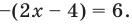 Тогда
Тогда 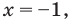 что удовлетворяет и условию (2).
что удовлетворяет и условию (2).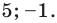
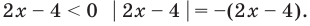
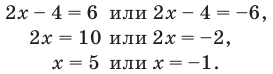
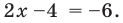
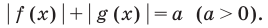
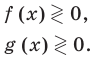
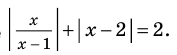
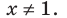
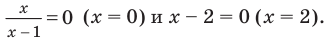
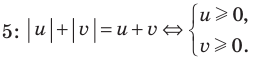
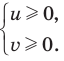
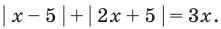
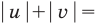
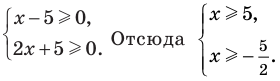
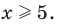
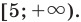
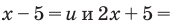
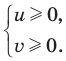
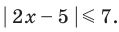
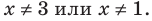
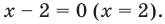
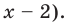
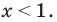
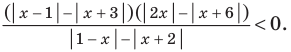
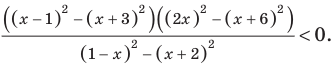
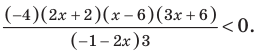
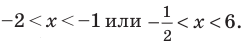
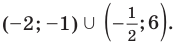
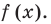
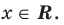

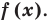
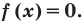
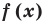 в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).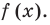
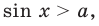

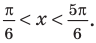
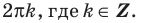
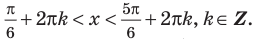
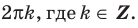
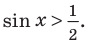
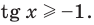
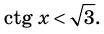
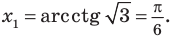
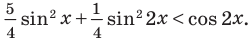
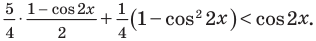
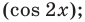
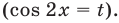 После обратной замены решим полученные простейшие тригонометрические неравенства.
После обратной замены решим полученные простейшие тригонометрические неравенства.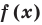 (если он существует).
(если он существует).