hell_yeah писал(а):
Это разве не 30 градусов будет?
Я имел ввиду без таблицы найти,а посчитать через радианы
Если калькуляторами и таблицами пользоваться нельзя, то есть два пути:
1) Перевести данный угол из радианной меры в градусную. Построить в прямоугольной системе координат окружность с центром в начале координат и радиусом, равным 1 (в качестве единичного отрезка можно взять, например, десять клеточек или 100 клеточек, если есть миллиметровка). Затем берёте точку [math]{P_0}left( {1;0} right)[/math] и поворачиваете её вокруг начала координат ( [math]Oleft( {0;0} right)[/math]) на угол [math]alpha[/math]. В результате получится новая точка единичной окружности [math]{P_alpha }left( {x;y} right)[/math]. Это точку можно построить с помощью транспортира. Так вот, первая координата точки [math]{P_alpha }[/math] — это и есть [math]cos alpha[/math], а вторая координата — это есть [math]sin alpha[/math], т.е. [math]cos alpha = x[/math], [math]sin alpha = y[/math]. Осталось только приближённо найти эти координаты. Для этого нужно опустить из точки [math]{P_alpha }[/math] перпендикуляры на оси [math]Ox[/math] и [math]Oy[/math].
2) Воспользоваться приближёнными формулами для вычисления синуса угла. Например, с помощью формулы Тейлора. Кстати, именно с помощью этой формулы калькуляторы и компьютеры вычисляют значения функции синус.
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция — arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
TL;DR: What you did was completely correct and does not rely on a right-triangle definition of the sine function.
You can use triangles to help you find values of the sine function while still using the unit circle to define the sine function.
For the angle $frac{7pi}{6},$ you have already shown how to use the unit-circle
definition to demonstrate that $sinleft(frac{7pi}{6}right)$ is the $y$-coordinate of the end of a radial segment of the unit circle, making an angle $fracpi6$ below the negative $y$-axis.
As you observed, if you drop a perpendicular from the end of that radial segment to the $y$-axis, you form a $30$-$60$-$90$-degree right triangle.
You are not using that triangle to define the sine, but you happen to know that the leg opposite the $30$-degree angle is half the length of the hypotenuse, and since the hypotenuse is the radial segment, already known to have length $1,$ the length of the opposite segment is $frac12.$
That is, the end of the radius is $frac12$ unit directly below the $y$-axis, so it has $y$-coordinate $-frac12,$ and therefore,
according to the unit-circle definition of the sine function,
$$sinleft(frac{7pi}{6}right) = -frac12.$$
If you did not already know the ratios of the sides of a $30$-$60$-$90$-degree right triangle, then (as observed already in another answer) you could derive them by cutting an equilateral triangle in half.
Most angles do not have a geometric construction that gives us exact values of their trigonometric functions, but it happens that the angle $fracpi6$ does have such a construction and it gives a particularly simple result, so we have schoolchildren memorize that result soon after introducing the idea of measuring the angles of a triangle.
Indeed, for almost any other angle there is not such a simple way to find the sine;
you can construct a triangle within the unit circle whose legs are the same magnitude as the angle’s sine and cosine, but you will not be able to write the exact values of that sine and cosine as simple ratios of integers. You cannot even write those values in any finite expression involving integers, addition, subtraction, multiplication, and division.
That is why we usually settle for an approximate value expressed as a decimal fraction.
Радианная и градусная мера угла
5 мая 2014
Сегодняшний видеоурок — один из ключевых в курсе тригонометрии. Мы расширим классическое определение синуса, косинуса и тангенса на произвольные углы (в т.ч. отрицательные), а введем новое определение — радианную меру угла.
Сегодня мы поговорим о такой теме, которая волнует всех учеников 8-9 классов, когда они начинают изучать серьезную взрослую тригонометрию. Речь идет о радианной мере угла, а также о переводе из радианной в градусную меру угла и обратно. Но, прежде чем мы начнем решать какие-то задачи на вычисления радианной меры, мне хотелось бы вспомнить старое определение, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Немного теории
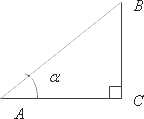
Давайте нарисуем прямоугольный треугольник, назовем его
, причем CC будет прямым:
Угол AA будет равен αalpha градусов. В этом случае, как вы помните из школьного курса геометрии, синус, косинус и тангенс будут одинаковые:
sinα=BCAB
sin alpha =frac{BC}{AB}
cosα=ACAB
cos alpha =frac{AC}{AB}
tgα=BCAC
tgalpha =frac{BC}{AC}
Как видите, классическое определение синуса, косинуса, тангенса и котангенса завязано на прямоугольном треугольнике, и αalpha в любом случае должен быть больше 0º и меньше 90º.
Несмотря на это, возникла необходимость расширить определение тригонометрических функций за пределы этого интервала от 0º до 90º. Как это происходит, и какие возникают при этом эффекты — вот сейчас об этом и поговорим.
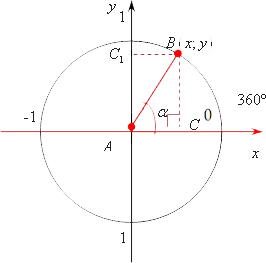
Для начала давайте рассмотрим координатную плоскость: проведем оси xx, yy, а также построим единичную окружность с центром в начале координат:
Небольшое уточнение в терминологии, что значит единичная окружность? Все очень просто. Это означает, что ее радиус равен строго 1. Другими словами, она проходит через точку (1; 0), а также (0; 1). И через две остальные точки эта окружность также проходит. Теперь нам нужно пустить от начала координат луч вдоль оси OxOx. Речь идет о положительном направлении оси OxOx. Затем мы отметим αalpha в направлении xx к yy. Разумеется, этот луч пересечет наш круг в неком значении, давайте обозначим его точкой BB. А начало координат обозначим точкой AA. Проведем из BB высоту к оси абсцисс xx. Мы получим CC. Вот мы снова получили тот же самый прямоугольный треугольник ABCABC с углом αalpha , вершина которого совпадает с началом координат.
Что такое синус?
Теперь давайте перепишем синус, косинус и тангенс с учетом всех изменений для красного треугольника. Запишем:
sinα=BCAB
sin alpha =frac{BC}{AB}
Все то же самое. Однако заметим, что BB лежит уже не в каком-то неопределенном пространстве, она имеет какие-то координаты, поскольку лежит в плоскости OxyOxy. Пусть ее координаты будут (x;y)left( x;y right). Мы не знаем точно, чему они равны, потому что не знаем угол αalpha . В таком случае длина отрезка BCBCравняется yy, т. е. ординате точки BB. Вместо BCBC мы можем записать yy, а вместо ABAB — 1. ABAB — это тот же самый радиус нашего круга, а радиус — 1. Записываем:
sinα=BCAB=yr=y
sin alpha =frac{BC}{AB}=frac{y}{r}=y
Таким образом, мы можем записать, что sinαsin alpha на самом деле равен ординате конца подвижного радиуса. Вот именно эту фразу чаще всего встречают ученики в школьных учебниках по математике. Поэтому, прежде чем двинемся дальше, давайте еще раз внимательно посмотрим на треугольник ABCABC и, в частности, на BB.
Мы провели еще одну высоту, назовем ее BC1B{{C}_{1}}. Что можно сказать про C1{{C}_{1}}, точнее, про отрезок AC1A{{C}_{1}} — это координата у BB. С другой стороны, отрезок ACAC, т. е. расстояние от AA до CC — это координата xx точки CC и, соответственно, xx точки BB. Нам несложно будет доказать, что отрезки BCBC и AC1A{{C}_{1}} равны. Тогда мы можем утверждать, что и отрезок ABAB тоже равен yy. Таким образом, с синусом мы разобрались. Действительно, синус угла αalpha равен ординате конца подвижного радиуса, проведенного в точку BB. Теперь давайте запишем те же самые выражения для косинуса и тангенса.
Что такое косинус?
Это отношение прилежащего катета (в нашем случае это катет ACAC) к гипотенузе (у нас ABAB). Но что такое ACAC? Только что мы убедились, что ACAC — это абсцисса, т. е. координата xx. А ABAB — это тот же самый радиус, т. е. 1. Запишем:
cosα=ACAB=xr=x
cos alpha =frac{AC}{AB}=frac{x}{r}=x
Что такое тангенс?
Теперь разбираемся с tgαtgalpha . Тут все еще проще. Что такое тангенс? Это отношение противолежащего катета (а нашем случае это BCBC) к прилежащему катету (в нашем случае это ACAC). Запишем:
tgα=BCAC=yx
tgalpha =frac{BC}{AC}=frac{y}{x}
Таким образом, tgtg — это отношение ординаты к абсциссе конца подвижного радиуса.
И в этот момент многие ученики наверняка спросят: «А зачем вообще вся эта сложность?». В данном случае когда BB просто задается пересечением луча с окружностью, мы можем отложить любой угол αalpha . Теперь никаких ограничений на обозначение αalpha не накладывается. Он не обязан быть углом пределах от 0º до 90º.
Вычисление радианной меры угла
Теперь, когда мы разобрались с основными определениями тригонометрических функций, перейдем непосредственно к сегодняшней теме урока.
Для начала давайте рассмотрим угол в 180º. Тогда наш луч поддет в противоположном направлении. Точка В в нашем треугольнике высекает определенную дугу окружности. Назовем ее дуга BCBC. Ее легко посчитать по формуле длины окружности:
l=2πr
l=2pi r
π ˜3,14
pi tilde{ }3,14. Но сейчас нас это не интересует. Поскольку наша окружность всегда имеет фиксированный радиус 1, то длина будет равна:
l=2π
l=2pi
Однако 2π2pi — это вся окружность, т. е. полный оборот. А мы если отступим на 180º, то получим только ее половину. Следовательно, дуга окружности будет равна:
l(180o)=2π2=π
lleft( 180{}^text{o} right)=frac{2pi }{2}=pi
И вот тут возникает замечательный эффект. Дело в том, что один и тот же угол αalpha мы можем обозначать как за 180º, т. е. использовать стандартную меру угла (а не радианную), так и длинной вот этой дуги, т. е. мы можем поставить углу αalpha соответствующее число πpi . Так вот это число πpi , т. е. другими словами, угол, измеренный не в градусах, а в длине дуги, которую этот угол высекает. Называется это радианная мера угла и обозначается πpi — радиан.
Сегодня же для того чтобы начать решать задачи на радианную меру и считать значение тригонометрических функций, просто запомните, что πpi рад = 180º. Другими словами, если вам непривычно работать с радианными значениями, то везде, где вы видите в синусах, косинусах и тангенсах конструкцию πpi , вы можете смело заменить это π на 180º и перейти к знакомой градусной от радианной меры. Давайте попробуем и сосчитаем первое выражение и найдем радианную меру:
sin π 4cos π 6tg π 3=2√2⋅3√2⋅3√=32√4sin frac{text{ }!!pi!!text{ }}{4}cos frac{text{ }!!pi!!text{ }}{6}tgfrac{text{ }!!pi!!text{ }}{3}=frac{sqrt{2}}{2}cdot frac{sqrt{3}}{2}cdot sqrt{3}=frac{3sqrt{2}}{4}
Давайте выпишем отдельно каждую из этих функций:
sin π 4=sin180∘4=sin45∘=2√2sin frac{text{ }!!pi!!text{ }}{4}=sin frac{180{}^circ }{4}=sin 45{}^circ =frac{sqrt{2}}{2}
cos π 6=cos180∘6=cos30∘=3√2cos frac{text{ }!!pi!!text{ }}{6}=cos frac{180{}^circ }{6}=cos 30{}^circ =frac{sqrt{3}}{2}
tg π 3=tg180∘3=tg60∘=3√tgfrac{text{ }!!pi!!text{ }}{3}=tgfrac{180{}^circ }{3}=tg60{}^circ =sqrt{3}
Теперь записываем все три множителя в единую конструкцию для нахождения радианного значения. Вот и все, мы получили ответ.
Переходим ко второму выражению и найдем радианную меру:
cos π 3sin π 4ctg π 6=12⋅2√2⋅3√=6√4cos frac{text{ }!!pi!!text{ }}{3}sin frac{text{ }!!pi!!text{ }}{4}ctgfrac{text{ }!!pi!!text{ }}{6}=frac{1}{2}cdot frac{sqrt{2}}{2}cdot sqrt{3}=frac{sqrt{6}}{4}
Опять записываем каждую функцию отдельно:
cos π 3=cos60∘=12cos frac{text{ }!!pi!!text{ }}{3}=cos 60{}^circ =frac{1}{2}
sin π 4=sin45∘=2√2sin frac{text{ }!!pi!!text{ }}{4}=sin 45{}^circ =frac{sqrt{2}}{2}
ctgπ6=ctg30∘=3√ctgfrac{pi }{6}=ctg30{}^circ =sqrt{3}
Опять собираем все полученные числа.
Как видите, ничего сложно в радианных мерах угла нет. Если эта тема покажется вам слишком сложной, просто запомните, что πpi рад = 180º, и везде, где вы видите πpi , можете смело писать 180º.
Еще одним важным следствием нового определения тригонометрического круга является то, что синус, косинус и тангенс могут быть отрицательными. Если раньше все сводилось к длинам катетов и гипотенузы, то теперь перед нами абсциссы и ординаты некой точки. При этом помните, что откладывание угла всегда идет в направлении от оси OxOx к оси OyOy, причем идет речь именно о положительных направлениях этих осей.
Чтобы понять и навсегда запомнить, где находится положительное направление оси, просто помните правило: туда, куда указывает стрелка при х и при у, это и есть то самое положительное направление оси.
Вот это и все, о чем я хотел рассказать в сегодняшнем видеоуроке о радианных мерах. Если вы что-то не поняли, или если этот материал показался вам слишком сложным, то пересмотрите его еще раз, попробуйте выполнить всю последовательность вычислений на нахождения радианных значений, которую мы сегодня выполнили на уроке.
Смотрите также:
- Как быстро запомнить таблицу синусов и косинусов
- Синус, косинус, тангенс, котангенс — геометрическая тригонометрия
- Метод узлов в задаче B5
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Иррациональное уравнение: учимся решать методом уединения корня
- Задача B4: строительные бригады
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!