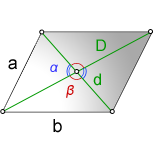
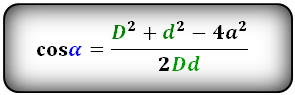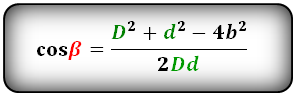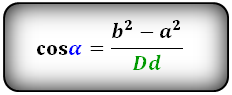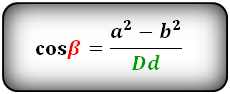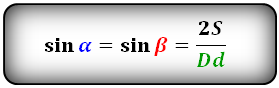Как найти синус угла между диагоналями параллелограмма

Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Частными
случаями параллелограмма являются прямоугольник и ромб. Квадрат одновременно является частным
случаем и прямоугольника и ромба, поэтому все выявленные для параллелограмма зависимости справедливы
для прямоугольника, квадрата и ромба.

На практике необходимость определения угла между диагоналями на основе прочих элементов может
возникнуть, в частности, при необходимости производства построений на местности и для перепроверки
уже проведенных построений.

Через площадь и диагонали

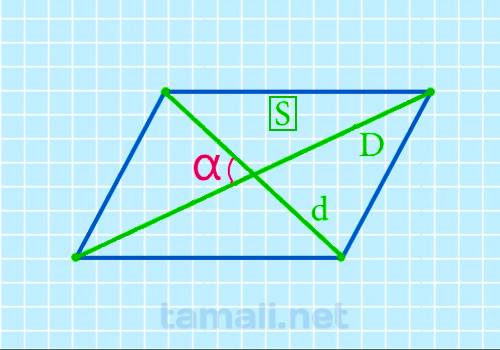
Для нахождения острого угла между диагоналями параллелограмма следует воспользоваться формулой:

sin α = 2S/(Dd)

где α – острый угол между диагоналями, S – площадь параллелограмма, D и d – его диагонали.

Приведем пример расчета по формуле для наглядного случая, когда диагонали перпендикулярны, и площадь
данного ромба равняется половине площади прямоугольника, в который данный ромб можно вписать.

При D = 20 мм, d = 10 мм, площадь описанного прямоугольника равна 20*10=200 мм², откуда S = 200/2=100 мм².

Вычисления дают sin α = 2S/(Dd) = 2*100/(20*10) = 1, откуда α = 90°. Известный факт – диагонали
ромба перпендикулярны.

Через две стороны и диагонали

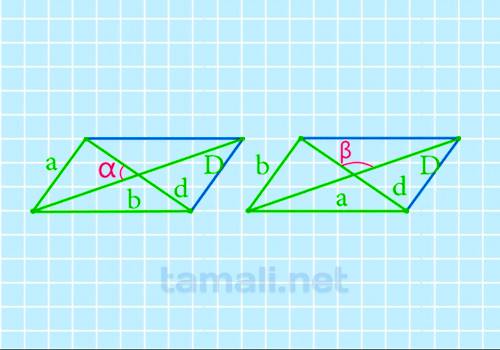
В предыдущей формуле угол определялся через диагонали и одну сторону, в данной задаче требуется
определить угол по диагоналям и 2 сторонам. Тем самым, одно из условий является избыточным, и фигура
по произвольным данным может не оказаться параллелограммом. Но для случая параллелограмма, т.е.
взаимной увязки данных, формулы таковы:

cos α = (b2-a2)/(Dd), cos β = (a2-b2)/(Dd)

где a и b – стороны параллелограмма, α и β – углы между диагоналями (взаимно дополнительные до
180°).

Пример приведем по предыдущему случаю, остается только рассчитать недостающую сторону b, которая из
простых соображений (воспользовавшись правилом длины катета против угла в 30°) оказывается равной 20
мм. Вычисляем: cos α = (b²-a²)/(Dd) = (20²-34,64²)/(40*40) = -0,5, откуда
α = 120°.

Через диагонали и сторону

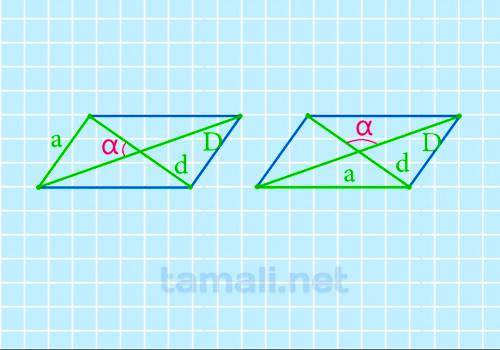
Для нахождения угла между диагоналями параллелограмма через диагонали и сторону формула такова:

cos α = (D² + d² – 4a²)/(2Dd)

где a – сторона параллелограмма, остальные обозначения прежние.

Здесь следует считаться с тем, что если в предыдущей задаче угол по условию являлся острым, в данной
задаче он может быть и тупым, с отрицательным значением косинуса угла.

Пример расчета опять-таки по наглядному случаю, когда обе диагонали равны. Это прямоугольник с
диагоналями D = 40 мм и d = 40 мм. При угле между диагоналями 120° половина диагонали составит 40/2 = 20 мм, половина высоты прямоугольника (она же – половина короткой
стороны) составит половину от половины диагонали (в прямоугольном треугольнике противолежащий углу в
30° катет равен половине гипотенузы), т.е. 10 мм, откуда половина стороны параллелограмма составит
√(20²-10²)=√300=17,32 мм, а сторона параллелограмма a = 2*17,32=34,64 мм.

Подставляем в формулу: cos α = (D² + d² – 4a²)/(2Dd) = (40²+40²-4*34,642) = ‑1600/(2*40*40) = -0,5.
Значению косинуса -0,5 соответствует угол 120°. Это же значение даст и калькулятор.

Квадрат достаточно задать одним элементом – стороной. Для задания прямоугольника необходимо задать
уже две его смежные стороны; для ромба сторону и угол между сторонами. Для задания же
параллелограмма необходимо задание 3 его взаимно независимых элементов. Это могут быть 2 смежные
стороны и угол между ними, но возможно и иное задание.

В любом четырехугольнике можно провести 2 диагонали, и они также могут входить в набор элементов для
задания фигуры. В данной статье приводятся справочные формулы для определения угла между диагоналями
параллелограмма через другие его элементы. Рассчитать же этот угол для каждого из 3 рассматриваемых
случаев позволят калькуляторы сайта, в которые необходимо ввести известные элементы, и в результате
получить синус или косинус искомого угла либо сам угол в градусах или радианах.

Задания

Версия для печати и копирования в MS Word

Формулы параллелограмма

Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.

Признаки и свойства параллелограмма

1. Противоположные стороны параллельны и равны.
2. Противоположные углы равны
3. Точка пересечения диагоналей делит их пополам.
4. Сумма углов четырехугольника прилегающих к любой стороне равна 180°
5. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
6. Сумма углов параллелограмма равна 360°
7. Каждая диагональ делит параллелограмма на два равных треугольника
8. Биссектрисы противоположных углов параллелограмма всегда параллельны
9. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)

Формулы стороны параллелограмма

Длины сторон через диагонали и угол между ними

Длина стороны через диагонали и известную сторону

Длины сторон через высоты и угол между сторонами

Формулы диагоналей параллелограмма

Длина диагонали через стороны и углы между ними

Длина диагонали через стороны и известную диагональ

Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями

Формулы углов параллелограмма

Косинус острого угла

Косинус тупого угла

Синус острого и тупого угла через площадь и стороны параллелограмма

Формулы углов между диагоналями параллелограмма

Косинус острого угла через стороны и диагонали

Косинус тупого угла через стороны и диагонали

Синус острого и тупого угла через площадь и диагонали

Параллелограмм: свойства и признаки

О чем эта статья:

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

1. В параллелограмме точка пересечения диагоналей делит их пополам.
2. Любая диагональ параллелограмма делит его на два равных треугольника.
3. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.

Как найти площадь параллелограмма:

1. S = a × h, где a — сторона, h — высота.
2. S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a 2 × sinα.
3. Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
   Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

1. Противоположные стороны параллелограмма равны.
   ABCD — параллелограмм, значит, AB = DC, BC = AD.
2. Противоположные углы параллелограмма равны.
   ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D.
3. Диагонали параллелограмма точкой пересечения делятся пополам.
   ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC.
4. Диагональ делит параллелограмм на два равных треугольника.
   ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA.
5. Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
   ABCD — параллелограмм, значит, ∠A + ∠D = 180°.
6. В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d1 2 + d2 2 = 2 × (a 2 + b 2 ).

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

1. AB = CD как противоположные стороны параллелограмма.
2. ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
3. Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
   • CO = AO
   • BO = DO

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB || CD
• AB = CD

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

1. AC — общая сторона;
2. По условию AB = CD;
3. ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB = CD
• BC = AD

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

• AC — общая сторона;
• AB = CD по условию;
• BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

• CO = OA;
• DO = BO;
• углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Параллелограмм. Формулы, признаки и свойства параллелограмма

Признаки параллелограмма

AB||CD, AB = CD (или BC||AD, BC = AD)

∠DAB = ∠BCD, ∠ABC = ∠CDA

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Основные свойства параллелограмма

∠ABC = ∠CDA, ∠BCD = ∠DAB

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:

AO = CO =	d 1
2
BO = DO =	d 2
2

AC 2 + BD 2 = 2AB 2 + 2BC 2

Стороны параллелограмма

Формулы определения длин сторон параллелограмма:

1. Формула сторон параллелограмма через диагонали и угол между ними:

2. Формула сторон параллелограмма через диагонали и другую сторону:

a =	√ 2 d 1 2 + 2 d 2 2 — 4 b 2
2

b =	√ 2 d 1 2 + 2 d 2 2 — 4 a 2
2

3. Формула сторон параллелограмма через высоту и синус угла:

4. Формула сторон параллелограмма через площадь и высоту:

Диагонали параллелограмма

Формулы определения длины диагонали параллелограмма:

d ₁ = √ a 2 + b 2 — 2 ab·cosβ

d ₂ = √ a 2 + b 2 + 2 ab·cosβ

d ₁ = √ a 2 + b 2 + 2 ab·cosα

d ₂ = √ a 2 + b 2 — 2 ab·cosα

d ₁ = √ 2 a 2 + 2 b 2 — d ₂ 2

d ₂ = √ 2 a 2 + 2 b 2 — d ₁ 2

4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:

d 1 =	2S	=	2S
d 2· sinγ	d 2· sinδ

d 2 =	2S	=	2S
d 1· sinγ	d 1· sinδ

Периметр параллелограмма

Формулы определения длины периметра параллелограмма:

P = 2 a + 2 b = 2( a + b )

P = 2 a + √ 2 d ₁ 2 + 2 d ₂ 2 — 4 a 2

P = 2 b + √ 2 d ₁ 2 + 2 d ₂ 2 — 4 b 2

3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:

Площадь параллелограмма

Формулы определения площади параллелограмма:

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Задача 31130 1. Вычислить синус угла между…