Как найти синус угла между диагоналями прямоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Прямоугольник. Формулы и свойства прямоугольника

Определение.

Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.

Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.

Стороны прямоугольника одновременно является его высотами.

Основные свойства прямоугольника

Прямоугольником могут быть параллелограмм, квадрат или ромб.

1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:

AB = CD, BC = AD

2. Противоположные стороны прямоугольника параллельны:

AB||CD, BC||AD

3. Прилегающие стороны прямоугольника всегда перпендикулярны:

AB _┴ BC, BC _┴ CD, CD _┴ AD, AD _┴ AB

4. Все четыре угла прямоугольника прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Сумма углов прямоугольника равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника имеют одинаковой длины:

AC = BD

7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:

2d² = 2a² + 2b²

8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.

9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:

10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности

11. Диагональ прямоугольника является диаметром описанной окружности

12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:

∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°

13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).

Стороны прямоугольника

Определение.

Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.

Формулы определения длин сторон прямоугольника

1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:

a = √d² — b²

b = √d² — a²

2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:

3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:

4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:

a = d sinα

b = d cosα

5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:

Диагональ прямоугольника

Определение.

Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.

Формулы определения длины диагонали прямоугольника

1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):

d = √a² + b²

2. Формула диагонали прямоугольника через площадь и любую сторону:

d =	√S² + a⁴	=	√S² + b⁴
a	b

3. Формула диагонали прямоугольника через периметр и любую сторону:

d =	√P² — 4Pa + 8a²	=	√P² — 4Pb + 8b²
2	2

4. Формула диагонали прямоугольника через радиус описанной окружности:

d = 2R

5. Формула диагонали прямоугольника через диаметр описанной окружности:

d = D_о

6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:

7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:

8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника

d = √2S : sin β

Периметр прямоугольника

Определение.

Периметром прямоугольника называется сумма длин всех сторон прямоугольника.

Формулы определения длины периметру прямоугольника

1. Формула периметру прямоугольника через две стороны прямоугольника:

P = 2a + 2b

P = 2(a + b)

2. Формула периметру прямоугольника через площадь и любую сторону:

P =	2S + 2a²	=	2S + 2b²
a	b

3. Формула периметру прямоугольника через диагональ и любую сторону:

P = 2(a + √d² — a²) = 2(b + √d² — b²)

4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:

P = 2(a + √4R² — a²) = 2(b + √4R² — b²)

5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:

P = 2(a + √D_o² — a²) = 2(b + √D_o² — b²)

Площадь прямоугольника

Определение.

Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.

Формулы определения площади прямоугольника

1. Формула площади прямоугольника через две стороны:

S = a · b

2. Формула площади прямоугольника через периметр и любую сторону:

S =	Pa — 2a²	=	Pb — 2b²
2	2

3. Формула площади прямоугольника через диагональ и любую сторону:

S = a√d² — a² = b√d² — b²

4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:

5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:

S = a√4R² — a² = b√4R² — b²

6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:

S = a√D_o² — a² = b√D_o² — b²

Окружность описанная вокруг прямоугольника

Определение.

Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.

Формулы определения радиуса окружности описанной вокруг прямоугольника

1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:

2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:

R =	√P² — 4Pa + 8a²	=	√P² — 4Pb + 8b²
4	4

3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:

R =	√S² + a⁴	=	√S² + b⁴
2a	2b

4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:

5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:

6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:

7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:

8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:

Угол между стороной и диагональю прямоугольника

Формулы определения угла между стороной и диагональю

1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

Угол между диагоналями прямоугольника

Формулы определения угла между диагоналями прямоугольника

1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:

β = 2α

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:

Источник

Прямоугольник – плоская четырёхугольная геометрическая фигура. Прямоугольник относится к
параллелограммам и обладает некоторыми свойствами:

Все внутренние углы фигуры прямые.
Противолежащие стороны попарно параллельны и равны.
Диагонали прямоугольника (отрезок, соединяющий вершины противоположных внутренних углов) равны.
Точка пересечения делит их на равные отрезки.
Диагональ делит фигуру на 2 одинаковых прямоугольных треугольника.
Диагональ делит внутренний угол (90°) на 2 угла. Накрест лежащие углы при проведенном отрезке
равны.

Острый угол между диагоналями прямоугольника через площадь
и диагональ
Угол между диагоналями прямоугольника через угол между
стороной и диагональю
Острый угол между диагоналями прямоугольника через ширину и
диагональ
Острый угол между диагоналями прямоугольника через длину и
диагональ
Острый угол между диагоналями прямоугольника через ширину и
длину
Тупой угол между диагоналями прямоугольника через длину и
диагональ
Тупой угол между диагоналями прямоугольника через ширину и
диагональ
Тупой угол между диагоналями прямоугольника через длину и
ширину

Острый угол между диагоналями прямоугольника через площадь и диагональ

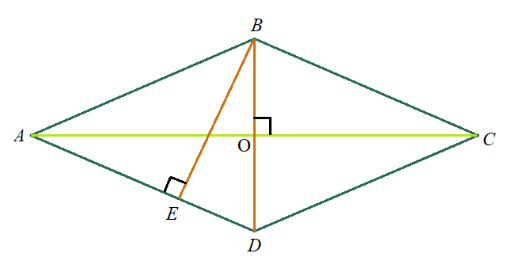
Острый угол (a) между диагоналями, зная площадь (S) и длину диагонали (d) легко можно вычислить по
формуле:

sin a = (2 * S) / d²

где d — диагональ, S — площадь прямоугольника.

Цифр после
запятой:

Результат в:

Через синус находится значение угла. По этой формуле также можно найти тупой угол между диагоналями,
так как 2 данных угла являются смежными, а синусы смежных углов равны.

Пример. Дан прямоугольник, площадь которого равна 108 см², а диагональ – 15 см.
Нужно найти острый угол между диагоналями. Необходимые значения подставляем в формулу sin a = (2 * S) / d² = (2 * 108) / 225 = 0,96. По значению синуса
находится величина острого угла между диагоналями. В данном случае она равна 73,73°.

Угол между диагоналями прямоугольника через угол между стороной и диагональю

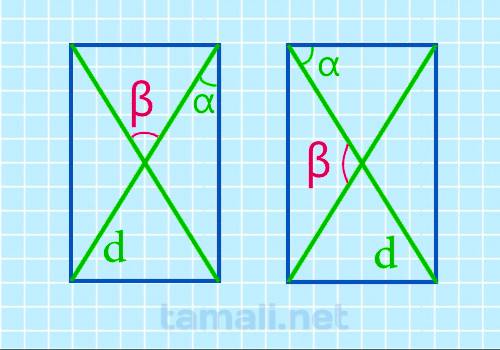
Величина нужного угла (α) в два раза больше угла (β) между стороной и диагональю по свойству углов
равнобедренного треугольника, так как диагонали при пересечении образуют 4 равнобедренных
треугольника. В равнобедренном треугольнике углы при основании (b) равны, а нужный угол является
смежным по отношению к углу при вершине (c), в таком случае c = 180 — α. Сумма углов
треугольника равна 180°. Несложно составить уравнение β+β+180-α=180, которое легко сокращается до
вида

β = 2 * α

где α — угол между стороной и диагональю.

Цифр после
запятой:

Результат в:

Пример. Пусть угол α = 15 (он может быть от 0 до 90º), тогда β = 2 * α = 2 * 15 = 30º

Острый угол между диагоналями прямоугольника через длину и ширину

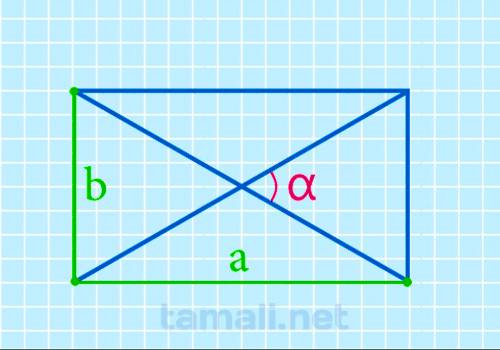
Если в задаче неизвестна длина диагонали, не нужно тратить время на ее поиски. Можно быстро найти
острый угол между диагоналями при помощи длины и ширины прямоугольника по формуле:

α = 2 arctg b / a

где b — ширина прямоугольника, a — длина прямоугольника.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник со сторонами 8 см и 6 см. Нужно построить диагонали и
найти острый угол между ними. Угол α = 2 arctg 6 / 8 = 2 arctg 0,75=73,73°.

Острый угол между диагоналями прямоугольника через ширину и диагональ

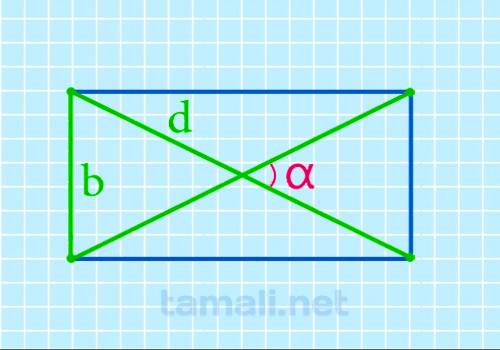
Значение нужного угла можно определить, зная длину диагонали и ширины (B) четырёхугольника, по
формуле:

α = 2 arcsin b / d

где b — ширина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Рассмотрим применение формулы в конкретной задаче. Дан прямоугольник, ширина
которого равна 3 мм, а длина диагонали – 5 мм. Необходимо найти острый угол между
диагоналями. Применив данную формулу, находим значение нужного угла: a = 2 * arcsin 0,6 = 73,73°.

Острый угол между диагоналями прямоугольника через длину и диагональ

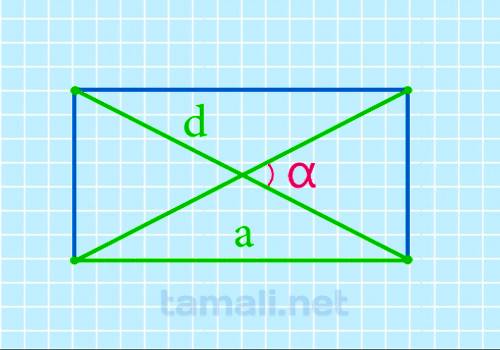
Если неизвестна ширина прямоугольника, но есть значение длины (a), можно также просто найти острый
угол между диагоналями. Формула почти идентична предыдущей:

α = 2 arccos a / d

где a — длина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. В прямоугольнике с длиной 8 см, в котором проведены диагонали длиной 10 см,
найти острый угол между диагоналями. Угол α = 2arccos 8 / 10 = 2arccos 0,8 = 73,73°.

Тупой угол между диагоналями прямоугольника через ширину и диагональ

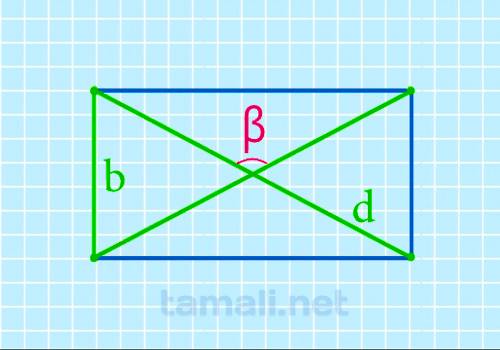
Для того чтобы быстро вычислить значение данного угла при помощи известной ширины и диагонали
прямоугольника, нужно воспользоваться следующей формулой:

β = 2 arccos b / d

где b — ширина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Известна ширина прямоугольника, она равна 8 мм. А длина диагонали равна 17
мм. Задача найти значение тупого угла между диагоналями.
Вставив данные в формулу, вы получите
правильный результат. Таким образом, β = 2 arccos 8 / 17 = 2 arccos 0,47 = 123,85°.

Тупой угол между диагоналями прямоугольника через длину и диагональ

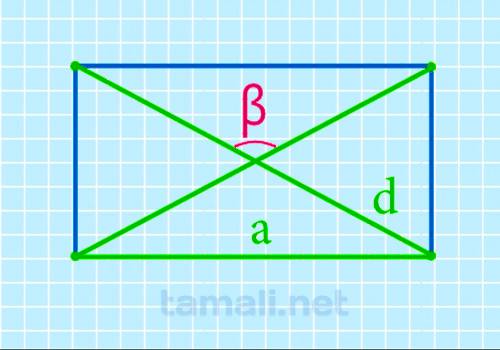
Можно, конечно, применить предыдущую формулу и найти острый угол через длину и диагональ, а потом
вычесть значение из 180°. Но есть упрощенная формула для быстрой скорости решения: тупой угол между
диагоналями

β = 2 arcsin a / d

где a — длина прямоугольника, d — диагональ.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник с длиной равной 20 см, в котором проведены диагонали
длиной 25 см. Чтобы найти нужную величину, подставляем значения в формулу: β = 2 arcsin 20 / 25 = 2 arcsin 0,8 = 106°.

Тупой угол между диагоналями прямоугольника через длину и ширину

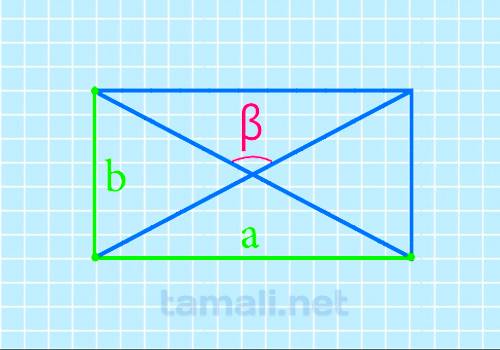
Формула для определения тупого угла между диагоналями прямоугольника через известные значения длины и
ширины такова:

β = 2 arctg a / b

где a — длина прямоугольника, b — ширина прямоугольника.

Цифр после
запятой:

Результат в:

Пример. Дан прямоугольник со сторонами 15 см и 8 см. Вычислим значение тупого угла,
подставив данные в формулу: β = 2arctg 15 / 8 = 2 arctg 0,5= 123,85°.

Стоит отметить, что при использовании указанных в статье правил нужно владеть знаниями о
тригонометрических функциях. Для того чтобы быстро определять углы, образованные пересечением
диагоналей прямоугольника, поможет именно данный список формул, которые необходимо знать наизусть.
Если на решение задач по геометрии дается небольшой промежуток времени, к примеру, контрольная или
экзамен, лучше отложить сложные алгоритмы и воспользоваться упрощенными формулами.

Параллелограмм относится к выпуклым четырехугольным геометрическим фигурам. Его основные
отличительные признаки от других фигур: равные и попарно параллельные противоположные стороны,
равные противолежащие углы. Диагонали фигуры всегда делятся точкой пересечения на равные отрезки, а
также они делят параллелограмм на 2 одинаковых треугольника. Еще одним главным свойством
четырёхугольника является то, что сумма квадратов диагоналей равна двум суммам квадратов смежных
сторон параллелограмма.

Биссектрисы внутренних углов данного четырёхугольника всегда отсекают от него равнобедренный
треугольник, а также они равны между собой. Сумма углов параллелограмма равна 360°, как и у других
четырёхугольников.
К параллелограммам относятся: квадрат (четырёхугольник с равными сторонами и
равными прямыми внутренними углами), прямоугольники и ромбы (параллелограмм с равными сторонами).
Эти фигуры часто встречаются в школьной программе на уроках геометрии.

Для чего необходимо вычисление угла между диагоналями параллелограмма

Для нахождения сторон четырёхугольника (длины и ширины).
Для нахождения площади и периметра фигуры.
Для нахождения углов между стороной и диагональю.
Для нахождения длины диагонали.

Знание свойств геометрических фигур помогает справиться с задачей любой сложности. Постоянная
практика с использованием формул способствует быстрому запоминанию информации, помогает проработать
маршруты и теоремы, которые западают.

Прямоугольник часто встречается в решении задач по геометрии. Важно знать все его свойства и уметь
пользоваться правилами и теоремами для успешного нахождения результата. Упрощенные формулы и
несколько конкретных примеров помогут определить правильный алгоритм решения и быстро найти
ответ.

Источник

четырехугольник MNKP задан координатами своих вершин : M(5;-3) N(1;2) К(4;4) P(6;1)

Четырехугольник MNKP задан координатами своих вершин : M(5;-3) N(1;2) К(4;4) P(6;1) отыскать синус угла меж его диагоналями (т.е синус угла О Я достроила четырехугольник и дорисованный угол обозначила как N1. 1) Угол МОN = УГЛУ MNN1
2) вектор МК * вектор ПН= модулю МК*модуль ПН*косинус угла меж ними
3) sin квадрат альфа +косинус квадрат альфа =1(по формуле) А подставить никак не могу. помогите. ОТвет в учебнике : 17/5 корень из 13. помогите

Клищевская Елизавета
Геометрия 2019-04-20 02:18:36 335 1

Решим по другому, вычислим площадь этого четырехугольника. Проведя диагональ в выпуклом четырехугольнике , найдем площадь треугольника — стороны

Сейчас так же треугольника
оно одинакова , а как известно площадь четырехугольника равен полу творенью диагоналей на то есть

Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике

З десь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе. Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие. Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.

1) Площади четырехугольников

Площадь параллелограмма

произведение основания на высоту

пороизведение сторон на синус угла между ними

полупроизведение диагоналей на синус угла между ними

Площадь трапеции

произведение полусуммы оснований на высоту

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

Площадь произвольного четырехугольника

Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними

2) Свойства параллелограмма

В параллелограмме:
противолежащие стороны и углы равны

диагонали пересекаются и в точке пересечения делятся пополам

3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть

3) Cредняя линия в трапеции

Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
То есть и

4) Средняя линия в равнобедренной трапеции

Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.

То есть

5) Теорема с сдвиге диагонали в трапеции

Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:

трапеция — равнобедренная равнобедренный

6) Четыре замечательные точки в трапеции

Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.

То есть точки M, N, K и P лежат на одной прямой

Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан. Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список. Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией. В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.

Колпаков Александр Николаевич. Репетитор по математике.

Александр, конечно, есть множество карманных справочников, НО! Было бы здорово сделать для репетиторов по математике скачиваемые материалы в каком-нибудь удобном формате, а также для проработки отдельно задачи к таким шпаргалкам опять же от простого к сложному.

Я выкладывал на каких-то страницах с карточками-памятками готовые теоретические материалы — файлы в формате word, по крайней мере для планиметрии точно. Просмотрите соответствующие разделы сайта. На них ведут ссылки с главной страницы. Задумываю выделить репетиторам по математике для скачивания материалов отдельный раздел сайта. Все упирается в мою занятость реальными учениками. Иначе бы уже давно реализовал все замыслы.

В этой хорошей подборке, на мой взгляд, не достает сведений по углам, например, два внутренних угла параллелограмма, связанных одной стороной в сумме дают 180 градусов.

Принципиально ли в формуле площади через диагонали брать именно меньший угол между ними? Или можно любой?

Александр, если не затруднит, очень хотелось бы получить файлик world на почту или тыкнуть ссылкой на нее. За ранее очень благодарен за титанический труд.

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

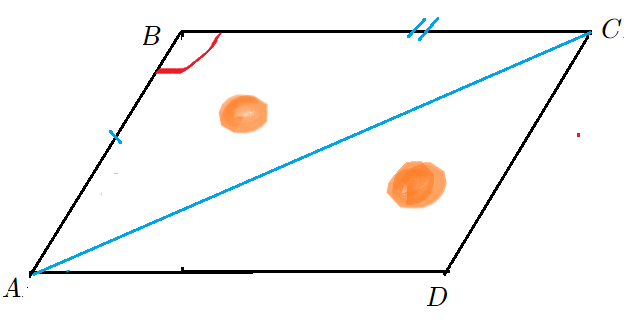
Выпуклый четырехугольник

Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь

Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
Диагонали прямоугольника равны (АС=ВD).
Диагонали пересекаются и точкой пересечения делятся пополам.
Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:

S=ab, где a и b соседние стороны прямоугольника.

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

Свойства квадрата

Диагонали квадрата равны (BD=AC).
Диагонали квадрата пересекаются под углом 90 градусов.
Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).

Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .

Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8= d 1 × 16 × 2 5 . . 2 . .

В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .

Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объекты	яблони	теплица	сарай	жилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объекты	яблони	теплица	сарай	жилой дом
Цифры	3	5	1	7

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина	Расход краски	Масса краски в одной банке	Стоимость одной банки краски	Стоимость доставки заказа
1	0,25 кг/кв.м	6 кг	3000 руб.	500 руб.
2	0,4 кг/кв.м	5 кг	1900 руб.	800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

источники:

http://ankolpakov.ru/2010/10/11/chetyrexugolniki-osnovnye-teoremy-formuly-i-svojstva-virtualnyj-spravochnik-repetitra-po-matematike/

Четырехугольники

Источник

Зная угол между диагоналями, можем найти оба угла пересечения диагонали со стороной. Если построить перпендикуляр из точки пересечения диагоналей в сторону – полуось симметрии прямоугольника, то мы получим прямоугольный треугольник, подобный тому, который образует диагональ со сторонами. Из этого треугольника видно, что углы, образованные сторонами и диагональю, в два раза меньше, чем углы при пересечении диагоналей. (рис. 56.2, 56.3)
α=γ/2
β=δ/2

При этом можно использовать свойство вертикальных углов, которое говорит о том, что острый и тупой угол в сумме дают 180 градусов, для того чтобы найти второй центральный угол.
m(

Или из прямоугольного треугольника с диагональю и сторонами найти сначала угол α и затем вычесть его из 90 градусов.
m(

Теперь имея угол, между стороной и диагональю, и саму диагональ, можно найти стороны, используя прямоугольный треугольник. (рис. 56.1) Отношение противолежащего катета – стороны к гипотенузе – диагонали является синусом угла α, следовательно, сторона прямоугольника равна произведению синуса на диагональ. Вторая сторона будет равна тогда произведению косинуса угла α на диагональ, так как она является прилежащей углу.
b=d sin⁡(α/2)
a=d cos⁡(α/2)

Те же самые формулы в обратном порядке можно использовать для угла β:
a=d sin⁡β
b=d cos⁡β

Если необходимо найти периметр и площадь прямоугольника, следует подставить в формулы вместо сторон выведенные выражения.
P=2(a+b)=2(d sin⁡β+ d cos⁡β )=2d(sin⁡β+ cos⁡β)
P=2d(sin⁡α+ cos⁡α)
S=ab=d sin⁡β* d cos⁡β=d^2 sin⁡β cos⁡β
S=d^2 sin⁡α cos⁡α

Для того чтобы найти радиус окружности, которую можно описать вокруг прямоугольника, нужно разделить его диагональ на два, так как она совпадает с диаметром. (рис.56.3)
R=d/2

Источник

Учебник

Геометрия, 9 класс

Формулы площадей через синус угла

Основные свойства площадей фигур:

Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков — равновеликие.
Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
Площадь прямоугольника равна произведению ширины на длину … произведение сторон.

Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.

Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут «увидеть» площадь.
Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь — сумма площадей кусков.
Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также «сумма кусков».
Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
$S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$

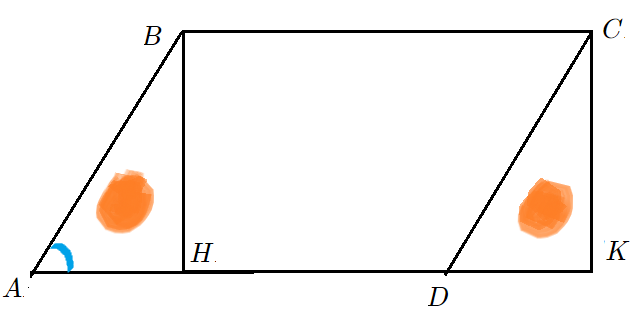
Теорема «о площади параллелограмма и треугольника через синус угла»:

Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$

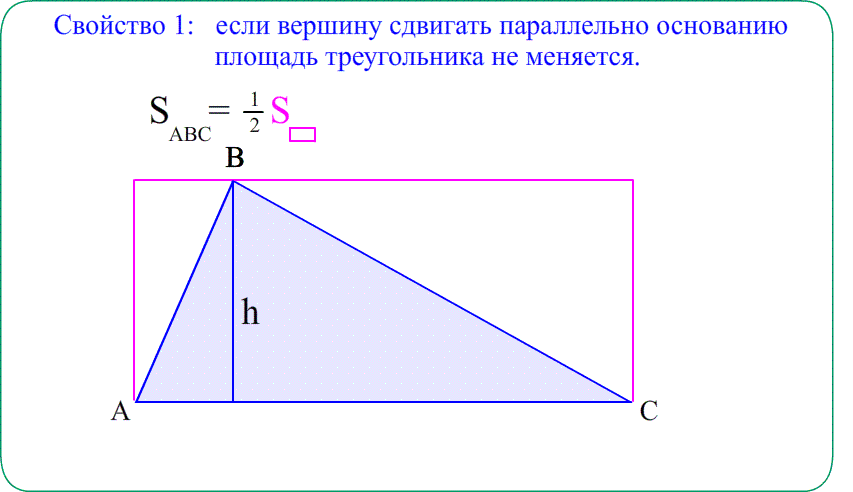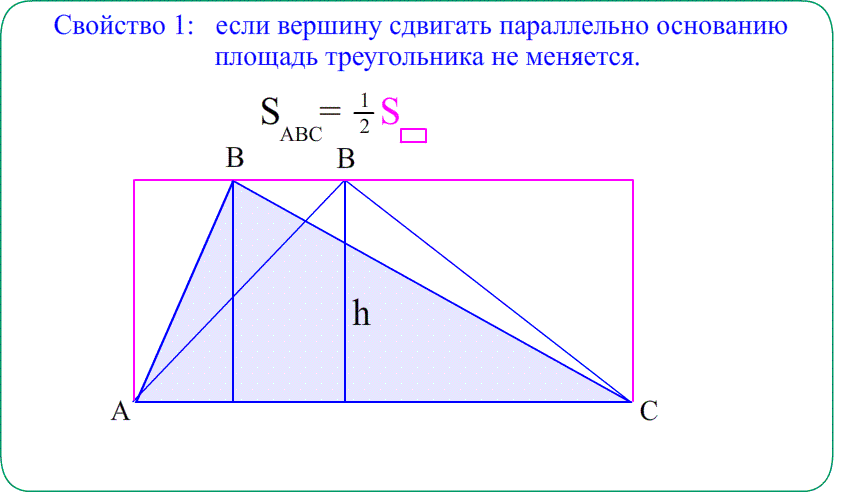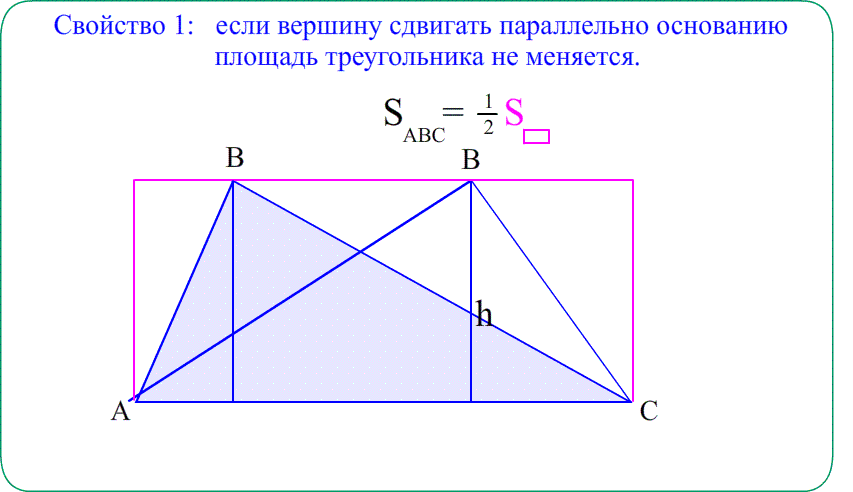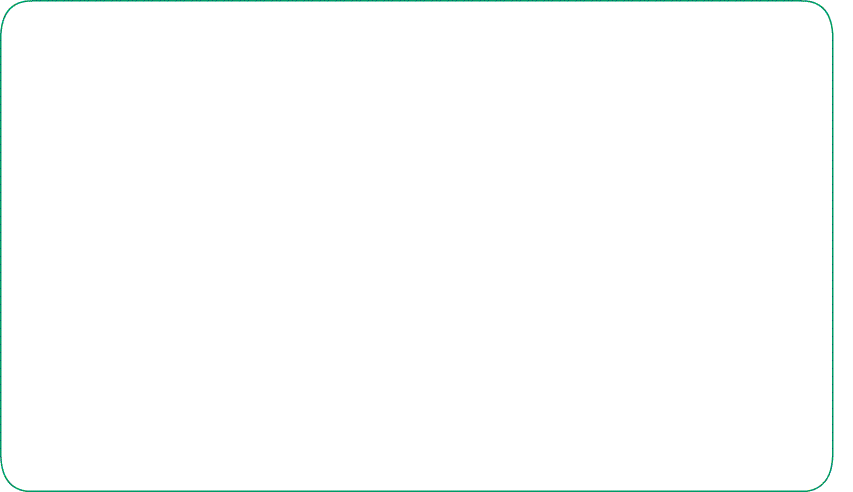
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.

Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.

Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$

Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:

$frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
$S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

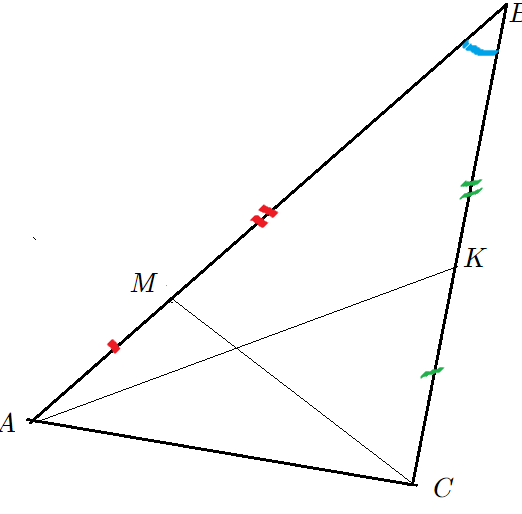
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.

Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
$frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
$frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$

Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?

Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?

Теорема «о площади четырехугольника через диагонали и синус угла»:

Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$

Формулы площади треугольника:

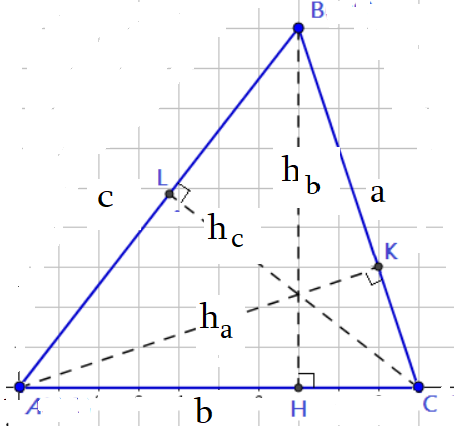
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.

$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.

$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .

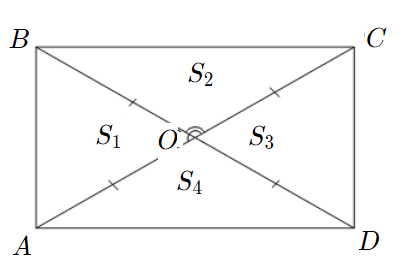
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.

Дано: $ABCD$ — прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
$bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
$bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
$sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
… тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
$S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$

Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.

Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
$bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый «состав» углов. Все прямоугольные,
Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
Для нахождения площади ромба нам нужно найти вторую диагональ.
$bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$

Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$

Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
$a=sqrt{400}=20$ Ответ: $a=20$
2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$

Интерактивные Упражнения

Источник