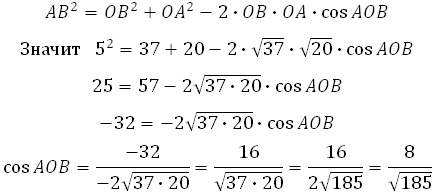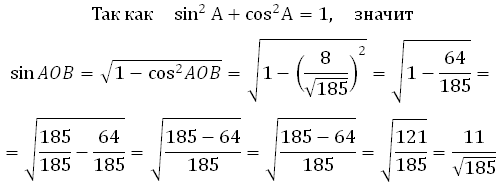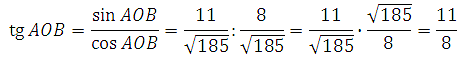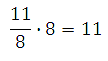Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
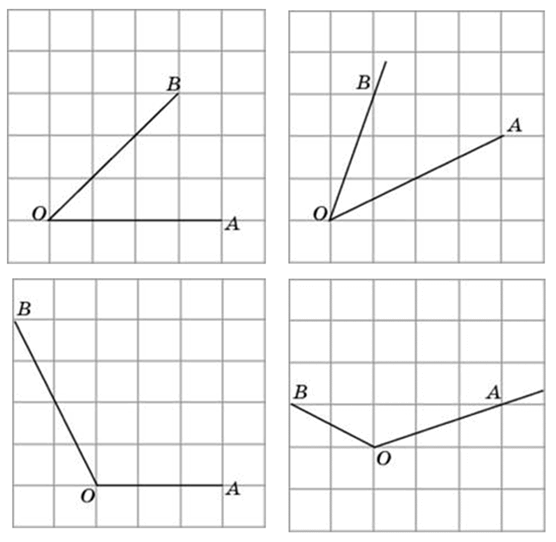
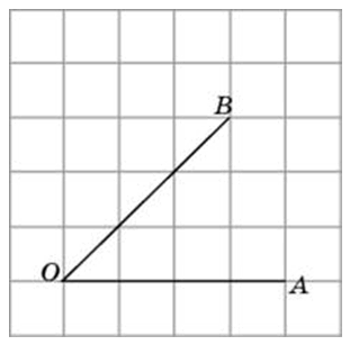
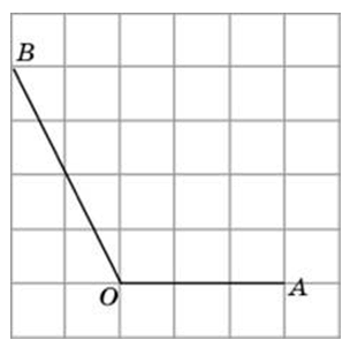
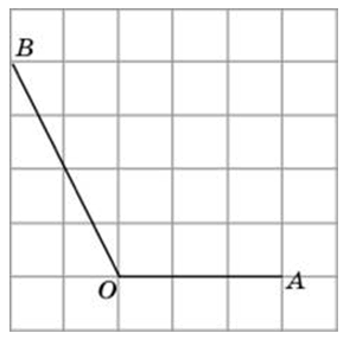
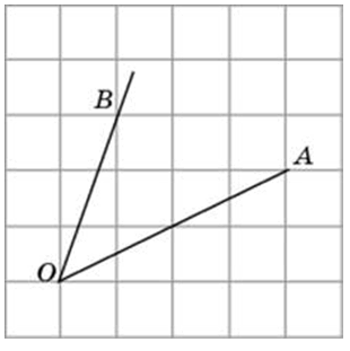
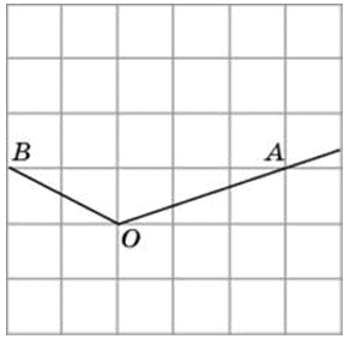
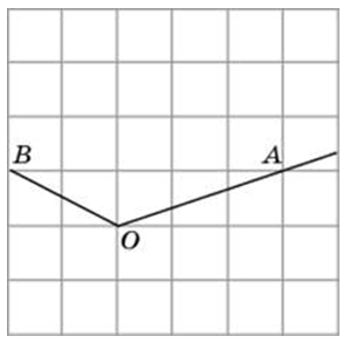
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
Итак, рассмотрим задание:
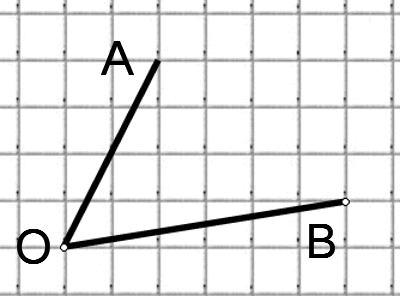
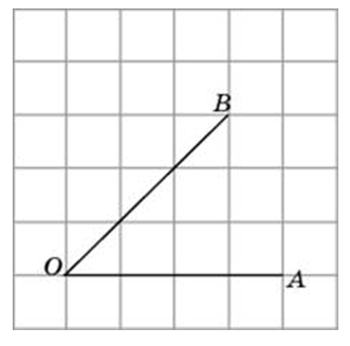
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
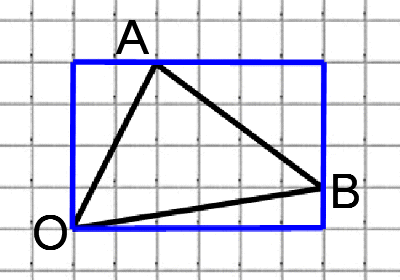
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Задания
Версия для печати и копирования в MS Word
Тип 12 № 3853
i
На клетчатой бумаге с размером клетки 1 × 1 изображён острый угол. Найдите синус этого угла.
Спрятать решение
Решение.
Достроим угол до прямоугольного треугольника с катетами 3 и 4. По теореме Пифагора найдём длину гипотенузы:
Синус угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе, значит, он равен:
Ответ: 0,6.
Источник: ВПР по математике 8 класса 2020 года. Вариант 7
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
04
Окт 2012
03 Задание (2022)ПЛАНИМЕТРИЯ
Натолкнулась в Открытом банке заданий по математике на задачу, которую в прошлом году не встречала:
Задание B7 (№ 27458) из Открытого банка заданий для подготовки к ЕГЭ по математике:
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на 
Давайте сделаем дополнительное построение:
Величина угла АОВ равна сумме углов 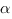
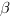
Примем размер клетки равным 1, и найдем длину ОВ из треугольника ОВС и длину АО из треугольника АОС:

По формуле для косинуса суммы имеем:
Вспомним соотношения для сторон и углов в прямоугольном треугольнике:
косинус угла равен отношению прилежащего катета к гипотенузе;
синус угла равен отношению противолежащего катета к гипотенузе.
Тогда из треугольника ВОС:
Из треугольника АОС:
Подставим эти значения в формулу для косинуса суммы:
В ответе запишем значение косинуса, умноженное на 
Ответ: -2
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ГЕОМЕТРИЯ. Часть В»

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
Итак, рассмотрим задание:
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Решение задачи
Данный урок показывает, как, используя понятие синуса угла: синус угла – это отношение противоположного катета прямоугольного треугольника к его гипотенузе – определить синус произвольного угла изображенного на рисунке. Для решения задачи необходимо провести перпендикуляр через одну из сторон данного угла, тем самым получив прямоугольный треугольник. Используя клеточки на изображенном рисунке можно с легкостью определить длину одного из катетов. После этого можно найти дину гипотенузы (чаще всего для этого используется длина второго катета и теорема Пифагора). После того как длина гипотенузы была определена арифметические вычисления приводят к получению итогового ответа.
Решение данной задачи рекомендовано для учащихся 7-х классов при изучении тем «Треугольники» («Треугольники»), «Соотношение между сторонами и углами треугольника» («Виды треугольников», «Основные свойства прямоугольных треугольников»), для учащихся 8-х классов при изучении темы «Подобные треугольники» («Синус, косинус и тангенс острого угла прямоугольного треугольника»), «Площадь» («Теорема Пифагора»), для учащихся 9-х классов при изучении темы «Соотношение между сторонами и углами треугольника. Раздел 1. Синус, косинус и тангенс угла» («Синус, косинус и тангенс угла. Основное тригонометрическое тождество»). При подготовке к ОГЭ урок рекомендован при повторении тем «Треугольники», «Соотношение между сторонами и углами треугольника», «Подобные треугольники», «Соотношение между сторонами и углами треугольника. Раздел 1. Синус, косинус и тангенс угла».
Условие задачи
На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла.
Решение
Синус угла на рисунке равен синусу смежного с ним угла, который легко найти, достроив на чертеже прямоугольный треугольник с катетами 4 и 3 и гипотенузой 5.
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе.
Ответ:
0,8.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Решение. Задание 3, Вариант 3» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
|
Чтобы найти синус угла по клеточкам надо на миллиметровой бумаге циркулем начертить окружность произвольного радиуса предпочтительно кратного десяти. Построить искомый угол, ведя отсчет от верхнего правого квадранта. Из точки пересечения луча угла с окружностью опустить перпендикуляр на ось абсцисс. Посчитать количество клеток пересекаемых этим перпендикуляром и разделить это число на количество клеток в радиусе окружности, это и будет синус угла. Знак взять плюс если луч угла проходит в первом или во втором квадрантах и знак минус для третьего и четвертого . Знаете ответ? |