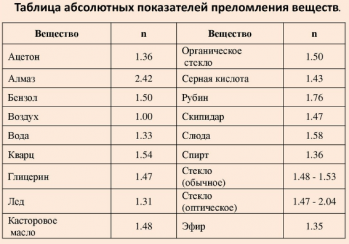
Как найти синус угла полного внутреннего отражения - Исправление недочетов и поиск решений вместе с Examum.ru

Полное внутреннее отражение (англ. total internal reflection) — это явление, при котором свет, падающий на границу двух сред из среды с большим показателем преломления под углом, превышающим предельный угол α_пр , не преломляется, а полностью отражается, так что энергия падающего света отражается в первую среду.

Вам интересно, почему полное отражение электромагнитных волн зависит от различных сред и углов? А как можно вычислить угол, при которым происходит полное внутреннее отражение? Именно об этом вы узнаете далее из моей статьи.

Описание явления и формула

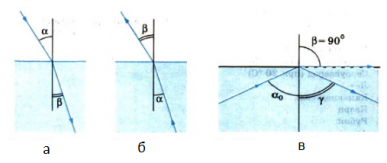
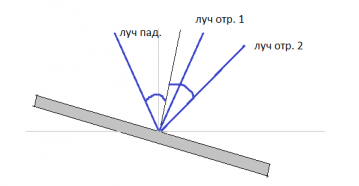
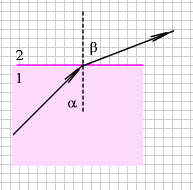
Свет, то есть электромагнитная волна в диапазоне от 380 нм до 780 нм, достигая границы сред, может претерпевать два явления: отражение и преломление (рис. 1.).

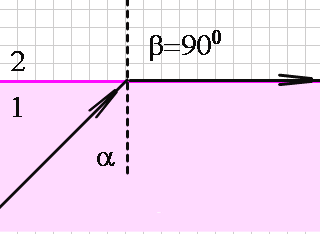
Рис. 1. Свет, падающий на границу между средами с различными показателями преломления, может претерпевать два явления: отражение и преломление.

Однако иногда случается, что явление преломления не происходит. Давайте рассмотрим это подробнее. В первой среде, показатель преломления которой будет больше, чем во второй, поместим источник света под малым углом падения. Затем вы заметите, что оба явления имеют место. Теперь давайте постепенно увеличивать угол падения. В определенный момент мы достигнем ситуации, когда угол преломления будет равен 90° и свет будет «скользить» через границу сред (рис. 2.). Угол падения в этом случае называется предельным углом.

Рис. 2. Свет, падающий на границу сред под граничным углом, «скользит» через границу

Предельный угол α_пр (или критический угол) — максимальный угол падения света на границе двух сред, при котором происходит явление преломления.

Если продолжать увеличивать угол падения, то явление преломления не произойдет. Мы будем наблюдать только отражение. Это называется полным внутренним отражением. Это явление было описано в первой половине 19 века независимо друг от друга Жаком Бабинэ и Жаном-Даниэлем Колладоном.

Рис. 3. Пример полного внутреннего отражения света

Если n1 > n2 и угол падения больше предельного угла α_пр, то преломление отсутствует, т.е. происходит полное внутреннее отражение (см. рисунок 3).

Поэтому остается вопрос, каков вычислить этот предельный угол? Это максимальный угол падения, при котором мы еще можем говорить о явлении преломления. Затем, пройдя через границу сред, луч «скользит вдоль границы», и угол преломления составляет 90° (рис. 2.). Таким образом, закон преломления света принимает вид: sin ( α_пр ) / sin ( 90° ) = n₂ / n₁ . Преобразуя приведенную выше формулу, получаем: sin ( α_пр ) = sin ( 90° ) * ( n₂ / n₁ ) = n₂ / n₁ .

Предельным углом для вычисления полного отражения является угол, обратный функции синуса и отношения показателей преломления оптически менее плотной и оптически более плотной среды, то есть α_пр = arcsin ( n₂ / n₁ ) .

Таким образом, если световая волна падает на границу двух сред таким образом, что угол падения больше arcsin ( n₂ / n₁ ), то мы говорим о полном внутреннем отражении света.

Но как именно можно определить, является ли среда оптически более плотной или менее плотной?

Закон преломления света можно использовать для описания изменения направления электромагнитных волн при их прохождении через различные среды. Прежде всего, необходимо дать некоторые определения.

В оптике показатель преломления n указывает на отношение длины волны λ или фазовой скорости c света в вакууме к скорости света в материале или среде ( c_ср ). Это определяет оптически более плотные среды и оптически менее плотные среды. Соответственно, показатель преломления без единиц измерения можно определить по следующей формуле: n = c / c_ср = λ / λ_ср .

Формула закона преломления света, как известно, определяется как отношение угла падения α и угла преломленного света β. Это должно быть равно отношению показателей преломления, то есть sin α / sin β = n₂ / n₁ .

В случае полного внутреннего отражения угол падения или предельный угол α_пр равен отношению показателя преломления оптически более плотной среды к оптически менее плотной среде.

Это означает, что если n₁ > n₂, то при достаточно большом угле падения α , β уже не соответствует действительному (вещественному) числу: sin β = sin α * n₁/n₂ > 1.

Примеры расчёта

Давайте перейдем от теории к практике и проиллюстрируем, как можно рассчитать предельный угол полного внутреннего отражения. В примере электромагнитная волна из воды попадает в воздух.

Показатель преломления воды составляет около 1,333 при 20°C, тогда как показатель преломления воздуха равен 1,000292. Из этого следует, что в данном примере вода является оптически более плотной средой, а воздух — оптически менее плотной средой, то есть n_воды > n_{воздуха} .

Поэтому предельный угол α_пр может быть рассчитан с помощью обратной функции синуса и отношения показателей преломления воздуха и воды, то есть α_пр = arcsin ( 1,000292 / 1,333 ) = 48,6^° .

На основе определенного предельного угла можно определить три результирующие области:

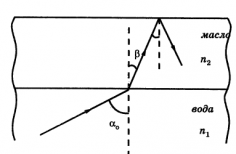
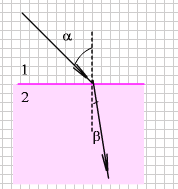
Если свет проникает через воду и попадает в оптически менее плотную среду — воздух под углом меньше 48,6°, то можно заметить, что часть света отражается, а часть преломляется в пограничном слое (см. рисунок 4).

Рис. 4. Переход света из воды в воздух α < 48,6°

Однако если свет падает на воздух с определенным предельным углом равным 48,6°, часть электромагнитной волны пройдет точно на границе раздела сред. Другая часть отразится (см. рисунок 5).

Рис. 5. Переход света из воды в воздух с α=48,6 градусов

Если угол падения теперь больше предельного угла α_пр , равного 48,6°, мы говорим о полном внутреннем отражении. В этом случае свет полностью отражается на границе раздела сред, больше не преломляется и, следовательно, больше не проникает в воздух.

Однако существуют некоторые ограничения, чтобы не нарушить общее отражение. Оптически менее плотная среда должна иметь определенную минимальную толщину. Кроме того, оптически менее плотная среда не должна быть абсорбирующей.

Коэффициент экстинкции k используется для описания ослабления электромагнитных волн, например, за счет рассеяния или поглощения. Он определяется как произведение показателя преломления n и коэффициента поглощения κ, то есть k = n * κ .

Применение

Далее рассматриваются некоторые примеры практического применения принципа полного внутреннего отражения электромагнитных волн.

Эффект полного внутреннего отражения особенно полезен для оптических волокон, таких как оптоволоконные кабели. Оптоволоконные кабели состоят из сердечника и оболочки. Сердечник из стекловолокна является оптически плотной средой, а оболочка — оптически менее плотной средой. Благодаря полному внутреннему отражению, свет внутри оптоволоконного кабеля почти полностью отражается от оболочки и остается в сердцевине.

Известный всем кабельный интернет также передается с помощью оптоволоконных кабелей. Здесь электрические сигналы преобразуются в электромагнитные импульсы с помощью электрооптических преобразователей.

Призмы часто используются в оптике. Эти призмы обладают физическим эффектом дисперсии. Благодаря различным частотам электромагнитных волн, призмы могут быть использованы для разделения света на его спектр или спектральные цвета.

Они также используются для определения расстояния от Земли до Луны. Призма, которая служит здесь отражателем, находится на Луне. Если теперь направить лазер с Земли на эту призму, она отразит лазерный луч и отправит его обратно на Землю. Исходя из характеристики скорости света c, равной 300 000 км/с, и расчетного времени возврата t, равного примерно 2,55 с, получается, что расстояние составляет: s = c * t = 300 000 * (2,55 / 2) ≈ 382 500 км .

Другой важной областью, в которой явление полного внутреннего отражения нашло ряд применений, является медицина. Здесь в первую очередь следует отметить возможность заглянуть внутрь тела без хирургического вмешательства. Для этой цели служит устройство, состоящее из нескольких оптических волокон, объединенных вместе. Это нашло применение прежде всего в эндоскопии, которая позволяет проводить неинвазивное обследование, а также брать биопсию и проводить небольшие хирургические вмешательства.

Одно из самых популярных и известных применений этого явления — ювелирная промышленность. Он заключается в придании полированному камню соответствующей формы и покрытии его симметричными плоскостями, так что внутри камня происходит полное внутреннее отражение, и около 80% лучей преломляются. Это позволяет наблюдать характерный блеск бриллиантов

Список использованной литературы

При написании статьи использовались следующие источники информации:

Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
Учебник, Физика, 8 класс. Л.А. Исаченкова, Ю.Д. Лещинский, В.В. Дорофейчик
Кикоин И. К., Кикоин А. К. Физика – 9, Москва, Просвещение, 1990.

Источник

Преломление света.

Закон преломления (частный случай).
Обратимость световых лучей.
Закон преломления (общий случай).
Полное внутреннее отражение.
Разберем задачи ЕГЭ по теме: Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление — свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда — читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет — во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

к оглавлению ▴

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе «воздух–среда»

В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль) к поверхности среды. Луч , как и раньше, называется падающим лучом, а угол alpha между падающим лучом и нормалью — углом падения. Луч — это преломлённый луч; угол beta между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла n=1,6 , а для воды n=1,33 . Вообще, у любой среды ; показатель преломления равен единице только в вакууме. У воздуха , поэтому для воздуха с достаточной точностью можно полагать в задачах n=1 (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход «воздух–среда»).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=n$ . (1)

Поскольку из соотношения (1) следует, что , то есть — угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: . И вот оказывается,что

$n=frac{displaystyle c }{displaystyle v }$ . (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle c }{displaystyle v }$ . (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

к оглавлению ▴

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе «среда–воздух»

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла alpha к синусу угла beta по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол beta стал углом падения, а угол alpha — углом преломления.

В любом случае, как бы ни шёл луч — из воздуха в среду или из среды в воздух — работает следующее простое правило. Берём два угла — угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

к оглавлению ▴

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления $n_{displaystyle 1}$ в среду 2 с показателем преломления $n_{displaystyle 2}$ . Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:

Оказывается, оба этих случая охватываются одной формулой — общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle n_{displaystyle 2}}{displaystyle n_{displaystyle 1}}$ . (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода «воздух–среда» является частным случаем данного закона. В самом деле, полагая в формуле (4) $n_{displaystyle 1}=1, n_{displaystyle 2}=n$ , мы придём к формуле (1).

Вспомним теперь, что показатель преломления — это отношение скорости света в вакууме к скорости света в данной среде: $n_{displaystyle 1}=c/v_{displaystyle1}, n_{displaystyle 2}=c/v_{displaystyle2}$ . Подставляя это в (4), получим:

$frac{displaystyle sinalpha}{displaystyle sinbeta }=frac{displaystyle v_{displaystyle 1}}{displaystyle v_{displaystyle 2}}$ . (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

к оглавлению ▴

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление — полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

Рис. 5. Полное внутреннее отражение

Луч $SO_{displaystyle 1}$ падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч $O_{displaystyle 1} A_{displaystyle 1}$ ) и частично отражается назад в воду (луч $O_{displaystyle 1} B_{displaystyle 1}$ ). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча $S O_{displaystyle 2}$ больше. Этот луч также разделяется на два луча — преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч $O_{displaystyle 2} A_{displaystyle 2}$ будет тусклее, чем луч $O_{displaystyle 1} A_{displaystyle 1}$ (то есть получит меньшую долю энергии), а отражённый луч $O_{displaystyle 2} B_{displaystyle 2}$ — соответственно ярче, чем луч $O_{displaystyle 1} B_{displaystyle 1}$ (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая — преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения $alpha _{0}$ , которому отвечает угол преломления $90^{circ}$ . В данной ситуации преломлённый луч должен был бы пойти параллельно поверхности воды, да идти уже нечему — вся энергия падающего луча целиком досталась отражённому лучу .

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение $alpha _{0}$ — все такие лучи целиком отражаются назад в воду. Угол $alpha _{0}$ называется предельным углом полного отражения.

Величину $alpha _{0}$ легко найти из закона преломления. Имеем:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$ .

Но $sin90^{circ}=1$ , поэтому

$sinalpha _{0}=frac{displaystyle 1}{displaystyle n}$ ,

откуда

$alpha _{0}=arcsinfrac{displaystyle 1}{displaystyle n}$ .

Так, для воды предельный угол полного отражения равен:

$alpha _{0}=arcsinfrac{displaystyle 1}{1,33} approx 48,8^{circ}$ .

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности — вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

к оглавлению ▴

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина $alpha = 30^{circ}$ . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления $beta = 90^{circ}$ Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
$alpha = 30^{circ}$
$beta = 90^{circ}$
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла $alpha_1=180^{circ}-(alpha+90^{circ})=90^{circ}-alpha.$

$alpha_1=90^{circ}-30^{circ}=60^{circ}.$

Тогда угол падения луча на плоское зеркало будет равен
$90^{circ}-alpha_1=90^{circ}-60^{circ}=30^{circ}.$

То есть угол падения равен $alpha=30^{circ}$ .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен $2alpha=60^{circ}$ (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
$frac{sin{2alpha}}{sinbeta}=frac{1}{n}$
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

$n=frac{sinbeta}{sin2alpha}$

$n=frac{sin90^{circ}}{sin(2cdot 30^{circ})}=frac{sin90^{circ}}{sin60^{circ}}approx 1,15$

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

$frac{1}{d}+frac{1}{f}=frac{1}{F} (1)$

Так как источник света расположен на расстоянии то $frac{1}{d}rightarrow 0.$

Тогда формула тонкой линзы (1) примет вид $frac{1}{f}=frac{1}{F},$ следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

$frac{sinalpha}{sinbeta}=frac{n}{1}=n (1).$

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

$frac{sinbeta}{singamma}=frac{1}{n} (2).$

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и .

Так как правые части этих уравнений равны, то

Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Угол преломления	Скорость света в стекле

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

$frac{sinalpha}{sinbeta}=frac{n}{1}=n.$

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение sinbeta так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления $v_{cp}=frac{c}{n},$ где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с n_1=1,5 в вещество с n_2=1,2 ?

Решение.

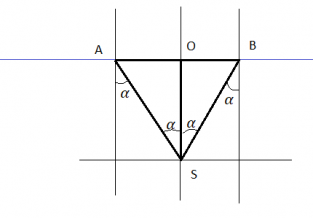
Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

$frac{sinalpha_{np}}{sinbeta}=frac{n_2}{n_1} (1)$

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления $beta=90^{circ}$ . С учетом того, что $sin90^{circ}=1$ уравнение (1) примет вид:

$sinalpha_{np}=frac{1,2}{1,5}=0,8$

$sinalpha_{np}=0,8$

Ответ: 0,8.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Основные законы геометрической оптики были известны задолго до установления физической природы света. Большая часть из них выводятся из общего принципа, описывающего поведение волн. Впервые этот принцип выдвинул современник Ньютона Христиан Гюйгенс.

Принцип Гюйгенса

Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

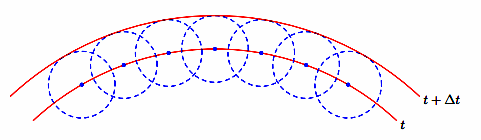
Чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t + ∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Этот принцип подходит для описания волн любой природы (световых, механических, электромагнитных и пр.).

Для механических волн принцип Гюйгенса имеет наглядное толкование: частицы среды, до которых доходят колебания, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Закон прямолинейного распространения света

В оптически однородной среде свет распространяется прямолинейно.

Опытным доказательством этого закона служат резкие тени, отбрасываемые непрозрачными телами при освещении светом источника небольших размеров («точечного источника»).

Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.

Внимание!

Законы геометрической оптики выполняются приближенно при условии, что размеры препятствий на пути световых волн много больше длины волны. Так, закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через очень малые отверстия.

Пример №1. Здание, освещенное солнечными лучами, отбрасывает тень длиной L = 36 м. Вертикальный шест высотой h = 2,5 м отбрасывает тень длиной l = 3 м. Найдите высоту H здания.

Так как шест и здание расположены вертикально, они параллельны. Так как на них светит один и тот же источник света, то угол падения лучей одинаков. Следовательно, треугольники, образованные стеной зданий, лучом солнца и землей, а также землей, лучом солнца и шестом, подобны. Отсюда можно сделать вывод, что отношение высоты здания к высоте шеста будет отношению длины тени здания к длине тени шеста:

Hh=Ll

H2,5=363=12

H=12·2,5=30 (м)

Закон отражения света

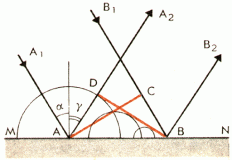
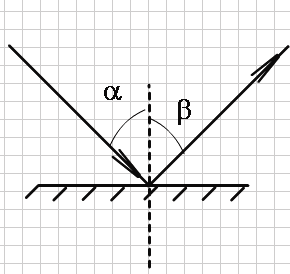
Рассмотрим отражение плоской волны (см. рис. ниже).

Пусть:

MN — отражающая поверхность.
A₁A и B₁B — два параллельных луча падающей плоской волны.
AC — волновая поверхность плоской волны.
α и γ— угол падения и отражения лучей A₁A и B₁B.

Определение

Плоская волна — волна, волновые поверхности которой представляют собой плоскости.

Угол падения — угол между падающим лучом и перпендикуляром к отражающей поверхности.

Угол отражения — угол между перпендикуляром к отражающей поверхности и отраженным лучом.

Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности AC достигают отражающей границы неодновременно. Возбуждение колебаний в точке A начинается раньше, чем в точке B, на время Δt=CBv (v — скорость волны).

В момент, когда волна достигнет точки B, и в этой точке начнется возбуждение колебаний, вторичная волна в точке A уже будет представлять собой полусферу радиусом r = AD = v∆t = CB. Радиусы вторичных волн от источников, находящихся между точками A и B, меняются так, как показано на рисунке выше.

Огибающей вторичных волн является плоскость DB, касательная к сферическим поверхностям. Она является волновой поверхностью отраженной волны. Отраженные лучи AA₂ и BB₂ перпендикулярны волновой поверхности DB. Между ними образуется угол γ, являющийся углом отражения.

Так как AD = CB и треугольники ADB и ACB прямоугольные, то углы DBA и CAB равны. Но угол α= ∠CAB, а γ= ∠DBA как углы с перпендикулярными сторонами. Следовательно, α=γ.

Закон отражения света

Угол падения равен углу отражения. Падающий луч, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.

Пример №2. Луч света падает на плоское зеркало. Угол падения α равен 20°. Чему равен угол между падающим и отражённым лучами?

Поскольку, согласно закон отражения света, угол падения равен углу отражения, то угол между падающим и отражённым лучами равен удвоенному углу α. Следовательно, он равен 40°.

Закон преломления света

На границе двух разнородных сред свет меняет направление распространения. Часть его энергии возвращается в первую среду, то есть, происходит отражение света. Если же вторая среда прозрачна, то часть света проходит через границу, разделяющую первому и вторую среду. При этом он меняет свое направление. Это явление называется преломлением света.

Преломление света на границе двух сред легко продемонстрировать с помощью стакана, воды и карандаша. Если опустить карандаш в пустой стакан, то он будет выглядеть таким же прямым, как и всегда (см. рисунок слева). Если же опустить карандаш в стакан, заполненный водой, мы увидим, что его часть под водой будто бы «преломилась».

Закон преломления света, который определяет взаимное расположение луча падающего, луча преломленного и перпендикуляра, восстановленного в точке падения, был открыт опытным путем в XVII веке. Но его можно доказать, основываясь на принципе Гюйгенса.

Известно, что скорость света достигает максимального значения только в вакууме. При распространении в среде скорость света снижается. Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость распространения волны в первой среде как v1, а во второй — как v2.

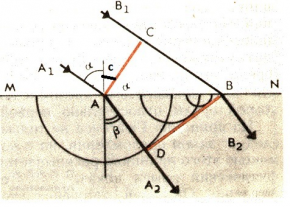
Пусть на плоскую границу раздела двух сред (к примеру, из воздуха в воду) падает плоская световая волна (см. рисунок выше). Волновая поверхность AC перпендикулярна лучам A₁A и B₁B. Поверхности MN сначала достигнет луч A₁A. B₁B достигнет ее через некоторое время, которое можно определить отношением:

Δt=CBv1

В момент, когда вторичная волна в точке B только начинает возбуждаться, волна от точки A уже имеет вид полусферы, радиус которой определяется выражением:

AD=v2Δt

Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае, ею является плоскость BD. Она является огибающей вторичных волн.

Угол падения α равен CAB в треугольнике ABC (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно:

CB=v1Δt=ABsinα

Угол преломления β равен углу ABD в треугольнике ABD. Поэтому:

AD=v2Δt=ABsinβ

Поделим первое выражение на второе и получим:

sinαsinβ=v1v2=n

Закон преломления света

Падающий луч, луч преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред.

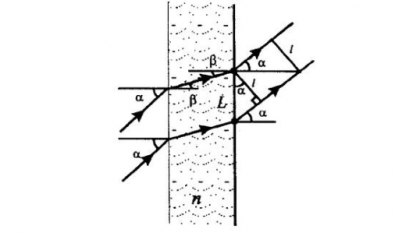
Пример №3. Угол падения параллельных лучей на плоскопараллельную пластинку равен 60^о. Найдите расстояние между точками, в которых из пластины выходят параллельные лучи, если расстояние между лучами, прошедшими сквозь пластину, равно 0,7 м.

Сначала построим рисунок хода лучей до пластины, внутри нее и после нее. Расстояние между лучами, прошедшими сквозь пластину, обозначим за l. Оно равна длине перпендикуляра, соединяющего эти лучи.

Значение величины угла β, который составляет нормаль к пластине и направлением распространения луча в ней, определяется законом преломления света:

sinαsinβ=n

Луч выходит из пластины под некоторым углом γ таким, что:

sinβsinγ=1n

Следовательно:

n=sinγsinβ=sinαsinβ

Отсюда: sinγ=sinα или γ= α. Если вспомнить геометрические законы, можно сделать вывод, что расстояние между пластинами, являющееся гипотенузой прямоугольного треугольника, можно вычислить путем деления катета на косинус угла между ним и гипотенузой:

L=lcos60°=0,70,5=1,4 (м)

Величина n — относительный показатель преломления.

Физический смысл показателя преломления заключается в том, что он равен отношению скоростей света в средах, на границе между которыми происходит преломление.

n=v1v2

Различают также абсолютный показатель преломления — показатель преломления среды относительно вакуума. Он равен синусу угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.

Поскольку в вакууме скорость света максимальна, абсолютный показатель преломления можно выразить формулой:

n=cv1

где v1 — скорость света в среде, c — скорость света в вакууме.

Между абсолютными и относительными показателями преломления есть взаимосвязь. Пусть скорость распространения света в первой среде равна v1, во второй — v2. Тогда абсолютные показатели преломления для первой и второй среды равны:

n1=cv1

n2=cv2

Тогда относительный показатель преломления при переходе света из первой среды во вторую будет равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:

n=v1v2=n2n1

Внимание!

Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой, а среду с большим абсолютным показателем преломления — оптически более плотной.

Пример №4. Определить показатель преломления воды относительно алмаза.

n=nвnа

Абсолютные показатели преломления воды и алмаза — постоянные табличные величины.

n=1,332,42≈0,55

Полное отражение

Закон преломления света позволяет объяснить интересное и практически важное явление — полное отражение света.

При прохождении света из оптически менее плотной среды в более плотную, к примеру, из воздуха в стекло или воду, v1>v2. Следовательно, согласно закону преломления показатель преломления n > 1. Поэтому α > β (см. рисунок а). В результате преломления луч приближается к перпендикуляру, восстановленному к точке падения луча.

Если же направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль ранее преломленного луча (см. рисунок б), то закон преломления запишется следующим образом:

sinαsinβ=v2v1=1n

Преломленный луч по выходе из оптически более плотной среды будет направлен по линии ранее падавшего луча, поэтому α < β, т. е. преломленный луч в этом случае отдаляется от перпендикуляра, восстановленного в точке падения к границе раздела сред. По мере увеличения угла α угол преломления β также увеличивается. При этом, согласно закону преломления света, он всегда будет больше угла α. Наконец, при некотором угле падения α значение угла преломления β приблизится к 90°, и преломленный луч будет направлен почти по границе раздела двух сред (см. рисунок в). Наибольшему возможному углу преломления β = 90° соответствует угол падения α₀.

Попробуем выяснить, что произойдет при α > α₀. При падении света на границу двух сред световой луч, как мы уже говорили ранее, частично отражается и частично преломляется. Но при α > α₀ преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.

Примеры полного отражения света:

блеск от ограненного алмаза;
блеск капель росы на солнце;
внутреннее отражение предметов, находящихся под водой.

Определение

Угол полного отражения — угол падения α₀, соответствующий углу преломления 90°.

При sin β = 1 (что соответствует углу 90°) угол полного отражения можно определить по формуле:

sinα0=1n

Пример №5. Луч света, идущий из толщи воды, полностью отражается от ее поверхности. Выйдет ли луч в воздух, если на поверхность воды налить слой кедрового масла?

Синус угла полного отражения для луча, идущего из воды к воздуху:

sinα0=1n1

sinα0 n1=1

где n1 — показатель преломления воды.

Запишем закон преломления света для случая, когда на поверхность воды налито масло:

Тогда синус угла полного отражения для луча, идущего из воды к маслу:

sinα0sinβ=n2n1

где n2 — показатель преломления масла.

Тогда:

sinβ=1n2

Эта формула соответствует случаю, когда угол β является углом полного отражения. Следовательно, луч света за пределы масляной пленки в воздух не выйдет.

Практическое применение явления полного отражения света

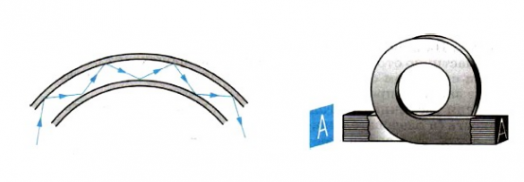
Явление полного отражения света применяют в волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод — это стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления.

За счет многократного полного отражения свет может быть направлен, либо по прямому, либо по изогнутому пути (см. рисунок слева). Волокна собираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (см. рисунок справа). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.

В последнее время волоконная оптика широко используется для быстрой передачи компьютерных сигналов. По волоконному кабелю передается модулированное лазерное излучение.

Задание EF17610

Ученик провёл опыт по преломлению монохроматического света, представленный на фотографии.

Затем вся установка была помещена в воду. Как изменятся частота световой волны, длина волны, падающей на стекло, и угол преломления?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения

1.Описать эксперимент, проведенный учеником.

2.Установить, как изменяется частота световой волны при перемещении установки из воздуха в воду.

3.Установить, как при этом изменяется длина световой волны.

4.Установить, как при этом изменяется угол преломления.

Решение

Ученик направил луч монохроматического света на стекло под углом 30 градусов к нормали. При этом луч вышел под углом 20 градусов. Это говорит о том, что свет из менее плотной оптической среды попал в более плотную.

Частота световой волны — характеристика, не зависящая от условий распространения этой волны. Поэтому при перемещении установки из воздуха в воду частота останется прежней.

Чтобы установить, как меняется длина световой волны и угол преломления. Нужно рассчитать изменение показателя преломления света. Относительный показатель преломления в первом и втором опыте будет соответственно равен:

sinαsinβ=nвоздух−стекло

sinαsinγ=nвода−стекло

Относительные показатели преломления можем выразить через абсолютные:

nвоздух−стекло=nстеклоnвоздух

nвода−стекло=nстеклоnвода

Абсолютный показатель преломления — табличная величина. Мы возьмем приблизительный значения: для воздуха — 1, для воды — 1,33, для стекла — 1,5. В действительности абсолютный показатель преломления стекла может составлять от 1,43 до 2,17. Но это не столь важно, поскольку важно лишь то, что он в любом случае больше абсолютного показателя преломления воды.

Получим:

nвоздух−стекло=1,51=1,5

nвода−стекло=1,51,33≈1,3

Видно, что при перемещении из воздуха показатель преломления уменьшился. Тогда:

sinαsinγ=1,3

Так как числитель в левой части уравнения остался прежним, а число в правой части уменьшилось, то синус угла преломления увеличился. Поскольку синус угла находится в прямой зависимости от величины угла, то и угол преломления увеличился.

Длина волны определяется формулой:

λ=vν

Учтем, что скорость распространения света в более плотной среде уменьшается. Если скорость уменьшилась, то длина воды тоже уменьшилась, поскольку между ними существует прямо пропорциональная зависимость.

Ответ: 321

pазбирался: Алиса Никитина | обсудить разбор

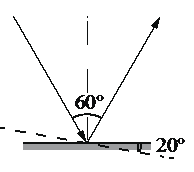
Задание EF18593

Свет падает на горизонтальное плоское зеркало. Угол между падающим и отражённым лучами равен 60°. Каким станет угол между этими лучами, если повернуть зеркало на 20°, как показано на рисунке?

Алгоритм решения

1.Записать известные данные.

2.Зарисовать рисунок после поворота зеркала.

3.Представить решение задачи в общем виде.

4.Подставить неизвестные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Угол между падающим и отраженным углом: γ1 = 60^о.

• Угол поворота угла: φ = 20^о.

Построим рисунок с учетом того, что зеркало повернули:

Поскольку угол падения, равен углу отражения, то:

α1+β1=60°

α1=β1

2α1=60°

α1=60°2=30°

На рисунке видно, что после переворачивания зеркала угол падения α увеличился на угол переворота:

α=α1+φ=30°+20°=50°

Так как угол падения равен углу отражения, то:

α=β=50°

Отсюда угол между лучом падающим и лучом отраженным равен:

γ=α+β=50°+50°=100°

Ответ: 100

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19015

На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.

Алгоритм решения

1.Записать исходные данные.

3.Записать закон полного отражения.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Радиус круглого плота: R = 2,4 м.

• Показатель преломления воды: n = 4/3.

Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.

Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:

sinα=1n

Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.

Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.

Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:

H=Rcotα

Котангенс угла определяется как отношение косинуса этого угла к его синусу:

cotα=cosαsinα

Косинус угла можем выразить из основного тригонометрического тождества:

sin2α+cos2α=1

Следовательно:

cosα=√1−sin2α

Отсюда котангенс равен:

cotα=√1−sin2αsinα

Тогда глубина бассейна:

H=Rcotα=R√1−sin2αsinα

Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:

H=R√1−(1n)21n=Rn√1−1n2

Подставим известные данные и получим:

H=2,4·43⎷1−1(43)2=3,2√1−916=3,2√74≈0,8·2,65=2,12 ⎛⎜⎜⎝м⎞⎟⎟⎠

Ответ: 2,12

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17706

Стеклянную линзу (показатель преломления стекла n_стекла = 1,54), показанную на рисунке, перенесли из воздуха (n_{воздуха} = 1) в воду (n_воды = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?

Ответ:

а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.

б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.

в) Фокусное расстояние и оптическая сила увеличились.

г) Фокусное расстояние и оптическая сила уменьшились.

Алгоритм решения

1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.

2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.

Решение

Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:

nвоздух−стекло=nстеклоnвоздух=1,541=1,54

nвода−стекло=nстеклоnвода=1,541,33≈1,16

Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.

Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.3k

Источник

В (1621) году голландский математик Виллеброрд Снеллиус опытным путём открыл и сформулировал закон преломления света. Он отметил, что при изменении угла падения угол преломления изменяется так, что постоянным остаётся соотношение синусов этих углов.

Закон преломления света (закон Снеллиуса)

Падающий и преломлённый лучи и перпендикуляр, проведённый к границе раздела двух сред в точке падения луча, лежат в одной плоскости.
Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, равная относительному показателю преломления:

Явление полного внутреннего отражения

Рассмотрим луч света, который переходит из среды с большим показателем преломления в вещество с меньшим абсолютным показателем преломления (например, из воды в воздух).

Рис. 1. Схема полного внутреннего отражения

В этом случае угол преломления луча больше, чем угол падения. Если увеличивать угол падения, то при некотором предельном угле

αпр

угол преломления становится равным (90)°. При дальнейшем увеличении угла падения луч полностью отражается от границы раздела и не переходит в другую среду. Это явление называется явлением полного внутреннего отражения (рис. 1).

Запишем закон преломления света для

αпр

Обрати внимание!

Явление полного внутреннего отражения наблюдается только при переходе светового луча из среды с большим абсолютным показателем преломления в среду с меньшим абсолютным показателем преломления вещества, а также при угле падения большем или равным углу

αпр

Явление полного внутреннего отражения используется в волоконной оптике — для передачи световых сигналов на большие расстояния. Использование обычного зеркального отражения не дает желаемого результата, так как даже зеркало самого высокого качества (посеребрённое) поглощает часть световой энергии. И при многократном отражении энергия света стремится к нулю.

Рис. 2. Изображение хода луча в световоде

(1) — защитная оболочка

(2) — оболочка (с меньшим показателем преломления)

(3) — сердцевина (с большим показателем преломления)

Оптическое волокно состоит из внутренней сердцевины, окружающей ее оболочки и дополнительного защитного покрытия (защитной оболочки) (рис. 2). Сердцевина — светопередающая часть волокна из стекла или пластика. Чем больше диаметр сердцевины, тем большее количество света может быть передано по волокну. Оболочка обеспечивает переотражение света в сердцевину волокна таким образом, чтобы световые волны распространялись только по сердцевине волокна. При входе в световод падающий луч направляется под углом больше предельного, что обеспечивает отражение луча без потери энергии. Волоконные световоды с успехом применяют в медицине. Например, световод вводят в желудок или в область сердца для освещения или наблюдения тех или иных участков внутренних органов. Использование световодов позволяет исследовать внутренние органы без введения лампочки, то есть исключая возможность перегрева.

Источник

Отражением светаназываютизменение направления световых лучей
при падении на границу раздела двух
сред, в результате чего свет распространяется
обратно в первую среду.

Угол падения —угол 
между направлением падающего
луча и перпендикуляром к границе раздела
двух сред, восстановленным в точке
падения.

Угол отражения— угол β
между этим перпендикуляром и
направлением отраженного луча.

Законы отражения света:

Луч падающий, перпендикуляр к границе
раздела двух сред в точке падения и луч
отраженный лежат в одной плоскости.
Угол отражения равен углу падения.

Преломлением светаназывают
изменение направления световых лучей
при переходе света из одной прозрачной
среды в другую.

У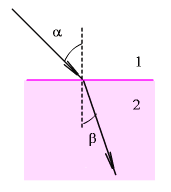гол
преломления— угол 
между тем же перпендикуляром и направлением
преломленного луча.

Скорость света в вакууме с=
3*10⁸ м/с

Скорость света в среде V<c

Абсолютный показатель преломления
средыпоказывает,во сколько раз
скорость света v
в данной среде меньше, чем
скорость света с в вакууме.

Абсолютный показатель преломления для
вакуума равен 1

Скорость света в воздухе очень мало
отличается от значения с,поэтому

Абсолютный показатель преломления для
воздуха будем считать равным
1

Относительный показатель преломленияпоказывает, во сколько раз изменяется
скорость света при переходе луча из
первой среды во вторую.

Законы преломления света:

Луч падающий, перпендикуляр к границе
раздела двух сред в точке падения и
преломленный луч лежат в одной плоскости.
Отношение синуса угла падения 
к синусу угла преломления 
есть величина постоянная для
данной пары сред:

где V₁
и V₂–
скорости распространения света в первой
и второй среде.

Сучетом показателя преломления закон
преломления света можно записать в виде

или

где n₂₁–
относительный показатель
преломления второй среды
относительно первой;

n₂ и n₁
– абсолютные показатели
преломления второй и первой
среды соответственно

Полное внутреннее отражение

Если световые лучи из оптически более
плотной среды 1 падают на границу
раздела с оптически менее плотной
средой 2 (n₁n₂),то угол падения
меньше угла преломления 
 .
При увеличении угла падения можно
подойти к такому его значению _пр,
когда преломленный луч заскользит по
границе раздела двух сред и не попадет
во вторую среду,

Угол преломления ,
при этомвся световая энергия отражается
от границы раздела.

Предельным углом полного внутреннего
отражения _прназывается угол, при котором преломленный
луч скользит вдоль поверхности двух
сред,

При переходе
из среды оптически менее плотной в
среду более плотную полное внутреннее
отражение невозможно.

43 Интерференция света. Дифракция света. Дифракционная решетка.

Интерференция света

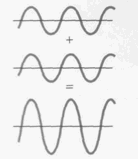
Интерференциейволн называетсяявление увеличения или уменьшения
амплитуды результирующей волны при
сложении волн с одинаковой частотой
колебаний и постоянной во времени
разностью фаз.

В точках, где амплитуда колебаний
увеличивается, наблюдается
интерференционный максимум

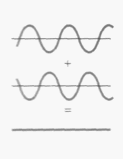
В точках, где амплитуда колебаний

уменьшается, наблюдается

интерференционный минимум

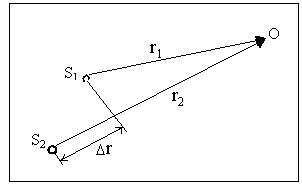
Волны и возбуждающие их источники
называются когерентными, еслиразность фаз волн не зависит от времени,
и волны имеют одинаковую длину волны.
Результат наложения когерентных световых
волн, наблюдаемый на экране, фотопластинке
и т.д., называется интерференционной
картинкой. Устойчивую
интерференционную картину дают только
когерентные волны.

Волны от естественных источников не
бывают когерентными, поэтому для
наблюдения интерференции света
искусственно создают разность хода
световых волн, разделяя свет

от одного источника на два пучка,
которые проходят разные пути r₁
и r₂,
а затем эти пучки сводятся вместе на
экране.

 — длина волны,

r= r₂
–r₁–геометрическая разность хода двух

волн

Δφ – разность фаз волн

Δφ=2πr/

Геометрической разностью хода
называется разница расстояний,
пройденных волнами от разных источников
до точки, где наблюдается их интерференция

Условие интерференционных максимумов
(усиление света)

Для
разности фаз

Δφ= 2πk— разность
фаз кратна 2π

для разности хода

r = k
или

r = 2k

k-любое целое
число(k
=0,1,2,3, …),

Разность хода равна четному числу
полуволн

Условие интерференционных минимумов
(ослабление света):

Для разности фаз

Δφ=
π(2k+1)

для разности хода

r = (2k
+ 1) ,

где k –
целое число (k
=0,1,2,3, …),

Разность хода равна нечетному числу
полуволн

Дифракцией света называется
отклонение направления распространения
волн от прямолинейного у границы
преграды.

Наиболее наглядно дифракция света
проявляется при прохождении света через
отверстия с размерами порядка длины
волн оптического диапазона. Явление
дифракции легко наблюдать на дифракционной
решетке.

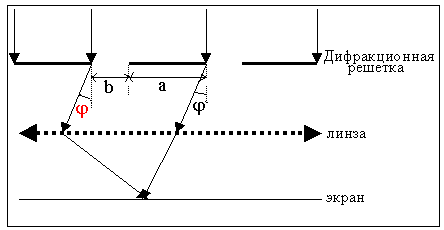
Простейшей дифракционной решеткой
является система из N
одинаковых параллельных щелей в плоском
непрозрачном экране ширины b
каждая, расположенных на равных
непрозрачных промежутках a
друг от друга. Величина d
= b + a
называется постоянной (периодом)
дифракционной решетки.

Прохождение монохроматического
излучения через дифракционную решетку

Монохроматическим называется излучение,
состав которого определяется одной
длиной волны. Например, волна с длиной
волны λ = 770 нм – монохроматический
красный свет.

φ- угол дифракции

Лучи, прошедшие дифракционную решетку,
когерентны, поэтому дают на экране
интерференционную картину.

Для двух лучей, испытывающих дифракцию
на краях двух соседних щелей, геометрическая
разность хода r
= dsin

Положение главных максимумов освещенности
в дифракционной картинке, получаемой
при нормальном падении световой волны
на поверхность решетки, определяется
соотношением:

d sin=
k

где d sin—разность хода лучей световых волн
от соседних щелей;—угол дифракции, т.е. угол между
направлением хода падающей на решетку
световой волны и направлением хода
волны на выходе ее из щели; k
– порядок максимума (k
= 0,1,2,3,…).

Положения главных минимумов определяется
соотношением

d sin=
(2k + 1) ,

k – порядок
минимума (k =
0,1,2,3,…).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
13.02.201521.66 Mб28Bammes_Der_Nackte_Mensch.pdf
#
#
#
#
#
#

Источник