Как найти синус угла при основании треугольника

Я так понял, что задача сводится к тому, что нам неизвестен угол треугольника, и нам нужно его найти.

Для того чтобы найти синус угла, а затем и сам угол в произвольном треугольнике, необходимо знать длины двух сторон: стороны, противолежащей искомому углу, и какой-либо другой стороны — и ещё величину угла, противолежащего этой последней стороне.

А затем нужно применить теорему синусов.

Обозначим искомый (неизвестный) угол как A, противолежащую сторону — a, другую известную сторону — b, известный противолежащий этой стороне угол — B.

По теореме синусов: a/sin(A) = b/sin(B).

Отсюда: sin(A) = a * sin(B)/b;

A = arcsin[a * sin(B)/b].

Как найти синус угла в равнобедренном треугольнике

Равнобедренным треугольником называется выпуклая геометрическая фигура из трех вершин и трех соединяющих их отрезков, два из которых имеют одинаковую длину. А синус — это тригонометрическая функция, которую можно использовать для численного выражения зависимости между соотношением длин сторон и величинами углов во всех треугольниках, включая и равнобедренные.

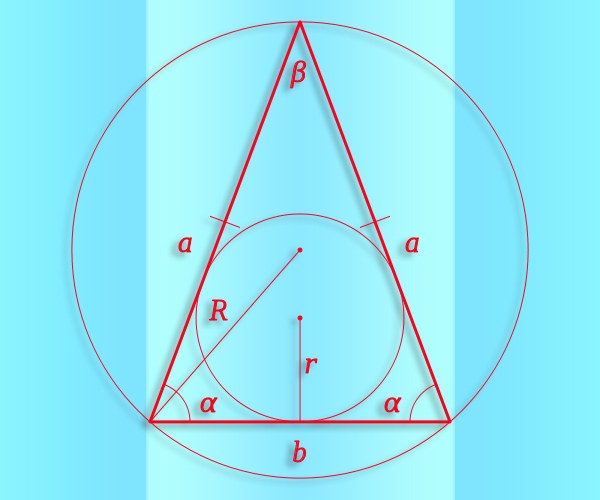
Инструкция

Если из исходных данных известна величина хотя бы одного угла (α) в равнобедренном треугольнике, это позволит найти и два других (β и γ), а значит и синус любого из них. Исходите из теоремы о сумме углов, которая утверждает, что в треугольнике она обязательно должна быть равна 180°. Если угол известной величины лежит между боковыми сторонами, величина каждого из двух других равна половине разности между 180° и известным углом. Значит, вы можете использовать в расчетах такое тождество: sin(β) = sin(γ) = sin((180°-α)/2). Если же известный угол примыкает к основанию треугольника, это тождество распадется на два равенства: sin(β) = sin(α) и sin(γ) = sin(180°-2*α).

Зная радиус (R) окружности, описанной около такого треугольника, и длину любой из сторон (например, а) можно не прибегая к вычислению тригонометрических функций рассчитать синус угла (α), лежащего напротив этой стороны. Используйте для этого теорему синусов — из нее вытекает, что нужная вам величина равна половине соотношения между длиной стороны и радиусом: sin(α) = ½*R/a.

Известные площадь (S) и длина боковой стороны (а) равнобедренного треугольника позволят рассчитать синус угла (β), лежащего напротив основания фигуры. Для этого удвойте площадь и поделите результат на возведенную в квадрат длину боковой стороны: sin(β) = 2*S/a². Если кроме длины боковой стороны известна и длина основания (b), квадрат можно заменить произведением длин этих двух сторон: sin(β) = 2*S/(a*b).

Если известны длины боковой стороны (а) и основания (b) равнобедренного треугольника, для вычисления синуса угла при основании (α) можно задействовать даже теорему косинусов. Из нее вытекает, что косинус этого угла равен половине отношения длины основания к длине боковой стороны: cos(α) = ½*b/a. Синус и косинус связаны таким равенством: sin²(α) = 1-cos²(α). Поэтому для вычисления синуса извлеките квадратный корень из разницы между единицей и четвертью соотношения квадратов длин основания и боковой стороны: sin(α) = √(1-cos2(α)) = √(1-¼*b²/а²).

Источники:

• рассчитать синус

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Синус в треугольнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция — arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

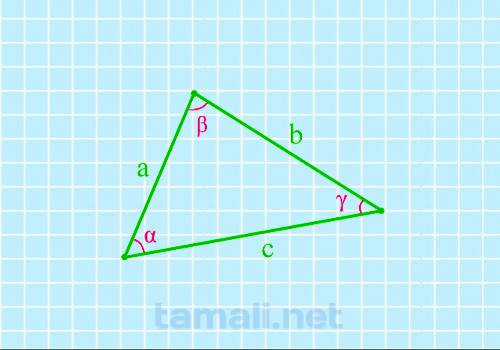
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

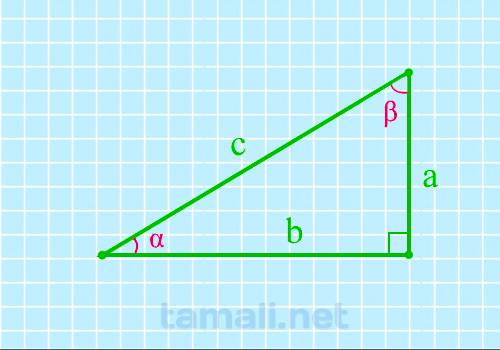
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

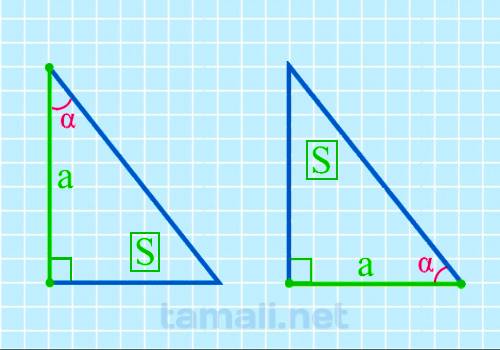
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

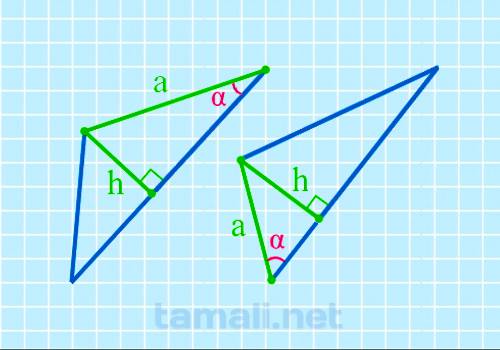
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

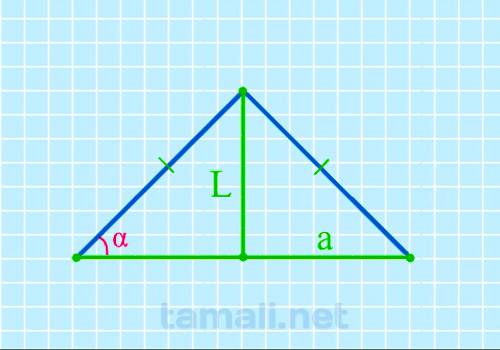
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

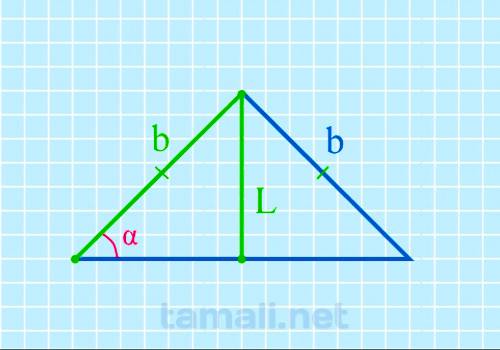
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

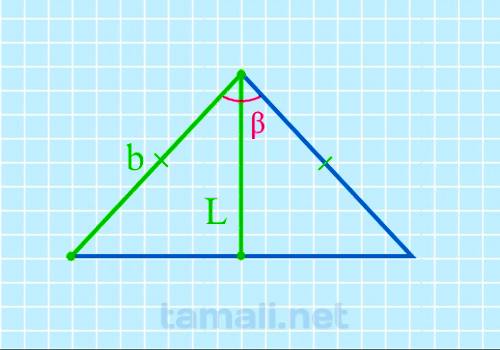
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

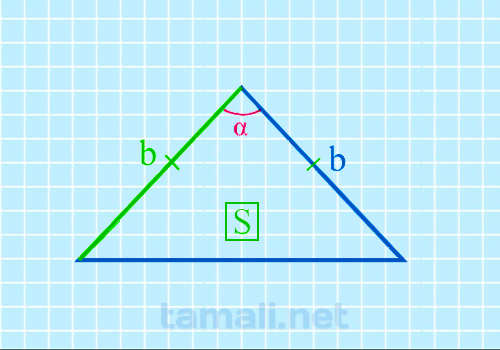
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin	sincos
cos	1+tg	cos = sin
tg	1+ctg	sin = cos
ctg		tg = ctg

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на получаем то есть
   Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

	0
sin	0
cos					0
tg	0				−
ctg	−				0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому

Из этих равенств следует, что т. е. sin А = sin

Аналогично, т. е. cos А = cos и т. е. tg A = tg

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку , sin A = cos B = 0,1.

Задача 2. В треугольнике угол равен , , .

Найдите .

Решение:

Отсюда

Найдем AC по теореме Пифагора.

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A

Катет, прилежащий к – это катет АС, следовательно, cos⁡ А

Длину катета АС найдем по теореме Пифагора:

Тогда

cos⁡ А

tg A

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A

По теореме Пифагора получим

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен tg A = Найдите AB.

Решение:

AC = b = 4, tg A

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = Найдите AH.

Решение:

AВ = с = 13, tg A = тогда b = 5a.

По теореме Пифагора ABC:

тогда

(по двум углам), следовательно откуда

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A =

Найдите AH.

Решение:

Так как sin A = тогда c = АВ = 18.

sin A = = cos⁡ B =

Рассмотрим BHC:

= получим

тогда BH = = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =

Найдите АH.

Решение:

Так как для АВС: A = sin В =

а для ВНС: sin В = = , откуда СН =

По теореме Пифагора найдем ВН:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

тогда

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= = =

Рассмотрим BHC :

ВС найдем по теореме Пифагора:

ВС=

тогда а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = = = cos A = = =

тогда tg A = который найдем из BHC:

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A = Найдите АН.

Решение:

По определению tg A=

Для BHC: , значит СН =

Для АHC: tg A= то AH =

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A = Найдите АВ.

Решение:

Так как cos В = = sin A =

Из СВН имеем cos В = = тогда ВС =

В АВС имеем sinA = = тогда AВ =

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

sin В = =

Для АВС: cos A = получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора получим

х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит или

k = тогда АС = ; АВ =

3-й способ.

(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

=

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = =

cos C =

Для АВС: sin А = = cos C =

Для АНВ: sin А = = то = АВ =

Из основного тригонометрического тождества найдем

cos A =

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А =

значит = 14.

Второй катет найдем, используя теорему Пифагора:

Площадь прямоугольного треугольника равна S =

поэтому

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, ),

значит sin

Найдем АС по теореме Пифагора из САВ:

Тогда sin

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ =

Поскольку АСН — прямоугольный,

cos A = то есть АС =

По теореме Пифагора тогда

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 sin A = AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора

(14х- 11х)(14х + 11х) = 3 100;

учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством

cos A =

По определению cos A = значит

Так как АС=10 то откуда АВ = = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.

Решение:

Пусть ВАО =

Диагонали ромба делят его углы пополам, значит, =

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =

Поэтому tg откуда

Ответ:

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 угол А равен 30 АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла имеем ВС = АВ =

В BHC: то следовательно, ВН = BC =

По теореме Пифагора найдем НС:

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 CH — высота, АВ = 2, Найдите АH.

Решение:

Из АВС найдем ВС = АВ = 1 (по свойству катета, лежащего против угла 30),

то

Из ВСН: то следовательно,

ВН = ВС =

АН = АВ — НВ = 2 — = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн