Учебник
Геометрия, 9 класс
Формулы площадей через синус угла
Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков — равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- Площадь прямоугольника равна произведению ширины на длину … произведение сторон.
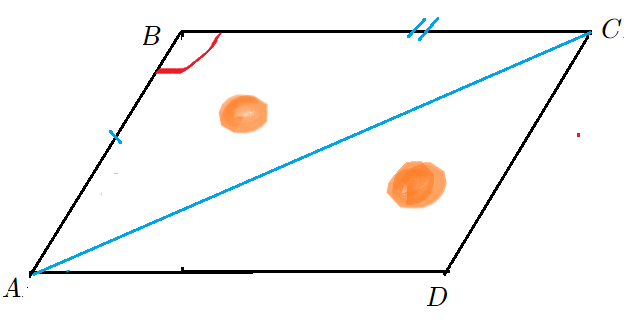
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $frac{1}{2}$. Найти площадь параллелограмма.
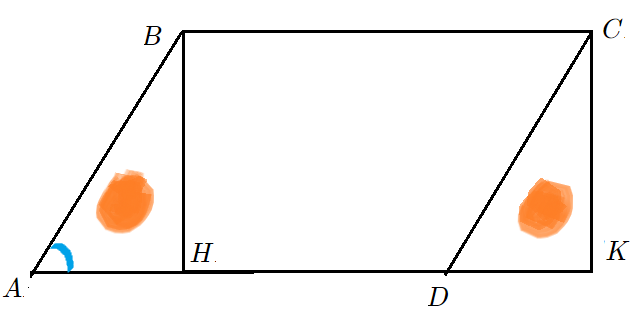
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут «увидеть» площадь.
- Что есть синус $angle BAH$ в прямоугольном треугольнике $bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь — сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $bigtriangleup DCK$. Площадь также «сумма кусков».
- Треугольники $bigtriangleup ABH$ и $bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BHcdot HK=ABcdotsin angle BADcdot AD=7cdotfrac{1}{2}cdot10$
Теорема «о площади параллелограмма и треугольника через синус угла»:
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=acdot bcdotsin angle BAD$ $S_{ABCD}=ABcdot BCcdotsin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=frac{1}{2}cdot acdot bcdotsin angle C$ $S_{bigtriangleup ABC}=frac{1}{2}cdot ABcdot BCcdotsin angle CBA$
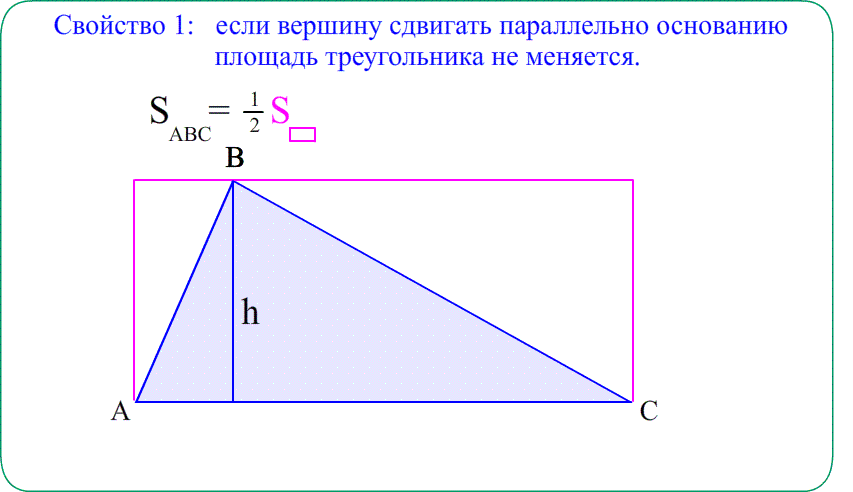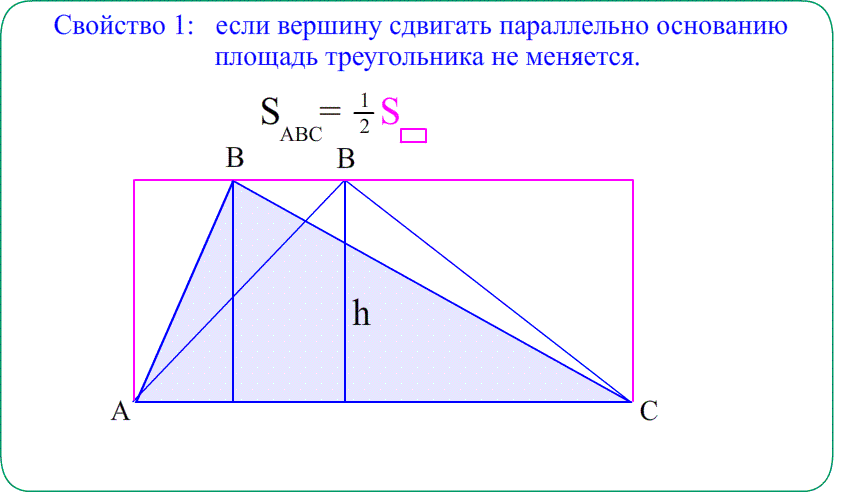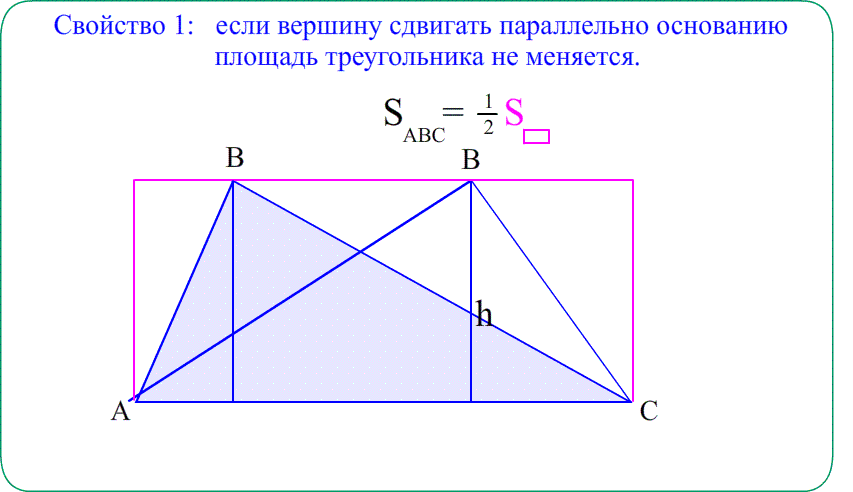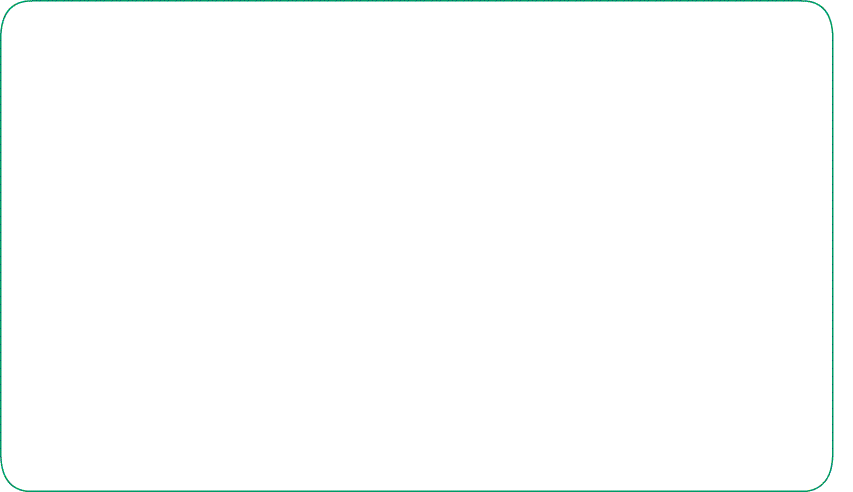
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ … угол между $sinangle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{bigtriangleup AOB}+S_{bigtriangleup BOC}+S_{bigtriangleup COD}+S_{bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{bigtriangleup AOB}=frac{1}{2}cdot AOcdot OBcdot sin angle AOB=frac{1}{2}cdot 7 cdot 3cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $sinangle BOC=sinangle COD=sinangle AOD=0,2$
- Тогда, площади других треугольников $frac{1}{2}cdot 3 cdot 6cdot 0,2=1,8$ $frac{1}{2}cdot 6 cdot 5cdot 0,2=3$ $frac{1}{2}cdot 5 cdot 7cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $frac{1}{2}cdot OAcdot OBcdot sin angle AOB+frac{1}{2}cdot OBcdot OCcdot sin angle AOB+frac{1}{2}cdot OCcdot ODcdot sin angle AOB+frac{1}{2}cdot ODcdot OAcdot sin angle AOB$
- Вынос за скобки множителей $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OAcdot OB+OBcdot OC+OCcdot OD+ODcdot OAright)$
- $S_{ABCD}=frac{1}{2}cdot sin angle AOBcdot left(OBcdotleft(OA+OCright)+ODcdotleft(OA+OCright)right)=frac{1}{2}cdot sin angle AOBcdot AC cdot (OB+OD)$
- Получаем $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$ $Rightarrow$ $S_{ABCD}=frac{1}{2}cdot (7+6) cdot (3+5)cdot 0,2=13cdot 0,8=10,4$

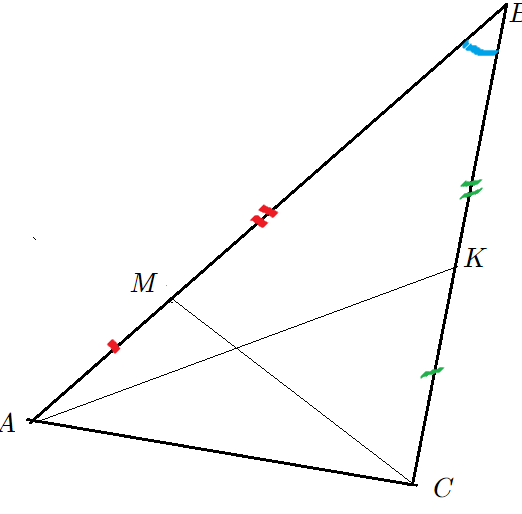
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$, $angle ABC=30$. Найти: $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $frac{x}{y}=?$ $x+y=?$
- $frac{AM}{MB}=frac{3}{5}$, аддитивность $AM+MB=AB=10$ $Rightarrow$ $frac{AM}{AB}=frac{3}{3+5}$ $Rightarrow$ $AM=frac{15}{4}$, $MB=frac{25}{4}$
- $frac{BK}{KC}=frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=frac{24}{5}$, $KC=frac{36}{5}$
- Найдем площадь через синус $S_{bigtriangleup ABK}=frac{1}{2}cdot AB cdot BK cdot sin angle ABC = frac{1}{2}cdot 10 cdot frac{24}{5} cdot sin 30= 24 cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{bigtriangleup MBC}=frac{1}{2}cdot MB cdot BC cdot sin angle ABC = frac{1}{2}cdot frac{25}{4} cdot 12 cdot 0,5=frac{75}{4}$
- отношение площадей треугольников $frac{S_{bigtriangleup ABK}}{S_{bigtriangleup MBC}}=frac{12}{frac{75}{4}}=frac{16}{25}$ Ответ: $frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $frac{AM}{MB}=frac{3}{5}$, $frac{BK}{KC}=frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{bigtriangleup ABK}$ , $S_{bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
Теорема «о площади четырехугольника через диагонали и синус угла»:
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2 cdotsin angle alpha$ $S_{ABCD}=frac{1}{2}cdot AC cdot BDcdot sin angle AOB$
- Площадь ромба равна половине произведения диагоналей. … диагонали перпендикулярны!
- Формулы $S=frac{1}{2}cdot d_1 cdot d_2=frac{1}{2}cdot AC cdot BD$ $angle AOB=90$ $sin angle AOB=1$
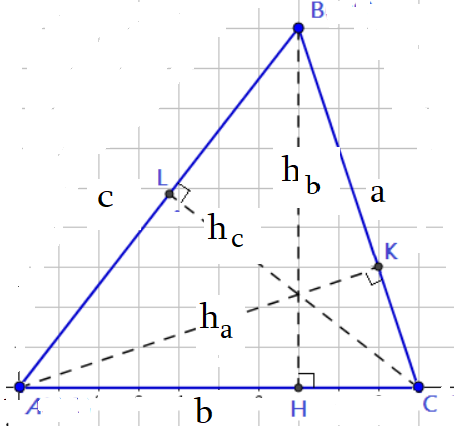
Формулы площади треугольника:
$S=frac{acdot h_a}{2}=frac{acdot bcdotsin C}{2}$ $S=frac{bcdot h_b}{2}=frac{bcdot ccdotsin A}{2}$ $S=frac{ccdot h_c}{2}=frac{ccdot acdotsin B}{2}$.
$sin A=frac{h_b}{c}=frac{h_c}{b}$ $sin B=frac{h_a}{c}=frac{h_c}{a}$ $sin C=frac{h_b}{a}=frac{h_a}{b}$.
$S_{ABC}=frac{1}{2}cdot ACcdot BCcdotsin C$ $S_{ABC}=frac{1}{2}cdot ABcdot BCcdotsin B$ $S_{ABC}=frac{1}{2}cdot ACcdot ABcdotsin A$ .
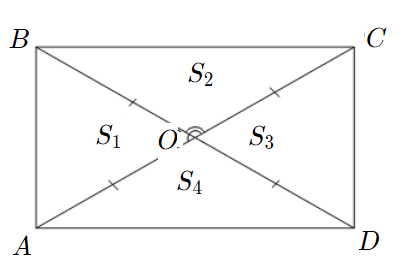
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ — прямоугольник , $AC=10$ , $angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
- $bigtriangleup AOB$ и $bigtriangleup COD$ равные $Rightarrow$ $S_1=S_3$ ;
- $bigtriangleup BOC$ и $bigtriangleup AOD$ равные $Rightarrow$ $S_2=S_4$ .
- Смежные, $angle BOC=180-angle AOB=150$. Найдем отношение $frac{S_1}{S_2}=frac{frac{1}{2}AOcdot OBcdotsin30}{frac{1}{2}BOcdot OCcdotsin150}$
- $sin30=sinleft(180-30right)=sin150$. тогда $frac{S_1}{S_2}=frac{frac{1}{2}cdot5cdot5cdotsin150}{frac{1}{2}cdot5cdot5cdotsin150}=1$ Значит, $S_1=S_2$
- Аналогично: $frac{S_3}{S_4}=frac{frac{1}{2}DOcdot OCcdotsin30}{frac{1}{2}AOcdot ODcdotsin150} =1$ $Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- … тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=frac{1}{2}AOcdot OBcdot sin 30=frac{1}{2}cdot 5cdot 5cdot frac{1}{2}=frac{25}{4}$ $Rightarrow$ $S_{ABCD}=4cdotfrac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Одинаковый «состав» углов. Все прямоугольные,
- Прямоугольный $bigtriangleup BED$, по Пифагору выразим катет $DE=sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=frac{BD}{2}=6,5$ $AO=frac{AC}{2}$ $AC=2cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $bigtriangleup BED sim bigtriangleup AOD$ $Rightarrow$ $frac{AO}{BE}=frac{OD}{ED}$ $Rightarrow$ $AO=frac{ODcdot BE}{ED}=frac{6,5cdot 12}{5}=15,6$ $AC=2cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=frac{1}{2}cdot ACcdot BD=0,5cdot 31,2cdot13=202,8$

Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=frac{1}{2}acdot acdotsin30$ , тогда $100=frac{1}{2}a^2cdotsin30$ $Leftrightarrow$ $100=frac{1}{2}a^2cdotfrac{1}{2}$ $Rightarrow$
- $a=sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=sqrt{a^2+a^2-2cdot acdot acdotfrac{sqrt{3}}{2}}=asqrt{2-sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $sin15=frac{0,5cdot c}{a}=frac{0,5cdot acdotsqrt{2-sqrt{3}}}{a}=frac{sqrt{2-sqrt{3}}}{2}$
- Площадь через основание $S=frac{1}{2}cdot ccdot h$, найдем высоту $h=frac{2cdot S}{c}=frac{2cdot0,5cdot a^2cdotsin30}{acdotsqrt{2-sqrt{3}}}=frac{a}{2cdotsqrt{2-sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $frac{c}{2}$, $a$. Тогда $cos15=frac{h}{a}=frac{frac{a}{2cdotsqrt{2-sqrt{3}}}}{a}=frac{1}{2cdotsqrt{2-sqrt{3}}}$
Интерактивные Упражнения
Синус в квадрате
Синус (sin) — это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
sin 2 (x)=sin(x)*sin(x)
Значение синуса находится в диапазоне от -1 до +1.
Смотрите также калькулятор вычисления синуса угла.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Площадь прямоугольника через диагональ
В прямоугольнике диагонали равны между собой. Если известен угол α между диагоналями (длина диагоналей равна d), то площадь прямоугольника можно найти по формуле:
Sпр = 0,5 * d² * sinα.
Например, если угол между диагоналями равен 30°, а диагонали равны 5 см, то площадь будет равна:
Sпр = 0,5 * 25 * 0,5 = 6,25 см.
Если неизвестен угол между диагоналями, то будет нужно найти стороны прямоугольника. А затем воспользоваться формулой:
Sпр = a * b.
Как известно, диагональ прямоугольника делит его на 2 равных прямоугольных треугольника. Поэтому задача сводится к тому, чтобы найти катеты прямоугольного треугольника через гипотенузу.
Кроме длины диагонали требуется знать либо одну из сторон прямоугольника, либо отношение сторон, либо угол между стороной и диагональю.
1) Если известна диагональ (пусть она будет равна d) и одна из сторон (например, b), то выражаем неизвестную сторону из формулы:
a² + b² = c² -> a = √(c² — b²).
Sпр = a * b = √(c² — b²) * b.
Например, если диагональ d = 5 см и сторона b = 3 см, то a = √(25 — 9) = √16 = 4 см.
Площадь прямоугольника равна 3 * 4 = 12 см.
2) Если известно отношение сторон, то задача сводится к нахождению обеих сторон через составление уравнения.
Например, если стороны относятся как 2:3, а диагональ равна 13 см, то можно составить уравнение:
(2x)² + (3x)² = 4x² + 9x² = 169.
13x² = 169.
x = √13.
Значит, a = 2√13 см и b = 3√13 см.
Площадь прямоугольника равна 2√13 * 3√13 = 6 * 13 = 78 см.
3) Если известна диагональ и один из прилежащих к диагонали углов, то нужно воспользоваться формулами:
a = d * cosβ (β — прилежащий угол) и b = d * sinα (α — противолежащий угол).
Например, d = 10 см и угол α = 30°.
a = 10 * cos30° = 10√3 / 3.
b = 10 * sin30° = 5 см.
Площадь прямоугольника равна 5 * (10√3 / 3) ≈ 28,33 см.
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
— это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Ниже представлены таблицы с формулами степеней (квадрат, куб, в 4-ой степени) прямых и обратных тригонометрических функций: синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы понижения степени тригонометрических функций
Формулы понижения степени являются одним из видов основных тригонометрических формул. Они выражают степени (2, 3, …) тригонометрических функций синус, косинус, тангенс, котангенс через синус и косинус первой степени, но кратного угла (`alpha, 3alpha, …` или `2alpha, 4alpha, …`).
Содержание статьи:
Список всех тригонометрических формул понижения степени
Запишем данные тождества для тригонометрических функций от 2-й по 4-ю степень угла `alpha`, а также для угла `frac alpha 2` и для произведения синус на косинус. Для удобства разделим их на группы.
Для квадрата
Формулы этой группы, особенно две первые, наиболее нужны. Они применяются при решении тригонометрических уравнений, интегралов и т. д.
`sin^2 alpha=frac{1-cos 2alpha}2`
`cos^2 alpha=frac{1+cos 2alpha}2`
`tg^2 alpha=frac{1-cos 2alpha}{1+cos 2alpha}`
`ctg^2 alpha=frac{1+cos 2alpha}{1-cos 2alpha}`
Для куба
Тождества этой группы и следующих встречаются гораздо реже, но это не повод их не знать.
`sin^3 alpha=frac{3sin alpha-sin 3alpha}4`
`cos^3 alpha=frac{3cos alpha+cos 3alpha}4`
`tg^3 alpha=frac{3sin alpha-sin 3alpha}{3cos alpha+cos 3alpha}`
`ctg^3 alpha=frac{3sin alpha+sin 3alpha}{3cos alpha-cos 3alpha}`
Для 4-й степени
`sin^4 alpha=frac{3-4cos 2alpha+cos 4alpha}8`
`cos^4 alpha=frac{3+4cos 2alpha+cos 4alpha}8`
Для функций половинного угла
Это формулы половинного угла. Но когда они записаны именно в таком виде, то их можно отнести и к тодествам понижения степени.
` sin^2 frac alpha 2=frac{1-cos alpha}2`
` cos^2 frac alpha 2=frac{1+cos alpha}2`
`tg^2 frac alpha 2=frac{1-cos alpha}{1+cos alpha}`
`ctg^2 frac alpha 2=frac{1+cos alpha}{1-cos alpha}`
Для произведения синус на косинус
`sin^2 alpha cdot cos^2 alpha=frac{1-cos 4alpha}8`
`sin^3 alpha cdot cos^3 alpha=frac{3sin 2alpha-sin 6alpha}32`
`sin^4 alpha cdot cos^4 alpha=frac{3-4cos 4alpha+cos 8alpha}128`
`sin^5 alpha cdot cos^5 alpha=frac{10sin 2alpha-5sin 6alpha+sin 10alpha}512`
Доказательство
Теперь перейдем непосредственно к выводу формул понижения степени тригонометрических функций.
Чтобы доказать их для квадрата, нам понадобятся фождества двойного угла `cos 2alpha=1-2 sin^2 alpha` и `cos 2alpha=2 cos^2 alpha-1`.
Формулу понижения степени синуса в квадрате получим, разрешив первое равенство относительно ` sin^2 alpha`: `sin^2 alpha=frac{1-cos 2alpha}2`.
Аналогично и с косинусом в квадрате, получим тождество, разрешив второе равенство относительно ` cos^2 alpha`: `cos^2 alpha=frac{1+cos 2alpha}2`.
Формула понижения степени тангенса и котангенса автоматически выводится из определений этих функций. Поскольку `tg alpha=frac {sin alpha}{cos alpha}`, то `tg^2 alpha=frac {sin^2 alpha}{cos^2 alpha}=` `frac {frac{1-cos 2alpha}2}{frac{1+cos 2alpha}2}=frac{1-cos 2alpha}{1+cos 2alpha}`. Аналогично получим `ctg^2 alpha=frac {cos^2 alpha}{sin^2 alpha}=` `frac {frac{1+cos 2alpha}2}{frac{1-cos 2alpha}2}=frac{1+cos 2alpha}{1-cos 2alpha}`.
Для лучшего усвоения теоретического материала рекомендуем посмотреть видео, где подробно описывается процесс доказательстве первых двух формул:
Если формулы тройного угла `sin 3alpha=3 sin alpha-4sin^3 alpha` и
`cos 3alpha=4cos^3 alpha-3 cos alpha` разрешить относительно `sin 3alpha` и `cos 3alpha`, то получим формулы понижения степени для синуса и косинуса в кубе: `sin^3 alpha=frac{3sin alpha-sin 3alpha}4` и `cos^3 alpha=frac{3cos alpha+cos 3alpha}4`.
Доказать данной равности для синуса и косинуса можно, воспользовавшись два раза формулами понижения квадратов:
`sin^4 alpha=(sin^2 alpha)^2=(frac{1-cos 2alpha}2)^2=` `frac{1-2cos 2alpha+cos^2 2alpha}4=frac{1-2cos 2alpha+frac{1+cos 4alpha}2}4=` `frac{3-4cos 2alpha+cos 4alpha}8`;
`cos^4 alpha=(cos^2 alpha)^2=(frac{1+cos 2alpha}2)^2=` `frac{1+2cos 2alpha+cos^2 2alpha}4=frac{1+2cos 2alpha+frac{1+cos 4alpha}2}4=` `frac{3+4cos 2alpha+cos 4alpha}8`.
Общий вид формул понижения степени
Для четных показателей степени (n=1, 2, 3,…):
`sin^n alpha=frac {C_frac n 2^n}{2^n}+frac1{2^{n-1}} cdot sum_{k=0}^{frac n 2 -1} (-1)^{frac n 2 -k} cdot C_k^n cdot cos((n-2k) alpha)` и `cos^n alpha=frac {C_frac n 2^n}{2^n}+frac1{2^{n-1}} cdot sum_{k=0}^{frac n 2 -1} C_k^n cdot cos((n-2k) alpha)`.
Для нечетных показателей степени (n=3, 5, 7,…):
`sin^n alpha=frac1{2^{n-1}} cdot sum_{k=0}^{frac {n-1}2} (-1)^{frac {n-1} 2 -k} cdot C_k^n cdot sin((n-2k) alpha)` и `cos^n alpha=frac1{2^{n-1}} cdot sum_{k=0}^{frac {n-1}2} C_k^n cdot cos((n-2k) alpha)`.
Примеры решения задач с применением формул понижения степени
Пример 1. Воспользуйтесь формулой понижения степени для `cos^2 4alpha`.
Решение. Применив формулу `cos^2 alpha=frac{1+cos 2alpha}2`, получим `cos^2 4alpha=frac{1+cos 2cdot 4alpha}2=frac{1+cos 8alpha}2`.
Ответ. `cos^2 4alpha=frac{1+cos 8alpha}2`.
Пример 2. Используя выше указанные тождества, вычислить `sin^2 frac pi 8`.
Решение. Согласно формуле `sin^2 alpha=frac{1-cos 2alpha}2`, понизим степень синуса. Получим `sin^2 frac pi 8=frac{1-cos 2frac pi 8}2=frac{1-cos frac pi 4}2`. Поскольку `cos frac pi 4=frac {sqrt 2}2`, то `sin^2 frac pi 8=frac{1-cos frac pi 4}2=frac{1-frac {sqrt 2}2}2=frac{frac {2-sqrt 2}2}2=frac {2-sqrt 2}4`.
Ответ. `sin^2 frac pi 8=frac {2-sqrt 2}4`.
Отметим, что формулы понижения степени в тригонометрии чаще всего используются при решении уравнений и преобразовании выражений.
Материалы по теме:
Поделиться с друзьями:

Квадрат — синус — Большая Энциклопедия Нефти и Газа, статья, страница 1
Квадрат — синус
Cтраница 1
Квадраты синусов определяют на выходе вторую гармонику.
[1]
Преобразуя квадрат синуса, находим.
[2]
Сумма квадратов синуса и косинуса одного угла равна единице.
[3]
Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине.
[4]
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
[5]
Для исследования суммы квадратов синусов этих углов воспользуйтесь теоремой косинусов.
[6]
Доказать, что сумма квадратов синусов трех углов, образуемых произвольным лучом с ребрами прямого трехгранного угла, равна двум.
[7]
Так как в выражении (5.21) присутствует квадрат синуса, то мгновенная мощность всегда является положительной величиной. Положительный знак мгновенной мощности отражает тот факт, что происходит, односторонний процесс поглощения энергии в цепи переменного тока.
[9]
Эту теорему можно сформулировать так: квадрат синуса любого угла плюс квадрат косинуса того же угла равен единице.
[10]
Для получения подобного ряда следует взять отношения квадрата синуса 6 — каждой из линий Кка дифракционной картины рент-генограммы к квадрату синуса 9i первой линии.
[11]
Для получения подобного ряда следует взять отношения квадрата синуса в — каждой из линий ХЛа дифракционной картины рентгенограммы к квадрату синуса 0Г первой линии.
[13]
Формула или закон, известный обычно как закон квадрата синуса сопротивления воздуха Ньютона, относится к силе, действующей на наклонную плоскую пластину, омываемую равномерным воздушным потоком.
[14]
Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла.
[15]
Страницы:
1
2
3
4
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
1. Формула стороны квадрата через диагональ
a — сторона квадрата
d — диагональ квадрата
Формула стороны квадрата, (a):
2. Формула стороны квадрата через радиус вписанной окружности
a — сторона квадрата
R — радиус вписанной окружности
D — диаметр вписанной окружности
Формула стороны квадрата, (a):
3. Формула стороны квадрата через радиус описанной окружности
a — сторона квадрата
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула стороны квадрата, (a):
4. Формула стороны квадрата через площадь и периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
Формула стороны квадрата, (a):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a — сторона квадрата
C — линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
d — диагональ прямоугольника
a, b — стороны
α, β — углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
Формулы диагонали через сторону и угол, (d):
Формулы величины углов через диагональ и стороны, (α, β):
2. Формулы углов между диагоналями в прямоугольнике.
d — диагонали прямоугольника
a, b — стороны
α, β — углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):
1. Формулы диагонали квадрата через стороны, площадь, периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
d — диагональ квадрата
Формулы диагонали квадрата, (d ):
2. Формула диагонали квадрата через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
d — диагональ квадрата
Формула диагонали квадрата, (d ):
3. Формула диагонали квадрата через радиус описанной окружности
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула диагонали квадрата, (d ):
4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата
C — линия выходящая из угла на середину стороны квадрата
d — диагональ
Формула диагонали квадрата, (d ):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
|
02=0 12=1 22=4 32=9 42=16 52=25 62=36 72=49 82=64 92=81 |
102=100 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 |
202=400 212=441 222=484 232=529 242=576 252=625 262=676 272=729 282=784 292=841 |
302=900 312=961 322=1024 332=1089 342=1156 352=1225 362=1296 372=1369 382=1444 392=1521 |
402=1600 412=1681 422=1764 432=1849 442=1936 452=2025 462=2116 472=2209 482=2304 492=2401 |
|
502=2500 512=2601 522=2704 532=2809 542=2916 552=3025 562=3136 572=3249 582=3364 592=3481 |
602=3600 612=3721 622=3844 632=3969 642=4096 652=4225 662=4356 672=4489 682=4624 692=4761 |
702=4900 712=5041 722=5184 732=5329 742=5476 752=5625 762=5776 772=5929 782=6084 792=6241 |
802=6400 812=6561 822=6724 832=6889 842=7056 852=7225 862=7396 872=7569 882=7744 892=7921 |
902=8100 912=8281 922=8464 932=8649 942=8836 952=9025 962=9216 972=9409 982=9604 992=9801 |
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
62 = 6 × 6 = 36
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».
Скачать таблицу квадратов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
Косинус в квадрате, формула и примеры
ОПРЕДЕЛЕНИЕ
Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2
| Задание | Упростить выражение |
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом: и Тогда Полученное выражение представляет собой правую часть формулы произведения синусов, т.е. |
| Ответ |
| Понравился сайт? Расскажи друзьям! | |
Синусоидальная функция — исчисление
Эта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена информация о функции, включая ее область, диапазон и ключевые данные, касающиеся построения графиков, дифференцирования и интеграции.
Просмотрите полный список определенных функций на этой вики
Определение
Эта функция, обозначаемая 
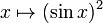
Для краткости мы пишем 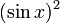
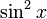
Ключевые данные
Значение
Четная функция
| пункт | |
|---|---|
| Домен по умолчанию | все действительные числа, то есть все 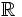 |
| диапазон | ![[0,1]](https://xn----8sbanwvcjzh9e.xn--p1ai/800/600/https/calculus.subwiki.org/w/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) , т.е. , т.е. 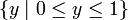 абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | 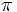 , то есть , то есть 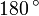 |
| локальное максимальное значение и очки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых числах, кратных 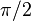 . . |
| местное минимальное значение и очки достижения | Все локальные минимальные значения равны 0 и достигаются при целых числах, кратных 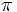 . . |
| точек перегиба (обе координаты) | нечетных кратных 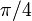 , со значением 1/2 в каждой точке. , со значением 1/2 в каждой точке. |
| производных | 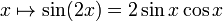 , то есть функция синусоидального угла. , то есть функция синусоидального угла. |
| вторая производная | 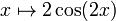 |
 производная производная |
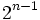 раз выражение, которое составляет раз выражение, которое составляет 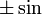 или или 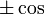 из из 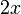 , в зависимости от остатка , в зависимости от остатка 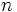 мод мод 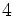 |
| антипроизводных |  |
| среднее значение за период | 1/2 |
| выражение в виде синусоидальной функции плюс постоянная функция | 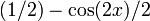 |
| важных симметрий | (следует из составной части четной функции с нечетной функцией четного, квадратная функция четная, а синус-функция нечетная) в более общем случае зеркально симметрично относительно любой вертикальной линии формы 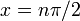 , , 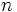 целое число. целое число.Кроме того, половина поворота симметрии вокруг всех точек формы 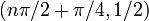 . . |
| описание интервала на основе увеличения / уменьшения и вогнутого вверх / вниз | Для каждого целого числа 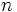 интервал от интервал от 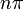 до до 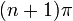 подразделяется на четыре части: подразделяется на четыре части: 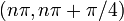 : увеличивается и вогнут до : увеличивается и вогнут до  : увеличивается и вогнут : увеличивается и вогнут 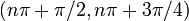 : уменьшается и вогнут, : уменьшается и вогнут, 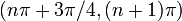 : уменьшается и вогнут до : уменьшается и вогнут до |
| и серия Тейлор | Степенной ряд около 0 (что, следовательно, также ряд Тейлора) равен 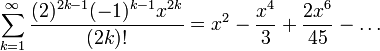 Это глобально сходящийся степенной ряд. |
Серия
Персоны
У нас есть следующие важные личности, связанные с 
График
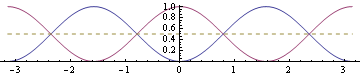
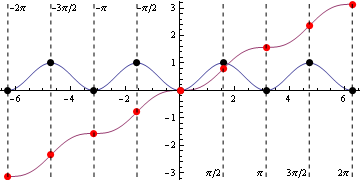
Вот график на интервале ![[-2pi,2pi]](https://xn----8sbanwvcjzh9e.xn--p1ai/800/600/https/calculus.subwiki.org/w/images/math/f/c/d/fcd3f9b324e7bfa715240a4c3fb40b9a.png)

Вот крупным планом график между 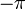
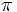
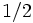
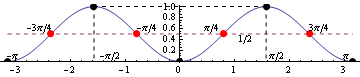
Красные пунктирные точки указывают точки перегиба, а черные пунктирные точки указывают локальные экстремальные значения.
Вот изображение, показывающее функцию (синяя) и функцию квадрата косинуса (фиолетовая) с пунктирной линией 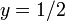
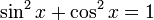
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило для дифференцирования, правило дифференцирования для степенных функций, функция синуса # Первая производная, формула двойного угла косинуса
У нас есть:
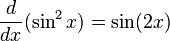
Мы можем сделать это двумя способами.
Используя цепное правило для дифференциации, мы имеем:
![! frac{d}{dx}[(sin x)^2] = 2sin x frac{d}{dx} (sin x) = 2sin x cos x](https://xn----8sbanwvcjzh9e.xn--p1ai/800/600/https/calculus.subwiki.org/w/images/math/2/b/2/2b2cc43fe01f388596699dd016369c93.png)
По формуле синусоидального угла это то же самое, что и 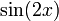
В качестве альтернативы, используя формулу косинуса двойного угла, мы переписываем:
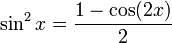
В отличии мы получаем:
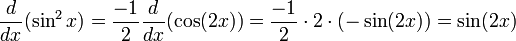
Вторая производная
Снова дифференцируя производную, получаем:
![frac{d^2}{dx^2}(sin^2x) = frac{d}{dx}[sin(2x)] = frac{d}{d(2x)}[sin(2x)]frac{d(2x)}{dx} = 2cos(2x)](https://xn----8sbanwvcjzh9e.xn--p1ai/800/600/https/calculus.subwiki.org/w/images/math/d/e/e/deec58ad406891f9ceb48cb74697b6ca.png)
График функции с производной
Заполните это позже
точек и интервалов интереса
Критические очки
Рассмотрим 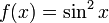
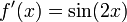
Это равно нулю точно в точках 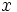
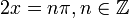
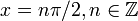
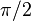
Интервалы увеличения и уменьшения
Функция 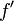
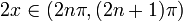

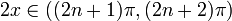

Местные экстремальные значения
Из информации о интервалах увеличения и уменьшения мы заключаем, что:
Интервалы вогнутой вверх и вогнутой вниз
Вторая производная 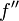
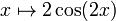

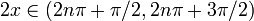

точек перегиба
Из определения интервалов, когда 
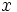
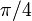
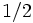
Интеграция
Первый антидериватив
ЧТО МЫ ИСПОЛЬЗУЕМ : формула двойного угла косинуса, рекурсивный вариант интегрирования по частям, интегрирование линейного преобразования функции
Использование формулы косинуса двойного угла
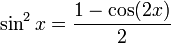
Теперь мы можем сделать интеграцию:

Чтобы интегрировать 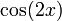
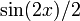
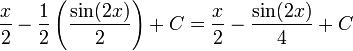
Использование интеграции по частям
Мы переписываем 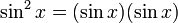
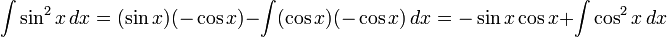
Теперь мы переписываем 
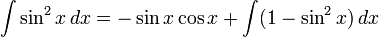
Если установить 

Переставляя, получаем:
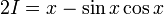
Это дает:
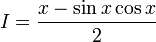
Итак, общее антидеривативное выражение:
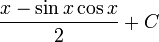
Используя формулу двойного угла синуса 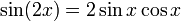
Для заданной непрерывной функции на связном множестве антипроизводные, полученные разными методами, должны отличаться на константу . В некоторых случаях антипроизводные могут быть в точности равны, но это , вообще не обязательно .
См нулевой производной подразумевает локально постоянную
График функции с антидеривативным
На рисунке ниже мы изображаем 
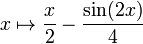
Черные точки соответствуют локальным крайним значениям для 
Определенные интегралы
Часть 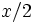

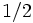

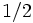
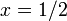
Таким образом, имеем:
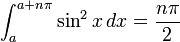
, где 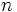
Среднее значение для 
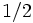

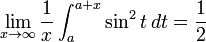
Преобразованные версии
На основе интегрирования 

Таким образом, мы видим, что среднее значение этой функции также составляет 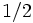

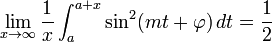
Высшее антипроизводное
Антидифференцировать 

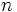
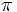
Силовая серия и серия Тейлор
Вычисление степенных рядов
Мы можем использовать личность:
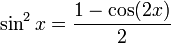
вместе с степенным рядом для функции косинуса, чтобы найти степенной ряд для 
Степенной ряд для функции косинуса сходится к функции везде и имеет вид:

Силовая серия для 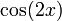
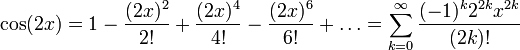
Силовая серия для 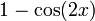

Разделив на 2, мы получим степенной ряд за 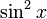

Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
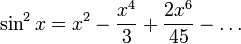
полиномов Тейлора как приближения
Обратите внимание, что, поскольку 

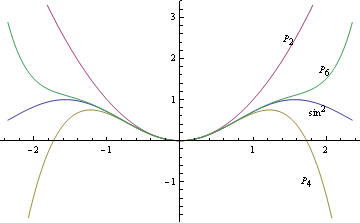
Предельные вычисления
Ноль порядка
Из степенных рядов получаем следующий предел:
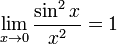
Таким образом, порядок нуля 
Этот предел может быть рассчитан многими способами:
Пределы высшего порядка
У нас есть предел:
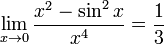
Этот предел может быть рассчитан многими способами:
,
диагоналей, отношений и свойств квадрата
-
- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12
9000al Aggar
- Классы
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 11
- Решения RS Aggarwal класса 10
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
Agaris Agard Agard Agard Agard Agard 2000 12000000
90 003 Решения RS Aggarwal класса 9
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE
9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия
Решения для класса 11 Биология
9 0003 NCERT Solutions Class 11 Бухгалтерия
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки 9 класса Глава 1
- Решения NCERT для науки 9 класса Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для 9 класса Наука Глава 4
- Решения NCERT для 9 класса Наука Глава 5
- Решения NCERT для 9 класса Наука Глава 6
- Решения NCERT для 9 класса Наука Глава 7
- Решения NCERT для 9 класса Научная глава 8
- Решения NCERT для 9 класса Научная глава
- Научные решения NCERT для 9 класса Научная глава 10
- Научные решения NCERT для 9 класса Научная глава 12
- Научные решения NCERT для 9 класса Научная глава 11
- Решения NCERT для 9 класса Научная глава 13
- Решения NCERT для 9 класса Научная глава 14
- Решения NCERT для класса 9 Science Глава 15
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10, глава 12
- Решения NCERT для математики класса 10, глава 13
- соль NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1
Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Класс 11 бизнес-дисциплин Syllabus
- Класс 11 Экономика Syllabus
- Класс 12 Бухгалтерский учебный план
- класс 12 бизнес-исследований S
18 ,
математика — самая быстрая реализация синуса, косинуса и квадратного корня в C ++ (не нужно быть очень точным)
Переполнение стека
- Товары
- Клиенты
- Случаи использования
- Переполнение стека
Публичные вопросы и ответы - Команды
Частные вопросы и ответы для вашей команды - предприятие
Частные вопросы и ответы для вашего предприятия - работы
Программирование и связанные с ним технические возможности карьерного роста - Талант
Нанимать технический талант - реклама
Связаться с разработчиками по всему миру
.
Для их вычисления следует запомнить основное тригонометрическое тождество: sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице). или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
Как вычислить тангенс в квадрате?
tg2(x)=tg(x)*tg(x)
Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку. На этой странице представлен самый простой онлайн калькулятор вычисления квадрата тангенса (тангенса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат тангенса любого угла.
Как в Excel sin в квадрате?
Осталось возвести получившуюся функцию в квадрат, в этом случае можно использовать либо символ «^», либо функцию «Степень». Напишем в ячейке «А1» формулу =SIN(РАДИАНЫ(90))^2, а в ячейке «А2»: =СТЕПЕНЬ(SIN(РАДИАНЫ(90));2).
Как найти косинус тангенс и котангенс если известен синус?
Тригонометрические формулы
- При известном синусе или косинусе числа можно найти его тангенс или котангенс: tg a = sin a/cos a.
- Можно найти синус числа, если известен его косинус и наоборот: sin2 a + cos2 a = 1.
- Найти тангенс можно через синус при известном косинусе: 1 + tg2 a = 1/cos2 a.
Чему равен синус в квадрате 30 градусов?
| значение угла α (градусов) | значение угла α в радианах (через число пи) | sin (синус) |
|---|---|---|
| 15 | π/12 | |
| 30 | π/6 | 1/2 |
| 45 | π/4 | √2/2 |
| 60 | π/3 | √3/2 |
Как найти косинус в квадрате?
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
Что такое тангенс?
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Это определение удобно использовать при изучении геометрических фигур. … Тангенс – это отношение синуса к косинусу.
Как написать синус в Excel?
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
…
Пример
| Формула | Описание | Результат |
|---|---|---|
| =SIN(ПИ()/2) | Синус пи/2 радиан. | 1,0 |
| =SIN(30*ПИ()/180) | Синус угла 30 градусов. | 0,5 |
| =SIN(РАДИАНЫ(30)) | Синус 30 градусов. | 0,5 |
Как найти котангенс если известен синус?
Тангенс это отношение синуса к косинусу: Tg(a)=Sin(a)/Cos(a). Котангенс это отношение косинуса к синусу: Ctg(a)=Cos(a)/Sin(a).
Как найти синус?
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Как перевести косинус на синус?
Перевод синуса в косинус и обратно выполняется посредством решения основного тригонометрического тождества sin2(x) + cos2(x) = 1. Смотрите также: — калькулятор вычисления синуса угла; — калькулятор вычисления косинуса угла.
Чему равен косинус от 0?
На тригонометрическом круге значения косинуса лежат на оси абсцисс (оси Ох). 0 градусов соответственно совпадает с числом 0. При проецировании этой точки на ось абсцисс получаем 1. Таким образом, косинус от 0 равен 1.
Чему равен косинус 30 градусов по таблице Брадиса?
Таблица Брадиса sin, cos
| sin | 0′ | 30′ |
|---|---|---|
| 60′ | 30′ | |
| 1° | 0175 | 0262 |
| 2° | 0349 | 0436 |
| 3° | 0523 | 0610 |
Чему равен синус 90 градусов?
sin (90°) = sin (π/2) = 1.
Как написать косинус в Excel?
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
…
Пример
| Формула | Описание | Результат |
|---|---|---|
| =COS(1,047) | Косинус 1,047 радиан | 0,5001711 |
| =COS(60*ПИ()/180) | Косинус 60 градусов | 0,5 |
| =COS(РАДИАНЫ(60)) | Косинус 60 градусов | 0,5 |
Как в Excel sin в квадрате?
Осталось возвести получившуюся функцию в квадрат, в этом случае можно использовать либо символ «^», либо функцию «Степень». Напишем в ячейке «А1» формулу =SIN(РАДИАНЫ(90))^2, а в ячейке «А2»: =СТЕПЕНЬ(SIN(РАДИАНЫ(90));2).
Как в Excel поставить степень над числом?
находишь закладку «вставка» выбираешь справа символ Ω, потом выделяешь число над которым необходимо вставить знак 5² (у меня 5) и выбираешь символ ², далее вставить и всё… Shurovik : Выделяете показатель степени и нажимаете комбинацию Ctrl+1.
Как пишется косинус в квадрате?
Косинус в квадрате, синус в квадрате
Для их вычисления следует запомнить основное тригонометрическое тождество: sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Как заставить Эксель посчитать в градусах?
Необходимо установить курсор в ячейку, которой будет присвоен результат; Выбрать в мастере функций «ГРАДУСЫ( )» или «РАДИАНЫ( )»; В появившемся окне указать значение или ячейку со значением, которое будет переводиться; Нажать кнопку «OK» или «Enter» на клавиатуре.
Как посчитать синус угла в Эксель?
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
…
Пример
| Формула | Описание | Результат |
|---|---|---|
| =SIN(ПИ()/2) | Синус пи/2 радиан. | 1,0 |
| =SIN(30*ПИ()/180) | Синус угла 30 градусов. | 0,5 |
| =SIN(РАДИАНЫ(30)) | Синус 30 градусов. | 0,5 |
Как вычислить синус в квадрате?
sin2(x)=sin(x)*sin(x)
Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку. На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Как в Excel сделать верхний индекс?
На вкладке Главная в группе Шрифт нажмите кнопку вызова диалогового окна «параметры шрифта». Нажмите сочетание клавиш CTRL+1. В разделе эффектыустановите флажок надстрочный или подстрочный текст и нажмите кнопку ОК.
Как поставить цифру сверху в Экселе?
Нажмите на клавиатуре горячие клавиши Ctrl+1. Появится окно «Формат ячеек». В нем вам необходимо в области «Видоизменение» установить отметку напротив пункта «Надстрочный». Нажмите ОК.
Как правильно возвести в квадрат?
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
Чему равен косинус в квадрате минус синус в квадрате?
Решение и ответ. косинус в квадрате плюс синус в квадрате равно единица. равен корню квадратному из выражения(единица минус синус квадрат).
Как посчитать cos 3?
cos3(x)=(cos(x))3
На этой странице представлен самый простой онлайн калькулятор вычисления косинуса в третьей степени (косинуса в 3 степени).
Как найти cos 3?
Для определения приближенного значения косинуса 3 радиан опустим на ось Ох перпендикуляр из точки 3 радиана. Координата х точки, в которой пересечется этот перпендикуляр с осью Ох, будет значением косинуса от 3 радиан.
Осталось возвести получившуюся функцию в квадрат, в этом случае можно использовать либо символ «^», либо функцию «Степень». Напишем в ячейке «А1» формулу =SIN(РАДИАНЫ(90))^2, а в ячейке «А2»: =СТЕПЕНЬ(SIN(РАДИАНЫ(90));2). Результат окажется одинаковым, только нужно выбрать себе удобный.
Как в Excel посчитать синус в градусах?
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
…
Пример
| Формула | Описание | Результат |
|---|---|---|
| =SIN(ПИ()/2) | Синус пи/2 радиан. | 1,0 |
| =SIN(30*ПИ()/180) | Синус угла 30 градусов. | 0,5 |
| =SIN(РАДИАНЫ(30)) | Синус 30 градусов. | 0,5 |
Как сделать косинус в квадрате в Excel?
Осталось возвести косинус в квадрат, сделать это можно двумя вариантами: оператором «^» или функцией «Степень». Тогда пропишем следующие формулы в ячейке «А1»: =СТЕПЕНЬ(COS(РАДИАНЫ(45));2), а в «А2»: =COS(РАДИАНЫ(45))^2.
Как синус возвести в квадрат?
sin 2 (x)=sin(x)*sin(x)
Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку. На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Как поставить косинус в Экселе?
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
Как в Excel посчитать косинус угла в градусах?
Это можно сделать двумя способами. Первый: умножить 136 на число пи и разделить произведение на 180. Второй: воспользоваться специальной функцией, которая переводит градусы в радианы.
Как в Excel посчитать в градусах?
Как в Excel поставить градусы с помощью сочетания клавиш
- Поместить курсор мышки в ячейку, в которой необходимо установить символ.
- Переключить клавиатуру на английскую раскладку сочетанием кнопок «Alt+Shift». …
- Зажать кнопку «Alt», а затем на вспомогательной клавиатуре справа набрать поочередно цифры 0176;
Как пишется косинус в квадрате?
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
Как найти корень в Excel?
В Microsoft Excel символ крышки (^) действует как оператор экспоненты или возведения в степень. Например, чтобы возвести число 5 во 2 степень, введите =5^2 в ячейку, что эквивалентно 52. Чтобы найти квадратный корень из числа в ячейке A2, введите: =A2^(1/2) или =A2^0,5.
Как построить график в Excel?
Создание графика в Office 2010
- Скопируйте данные листа-примера в пустой лист или откройте лист, содержащий данные, которые нужно отобразить на графике. …
- Выделите данные, которые вы хотите отобразить на графике.
- На вкладке Вставка в группе Диаграммы щелкните График.
- Выберите тип График с маркерами.
Как найти синус через косинус?
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Чему равен косинус икс в квадрате?
cos2х = 1 — 2sin²х.
Как написать число в квадрате в Excel?
Возведение в квадрат числа в отдельной ячейке
- Щелкните внутри ячейки на листе.
- Введите в ячейку =N^2, где N — это число, которое нужно возвести в квадрат. Например, чтобы вставить в ячейку A1 квадрат числа 5, введите в нее =5^2.
- Нажмите клавишу ВВОД, чтобы получить результат.
Как найти косинус угла в Эксель?
В Excel косинус угла можно найти с помощью функции COS, если этот угол измеряется в радианах. Функция COS экономит вам много времени и, возможно, много царапает голову, поскольку вам больше не нужно помнить, какая сторона треугольника примыкает к противоположному углу, а какая – к гипотенузе.
Как записать TG в Excel?
Простые тригонометрические функции в программе «Excel» выглядят следующим образом: Косинус (cos) – COS() Синус (sin) – SIN() Тангенс (tg) – TAN()
Как вычислить арктангенс в Excel?
Способ 1: ручной ввод функции
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа: =ATAN(число) Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. …
- Для вывода результатов расчета на экран нажимаем на кнопку Enter.
4 мар. 2017 г.
Площадь ромба можно вычислить разными способами.
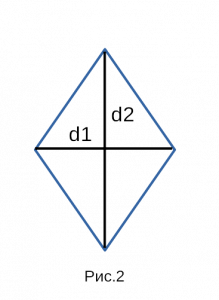
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Площадь ромба равна произведению
высоты на основание.
Формула площади ромба через параллелограмм:
( S = ah )
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Диагонали ромба являются биссектрисами его углов, кроме этого,
пересекаются под углом 90 градусов.
Формулировка площади ромба через две диагонали:
Площадь ромба равна половине произведения
одной диагонали на другую.
Формула площади ромба через две диагонали:
( S = frac{1}2d_1 d_2 )
d1 и d2 — диагонали;
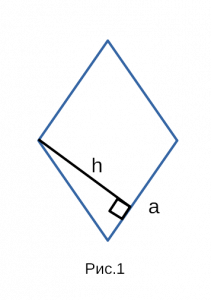
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
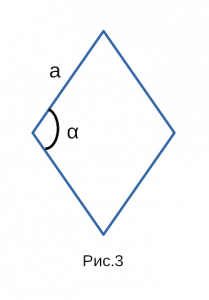
Формулировка площади ромба через синус и сторону в квадрате:
Площадь ромба равна произведению квадрата стороны
на синус угла прилежащего к этой стороне.
Формула площади ромба через синус и сторону в квадрате:
( S = a^2sinalpha )
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.