Как найти синусы углов равнобедренного треугольника

Как найти синус угла в равнобедренном треугольнике

Равнобедренным треугольником называется выпуклая геометрическая фигура из трех вершин и трех соединяющих их отрезков, два из которых имеют одинаковую длину. А синус — это тригонометрическая функция, которую можно использовать для численного выражения зависимости между соотношением длин сторон и величинами углов во всех треугольниках, включая и равнобедренные.

Инструкция

Если из исходных данных известна величина хотя бы одного угла (α) в равнобедренном треугольнике, это позволит найти и два других (β и γ), а значит и синус любого из них. Исходите из теоремы о сумме углов, которая утверждает, что в треугольнике она обязательно должна быть равна 180°. Если угол известной величины лежит между боковыми сторонами, величина каждого из двух других равна половине разности между 180° и известным углом. Значит, вы можете использовать в расчетах такое тождество: sin(β) = sin(γ) = sin((180°-α)/2). Если же известный угол примыкает к основанию треугольника, это тождество распадется на два равенства: sin(β) = sin(α) и sin(γ) = sin(180°-2*α).

Зная радиус (R) окружности, описанной около такого треугольника, и длину любой из сторон (например, а) можно не прибегая к вычислению тригонометрических функций рассчитать синус угла (α), лежащего напротив этой стороны. Используйте для этого теорему синусов — из нее вытекает, что нужная вам величина равна половине соотношения между длиной стороны и радиусом: sin(α) = ½*R/a.

Известные площадь (S) и длина боковой стороны (а) равнобедренного треугольника позволят рассчитать синус угла (β), лежащего напротив основания фигуры. Для этого удвойте площадь и поделите результат на возведенную в квадрат длину боковой стороны: sin(β) = 2*S/a². Если кроме длины боковой стороны известна и длина основания (b), квадрат можно заменить произведением длин этих двух сторон: sin(β) = 2*S/(a*b).

Если известны длины боковой стороны (а) и основания (b) равнобедренного треугольника, для вычисления синуса угла при основании (α) можно задействовать даже теорему косинусов. Из нее вытекает, что косинус этого угла равен половине отношения длины основания к длине боковой стороны: cos(α) = ½*b/a. Синус и косинус связаны таким равенством: sin²(α) = 1-cos²(α). Поэтому для вычисления синуса извлеките квадратный корень из разницы между единицей и четвертью соотношения квадратов длин основания и боковой стороны: sin(α) = √(1-cos2(α)) = √(1-¼*b²/а²).

Источники:

• рассчитать синус

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Равнобедренные треугольники

Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

6. В равнобедренном треугольнике:

— биссектрисы, проведенные из вершин при основании, равны;

— высоты, проведенные из вершин при основании, равны;

— медианы, проведенные из вершин при основании, равны.

7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.

8. Вписанная окружность точкой касания делит основание пополам.

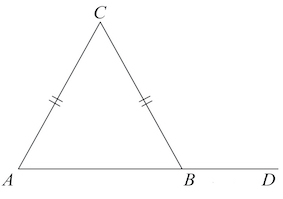
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

$∠BCD$ — внешний угол треугольника $АВС$.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$.

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

1. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
2. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
3. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= — cos BOC;$

$ctg BOA= — ctg BOC.$

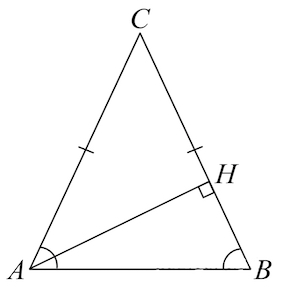
В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.

Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)

Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$

Рассмотрим прямоугольный треугольник $АНС$.

Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:

Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:

Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

В треугольнике $АВС$ $ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Далее подставим числовые данные и найдем $R$

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

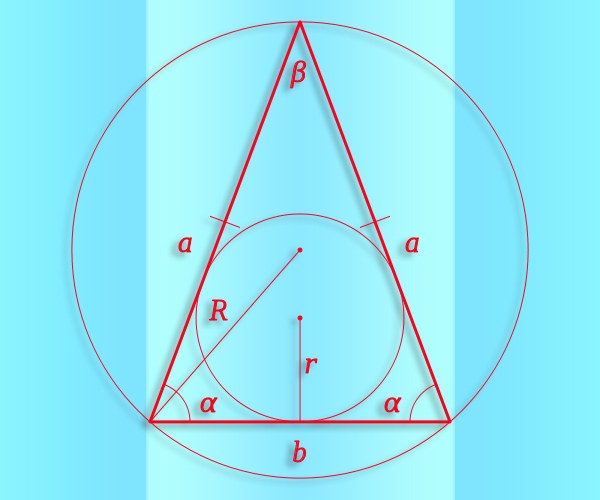
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° — 60°) = sin60° = 3/√2;
• sin150° = sin(180° — 30°) = sin30° = 1/2;
• sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Ты нашел то, что искал? Поделись с друзьями!

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол равен , . Найдите .

Задача решается за четыре секунды.

2 . В треугольнике угол равен , , . Найдите .

Найдем по теореме Пифагора.

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

21
Июл 2013

Категория: 01 Геометрия

01. Равнобедренный треугольник. Вычисление углов и длин

2013-07-21
2022-12-02

Автор: egeMax |

комментариев 12

Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.

Свойства:

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

6. В равнобедренном треугольнике:

— биссектрисы, проведенные из вершин при основании, равны;

— высоты, проведенные из вершин при основании, равны;

— медианы, проведенные из вершин при основании, равны.

7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.

8. Вписанная окружность точкой касания делит основание пополам.

$∠BCD$ — внешний угол треугольника $АВС$.

$∠BCD=∠A+∠B$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$.

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

1. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
2. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
3. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$sin BOA=sin BOC;$

$cos BOA= — cos BOC;$

$tg BOA= — tg BOC;$

$ctg BOA= — ctg BOC.$

Теорема Менелая:

Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то

${АС_1}/{С_1 В}·{ВА_1}/{А_1 С}·{СВ_1}/{В_1 А}=1$

Теорема синусов.

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

${a}/{sin⁡α}={b}/{sin⁡β}={c}/{sin⁡γ}=2R$, где $R$ — радиус описанной около треугольника окружности.

Теорема косинусов.

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$a^2=b^2+c^2-2·b·c·cosα.$

• Прямоугольный треугольник заключает в себе великое множество различных отношений между всеми своими составляющими. Один из углов в таком треугольнике имеет величину 90°, за счет чего и появляются его особенные свойства. Стороны, прилегающие к прямому углу, называются катетами прямоугольного треугольника, а сторона, лежащая напротив него – гипотенузой. Прямой угол в основе треугольника регулирует отношение сторон таким образом, что зная их можно рассчитать любой острый угол. Отношение противолежащего углу α катета a к гипотенузе c называется синусом угла α и записывается следующим образом:
  

  Разделив катет на гипотенузу, мы получим значение синуса, соответствующее определенной градусной мере, найти которую можно в таблице синусов. Таблица основных значений синусов приведена ниже, а полную версию можно найти по ссылке.

  

  Свойства

  Синус угла sin(α) — есть отношение противолежащего катета a к гипотенузе c.

  

  Таблица синусов

  Синус угла 0° градусов	0	0.000
  Синус угла 30° градусов	1/2	0.500
  Синус угла 45° градусов	√2/2	0.707
  Синус угла 60° градусов	√3/2	0.866
  Синус угла 90° градусов	1	1