Как найти систематическое отклонение

Несмещенной
состоятельной, эффективной оценкой для
генерального среднего ā нормального
распределения является выборочное
среднее х,

определяемое
по формуле:

Где х₁;
х₂;…;х_n
– совокупность значений случайных
величин х.

Несмещенную оценку
для среднего квадратического отклонения
определяют по формуле:

где

если a
неизвестно, то по формуле (1):

(1)

если а
известно,
то по формуле (2):

(2)

Значение коэффициента
Мк дается в таблице, где к = n-1, если а
неизвестно, и к = n, если а известно.

При значениях
объема выборок n
> 60 оценку для среднего квадратического
отклонения σ находят по формуле (1), а
если а неизвестно, или по формуле (2),
если а известно.

Несмещенными
оценками для дисперсии σ²
нормального распределения являются
выборочные характеристики:

при неизвестном
а

при известном а

1.14.Оценка среднего квадратического отклонения результата измерения

Среднее квадратическое
отклонение результата измерения
оценивают по формуле:

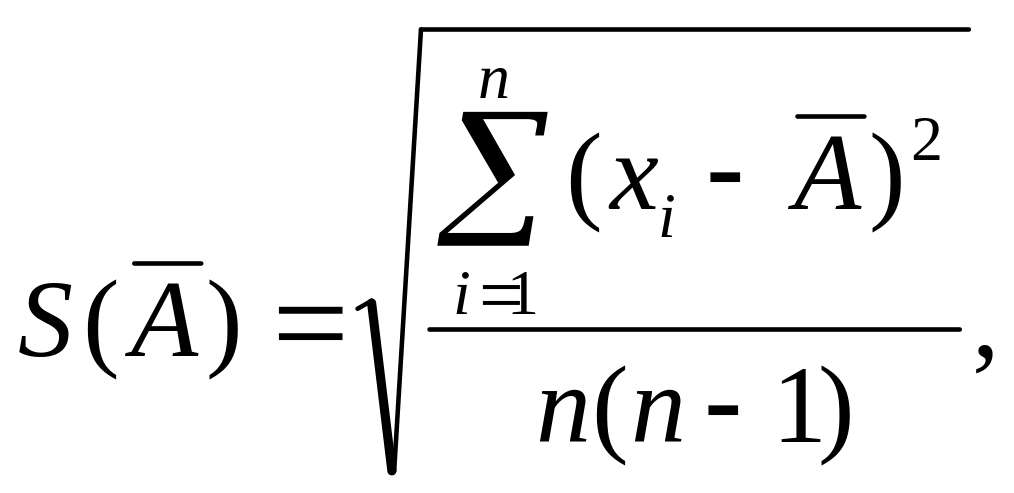
где S(Ã)
– оценка среднего квадратического
отклонения результата измерения;

à – результат
измерения (ср. арифметическое исправленных
результатов наблюдений); х_i
– i-й
результат наблюдений.

1.15. Вычисление доверительных границ случайной погрешности результата измерения

Доверительные
границы случайной погрешности результата
измерения устанавливают для результатов
наблюдений, принадлежащих нормальному
распределению. Если это условие не
выполняется, то методы вычисления
доверительного интервала случайной
погрешности должны быть указаны в
методике выполнения конкретных измерений.

Если заранее
известно, что результаты наблюдений
принадлежат нормальному распределению,
доверительные границы Є (без учета
знака) случайной погрешности результата
измерения находят по формуле:

Є=t_sS(
)

Где t_s
– коэффициент Стьюдента, который в
зависимости от доверительной вероятности
Р и числа результатов наблюдений n
находят по таблицам. При числе наблюдений
n
> 50 для проверки принадлежности их к
нормальному распределению используют
критерий х²
(Пирсона) или ω²
(Мизеса-Смирнова). Если 50 > n
> 15, то используют составной критерий.

1.16. Вычисление доверительных границ погрешности результата измерени3

1

Если отношение
неисключенных систематических
погрешностей к среднему квадратическому
отклонению результата измерения Q/S(Ã)
< 0,8, то неисключенными систематическими
погрешностями пренебрегают и принимают
что граница погрешности результата ∆
= Є. Если Q/S(Ã)
> 8, то пренебрегают случайной погрешностью
и принимают, что граница погрешности
результата Δ = Q.
Однако , следует помнить, что погрешность,
возникающая вследствие пренебрежения
одной из составляющих погрешности
результата измерений при выполнении
указанных неравенств, не должна превышать
15 %. Если неравенства не выполняются, то
границу погрешности результата измерения
находят путем построения композиции
распределений случайных и не исключенных
систематических погрешностей,
рассматриваемых как случайные величины.

В результате
определения доверительных границ
случайных погрешностей, вычисляют
границы погрешности результата измерения
Δ без учета знака по формуле:

Δ = К*S_Σ

Где
К – коэффициент, зависящий от соотношения
случайной и неслучайной систематической
погрешностей;

S_Σ
– оценка суммарного среднего
квадратического отклонения результата
измерения.

К

оэффициент
К вычисляют по эмпирической формуле:

Суммарное
среднее квадратического отклонение
результата измерения оценивают по
формуле: Є

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Под смещение (или даже систематическая ошибка ) к тому , что понимает отклонение от более измеренного значения в виде измеряемой величины их истинного значения , однонаправленные и обусловлена обнаруживаемой в принципе причин. Его нельзя распознать, когда измерения повторяются в тех же условиях . Отклонения, возникающие между отдельными измеренными значениями во время таких повторений, называются случайными отклонениями .

Поэтому систематические отклонения вызывают сдвиг в одну сторону; они обычно означают слишком высокие или всегда слишком низкие измеренные значения. Типичным примером этого являются отклонения, вызванные неправильно настроенными измерительными приборами . Систематическое отклонение измерительного устройства не обязательно должно быть постоянным во всем диапазоне измерения (например, в случае неправильно отрегулированного термометра , который показывает высокие температуры слишком высокие и низкие температуры слишком низкие).

Систематического отклонения можно избежать, только если известна причина. Причины измерения могут заключаться в неправильно настроенном измерительном устройстве, неправильных показаниях снова и снова, изменении исходной реальности, вызванном измерительным устройством, влиянии окружающей среды, использовании неподходящего метода оценки или измерения и многое другое.

За пределами измерительной техники, например, в связи с IEC 61508 (функциональная безопасность систем, связанных с безопасностью), систематические ошибки также рассматриваются как «встроенные» ошибки — повреждения, присутствующие в каждом продукте. В этом смысле, например, ошибка Pentium FDIV была одной из систематических ошибок, потому что правильная обработка неправильно реализованной функции приводила к точно таким же воспроизводимым ошибкам вычислений в каждой произведенной копии процессора Pentium. — В социальных исследованиях систематический отклонения известны как тенденция отклика .

О номенклатуре

Систематическое отклонение измерения может состоять из известного и неизвестного отклонения.

При получении в одинаковых условиях измеренных значений систематическая ошибка является постоянной ошибкой измерения, это смещение (нулевое) смещение , полка или подобное. Медленно увеличивающееся / уменьшающееся отклонение измерения (например, в случае изменения отображения, которое становится распознаваемым с течением времени) также носит систематический характер; это называется трендом (также известным как смещение ) или дрейфом . Тенденции и отклонения относительно легко обнаружить путем повторных измерений. Часто они возвращаются к незамеченным температурным воздействиям . Причина — даже старение .

В английском языке слово bias также используется для обозначения систематического сдвига , но в электронике это также можно понимать как неизбежную или преднамеренную одностороннюю предварительную нагрузку .

Причины систематических ошибок измерения

В причинах систематических ошибок измерения разнообразны. В частности, это:

• Несовершенство измерительных устройств ( отклонение измерительного устройства , например, неправильная настройка , несоблюдение калибровки ),
• Влияния , такие как отопление, износ, старение (например , свободные части на измерительном устройстве, тепловое расширение, направленное отклонение или из-of округлость из осей ),
• Отклонения фактических значений влияющих переменных от предполагаемых (влияющие эффекты, например, самонагрев, рефракция , асимметричные эффекты температуры или ветра, вибрация в геологической среде),
• Отклонения реально существующего объекта измерения от предполагаемого,
• Обратная связь, когда измеряемая величина регистрируется измерительным устройством (например, отклонение обратной связи из-за внутреннего потребления в электрических измерительных устройствах),
• отклонения , вызванные наблюдателем (например , односторонние прицеливания ошибки , параллакс ошибки );
• Использование отношения между величинами, приводящего к результату измерения, не соответствующего фактической связи между этими величинами

Фальсификации из-за ошибок или невнимательности со стороны наблюдателя (например, неправильное числовое значение при чтении ), непредвиденные события (например, удары) или возникновение грубых ошибок , которых всегда можно избежать, не могут быть классифицированы здесь. Однако при корректировке их обычно можно распознать, когда их остаток превышает в 2–3 раза стандартное отклонение.

пример

Даже простое измерение с помощью линейки дает возможность систематических отклонений измерения.

1. Инструментальный (неправильное масштабирование): если линейка или рулетка находится на солнце, она нагревается и расширяется. Если измерение проводится с ним, измерение всегда немного короче. Однако, зная температуру линейки и ее коэффициент теплового расширения , вы можете устранить это влияние расчетным путем. Систематическое отклонение теперь учитывается в модели измерения и, таким образом, становится безвредным — в рамках знания физических отношений и необходимых данных. Без этой модели работа с измерительным устройством помогает справиться с эталонными условиями, для которых он разработан. Если держатель шкалы изменяется из-за старения (особенно у пластика), новая регулировка в этом простом примере невозможна. В лучшем случае калибровку можно использовать для определения коэффициента, на который необходимо скорректировать соответствующее считываемое значение.
2. Неправильное обращение: с другой стороны, если вы поместите линейку под углом на заготовку во время измерения, показания теперь будут систематически искажаться. Но если вы знаете угол, под которым линейка была размещена неправильно (или смотрела на нее косо), вы можете учесть это, рассчитав угол.
3. Неблагоприятные обстоятельства: они могут включать неровную или скользящую поверхность, раздражающую тень от чешуи и т.п. Здесь математически можно не много исправить, но измерения следует повторять в разных условиях окружающей среды.

Внутренняя и внешняя точность

В термине « внешняя точность » обычно понимаются систематические отклонения, в то время как «внутренняя точность», также известная как точность , обычно соответствует разбросу, когда измерение просто повторяется. Оба значения обычно указываются в виде стандартного отклонения . Разница между ними может стать очевидной при смене измерительного прибора (см. 1.), наблюдателя  (2.) или внешних обстоятельств (3.), таких как погодная ситуация .

Астрономической широты определения со звездами и проход инструмента или цифровой астролябии имеет внутреннюю точность 0,1», но может варьироваться в зависимости от 0.5″ от одной ночи к следующему. Причина таких «вечерних ошибок» кроется в аномалиях в атмосферных слоях ( астрономическая рефракция , рефракция купола или холла ) или в небольших температурных эффектах , например, при изгибе телескопа .

Работа с систематической ошибкой измерения

Определение систематических отклонений измерения (цитата из)

1. Детективная работа, в которой вы должны выявить источники ошибок,
2. физико-философское рассмотрение, лежит ли незнание в теоретических рамках или за их пределами,
3. Профессиональный анализ данных, при котором ошибки оцениваются по степени важности и, при необходимости, вводятся подходящие корректоры.

Систематическое отклонение, которое остается постоянным во времени, не может быть определено или на него невозможно повлиять повторением; вы должны сделать известное отклонение

• уменьшить или устранить путем регулировки или
• предотвратить, соблюдая допустимые условия окружающей среды,
• Избегайте изменения настройки измерения (например, с двумя круговыми положениями на теодолите или путем компенсации ),
• принять во внимание через оценку (см. сокращение (измерение) ),
• Примите и учтите при указании допусков или пределов погрешности .

Неизвестное систематическое отклонение измерения может быть оценено только при наличии достаточного опыта и ограничено с помощью интервалов.

Примеры неизвестных систематических отклонений постоянной времени

• механическая настройка измерительного устройства на правильное значение , которое может быть достигнуто только с конечной точностью ,
• Отвод тепла через защитную трубку термометра в месте измерения температуры.

Для неизвестной и наблюдаемой в принципе, но не определенной в деталях погрешности измерения добавляется предел погрешности (или величина порога отклонения) такой, какая есть. Это беззнаковое по определению.

В случае дрейфующего измерительного устройства отклонения измерения подвержены тенденции — в отличие от случайных отклонений, которые разбегаются беспорядочно. Чтобы обнаружить это, в отличие от постоянных систематических отклонений, требуются повторные измерения в виде временных рядов .

С другой стороны, статистика разработала свои собственные совершенно другие методы обработки временных рядов , например, биржевых цен.

Смотри тоже

• Распространение ошибки
• Ошибка индекса , фид курса
• Искажение (электротехника) , искажение (эмпиризм)
• Эффект дизайна

Индивидуальные доказательства

1. ↑ Термин погрешность измерения не соответствует действующему стандарту DIN1319-1, но все же время от времени встречается.
2. ↑ ^{a b c d} DIN 1319-1, Основы измерительной техники — Часть 1: Основные термины . 1995 г.
3. ↑ ^{a b} Лотар Папула: Математика для инженеров и естествоиспытателей Том 2 . Vieweg + Teubner, 6-е издание, 2011 г., стр. 651.
4. ^ ^{A b} Георг Стрек: Введение в статистику для геоэкологов и других естествоиспытателей . Книги по запросу 2004, с. 159.
5. ↑ Мартин Эрдманн, Томас Хеббекер: Experimentalphysik 5: Современные методы анализа данных . Springer 2013, стр.139.

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

• среднеквадратическое отклонение,
• среднее квадратическое отклонение,
• среднеквадратичное отклонение,
• квадратичное отклонение,
• стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

• в финансах в качестве меры волатильности,
• в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

• А -> (19 + 21 + 19+ 21) / 4 = 20
• Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

• в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
• в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

• стандартное отклонение компании A = 1,
• стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

1. Вычесть среднее значение из каждого числа
2. Возвести каждый результат в квадрат (так получатся квадраты разностей)
3. Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

• одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
• двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
• трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

• при <10% выборка слабо вариабельна,
• при 10% – 20 % — средне вариабельна,
• при >20 % — выборка сильно вариабельна.

Узнайте также про:

• Корреляции,
• Метод Крамера,
• Метод наименьших квадратов,
• Теорию вероятностей
• Интегралы.

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом  (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

• Определите среднее (простое среднее арифметическое ряда значений).
• Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
• Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее   мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

   

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки =  мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

.

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

.

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

.

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

.

Для второго примера получится:

.

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Была ли эта статья полезной?