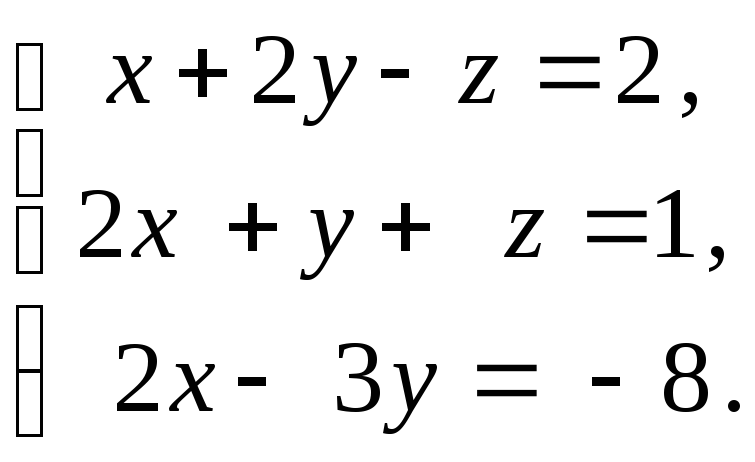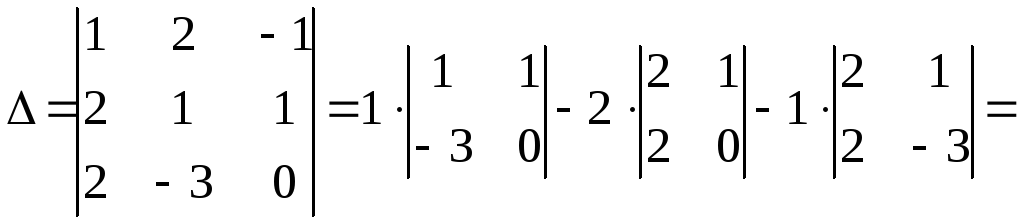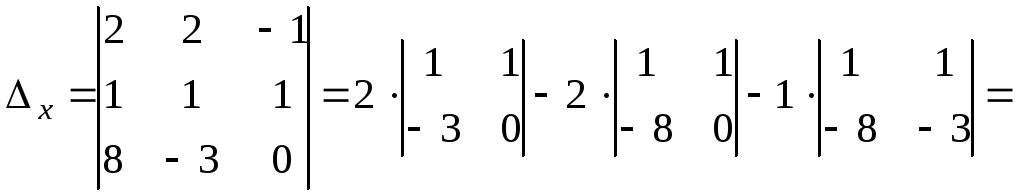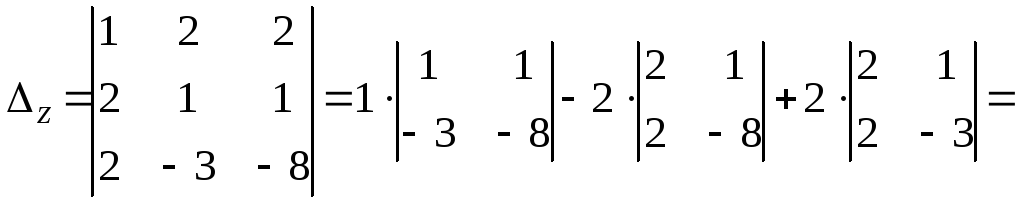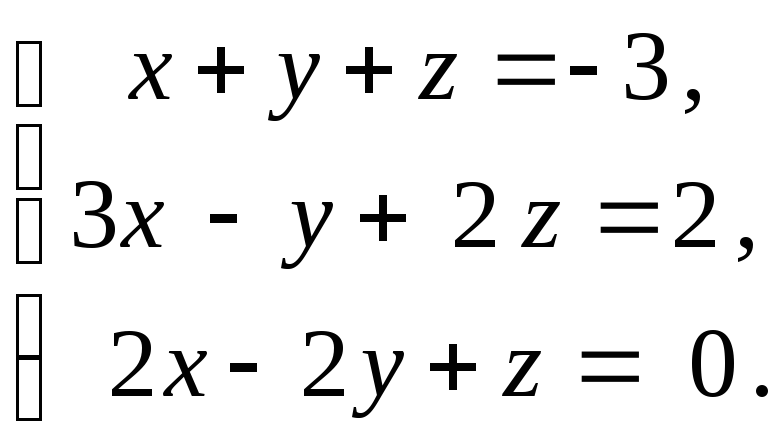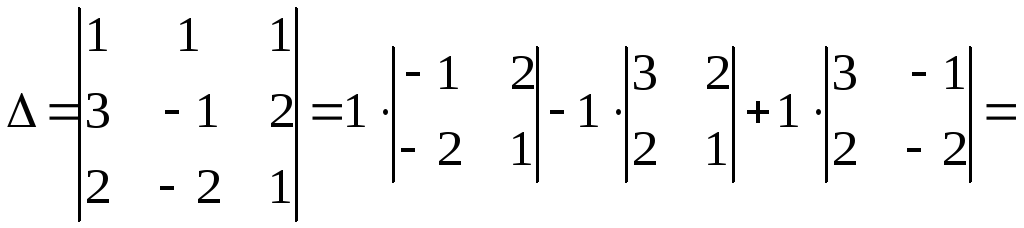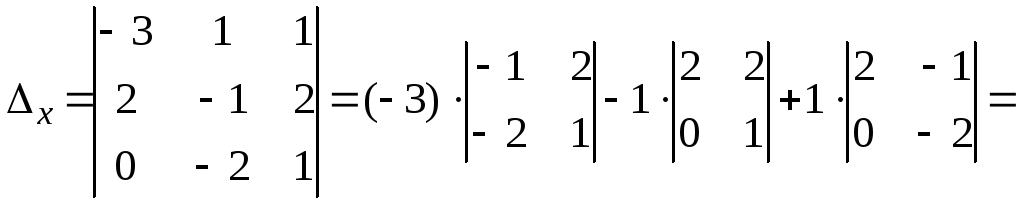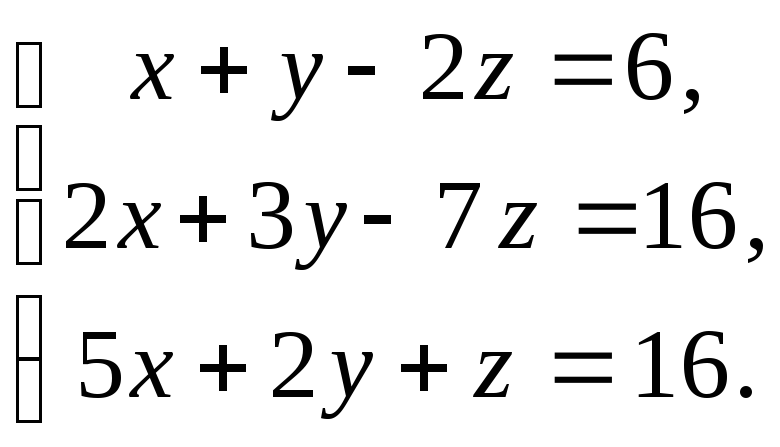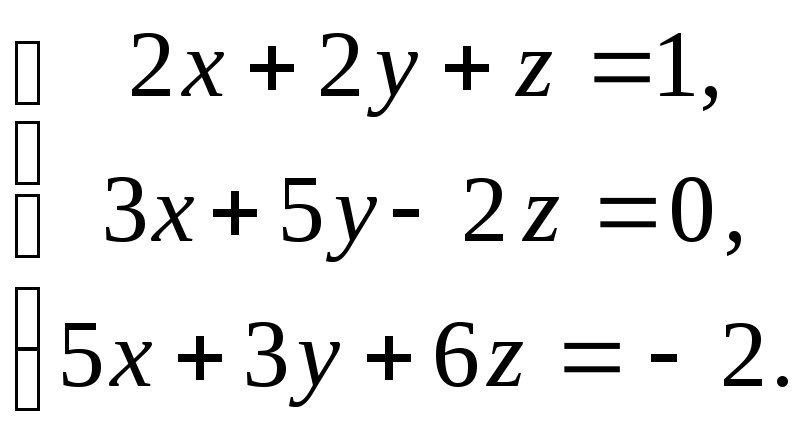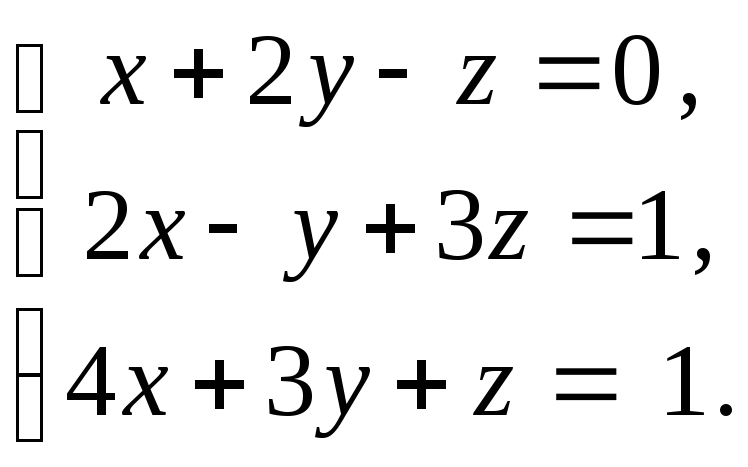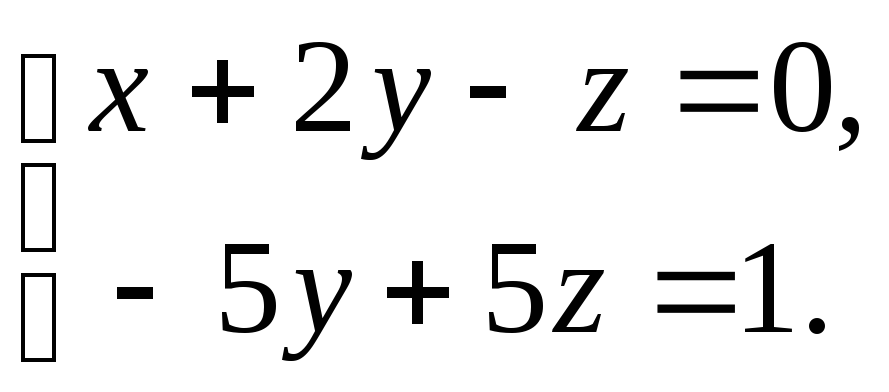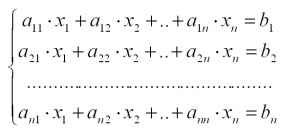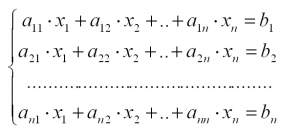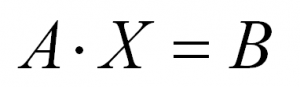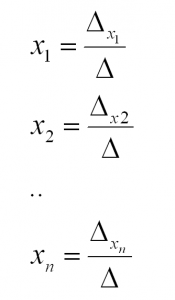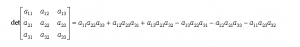Как найти систему линейных уравнений методом крамера

(схема 16)

Дадим ряд необходимых определений.

Система линейных уравнений называется неоднородной,
если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее
свободные члены равны нулю.

Решением системы уравнений называется упорядоченный набор чисел, который, будучи
подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.

Система уравнений называется совместной, если она
имеет хотя бы одно решение, и несовместной, если она решений не
имеет.

Совместная система уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет более
одного решения.

Рассмотрим неоднородную систему линейных
алгебраических уравнений, имеющую при n=m следующий
общий вид:

.                                                                                                                                                  (1.5) 

Главной матрицей A системы
линейных алгебраических уравнений называется матрица, составленная из
коэффициентов, стоящих при неизвестных:

.

Определитель главной матрицы системы называется главным
определителем и обозначается ∆.

Вспомогательный определитель ∆_i  получается
из главного определителя путем замены i-го
столбца на столбец свободных членов.

Теорема 1.1
(теорема Крамера). Если главный
определитель системы линейных алгебраических уравнений отличен от нуля, то
система имеет единственное решение, вычисляемое по формулам:

.                                                                                                                                                                        (1.6)

 Если
главный определитель ∆=0, то система либо 
имеет бесконечное множество решений (при всех нулевых вспомогательных
определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного
из вспомогательных определителей).

В свете приведенных выше определений, теорема Крамера может быть сформулирована иначе: если
главный определитель системы линейных алгебраических уравнений отличен от нуля,
то система является совместной определенной и при этом ; если главный определитель нулевой, то система является
либо совместной неопределенной (при всех ∆_i=0),
либо несовместной (при отличии хотя бы одного из ∆_i от нуля).

После этого следует провести проверку полученного
решения.

Пример 1.4.  Решить
систему методом Крамера 

Решение.  Так
как главный определитель системы

 отличен от нуля, то система имеет единственное
решение. Вычислим вспомогательные определители

Воспользуемся
формулами Крамера (1.6):
 

Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла
и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.

                                                                   
                                     Таблица 1.4                                 

Определить стоимость 1 единицы продукции молокоцеха
каждого вида.

Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z –
1 кг
творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из
трех дней реализации можно отобразить следующей системой:

.

Решим систему методом Крамера. Найдем главный
определитель системы по формуле (1.2):

         

     Так
как он отличен от нуля, то система имеет единственное решение. Вычислим
вспомогательные определители с помощью формулы (1.2):

        

По формулам Крамера (1.6) имеем:

Вернувшись к обозначениям, видим, что стоимость 1
литра молока равна 44 рубля, 1
кг масла – 540 рублей, 1 кг творога – 176 рублей

Примечание. Как видно, процесс вычисления определителей вручную с
помощью калькулятора трудоемок, поэтому на практике используют персональный
компьютер. Так, для решения систем линейных алгебраических уравнений методом
Крамера в MS Excel высчитывают ее главный и вспомогательные определители
с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек
и элементы матрицы, определитель которой находится.

В MathCAD для
нахождения определителя пользуются палитрой оператора Matrix

Вопросы для
самопроверки

Метод Крамера. Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:

1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $Deltaneq 0$.
2. Для каждой переменной $x_i$($i=overline{1,n}$) необходимо составить определитель $Delta_{x_i}$, полученный из определителя $Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
3. Найти значения неизвестных по формуле $x_i=frac{Delta_{x_{i}}}{Delta}$ ($i=overline{1,n}$).

Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.

Пример №1

Решить СЛАУ $left{begin{aligned}
& 3x_1+2x_2=-11;\
& -x_1+5x_2=15.
end{aligned}right.$ методом Крамера.

Решение

Матрица системы такова: $ A=left( begin{array} {cc} 3 & 2\ -1 & 5 end{array} right)$. Определитель этой матрицы:

$$Delta=left| begin{array} {cc} 3 & 2\ -1 & 5 end{array}right|=3cdot 5-2cdot(-1)=17.$$

Как вычисляется определитель второго порядка можете глянуть здесь.

Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $Delta_{x_1}$ и $Delta_{x_2}$. Определитель $Delta_{x_1}$ получаем из определителя $Delta=left| begin{array} {cc} 3 & 2\ -1 & 5 end{array}right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $left(begin{array} {c} -11\ 15end{array}right)$:

$$
Delta_{x_1}=left|begin{array}{cc}-11&2\15&5end{array}right|=-55-30=-85.
$$

Аналогично, заменяя второй столбец в $Delta=left|begin{array}{cc}3&2\-1&5end{array}right|$ столбцом свободных членов, получим:

$$
Delta_{x_2}=left|begin{array} {cc} 3 & -11\ -1 & 15end{array}right|=45-11=34.
$$

Теперь можно найти значения неизвестных $x_1$ и $x_2$.

$$x_1=frac{Delta_{x_1}}{Delta}=frac{-85}{17}=-5;;x_2=frac{Delta_{x_2}}{Delta}=frac{34}{17}=2.$$

В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:

$$left{begin{aligned}
& 3x_1+2x_2=3cdot(-5)+2cdot{2}=-11;\
& -x_1+5x_2=-(-5)+5cdot{2}=15.
end{aligned}right.$$

Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.

Ответ: $x_1=-5$, $x_2=2$.

Пример №2

Решить СЛАУ $
left{begin{aligned}
& 2x_1+x_2-x_3=3;\
& 3x_1+2x_2+2x_3=-7;\
& x_1+x_3=-2.
end{aligned} right.$, используя метод Крамера.

Решение

Определитель системы:

$$Delta=left| begin{array} {ccc} 2 & 1 & -1\ 3 & 2 & 2 \ 1 & 0 & 1 end{array}right|=4+2+2-3=5.$$

Как вычисляется определитель третьего порядка можете глянуть здесь.

Заменяя первый столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_1}$:

$$
Delta_{x_1}=left| begin{array} {ccc} 3 & 1 & -1\ -7 & 2 & 2 \ -2 & 0 & 1 end{array}right|=6-4-4+7=5.
$$

Заменяя второй столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_2}$:

$$
Delta_{x_2}=left| begin{array} {ccc} 2 & 3 & -1\ 3 & -7 & 2 \ 1 & -2 & 1 end{array}right|=-14+6+6-7-9+8=-10.
$$

Заменяя третий столбец в $Delta$ столбцом свободных членов, получим $Delta_{x_3}$:

$$
Delta_{x_3}=left| begin{array} {ccc} 2 & 1 & 3\ 3 & 2 & -7 \ 1 & 0 & -2 end{array}right|=-8-7-6+6=-15.
$$

Учитывая все вышеизложенное, имеем:

$$
x_1=frac{Delta_{x_1}}{Delta}=frac{5}{5}=1;; x_2=frac{Delta_{x_2}}{Delta}=frac{-10}{5}=-2; ; x_3=frac{Delta_{x_3}}{Delta}=frac{-15}{5}=-3.
$$

Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:

$$left{begin{aligned}
& 2x_1+x_2-x_3=2cdot{1}+(-2)-(-3)=3;\
& 3x_1+2x_2+2x_3=3cdot{1}+2cdot(-2)+2cdot(-3)=-7;\
& x_1+x_3=1+(-3)=-2.
end{aligned} right.$$

Проверка пройдена, решение системы уравнений методом Крамера найдено верно.

Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.

Пример №3

Решить СЛАУ $left{begin{aligned}
& 2x_1+3x_2-x_3=15;\
& -9x_1-2x_2+5x_3=-7.
end{aligned}right.$ используя метод Крамера.

Решение

Матрица системы $ left( begin{array} {ccc} 2 & 3 & -1\ -9 & -2 & 5 end{array} right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:

$$

left { begin{aligned}
& 2x_1+3x_2=x_3+15;\
& -9x_1-2x_2=-5x_3-7.

end{aligned} right.

$$

Теперь матрица системы $ left( begin{array} {cc} 2 & 3 \ -9 & -2 end{array} right) $ стала квадратной, и определитель её $Delta=left| begin{array} {cc} 2 & 3\ -9 & -2 end{array}right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:

$$
begin{aligned}
& Delta_{x_1}
=left| begin{array} {cc} x_3+15 & 3\ -5x_3-7 & -2 end{array}right|
=-2x_3-30-left(-15x_3-21right)
=13x_3-9;\
\
& Delta_{x_2}
=left| begin{array} {cc} 2 & x_3+15\ -9 & -5x_3-7 end{array}right|
=-10x_3-14-left(-9x_3-135right)
=-x_3+121.
end{aligned}
$$

$$
x_1=frac{Delta_{x_1}}{Delta}=frac{13x_3-9}{23};;
x_2=frac{Delta_{x_2}}{Delta}=frac{-x_3+121}{23}.
$$

Ответ можно записать в таком виде: $left{begin{aligned}
& x_1=frac{13x_3-9}{23};\
& x_2=frac{-x_3+121}{23};\
& x_3in R.
end{aligned}right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.

Примечание

В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$left{begin{aligned}
& 2x_1-5x_2+10x_3=14;\
& -4x_1+10x_2-7x_3=5.
end{aligned}right.$. Если перенести в правые части уравнений $x_3$, получим: $
left{begin{aligned}
&2x_1-5x_2=-10x_3+14;\
&-4x_1+10x_2=7x_3+5.
end{aligned}right.$. Определитель данной системы $Delta=left| begin{array} {cc} 2 & -5\ -4 & 10 end{array}right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
left{begin{aligned}
&2x_1+10x_3=5x_2+14;\
&-4x_1-7x_3=-10x_2+5.
end{aligned}right.$, определитель которой $Delta=left| begin{array} {cc} 2 & 10\ -4 & -7 end{array}right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.

Пример №4

Решить СЛАУ

$$left{begin{aligned}
&x_1-5x_2-x_3-2x_4+3x_5=0;\
&2x_1-6x_2+x_3-4x_4-2x_5=0; \
&-x_1+4x_2+5x_3-3x_4=0.
end{aligned}right.$$

методом Крамера.

Решение

Матрица системы $left(begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \
2 & -6 & 1 & -4 & -2 \
-1 & 4 & 5 & -3 & 0
end{array}right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:

$$
left{begin{aligned}
& x_1-5x_2-x_3=2x_4-3x_5;\
& 2x_1-6x_2+x_3=4x_4+2x_5; \
& -x_1+4x_2+5x_3=3x_4.
end{aligned}right.$$

$$
begin{aligned}
& Delta
=left| begin{array} {ccc} 1 & -5 & -1\ 2 & -6 & 1\-1 & 4 & 5 end{array}right|
=19;\
\
& Delta_{x_1}
=left| begin{array} {ccc} 2x_4-3x_5 & -5 & -1\ 4x_4+2x_5 & -6 & 1\3x_4 & 4 & 5 end{array}right|
=-17x_4+144x_5;\
\
& Delta_{x_2}
=left| begin{array} {ccc} 1 & 2x_4-3x_5 & -1\ 2 & 4x_4+2x_5 & 1\-1 & 3x_4 & 5 end{array}right|
=-15x_4+41x_5;\
\
& Delta_{x_3}
=left| begin{array} {ccc} 1 & -5 & 2x_4-3x_5\ 2 & -6 & 4x_4+2x_5\-1 & 4 & 3x_4 end{array}right|
=20x_4-4x_5.
end{aligned}
$$

Ответ таков: $left{begin{aligned}
& x_1=frac{-17x_4+144x_5}{19};\
& x_2=frac{-15x_4+41x_5}{19};\
& x_3=frac{20x_4-4x_5}{19}; \
& x_4in R; ; x_5in R.
end{aligned}right.$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.

Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.

Простое объяснение принципов решения линейных уравнений по методу Крамера и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Метод Крамера

Пусть
дана система трех линейных уравнений:

(1)

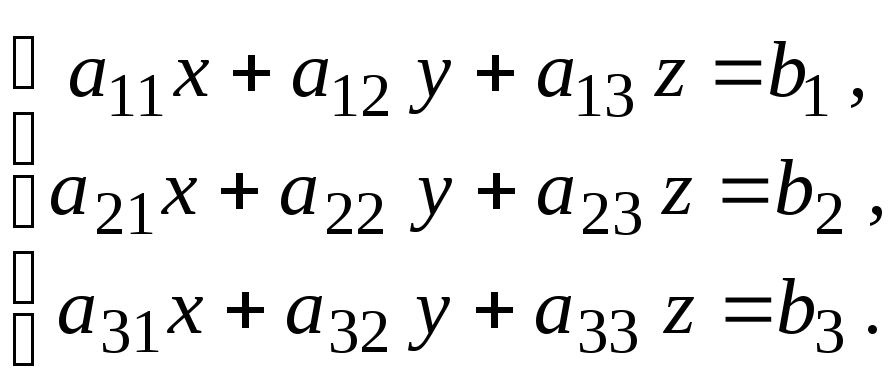
Для
решения системы линейных уравнений
методом Крамера из коэффициентов при
неизвестных составляется главный
определитель
системы .
Для системы (1) главный определитель
имеет вид
.

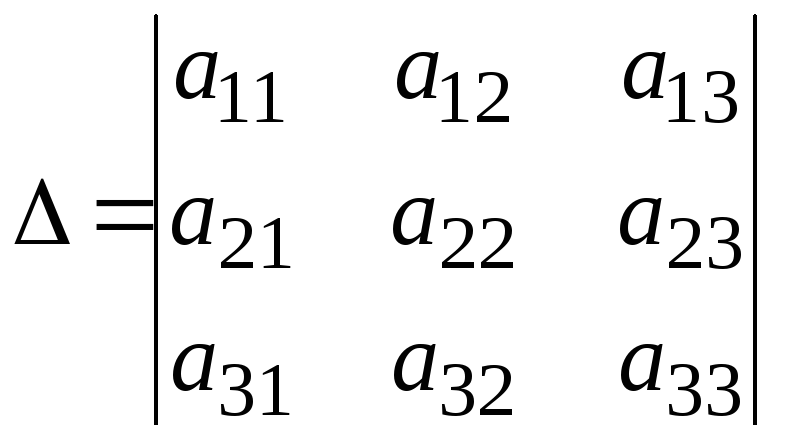
Далее
составляются определители по переменным
,,.
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть

,
,.

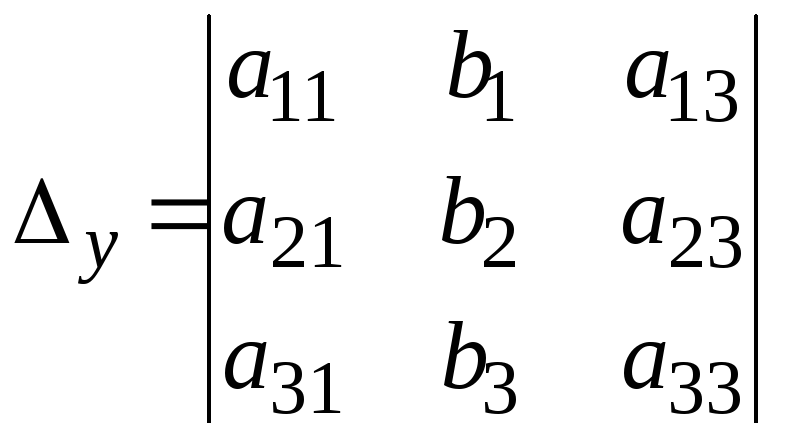
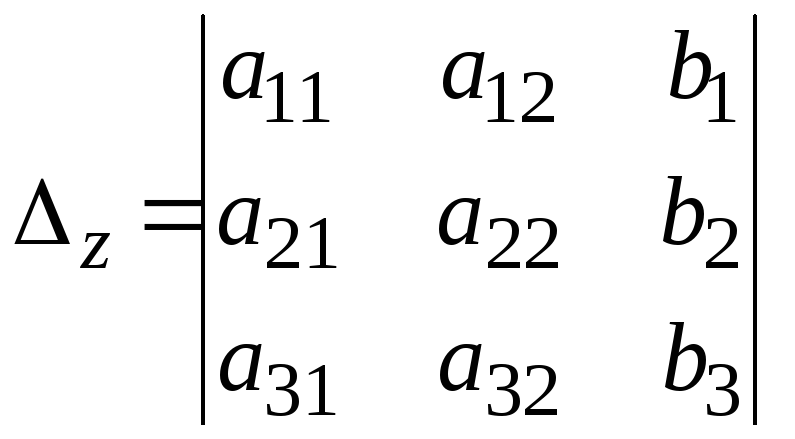
Тогда решение
системы находится по формулам Крамера

,

,

Следует
отметить, что система имеет единственное
решение
,
если главный определитель.Если же

и
=
0,=
0,=
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же

и
0,
или0,или0,
то система уравнений несовместна, то
есть решений не имеет.

Пример

Решить
систему уравнений методом Крамера:

Решение:

1)
Составим и вычислим главный определитель
системы, состоящий из коэффициентов
при неизвестных.

.

Следовательно,
система имеет единственное решение.

2)
Составим и вычислим вспомогательные
определители, заменяя соответствующий
столбец в 
столбцом из свободных членов.

По формулам Крамера
находим неизвестные:

,
,.

Сделаем проверку,
чтобы убедиться в правильности решения

,
т.е.
.

,
т.е.

,
т.е.

Ответ:
.

Пример

Решить
систему уравнений методом Крамера:

Решение:

1)
Составим и вычислим главный определитель
системы из коэффициентов при неизвестных:

.

Следовательно,
система не имеет единственного решения.

2)
Составим и вычислим вспомогательные
определители, заменяя соответствующий
столбец в 
столбцом из свободных членов:

.

,
,
следовательно, система несовместна.

Ответ:
система
несовместна.

Метод Гаусса

Метод
Гаусса состоит из двух этапов. Первый
этап заключается в последовательном
исключении переменных из уравнений
системы при помощи действий, не нарушающих
равносильности системы. Например,
рассмотрим два первых уравнения системы
(1).

(1)

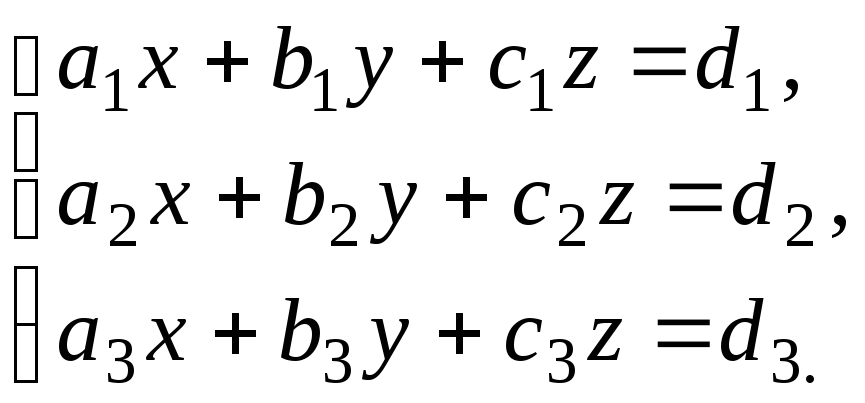
Необходимо
путем сложения этих двух уравнений
получить уравнение, в котором отсутствует
переменная
.
Умножим первое уравнение на,
а второе на ()
и сложим полученные уравнения

+

Заменим
коэффициент перед y,
z
и свободный член на
,исоответственно,
получим новую пару уравнений

Заметим,
что во втором уравнении отсутствует
переменная x.

Проведя
аналогичные действия над первым и
третьим уравнениями системы (1), а затем
над полученными в результате сложения
вторым и третьим уравнениями, преобразуем
систему (1) к виду

(2)

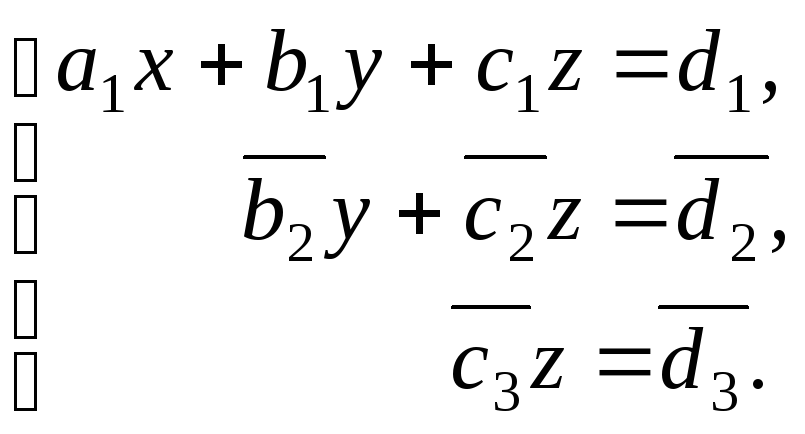
Такой
результат возможен, если система имеет
единственное решение. В этом случае
решение находится при помощи обратного
хода метода Гаусса (второй этап). Из
последнего уравнения системы (2) находим
неизвестную переменную z,
затем из второго уравнения находим y,
а x
соответственно из первого, подставляя
в них уже найденные неизвестные.

Иногда в результате
сложения двух уравнений суммарное
уравнение может принять один из видов:

А)
,
где.
Это означает, что решаемая система
несовместна.

Б)
,
то есть.
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.

Пример

Решить
систему методом Гаусса:

Решение:

Рассмотрим
следующий способ осуществления первого
этапа решения методом Гаусса. Запишем
три строки коэффициентов при неизвестных
и свободных членов, соответствующих
трем уравнениям системы. Свободные
члены отделим от коэффициентов
вертикальной линией, а под третьей
строкой проведем горизонтальную прямую.

Первую
строку, которая соответствует первому
уравнению системы, обведем – коэффициенты
в этом уравнении останутся неизменными.
Вместо второй строки (уравнения) надо
получить строку (уравнение), где
коэффициент при
равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент приравен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.

Все
описанные действия изображены в таблице
1 при помощи арифметических знаков и
стрелок. Обведенные в таблице строки
запишем снова в виде уравнений (3) и,
применив обратный ход метода Гаусса,
найдем значения переменных x,
y
и z.

Таблица 1

1	1	-2	6	*(-2)	*(-5)
2	3	-7	16
5	2	1	16
0	1	-3	4	*( 3)
0	-3	11	-14
0	0	2	-2

Восстанавливаем
систему уравнений, полученную в результате
наших преобразований:

(3)

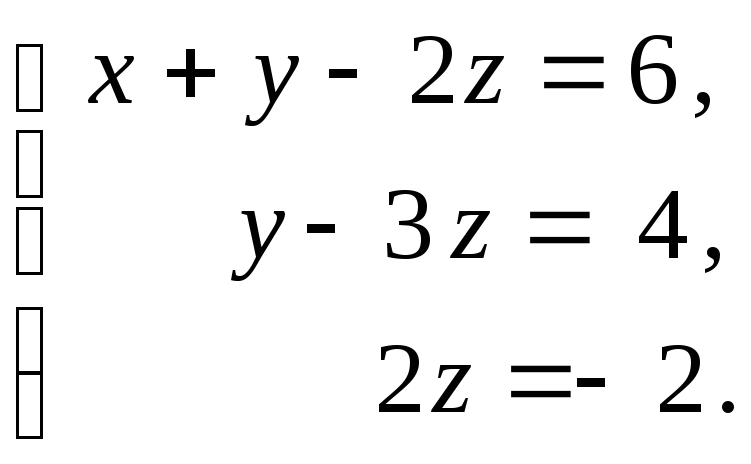
Обратный ход
метода Гаусса

Из
третьего уравнения
находим.

Во
второе уравнение системы
подставим найденное значение,
получимили.

Из
первого уравнения
,
подставляя уже найденные значения
переменных, получаем,
то есть.

Чтобы убедиться
в правильности решения, проверку
необходимо сделать во всех трех уравнениях
системы.

Проверка:

,
получим

,
получим

,
получим

значит, система
решена верно.

Ответ:
,,.

Пример

Решить
систему методом Гаусса:

Решение:

Порядок
действий в этом примере аналогичен
порядку в предыдущем примере, а конкретные
действия указаны в таблице 2.

Таблица2

2	2	1	1	*(-3)	*(-5)
3	5	-2	0	*2
5	3	6	-2	*2
0	4	-7	-3
0	-4	7	-9
0	0	0	-12

В
результате преобразований получим
уравнение вида
,
следовательно, заданная система
несовместна.

Ответ:
система
несовместна.

Пример

Решить
систему методом Гаусса:

Решение:

Таблица
3

1	2	-1	0	*(-2)	*(-4)
2	-1	3	1
4	3	1	1
0	-5	5	1	*(-1)
0	-5	5	1
0	0	0	0

В
результате преобразований получим
уравнение вида
,
которое исключается из рассмотрения.
Таким образом, имеем систему уравнений,
в которой число неизвестных 3, а число
уравнений 2.

Система
имеет бесчисленное множество решений.
Чтобы отыскать эти решения, введем одну
свободную переменную. (Число свободных
переменных всегда равно разности между
числом неизвестных и числом уравнений,
оставшихся после преобразования системы.
В нашем случае 3 – 2 = 1).

Пусть
– свободная переменная.

Тогда
из второго уравнения найдем
,
откуда,
а затем найдемx
из первого уравнения
или.

Таким
образом,
;;.

Сделаем
проверку в уравнениях, которые не
участвовали в нахождении
и,
то есть во втором и в третьем уравнениях
первоначальной системы.

Проверка:

или
,
получаем.

или
,
получаем.

Система
решена верно. Давая произвольной
постоянной
различные значения, будем получать
различные значенияx,
y
и z.

Ответ:

;;.

21

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ. К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x, при котором уравнения системы обращаются в тождества, называется решением системы,  a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B, соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

А теперь о том, как посчитать определитель. Например, определитель матрицы третьего порядка, который чаще всего встречается на практике, вычисляется по формуле:

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру,  на этом сайте.

А если система оказалась упорной и  не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы купить конспект. Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!