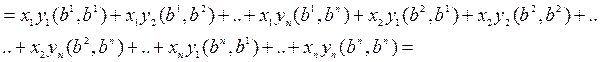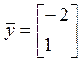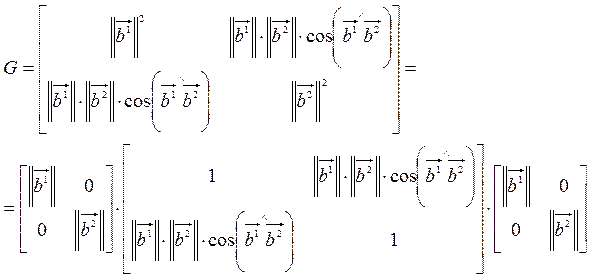Федеральное
агентство по образованию
Государственное
образовательное учреждение высшего
профессионального образования
Санкт-Петербургский государственный
горный институт им. Г.В.Плеханова
(технический
университет)
А.П. Господариков,
Г.А. Колтон,
С.А. Хачатрян
Ряды фурье. Интеграл
Фурье.
Операционное
исчисление
Учебно-методическое
пособие
САНКТ-ПЕТЕРБУРГ
2005
УДК 512 + 517.2 (075.80)
ББК 22.161.5
Г723
Учебно-методическое
пособие дает возможность получить
практические навыки анализа функций с
помощью разложения в ряд Фурье или
представления интегралом Фурье и
предназначено для самостоятельной
работы студентов дневной и заочной форм
обучения специальностей.
В пособии рассмотрены
основные вопросы операционного исчисления
и широкий класс технических задач с
применением основ операционного
исчисления.
Научный
редактор проф.
А.П. Господариков
Рецензенты:
кафедра высшей математики № 1
Санкт-Петербургского государственного
электротехнического университета;
доктор физ.-мат. наук В.М. Чистяков
(Санкт-Петербургский государственный
политехнический университет).
Господариков
А.П.
Г723.
Ряды Фурье. Интеграл Фурье. Операционное
исчисление: Учебно-методическое
пособие /
А.П. Господариков,
Г.А. Колтон,
С.А. Хачатрян;
Санкт-Петербургский государственный
горный институт (технический университет).
СПб,
2005. 102 с.
ISBN 5-94211-104-9
УДК
512 + 517.2 (075.80)
ББК
22.161.5
|
ISBN |
Санкт-Петербургский
институт им. Г.В.Плеханова, |
Введение
Из
теории Фурье известно, что при некотором
воздействии на физические, технические
и другие системы, его результат повторяет
форму начального входного сигнала,
отличаясь только масштабным коэффициентом.
Понятно, что на такие сигналы (их называют
собственными) система реагирует наиболее
простым образом. Если произвольный
входной сигнал есть линейная комбинация
собственных сигналов, а система линейна,
то реакция системы на этот произвольный
сигнал есть сумма реакций на собственные
сигналы. И поэтому полную информацию о
системе можно получить по «кирпичикам»
– откликам системы на собственные
входные сигналы. Так поступают, например,
в электротехнике, когда вводят частотную
характеристику системы (передаточную
функцию). Для наиболее простых линейных,
инвариантных во времени систем (например,
описываемых обыкновенными дифференциальными
уравнениями с постоянными коэффициентами)
в некоторых случаях собственными
функциями являются гармоники вида
.
Таким образом можно получить и результат
произвольного воздействия на систему,
если последний будет представлен в виде
линейной комбинации гармоник (в общем
случае, в виде ряда Фурье или интеграла
Фурье). Вот одна из причин, по которой в
теории и приложениях возникает потребность
применения понятия тригонометрического
ряда (ряда Фурье) или интеграла Фурье.
Глава 1. Ряды фурье
§ 1. Векторные пространства
Здесь
приведены краткие сведения из векторной
алгебры, необходимые для лучшего
понимания основных положений теории
рядов Фурье.
Рассмотрим
множество
геометрических векторов (векторное
пространство), для которого обычным
образом введены понятие равенства
векторов, линейные операции (сложение
и вычитание векторов, умножение вектора
на число) и операции скалярного умножения
векторов.
Введем
в пространстве
ортогональный базис, состоящий из трех
попарно ортогональных векторов
,
и
.
Произвольный векторявляется линейной комбинацией векторов
базиса:
.
(1.1)
Коэффициенты
i
(i = 1, 2, 3),
называемые координатами вектора
относительно базиса
,
могут быть определены следующим образом.
Скалярное произведение вектораи одного из векторов базиса
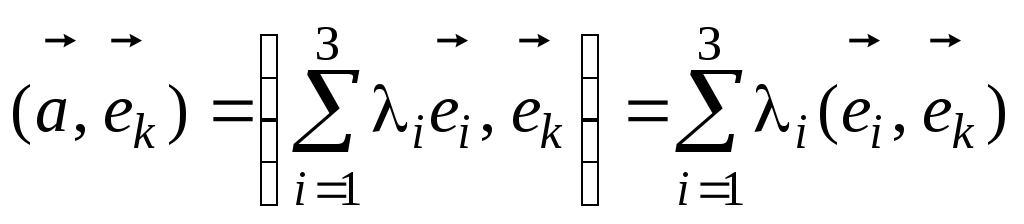
В
силу ортогональности базиса скалярные
произведения
при
,
следовательно, в правой части последнего
равенства отлично от нуля лишь одно
слагаемое, соответствующее,
поэтому,
откуда
,
(1.2)
где
.
Если
векторы
и
заданы своими координатами
и
,
то их скалярное произведение

Так
как при
скалярное
произведение,
то в двойной сумме отличны от нуля лишь
слагаемые с равными индексами, поэтому
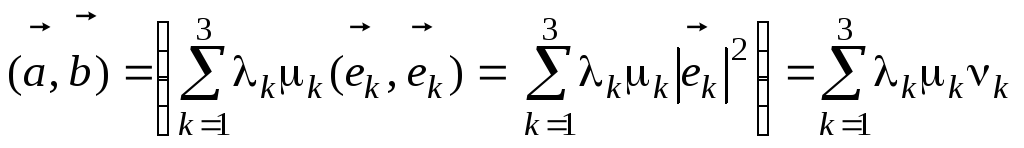
(1.3)
В
частности при
из (1.3) следует
.
(1.4)
§ 2. Скалярное произведение и норма функций
Обозначим
символом
множество
функций,
кусочно-непрерывных
на промежутке [a, b],
т.е. функций, имеющих на промежутке
[a, b]
конечное число точек разрыва первого
рода и непрерывных во всех остальных
точках этого промежутка.
Скалярным
произведением функций
называется число
.
Свойства
скалярного произведения функций
полностью
совпадают со свойствами скалярного
произведения векторов:
1.
.
2.
.
3.
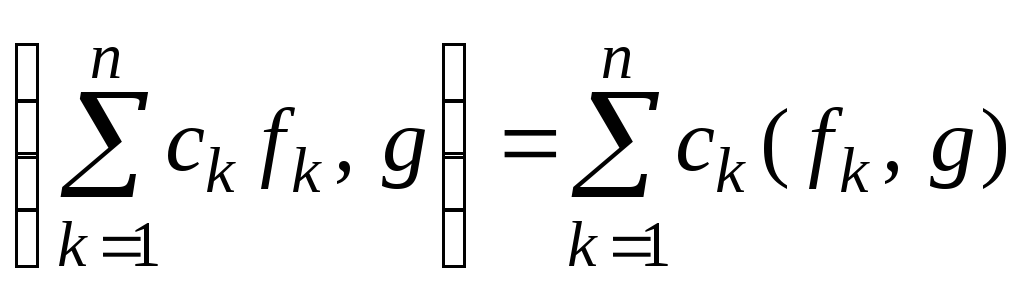
4.
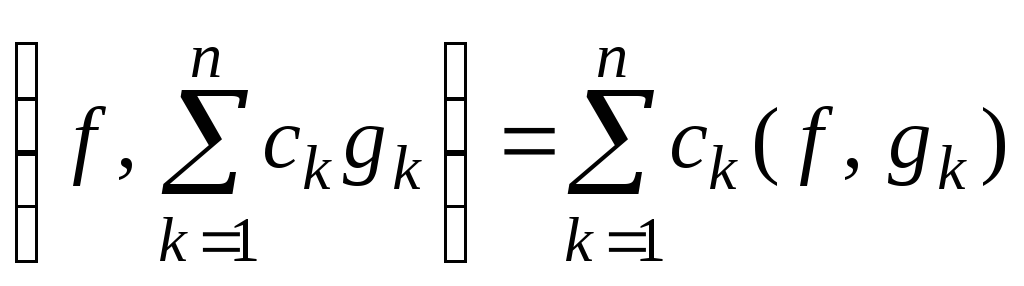
.
Таким
образом, скалярное произведение линейно
зависит от своих компонентов. Это
свойство называется билинейностью
скалярного произведения.
Функции
называются
ортогональными
на [a, b],
если
.
Нормой
функции
на промежутке
[a, b]
называется неотрицательное число
,
квадрат которого равен скалярному
произведению функции
на себя:
.
Свойства
нормы функции
во многом совпадают со свойствами модуля
вектора:
1.
.
2. Если
функция
непрерывна на [a, b]
и
,
то.
Так как,
то при
,
откуда
.
Дифференцируя последнее соотно- шение
пои применяя теорему Барроу, получим
и, сле-довательно,
.
3. теорема
косинусов
.
.
Следствие.
Если
,
то(теорема Пифагора).
4. Обобщенная
теорема Пифагора. Если
функции
(k =
= 1, 2, …, n)
попарно ортогональны на промежутке
,
то

Используя
свойство билинейности скалярного
произведения, получим
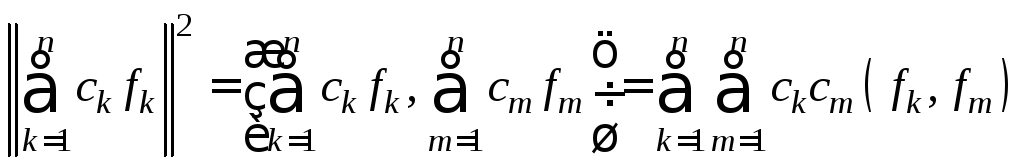
В
силу ортогональности функций
скалярные произведения
при
,
поэтому
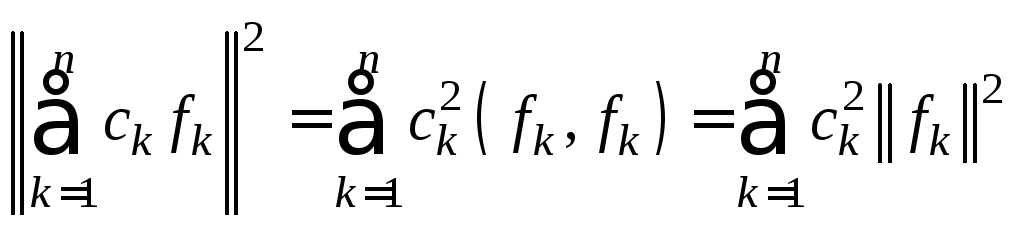
5. неравенство
Коши – Буняковского
,
или, что то же самое,
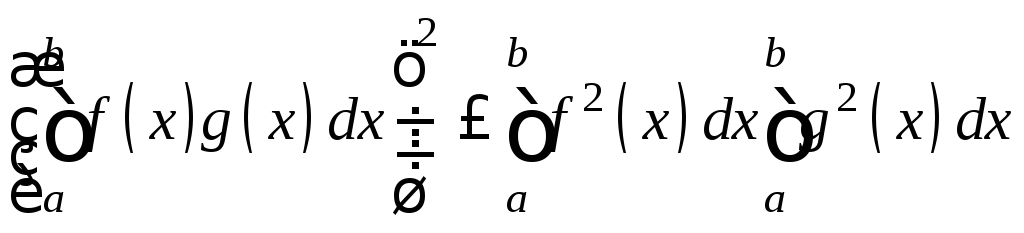
При
любых вещественных
.
Таким
образом, квадратный трехчлен в левой
части последнего не-равенства сохраняет
знак на всейвещественнойоси, следовательно,
его дискриминант
.
Упражнение 1. Доказать
свойства скалярного произведе-ния
функций 1-3.
Упражнение 2. Показать
справедливость следующих ут-верждений:
а) функция
ортогональна функциям
и
на промежутке
при любых целыхk
и m;
б) при
любых целых k
и m
функции
и
ортогональны
на промежутке;
в) функции
и
,
а такжеи
при
ортогональны на промежутках
и
;
г) функции
и
не ортогональны на промежутке
.
Упражнение 3. Используя
свойство нормы 5, доказать неравенство
треугольника
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
проверено. буква E смотрится странно
Определение 1. Пусть 



-
Симметричность:
для всех
;
-
Положительная определенность:
для всех
, и обращается в нуль, лишь если
.
Часто для скалярного произведения векторов 




Пример 1. На пространстве непрерывных функций ![$C^0[a,b]$ $C^0[a,b]$](http://www.algebraical.info/doku.php/lib/exe/fetch.php?cache=&media=latex%3Ae1e9b7f3bcdd494cb492a457e5b1f447.png)

Пример 2. На пространстве 




Определение 2. Евклидовым векторным пространством2) называется векторное пространство над полем 

Пример 3. Пространство 
Определение 3. Пусть 



Предложение 1 (Неравенство Коши-Буняковского). Для произвольных векторов 


Пример 4. В случае, когда евклидово пространство — это пространство непрерывных на отрезке ![$[a,b]$ $[a,b]$](http://www.algebraical.info/doku.php/lib/exe/fetch.php?cache=&media=latex%3Adf271723a9c6d83a83a2ff94f8e22b0b.png)

Определение 4. Векторы 


Студент
не посудина, которую надо заполнить, а факел, который надо зажечь.
Скалярное
произведение
1.
Определение
Скалярное произведение –
это функционал типа , т. е. любым векторам
ставится в соответствие пара
. (Аргументы – это векторы, значение
– число.)
–
функция, – преобразование,
– функционал
При
этом выполняются аксиомы:
1.
–
симметрия (коммутативность),
2.
–однородность.
В силу симметрии .
3.
– аддитивность. Следовательно,
, т. к.
.
4.
и
– неотрицательность.
Рассмотрим
примеры скалярных произведений в различных пространствах.
· Скалярное произведение в арифметическом
пространстве .
Определим скалярное произведение
следующим образом: 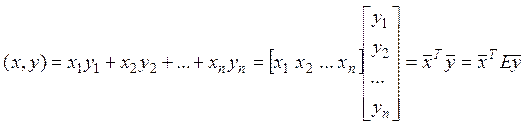
Очевидно, что все свойства скалярного
произведения выполнены.
Замечание. Можно ввести скалярное произведение следующим
образом , где
.
Какими свойствами должна обладать матрица ?
· Скалярное произведение в геометрическом
пространстве .
Определим скалярное произведение , но если только знаем длину, и какой
угол. Что такое длина?
3 свойство выполнено или нет – это большой вопрос.
, следовательно,
.
Т. к. проекция суммы есть сумма проекций:
· Скалярное произведение в пространстве функций .
Определим 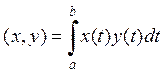
выполнены по свойствам интеграла, а значит, перед нами скалярное произведение.
2.
Неравенство Коши – Буняковского
Рассмотрим скалярное произведение в силу 4 свойства. Раскроем скобки,
используя свойства аддитивности и однородности: –
квадратный трехчлен относительно , который
неотрицателен для , следовательно,
.
или
– неравенство Коши – Буняковского,
которое еще записывается в виде: .
Неравенство выполняется в любом линейном пространстве,
т. к. выводится только из свойств скалярного произведения. Знак равенства в том
случае, если или
равны
, или
(
и
одного
направления).
Рассмотрим, какой вид примет данное неравенство в
конкретных линейных пространствах.
· В арифметическом пространстве .
– неравенство
Коши.
· В пространстве функций .
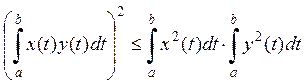
Буняковского (Шварца).
Этими неравенствами будем пользоваться и отдельно
доказывать не будем, т. к. мы доказали его для любого линейного пространства.
В некоторых учебниках можно найти вывод этих
неравенств отдельно для каждого пространства.
3.
Норма вектора и угол между
векторами
Норма элемента ,
обозначается , – это функционал типа
, который удовлетворяет свойствам:
1.
,
– неотрицательность,
2.
–
однородность,
3.
–
неравенство Минковского (треугольника).
Определим пока норму элемента следующим образом: . Очевидно, что свойства 1 и 2
выполняются. Проверим выполнение неравенства треугольника. По определению
(второе слагаемое неположительное по неравенству Коши
– Буняковского).
Норму ассоциируют как длину.
Линейное пространство со скалярным
произведением называют Евклидовым. Если определена норма, то нормированным.
Замечание. Норму можно
ввести и другими способами, главное, чтобы она удовлетворяла свойствам нормы.
Если норма появилась как следствие скалярного произведения, то норма называется
евклидовой.
Упражнение. Докажите, что
норма евклидова
.
Каким скалярным произведением она порождается?
Если
мы определим норму как , то неравенство
Коши – Буняковского примет вид: .
Определим угол между
векторами следующим образом
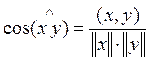
Определение
корректно, т. к. в силу неравенства Коши – Буняковского: 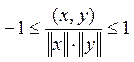
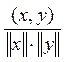
косинус некоторого угла.
Тогда
.
Примеры.
· :
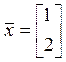
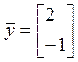
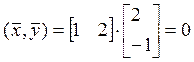
Вычислим угол: ,
, тогда
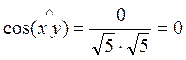
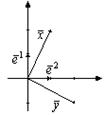
обозначаем как ):
, то
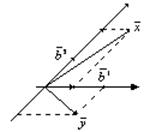
То , тогда
, где
–
некоторая матрица.
· .
,
. Найдем нормы:
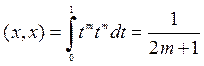
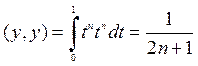
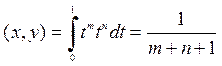
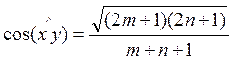
4. Ортогональность
Элементы
ортогональны,
если .
Т.
к. , то из определения следует что, либо
, либо
,
либо .
Примеры.
· .
,
.
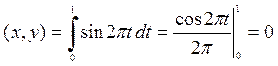
.
Вставить рисунок
· Типовая задача 1. Вычислить все элементы ,
ортогональные .
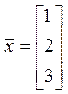
Обозначим 
.
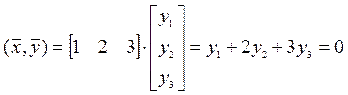
однородная система ранга 1.
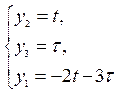
Т.
о. 
плоскость.
5. Типовые задачи
· Типовая задача 2. Нормировать элемент линейного пространства.
Т.
е. представить его в виде , где
– единичный вектор (орт), того же
направления, что и . Вычислим норму элемента
:
(т.
к. )
.,
т. е. .
Значит,
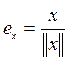
Пример.
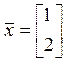
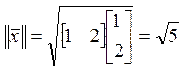
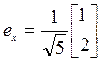
· Типовая задача 3. Вычислить
угол между элементами .
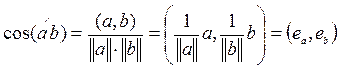
и от длин не зависит (как в геометрическом пространстве).
· Типовая задача 4. Вычислить
длину проекции элемента на направление
.
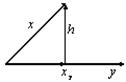
на
. Вектор
–
расстояние от вектора до
. Тогда
– коэффициенты Фурье.
· Типовая задача 5. Вычислить
проекцию элемента на направление
.
– проекция элемента
на направление
. Тогда
расстояние
от вектора до
.
Замечание. Проекция – это
вектор, длина проекции – это число.
6. Метрика линейного пространства
Пусть – линейное
пространство. Всякое линейное пространство можно задать как линейную оболочку
некоторой линейно независимой системы :
, тогда любой элемент линейного
пространства можно представить линейной комбинацией векторов . Пусть
,
.
Найдем скалярное произведение:
(раскроем,
используя свойства)
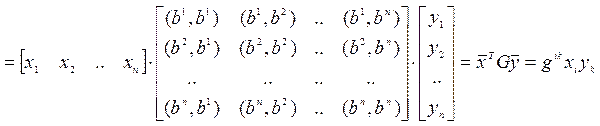
произведения.
– называется
матрицей Грама.
– это
арифметический объект. Он и называется тензором скалярного произведения или
метрическим тензором.
В тензорном виде: .
· Типовая задача 6. Вычислить
скалярное произведение.
.
Если
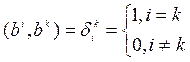
,
тогда .
Если
, то элементы
и
ортогональны.
Пример.
В
дан метрический тензор
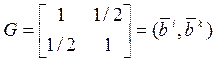
векторов 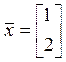
1)
в системе , 2) в системе
.
1).
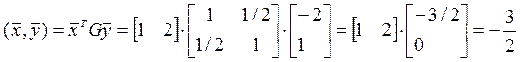
2).
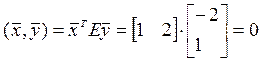
.
Зачем нужен базис? Чтобы сопоставить векторам их координаты,
т. е. арифметику (мы умеем работать с числами). Вводя матрицу , мы навязываем арифметическому
пространству геометрию.
Пример. Дан базис в
геометрическом пространстве:
Найти метрический тензор.
В
геометрическом пространстве длину угол можем замерить, если вооружимся линейкой
и транспортиром, тогда
–
разложение метрического тензора на нормы и углы.

 для всех
для всех  ;
; для всех
для всех  , и обращается в нуль, лишь если
, и обращается в нуль, лишь если  .
.