Скалярным
произведением векторов называется
число равное произведению длин этих
векторов на косинус угла между ними.
a*b=(a,b)=|a|*|b|*cosφ=|a|*праb=|b|*прba
1)
если угол осрый, то ab>0
2)если
угол тупой, то ab<0
3)
если угол прямой, то ab=0
Физический
смысл:
ω=|a|*|b|*cosφ=(a,b)
– работы силы а, точка приложения которой
перемещается из начала в b.
Свойства
скалярного произведения:
1)
переместительное свойство
ab=ba
2)
Сочетательное свойство относительно
скалярного множителя:
λ(ab)=a(λb)
3)
Распределительное свойство:
(α+β)ab=α(ab)+β(ab)
a(b+c)=ab+ac
4)
Скалярное произведение двух ортогональных
векторов равно нулю:
ab=0
5)
Скалярное произведение двух коллинеарных
векторов
ab=±|a|*|b|,
если a||b
Выражение
скалярного произведения через координаты
перемноженных векторов в декартовой
системе координат.
Теорема:
Если
векторы а={x1,y1,z1};
b={x2,y2,z2}
заданы декартовыми координатами, то
ab=x1*x2+y1*y2+z1*z2
(сумма попарных произведений одноименных
координат)
Док-во:
Составим
таблицу скалярного умножения базисных
векторов:
i*i=1
i*j=0 i*k=0
i*j=0
j*j=1
j*k=0
i*k=0
j*k=0 k*k=1
a*b=(x1*i+y1*j+z1*k)*(x2*i+y2*j+z2*k)=x1*x2*i*i+x1*y2*i*j+x1*z2*i*k+y1*j*x2*i+y1*y2*j*j+y1*j*z*k+z1*x2*k*i+y2*z1*j*k+z1*z2*k*k=x1*x2+y1*y2+z1*z2
(доказано)
Скалярный
квадрат:
a2=|a|2=ax2+ay2+az2
отсюда
следует формула для модуля
вектора.
Следствия:
1.
Необходимое и достаточное условие
ортогональности векторов является
равенство:
a|_b
↔ x1x2+y1y2+z1z2=0
2.
Угол φ между векторами определится
равенством:
cosφ=(x1x2+y1y2+z1z2)/
sqrt(x1^2+
y1^2
+z1^2)*
sqrt
(x2^2
+ y2^2+z2^2)
(ab=|a|*|b|*cosφ),
то cosφ=
3.
Если некоторая ось u
составляет с координатными осями углы
α,β,γ, то проекция произвольного вектора
s={x,y,z}
на эту ось определяется равенством
прus=xcosα+ycosβ+zcosγ
Док-во:
прus=(u,s)*1/|u|=(us=|u|*
прus)=(u/(u,s))=
xcosα+ycosβ+zcosγ
u/|u|={cosα,cosβ,cosγ}
2.4. Векторное произведение, его свойства, вычисление.
Векторным
произведением вектора a
на вектор b
называется вектор с=a
x
b.
который определяется следующими тремя
условиями:
1.
|a
x
b|=|a|*|b|*sinφ
2.
a|_c,
b|_c
вектор с ортогонален векторам a
и b
3.
вектор с направлен так, что векторы
a,b,c
образуют правую тройку.
(если
кратчайший поворот вектора а к вектору
b
осуществляется против часовой стрелки
– правая тройка.
i,j,k
– правая тройка.
Геометрические
свойства:
1.
Если a||b
↔ a
x
b=0
(необходимое и достаточное условие
коллинеарности)
sinφ=0
2.
Если a
и b
приведены к общему началу, то
S=|a|*|b|*sinφ=|a
x
b|
(площадь параллелограмма)
Sтр=1/2*Sпар=1/2*|a
x
b|
Алгебраические
свойства:
1.
а x
b=
-b
x
a
(меняется направленность тройки)
2.
Сочетательный закон по отношению к
умножению на скаляр
(λa)
x b= λ(a
x b)
(a
x λb)=
λ(a
x b)
3.
Распределительный закон относительно
умножения на сумму векторов
a
x (b+c) = a x b + a x c
(b+c)
x a= b x c + c x a
4.
a
x
a
=0
Выражение
векторного произведения через координаты
перемножаемых векторов в декартовой
системе координат.
Теорема:
Пусть
векторы а и b
заданы своими декартовыми координатами:
a={x1,y1,z1}
b={x2,y2,z2}
|i
j
k|
тогда
a
x
b=|x1
y1
z1|={
|y1
z1|,
— |x1
z1|,
|x1
y1|}
|x2 y2 z2| |y2
z2|
|x2
z2|,
|x2
y2|
Док-во:
Составим
таблицу векторного умножения базисных
векторов.
i
x i=0 j x i =-k k x i =j
i
x j=k j x j =0 k x j =-i
i
x k=-j j x k= i k x k=0
Воспользуемся
представлением a
и b
в декартовой системе координат:
а=x1*i+y1*j+z1*k
b=x2*i+y2*j+z2*k
a
x b= (x1*i+y1*j+z1*k)x(x2*i+y2*j+z2*k)=…=|y1 z1|i — |x1 z1|j +
|x1 y1|k
|y2
z2|
|x2
z2|
|x2
y2|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скалярное произведение
Скалярное произведение — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.
$$ c = |overline a||overline b|cos(theta )$$
Обычно для скалярного произведения векторов $overline a$ и $overline b$ используется одно из следующих обозначений:
$$ c= (overline a,overline b) = overline acdotoverline b$$
Скалярным произведением двух векторов $overline a$ и $overline b$ будет скалярная величина, равная сумме попарного произведения координат векторов $overline a$ и $overline b$.
Для плоскости:
Скалярное произведение векторов $overline a = (a_x, a_y)$ и $overline b = (b_x, b_y)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y $$
Для пространства:
Скалярное произведение двух векторов в пространстве $overline a = (a_x, a_y, a_z)$ и $overline b = (b_x, b_y, b_z)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y + a_z b_z $$
Векторное произведение
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Определение:
Векторным произведением вектора $overline a$ на вектор $overline b$ в трёхмерном евклидовом пространстве называется вектор $overline c$, удовлетворяющий следующим требованиям:
- длина вектора $overline c$ равна произведению длин векторов $overline a$ и $overline c$ на синус угла между ними (т. е. площади параллелограмма, образованного векторами $overline a$ и $overline b$
$$ | overline c| = | overline a| cdot | overline b|cdot sin (theta ),$$ - вектор $overline c$ ортогонален каждому из векторов $overline a$ и $overline b$;
- вектор $overline c$ направлен так, что тройка векторов $(overline a,overline b,overline c)$ является правой.
Понятие правой и левой тройки векторов:
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов $(overline a,overline b,overline c)$ в трёхмерном пространстве называется правой, если с конца вектора $overline c$ кратчайший поворот от вектора $overline a$ к вектору $overline b$ виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.
Название правой и левой тройки пошло от определения направления тройки с помощью руки человека:
Правая тройка. Указательный палец к среднему пальцу двигается против часовой стрелки.
Векторное произведение обозначают:
$$overline c = overline a times overline b = [overline a, overline b]$$
Получение координат вектора $overline c$:
Если два вектора $overline a$ и $overline {b}$ представлены в правом ортонормированном базисе координатами $ overline a=(a_x,a_y,a_z), overline b=(b_x,b_y,b_z)$, то их векторное произведение имеет координаты:
$$ overline a timesoverline b = (a_yb_z — a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x).$$
Для запоминания этой формулы удобно использовать мнемонический определитель:
$$overline a timesoverline b = begin{vmatrix}
i & j & k \
a_x & a_y & a_z \
b_x & b_y & b_z \
end{vmatrix}, $$
где $i=(1,0,0), j=(0,1,0), k=(0,0,1)$.
Псевдоскалярное произведение двух векторов
Псевдоскалярным (или косым) произведением векторов $overline{a}$ и $overline{b}$ на плоскости называют число
$$c = | overline a| cdot | overline b|cdot sin (theta ),$$
где $theta$ — угол вращения (против часовой стрелки) от $overline{a}$ к $overline{b}$. Приставка «псевдо» означает, что объект может менять или не менять знак при отражениях пространства.
Псевдоскалярное произведение обозначают так:
$$c = overline a wedge overline b.$$
Если хотя бы один из векторов нулевой, то полагают $overline a wedge overline b = 0$.
Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
С его помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.
Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является смешанное произведение.
Основные свойства:
- Линейность: $overline a wedge (lambda overline b + muoverline c ) = lambdaoverline awedgeoverline b + muoverline a wedge overline c$. Где $lambda, mu$ — произвольные вещественные числа.
- Антикоммутативность: $overline a wedgeoverline b = -overline bwedgeoverline a$.
- Ориентированная площадь треугольника ABC выражается формулой $S = (overline{AB}wedgeoverline{AC}) / 2$, а его площадь равна модулю этой величины.
- $overline a wedge overline b = 0$ — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости.
- Пусть заданы вектора $overline a = (a_1, a_2), overline b = (b_1, b_2)$. Тогда их псевдоскалярное произведение равно $overline a wedgeoverline b = a_1b_2 — a_2b_1$.
Использование в геометрических задачах
Пример 1. Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому достаточно посчитать косое произведение векторов $overline{P_1P_2}$ и $overline{P_1M}$ и по его знаку сделать вывод.
Пример 2. Определить, принадлежит ли точка отрезку.
Пусть точки $P_1(x_1, y_1), P_2(x_2, y_2)$ — концы заданного отрезка. Необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через $P_1, P_2$. Далее нужно определить лежит ли точка между точками $P_1$ и $P_2$. Для этого используем скалярное произведение векторов $overline{MP_1}, overline{MP_2}$. Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. $overline{P_1P_2} wedge overline{P_1M} = 0$ – косое произведение (точка лежит на прямой);
2. $(overline{MP_1}, overline{MP_2}) ≤ 0$ – скалярное произведение (точка лежит между $P_1$ и $P_2$).
Пример 3. Определить, пересекаются ли две прямые (прямые не совпадают).
Если прямые заданы точками $P_1(x_1, y_1), P_2(x_2, y_2), M_1(x_3, y_3), M_2(x_4, y_4)$, то условие их параллельности заключается в проверки косого произведения векторов $overline{P_1P_2}$ и $overline{M_1M_2}$: если оно равно нулю, то прямые параллельны, иначе — пересекаются.
Пример 4. Определить, пересекаются ли два отрезка.
Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Необходимо проверить, лежат ли концы каждого из отрезков по разные стороны относительного концов другого отрезка. Применим косое произведение векторов. Посмотрим на первый рисунок: $overline{P_1P_2}wedge overline{P_1M_2} * overline{P_1P_2}wedge overline{P_1M_1} < 0$ и $overline{M_1M_2}wedge overline{M_1P_1} * overline{M_1M_2}wedge overline{M_1P_2} < 0$. Важно обратить внимание на строгое неравенство, потому что возможен случай, при котором произведение равно нулю, но отрезки не пересекаются (отрезки лежат на одной прямой, но не имеют общих точек). Поэтому необходимо проверить, принадлежит ли хотя бы один конец каждого отрезка другому.
Еще примеры:
- https://foxford.ru/wiki/informatika/primenenie-skalyarnogo-i-vektornogo-proizvedeniya
- https://habr.com/en/post/147691/
План урока:
Угол между векторами
Понятие скалярного произведения векторов
Скалярное произведение в координатах
Определение перпендикулярности векторов и прямых
Вычисление угла между векторами
Свойства скалярного произведения
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.
Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.
На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:
Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что
Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:
Ответ: а) 45°; б) 90°; в) 135°.
Понятие скалярного произведения векторов
Большое распространение в науке получила математическая операция, именуемая скалярным произведением векторов. В геометрии оно помогает находить угол между векторами, а в физике вычислять некоторые физические величины. В рамках школьной программы его используют для нахождения работы, совершенной той или иной силой. В рамках же более сложных дисциплин, с которыми мало кто сталкивается, оно применяется в квантовой механике и специальных разделах математики – тензорной алгебре, теории многообразий и т. п. Ввел его в науку Уильям Гамильтон в 1846 г, который разрабатывал теорию особых чисел – кватерионов. Они, кстати, используются компьютерами для расчетов трехмерной графики в играх и других приложениях.
Прежде, чем мы научимся применять на практике скалярное произведение, сначала сформулируем правило, позволяющее вычислить его.
Например, пусть есть вектора a и b, причем даны их длины:
Угол между a и b тоже известен и составляет 60°, это записывается таким образом:
Задание. Вычислите скалярное произведение векторов d и f, если их длины составляют 6 и 10 соответственно, а угол между векторами равен 45°.
Решение. Просто подставляем числа из условия в формулу:
Задание. АВС – равносторонний треугольник со стороной 4. Каково скалярное произведение векторов АВ и АС?
Решение. Все углы в равностороннем треугольнике равны 60°, поэтому и угол между АВ и АС также составляет 60°.
Ответ: 8.
Напомним, что косинус, взятый от острого угла – это положительная величина, а косинус тупого угла – это отрицательное число. У прямого же угла косинус равен нулю. Это означает, что по знаку скалярного произведения можно определить тип угла между векторами.
Часто скалярное произведение применяется в физике. Например, с его помощью рассчитывается работа, совершаемая силой при перемещении того или иного тела. И сила, и перемещение – это векторные величины. Чтобы найти работу силы, надо скалярно перемножить вектора силы и перемещения:
Эта формула отражает физический смысл скалярного произведения.
Задание. Под воздействием силы 10Н тело переместилось в горизонтальном направлении на 3 метра. При этом сила образует угол 60° с направлением перемещения тела. Какую работу совершила сила?
Решение.
Скалярное произведение в координатах
Оказывается, что для перемножения векторов достаточно знать только их координаты.
Докажем эту формулу. Сначала рассмотрим случай, когда один из перемножаемых векторов, например a, является нулевым. Тогда у него нулевая длина и нулевые координаты:
Теперь рассмотрим случай, когда оба перемножаемых вектора ненулевые. Тогда отложим их от некоторой точки О и, если вектора неколлинеарны, то мы получим ∆ОАВ:
Для частных случаев, когда a и b коллинеарны (то есть либо сонаправлены, либо противоположно направлены), эта формула также справедлива. Если aи b сонаправлены, то угол α принимается равным нулю (и cosα = 1):
Если же a и b направлены противоположно, то α = 180° (и cosα = – 1):
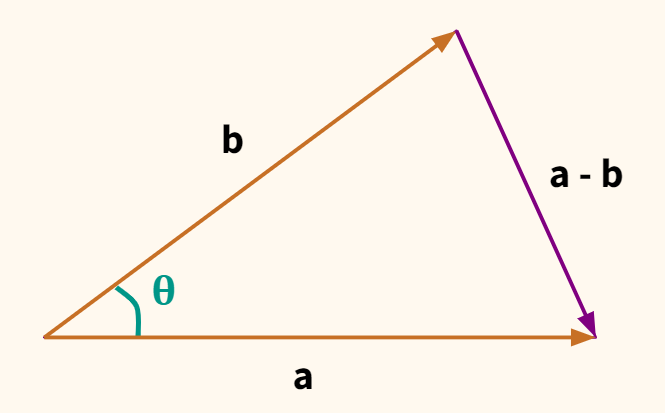
Итак, мы убедились, что в любой ситуации формула (1) справедлива. При этом вектор АВ можно представить как разность a и b:
Если вектор а имеет координаты {x1; у1}, а координаты b– это {x2; у2},то координаты их разности a – b будут записываться в виде {х1 – х2;у1 – у2}. С учетом этого (2) примет вид
В результате нам удалось доказать формулу скалярного произведения через координаты:
Задание. Перемножьте скалярно вектораa и b, если определены их координаты:
Ответ: а) 23; б) 0; в) 5.
Определение перпендикулярности векторов и прямых
Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.
Задание. Проверьте, являются ли перпендикулярными вектора:
Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:
Ответ: а) да; б) нет; в) да; г) нет.
Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?
Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:
Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:
Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).
Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.
Ответ: перпендикулярны.
Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями
Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:
Полученный ноль показывает, что исходные прямые перпендикулярны.
Ответ: перпендикулярны.
В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.
Докажем это утверждение. Пусть две прямые заданы уравнениями
Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:
Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:
В результате мы получили доказываемую нами формулу.
Задание. Проверьте, какие из этих пар прямых перпендикулярны:
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.
Вычисление угла между векторами
Мы научились по координатам векторов определять, перпендикулярны ли они. Однако в более общем случае можно рассчитать угол и между двумя неперпендикулярными векторами.
В самом деле, по известным координатам векторов легко как рассчитать длину каждого из них, так и скалярно перемножить вектора. Тогда из формулы скалярного произведения можно выразить значение косинуса угла между векторами:
Зная же косинус, можно рассчитать и сам угол, используя специальные таблицы либо функцию арккосинуса на калькуляторе.
Задание. Вычислите угол между векторами а{3; 4} и b{8; 15}.
Решение. Сначала рассчитываем длины векторов:
Задание. Точки А(2; 8), В(– 1; 5) и С(3; 1) соединили отрезками и получили ∆АВС. Вычислите угол ∠А в ∆АВС.
Решение.∠А данного треугольника представляет собой угол между двумя векторами АВ и АС. Вычислим координаты этих векторов:
Осталось лишь с помощью калькулятора найти сам ∠А:
Свойства скалярного произведения
Существует несколько важных свойств скалярного произведения. Эти свойства очень схожи с законами алгебры, которые используются при работе с обычными числами.
Переместительный закон легко доказать, опираясь только на определение операции скалярного произведения:
Задание. Известно, что угол между векторами a и с составлет 60°, так же как и угол между векторами b и с. Определены и длины векторов:
Задание. Найдите скалярное произведение векторов p и q, если
Решение. Сначала надо перемножить вектора и раскрыть при этом скобки также, как они раскрываются при перемножении обычных чисел:
Примечание. Иногда скалярное произведение вектора на самого себя именуют скалярным квадратом.
Тогда выражение (1) примет вид:
В сегодняшнем уроке мы узнали, что такое скалярное произведение. Оно имеет много приложений в физике и других науках, в частности, с его помощью вычисляется работа. В геометрии оно помогает вычислять углы между векторами, а значит, и между прямыми. В будущем, при более углубленном изучении геометрии, вы узнаете о существовании других типов произведений векторов – векторном и смешанном.
Все курсы > Линейная алгебра > Занятие 1
Материалы по линейной алгебре используют определения и примеры следующих курсов:
- 3Blue1Brown⧉
- Khan Academy: Linear Algebra⧉
- Linear Algebra⧉, PCA⧉, ICL
- Linear Algebra⧉, MIT
- Matrix Methods for Data Analysis and Machine Learning⧉, MIT
- Matrix Algebra for Engineers⧉
На первом занятии мы более подробно рассмотрим понятие вектора и векторного пространства.
Ноутбук к сегодняшнему занятию⧉
Понятие вектора
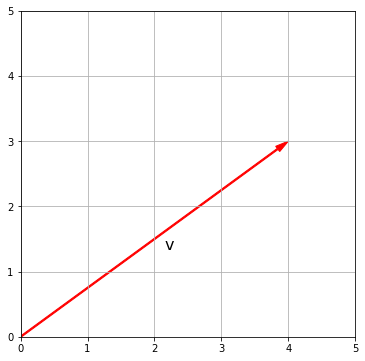
Вектор (vector) — это направленный отрезок, и для нас будет важно, что любой вектор обладает длиной (magnitude) и направлением (direction). Например, возьмем вот такой двумерный вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
На курсе мы будем обозначать векторы полужирной строчной буквой, например $textbf{v}$, а матрицы заглавной буквой, например, А.
Вектор $textbf{v}$ удобно изобразить на координатной плоскости, исходящим из начала координат.
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([0, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Добавлю, что вектор — частный случай матрицы. В случае вектор-столбца речь идет о матрице размерностью n x 1. В случае вектор-строки — 1 x n. Вектор $textbf{v}$ — это матрица 2 х 1.
Операции над векторами
Сложение векторов
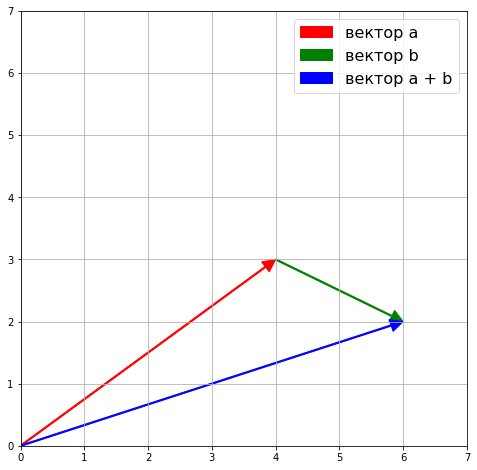
Складывать векторы очень несложно. Достаточно сложить их компоненты или координаты.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + begin{bmatrix} 2 \ -1 end{bmatrix} = begin{bmatrix} 6 \ 2 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, —1]) a_plus_b = a + b a_plus_b |
Графически, если поставить начало второго вектора в конец первого, сложение можно представить как расстояние от начала первого вектора до конца второго. Своего рода путь, пройденный двумя векторами.
|
ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_a_plus_b = ax.arrow(0, 0, a_plus_b[0], a_plus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b, arrow_a_plus_b], [‘вектор a’, ‘вектор b’, ‘вектор a + b’], prop = {‘size’: 16}) plt.show() |
Сложение векторов ассоциативно $textbf{a} + textbf{b} = textbf{b} + textbf{a}$.
Умножение на скаляр
Умножение на скаляр просто удлиняет или укорачивает вектор.
$$ 2 cdot textbf{v} = 2 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} 8 \ 6 end{bmatrix} $$
|
v = np.array([4, 3]) double_v = 2 * v double_v |
|
ax = plt.axes() plt.xlim([0, 10]) plt.ylim([0, 10]) plt.grid() ax.arrow(0, 0, double_v[0], double_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘2v’, xy=(double_v[0], double_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Умножение на отрицательное число не только удлиняет или укорачивает вектор, но и переворачивает его направление.
$$ -0,5 cdot textbf{v} = -0,5 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -2 \ -1,5 end{bmatrix} $$
|
v = np.array([4, 3]) neg_half_v = —0.5 * v neg_half_v |
|
ax = plt.axes() plt.xlim([—5, 5]) plt.ylim([—5, 5]) plt.grid() ax.arrow(0, 0, neg_half_v[0], neg_half_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-0.5v’, xy=(neg_half_v[0], neg_half_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Очевидно, что умножение на −1 просто переворачивает направление вектора, но не меняет его длины.
$$ -1 cdot textbf{v} = -1 cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} -4 \ -3 end{bmatrix} $$
|
v = np.array([4, 3]) neg_one_v = —1 * v neg_one_v |
|
ax = plt.axes() plt.xlim([—5, 5]) plt.ylim([—5, 5]) plt.grid() ax.arrow(0, 0, neg_one_v[0], neg_one_v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.annotate(‘-v’, xy=(neg_one_v[0], neg_one_v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0], v[1]), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) plt.show() |
Вычитание и деление на число
Вычитание векторов можно представить как сумму первого вектора со вторым вектором, умноженным на −1.
$$ begin{bmatrix} 4 \ 3 end{bmatrix} + left( -1 cdot begin{bmatrix} 2 \ -1 end{bmatrix} right) = begin{bmatrix} 2 \ 4 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([2, —1]) b_neg = —1 * b a_minus_b = a + b_neg b_neg, a_minus_b |
|
(array([-2, 1]), array([2, 4])) |
Графически мы сначала находим вектор $textbf{-b}$ (зеленая стрелка), а затем прибавляем его к вектору $textbf{a}$ (красная стрелка).
|
plt.figure(figsize = (8, 8)) ax = plt.axes() plt.xlim([0, 7]) plt.ylim([0, 7]) plt.grid() arrow_a = ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) arrow_b_neg = ax.arrow(a[0], a[1], b_neg[0], b_neg[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) arrow_b = ax.arrow(a[0], a[1], b[0], b[1], width = 0.0001, head_width = 0.1, head_length = 0.1, length_includes_head = True, fc = ‘black’, ec = ‘black’, linestyle = ‘—‘) arrow_a_minus_b = ax.arrow(0, 0, a_minus_b[0], a_minus_b[1], width = 0.02, head_width = 0.2, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’) plt.legend([arrow_a, arrow_b_neg, arrow_b, arrow_a_minus_b], [‘вектор a’, ‘вектор -b’, ‘вектор b’, ‘вектор a+(-b)’], prop = {‘size’: 16}) plt.show() |
Остается добавить, что деление вектора на число, это всего лишь умножение на обратное число (multiplicative inverse). Разделим вектор $textbf{v}$ на семь.
$$ frac{textbf{v}}{7} = begin{bmatrix} 4 \ 3 end{bmatrix} cdot frac{1}{7} = begin{bmatrix} frac{4}{7} \ frac{3}{7} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/7) |
|
array([0.57142857, 0.42857143]) |
Тот факт, что мы выразили вычитание через сложение и умножение на скаляр, а деление через умножение на обратное число позволило нам остаться в пределах операций сложения и умножения на скаляр.
Видео про векторы⧉.
Длина вектора
Длину или норму вектора (norm, length, magnitude or size of a vector) рассчитать не сложно, достаточно вспомнить теорему Пифагора. Снова возьмем вектор $textbf{v}$
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix} $$
|
v = np.array([4, 3]) ax = plt.axes() plt.xlim([0, 5]) plt.ylim([—0.01, 5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.hlines(y = 0, xmin = 0, xmax = 4, linewidth = 3, color = ‘b’, linestyles = ‘—‘) ax.vlines(x = 4, ymin = 0, ymax = 3, linewidth = 3, color = ‘g’, linestyles = ‘—‘) plt.show() |
Как видно на графике, вектор $textbf{v}$, смещение вдоль оси x и смещение вдоль оси y образуют прямоугольный треугольник. Значит, длина вектора (гипотенуза) равна квадратному корню из суммы квадратов смещений (катетов или в нашем случае координат).
$$ ||textbf{v}|| = sqrt{4^2 + 3^2} = sqrt{25} = 5 $$
Для n-мерного вектора ничего не меняется.
$$ ||textbf{v}|| = sqrt{v_1^2 + v_2^2 + dots + v_n^2} $$
Например, найдем длину трехмерного вектора $textbf{w}$.
$$ textbf{w} = begin{bmatrix} 6 \ 3 \ 2 end{bmatrix} rightarrow ||textbf{w}|| = sqrt{6^2 + 3^2 + 2^2} = sqrt{49} = 7 $$
Единичный вектор
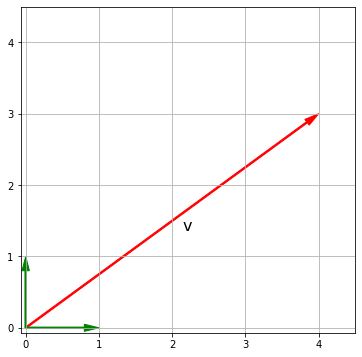
Вектор с длиной, равной единице, называют единичным вектором (unit vector). Примерами единичных векторов, с которыми мы будем часто встречаться в пространстве $ R^2 $, являются следующие два вектора
$$ hat{i} = begin{bmatrix} 1 \ 0 end{bmatrix}, hat{j} = begin{bmatrix} 0 \ 1 end{bmatrix} $$
Единичный вектор принято обозначать строчной буквой с знаком циркумфлекса, «крышечки» (hat).
Проверим, равна ли их длина единице.
$$ ||hat{i}|| = sqrt{1^2 + 0^2} = sqrt{1} = 1, ||hat{j}|| = sqrt{0^2 + 1^2} = sqrt{1} = 1 $$
Интересно, что с помощью векторов $ hat{i}, hat{j} $ можно выразить любой другой вектор в $ R^2 $. Например, вектор $textbf{v}$ можно представить как
$$ 4 begin{bmatrix} 1 \ 0 end{bmatrix} + 3 begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 4 \ 3 end{bmatrix} rightarrow 4hat{i} + 3 hat{j} $$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
v = np.array([4, 3]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, v[0], v[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) plt.annotate(‘v’, xy=(v[0]/2, v[1]/2), xytext=(10, —10), textcoords=‘offset points’, fontsize = 16) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Это обстоятельство нам пригодится в будущем.
Нормализация вектора
Длина нормализованного вектора равна единице. Для того чтобы нормализовать вектор, достаточно разделить вектор на его длину. Создадим единичный вектор $hat{v}$ для вектора $textbf{v}$.
$$ hat{v} = frac{textbf{v}}{||textbf{v}||} = frac{1}{5} cdot begin{bmatrix} 4 \ 3 end{bmatrix} = begin{bmatrix} frac{4}{5} \ frac{3}{5} end{bmatrix} $$
|
v = np.array([4, 3]) v * (1/np.linalg.norm(v)) |
Скалярное произведение
Важной операцией над векторами является уже знакомое нам скалярное произведение (dot product). В качестве напоминания того, как работает скалярное произведение приведем несложный пример. Пусть даны два вектора $textbf{v}$ и $textbf{w}$.
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 2 \ 1 end{bmatrix} $$
Найдем их скалярное произведение.
$$ textbf{v} cdot textbf{w} = 4 cdot 2 + 3 cdot 1 = 11 $$
Как вы видите, мы перемножаем компоненты векторов и складываем получившиеся произведения.
Скалярное произведение как длина вектора
Интересно, что корень из скалярного произведения вектора на самого себя есть его длина.
$$ sqrt{ textbf{v} cdot textbf{v} } = sqrt{4 cdot 4 + 3 cdot 3 } = sqrt{ 4^2 + 3^2 } = sqrt{25} = 5 $$
|
v = np.array([4, 3]) np.sqrt(v.dot(v)) |
Угол между векторами
Помимо этого скалярное произведение определяется как произведение длин векторов на косинус угла между ними.
$$ mathbf a cdot mathbf b = ||a|| cdot ||b|| cdot cos(theta) $$
Именно это свойство привело нас к расчету косинусного расстояния между векторами.
$$ cos(theta) = frac{mathbf a cdot mathbf b}{||a|| cdot ||b||} $$
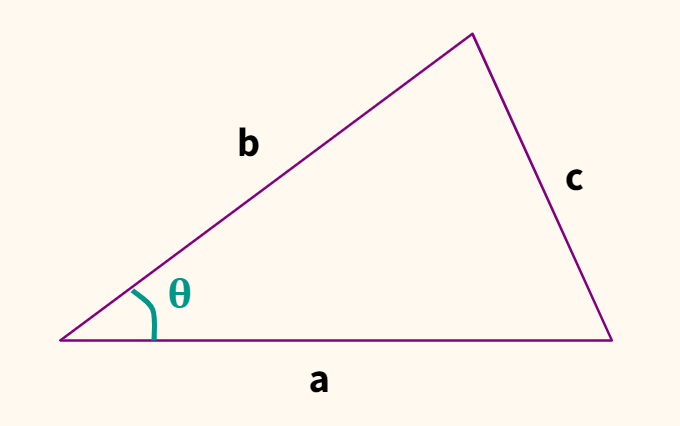
Выведем эту формулу. Для начала вспомним теорему косинусов.
$$ c^2 = a^2 + b^2-2ab cdot cos(theta) $$
Теперь представим, что у нас не стороны треугольника, а векторы. Если сторону а обозначить как вектор $ textbf{a} $, сторону b — как вектор $ textbf{b} $, то сторона с станет разностью между $ textbf{a} $ и $ textbf{b} $. Чтобы убедиться в этом, найдите $ textbf{-b} $ и приставьте его к окончанию $ textbf{a} $.
Выразим теорему косинусов через длины векторов.
$$ || a-b ||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Помня, что длина есть скалярное произведение вектора на самого себя, мы можем выразить левую часть $ || a-b || $ как
$$ (a-b)(a-b) = a cdot a-a cdot b-b cdot a + (-b) cdot (-b) = ||a||^2-2ab + ||b||^2 $$
Поместим результат в исходное выражение.
$$ ||a||^2-2ab + ||b||^2 = ||a||^2 + ||b||^2-2 cdot ||a|| cdot ||b|| cdot cos(theta) $$
Сократив подобные члены получим
$$ a cdot b = ||a|| cdot ||b|| cdot cos(theta) $$
Выводы. Из тригонометрии мы помним, что косинус 90 градусов равен нулю. Как следствие, скалярное произведение перпендиклярных (правильнее сказать ортогональных (orthogonal)) векторов $ textbf{a} perp textbf{b} $ равно нулю.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(90) = 0 $$
Очевидно, что если угол между двумерными векторами меньше 90 градусов, косинус, а значит и скалярное произведение положительны. В противном случае — отрицательны. Для n-мерных векторов положительное скалярное произведение говорит, что они в целом смотрят в одну строну, отрицательное — противоположные.
Для коллинеарных (сонаправленных) векторов скалярное произведение равно произведению их длин, потому что косинус нуля равен единице.
$$ a cdot b = ||a|| cdot ||b|| cdot cos(0) = ||a|| cdot ||b|| $$
Добавлю, что если $ textbf{a} $ и $ textbf{b} $ — единичные векторы, то косинус угла между векторами просто равен его их скалярному произведению.
$$ cos(theta) = a cdot b $$
Рассчитаем косинусное расстояние для векторов
$$ textbf{v} = begin{bmatrix} 4 \ 3 end{bmatrix}, textbf{w} = begin{bmatrix} 1 \ 7 end{bmatrix} $$
|
a = np.array([4, 3]) b = np.array([1, 7]) numerator = np.dot(a, b) aLen = np.linalg.norm(a) bLen = np.linalg.norm(b) denominator = aLen * bLen cosine = numerator / denominator angle = np.arccos(cosine) * 360/2/np.pi cosine, angle |
|
(0.7071067811865475, 45.00000000000001) |
|
from scipy.spatial import distance 1 — distance.cosine([4, 3], [1, 7]) |
Внешнее произведение
Под внешним произведением (outer product) понимается умножение вектор-столбца на вектор-строку по обычным правилам матричного умножения. Результатом такого произведения будет матрица, а не число, как в случае скалярного произведения.
Ортогональность векторов
Еще раз продемонстрируем, почему если векторы ортогональны, их скалярное произведение будет равно нулю. Возьмем три вектора, образовывающих прямоугольный треугольник.
Тогда, по теореме Пифагора,
$$ || mathbf x ||^2 + || mathbf y ||^2 = || mathbf x + mathbf y ||^2 $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = (mathbf x + mathbf y)^T (mathbf x + mathbf y) $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + mathbf x^T mathbf y + mathbf y^T mathbf x $$
$$ mathbf x^T mathbf x + mathbf y^T mathbf y = mathbf x^T mathbf x + mathbf y^T mathbf y + 2 mathbf x^T mathbf y $$
$$ mathbf 0 = 2 mathbf x^T mathbf y $$
$$ mathbf x^T mathbf y = mathbf 0 $$
Проекция вектора на вектор
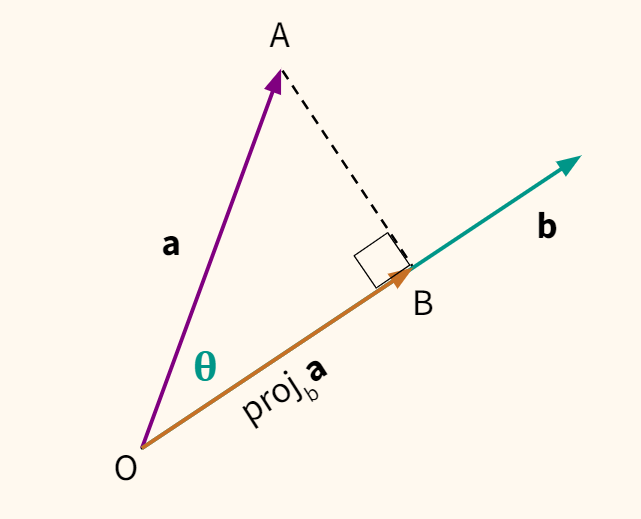
Подойдем к скалярному произведению с другой стороны. Рассмотрим два вектора $ textbf{a} $ и $ textbf{b} $ и найдем проекцию первого вектора на второй.
Проекция через угол между векторами
Говоря неформально, проекцией вектора $ textbf{a} $ на вектор $ textbf{b} $ будет такой участок вектора $ textbf{b} $, что расстояние от точки A до точки B минимально. Минимальным оно будет, если угол OAB будет равен 90 градусов. Получается прямоугольный треугольник. Найдем отрезок OB.
$$ cos(theta) = frac {OB}{OA} = frac {OB}{||a||} rightarrow OB = ||a|| cdot cos(theta) $$
Выразим то же самое через формулу скалярного произведения, заменив $||a|| cdot cos(theta) $ на OB.
$$ b cdot a = ||b|| cdot ||a|| cdot cos(theta) rightarrow b cdot a = ||b|| cdot OB $$
Так мы нашли длину проекции OB. Ее называют числовой или скалярной проекцией (scalar projection).
$$ frac{b cdot a}{||b||} = ||a|| cdot cos(theta) = OB $$
Более того, если длина вектора $ textbf{b} $ равна единице, то длина проекции OB просто равна скалярному произведению.
$$ ||b|| = 1 rightarrow b cdot a = OB $$
Это объясняет, почему скалярное произведение еще называют projection product.
Очевидное и тем не менее интересное примечание. Обратите внимание на связь понимания скалярного произведения как проекции одного вектора на другой и произведения длин векторов на косинус угла между ними. Если векторы перпендикулярны, проекция одного вектора на другой равна нулю, а значит и произведение проекции второго вектора на первый равно нулю.
Предположим, нас интересует не только длина проекции, но и ее направление. В этом случае говорят про векторную проекцию (vector projection).
Она выражается как произведение нормализованного вектора $ textbf{b} $ на длину проекции (то есть скалярную проекцию) OB.
$$ proj_mathbf{b} textbf{a} = OB cdot hat{b} $$
Перепишем OB через скалярное произведение, а $hat{b}$ через частное вектора $ textbf{b} $ на его длину.
$$ proj_mathbf{b} textbf{a} = frac{b cdot a}{||b||} cdot frac{b}{||b||} $$
Таким образом, можно сказать, что векторная проекция показывает, длину вектора $ textbf{a} $ в направлении вектора $ textbf{b} $.
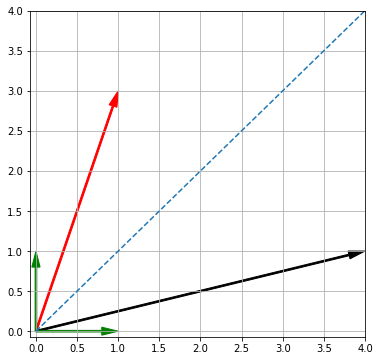
Пример. Возьмем два вектора a и b и найдем вначале скалярную, затем векторную проекцию вектора a на вектор b.
|
a = np.array([3, 4]) b = np.array([1, 1]) scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b |
|
vector_proj_a_on_b = scalar_proj_a_on_b * (b / np.linalg.norm(b)) vector_proj_a_on_b |
|
a = np.array([3, 4]) b = np.array([1, 1]) proj = np.array([3.5, 3.5]) ax = plt.axes() plt.xlim([—0.07, 4.5]) plt.ylim([—0.07, 4.5]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, proj[0], proj[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) plt.show() |
Матрица проекции
Векторную проекцию можно выразить с помощью матрицы проекции $P$.
$$ proj_mathbf{b} textbf{a} = P cdot mathbf a = frac{mathbf b mathbf b^T}{mathbf b^T mathbf b} cdot mathbf a $$
В знаменателе находится скалярное произведение и результатом умножения будет число. В числителе — внешнее произведение и результатом будет матрица. Найдем внешнее произведение из примера выше.
|
b_bT = np.outer(b, b) b_bT |
Найдем скалярное произведение.
Создадим матрицу проекции $P$ и умножим ее на вектор $mathbf a$.
Симметрия скалярного произведения
Продемонстрируем с точки зрения проекции, почему $a cdot b = b cdot a $. Возьмем два вектора a и b.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
a = np.array([1, 3]) b = np.array([4, 1]) i = np.array([1, 0]) j = np.array([0, 1]) ax = plt.axes() plt.xlim([—0.07, 4]) plt.ylim([—0.07, 4]) plt.grid() ax.arrow(0, 0, a[0], a[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’) ax.arrow(0, 0, b[0], b[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘k’, ec = ‘k’) ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’) ax.plot([0, 4], [0, 4], linestyle = ‘dashed’) plt.show() |
Выше мы сказали, что $ a cdot b = OB cdot ||b|| $. То есть скалярное произведение вектора a на вектор b равно произведению проекции a на b, умноженной на длину вектора b.
Продемонстрируем, что произведение проекции вектора a на вектор b, умноженное на длину вектора b, равно произведению проекции вектора b на вектор a, умноженному на длину вектора a.
$$ proj_ba times || b || = proj_ab times || a || $$
|
scalar_proj_a_on_b = np.dot(a, b) / np.linalg.norm(b) scalar_proj_a_on_b * np.linalg.norm(b) |
|
scalar_proj_b_on_a = np.dot(b, a) / np.linalg.norm(a) scalar_proj_b_on_a * np.linalg.norm(a) |
|
np.dot(a, b), np.dot(b, a) |
Видео про скалярное произведение векторов⧉.
Векторное произведение
Векторное произведение (cross product) задано только в трехмерном пространстве. Результатом такого произведения будет вектор, перпендикулярный каждому из исходных векторов. Приведем иллюстрацию из Википедии⧉.
Математически векторное произведение задается формулой
$$ a times b = || a || || b || sin(theta) $$
Геометрически — это площадь параллелограмма, сформированного из исходных векторов a и b.
Приведем пример.
|
a = [1, 2, 3] b = [4, 5, 6] np.cross(a, b) |
Подведем итог
Сегодня мы ввели понятие вектора, познакомились с базовыми операциями с векторами, в частности, изучили скалярное произведение векторов и научились находить скалярную и векторную проекцию одного вектора на другой.
Перейдем к рассмотрению векторного пространства.