4.1 Скалярное произведение, его свойства и вычисление
Опр.1Скалярным
произведением
векторов называется число, равное
произведению модулей этих векторов на
косинус угла между ними.
Обозначается
скалярное произведение
или
или
=
(4.1)
1
OC=,OD=
.
Если
учесть, что в формуле (4.1) произведение
равно проекции вектора
на ось вектора
,
получим:
.
Аналогично
– есть проекция
на ось вектора
,
т.е.
.
Учитывая сказанное,
получим 2-е определение скалярного
произведения.
Опр.2
Скалярное
произведение векторов равно произведению
модуля
одного из них на проекцию на него же
второго
вектора.
(4.2)
(определение
скалярного произведения через проекции).
Формула
(4.1) так же как и (4.2) часто используется
при решении задач
Механический смысл скалярного произведения
В
механике часто приходится вычислять
работу, совершаемую переменной силой,
если точка её приложения перемещается
по прямой.
Если
сила f
перемещается по вектору
(от начала к концу), то работа, производимая
этой силой, равна скалярному произведению
силыf
на вектор
:
.
(4.3)
Свойства скалярного
произведения
Относительно
скалярного произведения имеют место
следующие законы:
10 (коммутативный
или переместительный закон);
20 (ассоциативный или
сочетательный
закон);
30 (дистрибутивный
или
распределительный
закон);
40 ;
50 ,
еслии обратно: если
Скалярное
произведение в координатах
Если
два вектора заданы в координатах
и
,
то скалярное произведение их равно
сумме произведений одноимённых координат:
.
(4.4)
Необходимым
и достаточным условием перпендикулярности
двух векторов является равенство:
.
(4.5)
Угол между векторами
вычисляется по формуле:
.
(4.6)
71
4.2
Векторное произведение векторов
Опр.
3 Векторным
произведением
векторов
и
называется
вектор
,
который удовлетворяет трём условиям:
1.Он
перпендикулярен к перемножаемым векторам
;
2.Длина
его (модуль) равна произведению модулей
перемножаемых векторов на синус угла
между ними:
;
(4.7)
Направлен
он таким образом, что если посмотреть
из его конца, то кратчайший поворот
первого перемножаемого вектора ко
второму должен быть виден против хода
часовой стрелки.
2
Обозначается
векторное произведение:
или
.
Геометрический смысл векторного произведения
Из определения векторного произведения
видно, что модуль его численно равен
площади параллелограмма, построенного
на этих векторах, как на составляющих,
т.е.
(рисунок 2).
Так
как
, то
.
(4.8)
Механический смысл векторного произведения
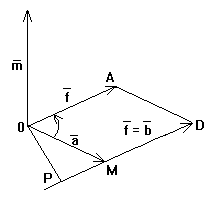
19
Пусть
заданы две точки О и М. Пусть сила
приложена к т. М и равна вектору
,
а из точки О в т. М идёт вектор,
(т.е.).
Тогда
моментом силы f
относительно точки
называется векторное произведение
векторови
,
т.е. вектор,
равный:
,
(4.9)
так
как
(рисунок 19).
Вектор
(момент
силы)
перпендикулярен к векторами
,
имеет длину, равную площади параллелограмма,
построенного на векторахи
.
Если
из точки
опустить перпендикуляр на вектор
,
то—
есть плечо силы,
т.е. модуль момента равен произведению
модуля силына плечо
(рисунок
19),
где
OP
— высота параллелограмма
,
—
длина основания.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
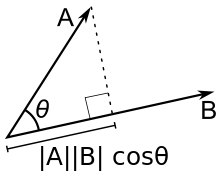
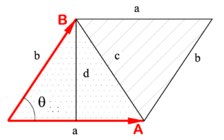
Помимо очевидных сложения, вычитания и умножения на константу, у векторов можно ввести и свои особенные операции, которые нам упростят жизнь.
#Скалярное произведение
Скалярное произведение (англ. dot product) двух векторов равно произведению их длин и косинуса угла между ними. Для него справедлива следующая формула:
$$
a cdot b = |a| cdot |b| cdot cos theta = x_a x_b + y_a y_b
$$
Она доказывается муторно и чисто технически, так что мы это делать не будем.
Геометрически, она равна проекции вектора $b$ на вектор $a$, помноженный на длину $а$:
Полезные свойства:
- Скалярное произведение симметрично ($a cdot b = b cdot a$).
- Перпендикулярные вектора должны иметь нулевое скалярное произведение.
- Если угол острый, то скалярное произведение положительное.
- Если угол тупой, то скалярное произведение отрицательное.
Добавим в нашу реализацию отдельный оператор для него:
int operator*(r a, r b) { return a.x * b.x + a.y * b.y; }
#Векторное произведение
Векторное произведение (англ. cross product, также называется косым или псевдоскалярным) для двух векторов равно произведению их длин и синуса угла между ними — причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:
$$
a times b = |a| cdot |b| cdot sin theta = x_a y_b — y_a x_b
$$
Так же, как и со скалярным произведением, доказательство координатной формулы оставляется упражнением читателю. Если кто-то захочет это сделать: это следует из линейности обоих произведений (что в свою очередь тоже нужно доказать) и разложения по базисным векторам $overline{(0, 1)}$ и $overline{(1, 0)}$.
Геометрически, это ориентированная площадь параллелограмма, натянутого на вектора $a$ и $b$:
Его свойства:
- Векторное произведение антисимметрично: $a times b = — (b times a)$.
- Коллинеарные вектора имеют нулевое векторное произведение.
- Если $b$ «слева» от $a$, то векторное произведение положительное.
- Если $b$ «справа» от $a$, то векторное произведение отрицательное.
Для него обычно тоже перегружают оператор — либо ^, либо %:
int operator^(r a, r b) { return a.x*b.y - b.x*a.y; }
Примечание. Вообще говоря, формально векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но пока в нашем двумерном мире об этом думать не надо.
Скалярное и векторное произведения тесно связаны с углами между векторами и могут использоваться для подсчета величин вроде ориентированных углов и площадей, которые обычно используются для разных проверок.
Когда они уже реализованы, использовать произведения гораздо проще, чем опираться на алгебру. Например, можно легко вычислить угол между двумя векторами, подставив в знакомый нам atan2 векторное и скалярное произведение:
double angle(r a, r b) {
return atan2(a ^ b, a * b);
}
В дальнейшем, свойства произведений помогут нам в определении взаимного расположения точек и, например, прямой, поэтому важно эти свойства понять и крепко запомнить.
Скалярное произведение
Скалярное произведение — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.
$$ c = |overline a||overline b|cos(theta )$$
Обычно для скалярного произведения векторов $overline a$ и $overline b$ используется одно из следующих обозначений:
$$ c= (overline a,overline b) = overline acdotoverline b$$
Скалярным произведением двух векторов $overline a$ и $overline b$ будет скалярная величина, равная сумме попарного произведения координат векторов $overline a$ и $overline b$.
Для плоскости:
Скалярное произведение векторов $overline a = (a_x, a_y)$ и $overline b = (b_x, b_y)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y $$
Для пространства:
Скалярное произведение двух векторов в пространстве $overline a = (a_x, a_y, a_z)$ и $overline b = (b_x, b_y, b_z)$ можно найти воспользовавшись следующей формулой:
$$ overline acdotoverline b = a_x b_x + a_y b_y + a_z b_z $$
Векторное произведение
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Определение:
Векторным произведением вектора $overline a$ на вектор $overline b$ в трёхмерном евклидовом пространстве называется вектор $overline c$, удовлетворяющий следующим требованиям:
- длина вектора $overline c$ равна произведению длин векторов $overline a$ и $overline c$ на синус угла между ними (т. е. площади параллелограмма, образованного векторами $overline a$ и $overline b$
$$ | overline c| = | overline a| cdot | overline b|cdot sin (theta ),$$ - вектор $overline c$ ортогонален каждому из векторов $overline a$ и $overline b$;
- вектор $overline c$ направлен так, что тройка векторов $(overline a,overline b,overline c)$ является правой.
Понятие правой и левой тройки векторов:
Совместим начала векторов в одной точке. Упорядоченная тройка некомпланарных векторов $(overline a,overline b,overline c)$ в трёхмерном пространстве называется правой, если с конца вектора $overline c$ кратчайший поворот от вектора $overline a$ к вектору $overline b$ виден наблюдателю против часовой стрелки. И наоборот, если кратчайший поворот виден по часовой стрелке, то тройка называется левой.
Название правой и левой тройки пошло от определения направления тройки с помощью руки человека:
Правая тройка. Указательный палец к среднему пальцу двигается против часовой стрелки.
Векторное произведение обозначают:
$$overline c = overline a times overline b = [overline a, overline b]$$
Получение координат вектора $overline c$:
Если два вектора $overline a$ и $overline {b}$ представлены в правом ортонормированном базисе координатами $ overline a=(a_x,a_y,a_z), overline b=(b_x,b_y,b_z)$, то их векторное произведение имеет координаты:
$$ overline a timesoverline b = (a_yb_z — a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x).$$
Для запоминания этой формулы удобно использовать мнемонический определитель:
$$overline a timesoverline b = begin{vmatrix}
i & j & k \
a_x & a_y & a_z \
b_x & b_y & b_z \
end{vmatrix}, $$
где $i=(1,0,0), j=(0,1,0), k=(0,0,1)$.
Псевдоскалярное произведение двух векторов
Псевдоскалярным (или косым) произведением векторов $overline{a}$ и $overline{b}$ на плоскости называют число
$$c = | overline a| cdot | overline b|cdot sin (theta ),$$
где $theta$ — угол вращения (против часовой стрелки) от $overline{a}$ к $overline{b}$. Приставка «псевдо» означает, что объект может менять или не менять знак при отражениях пространства.
Псевдоскалярное произведение обозначают так:
$$c = overline a wedge overline b.$$
Если хотя бы один из векторов нулевой, то полагают $overline a wedge overline b = 0$.
Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
С его помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.
Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является смешанное произведение.
Основные свойства:
- Линейность: $overline a wedge (lambda overline b + muoverline c ) = lambdaoverline awedgeoverline b + muoverline a wedge overline c$. Где $lambda, mu$ — произвольные вещественные числа.
- Антикоммутативность: $overline a wedgeoverline b = -overline bwedgeoverline a$.
- Ориентированная площадь треугольника ABC выражается формулой $S = (overline{AB}wedgeoverline{AC}) / 2$, а его площадь равна модулю этой величины.
- $overline a wedge overline b = 0$ — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости.
- Пусть заданы вектора $overline a = (a_1, a_2), overline b = (b_1, b_2)$. Тогда их псевдоскалярное произведение равно $overline a wedgeoverline b = a_1b_2 — a_2b_1$.
Использование в геометрических задачах
Пример 1. Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому достаточно посчитать косое произведение векторов $overline{P_1P_2}$ и $overline{P_1M}$ и по его знаку сделать вывод.
Пример 2. Определить, принадлежит ли точка отрезку.
Пусть точки $P_1(x_1, y_1), P_2(x_2, y_2)$ — концы заданного отрезка. Необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через $P_1, P_2$. Далее нужно определить лежит ли точка между точками $P_1$ и $P_2$. Для этого используем скалярное произведение векторов $overline{MP_1}, overline{MP_2}$. Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. $overline{P_1P_2} wedge overline{P_1M} = 0$ – косое произведение (точка лежит на прямой);
2. $(overline{MP_1}, overline{MP_2}) ≤ 0$ – скалярное произведение (точка лежит между $P_1$ и $P_2$).
Пример 3. Определить, пересекаются ли две прямые (прямые не совпадают).
Если прямые заданы точками $P_1(x_1, y_1), P_2(x_2, y_2), M_1(x_3, y_3), M_2(x_4, y_4)$, то условие их параллельности заключается в проверки косого произведения векторов $overline{P_1P_2}$ и $overline{M_1M_2}$: если оно равно нулю, то прямые параллельны, иначе — пересекаются.
Пример 4. Определить, пересекаются ли два отрезка.
Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Необходимо проверить, лежат ли концы каждого из отрезков по разные стороны относительного концов другого отрезка. Применим косое произведение векторов. Посмотрим на первый рисунок: $overline{P_1P_2}wedge overline{P_1M_2} * overline{P_1P_2}wedge overline{P_1M_1} < 0$ и $overline{M_1M_2}wedge overline{M_1P_1} * overline{M_1M_2}wedge overline{M_1P_2} < 0$. Важно обратить внимание на строгое неравенство, потому что возможен случай, при котором произведение равно нулю, но отрезки не пересекаются (отрезки лежат на одной прямой, но не имеют общих точек). Поэтому необходимо проверить, принадлежит ли хотя бы один конец каждого отрезка другому.
Еще примеры:
- https://foxford.ru/wiki/informatika/primenenie-skalyarnogo-i-vektornogo-proizvedeniya
- https://habr.com/en/post/147691/
Что такое произведение векторов
Определение
Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.
Основные типы перемножения векторов
В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Скалярное
Определение
Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.
Записывается скалярное произведение двумя способами: ( (overline a,;overline b) ) или ( overline acdotoverline b.)
Алгебраические свойства скалярного произведения
- Перестановочность. Произведение не меняется от перемены мест множителей: (overline acdotoverline b=overline bcdotoverline a.)
- Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: ((lambdaoverline a)cdotoverline b=lambda(overline acdotoverline b)(lambdaoverline a)cdot(muoverline b)=(lambdamu)(overline acdotoverline b).)
- Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: ((overline a+overline b)cdotoverline c=overline acdotoverline c+overline bcdotoverline c.)
Примечание
Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами.
Геометрические свойства скалярного умножения
- Скалярное произведение вектора на него же равняется квадрату его модуля: (overline acdotoverline a=overline a^2=overline{left|aright|}cdotoverline{left|aright|}cdotcosleft(0right)=left|overline a^2right|.)
- Если угол между векторами острый (меньше (90^circ)), то скалярное произведение этих векторов больше нуля.
- Если угол между векторами тупой (больше (90^circ)), то их скалярное произведение меньше нуля.
- Если вектора перпендикулярны (угол равен (90^circ)), то их скалярное произведение будет равняться нулю.
- Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат:( overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z.)
Геометрический смысл
Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.
(overline acdotoverline b=left|overline aright|cdot пр_overline aoverline b=overline{left|bright|}cdot пр_overline boverline a)
(пр_overline boverline a=frac{overline acdotoverline b}{left|overline bright|})
Физический смысл
Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора (overline s) под действием силы (overline F), приложенной под некоторым углом (varphi.)
Рисунок 1. Физический смысл скалярного произведения
Силу (overline F) необходимо разложить на ортогональные компоненты (overline{F_1}) и (overline{F_2}.) Тогда (overline{F_1}) будет являться проекцией силы (overline F) на вектор (overline s:)
(left|overline{F_1}right|=left|overline Fright|cdotcosleft(varphiright).)
В свою очередь, работа A вычисляется по формуле:
(A=left|overline{F_1}right|cdotleft|overline Sright|.)
Соединив данные формулы получим:
(A=left|overline Fright|cdotleft|overline Sright|cdotcosleft(varphiright),)
что является скалярным произведением векторов (overline F) и (overline s:)
(A=overline Fcdotoverline S.)
Векторное
Определение
Векторным произведением векторов overline a и overline b называют перпендикулярный им вектор overline c из правой тройки, модуль которого равняется произведению модулей векторов overline a и overline b на синус угла между ними.
Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.
Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Векторное произведение может выражаться в записи двумя способами: (overline atimesoverline b) и (lbrackoverline a,overline brbrack.)
Алгебраические свойства
- Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: (overline atimesoverline b=-(overline btimesoverline a))
- Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: ((lambdaoverline a)timesoverline b=overline atimes(lambdaoverline b)=lambda(overline atimesoverline b).)
- Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: ((overline a+overline b)timesoverline c=overline atimesoverline c+overline btimesoverline c.)
Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.
Геометрические свойства
- Если вектора (overline a) и (overline b) параллельны, то их векторное произведение равняется нулю.
- Векторное произведение векторов с известными координатами выражается в матричном виде: (overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right).)
Геометрический смысл
Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.
Рисунок 2. Геометрический смысл векторного произведения
Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:
(left|overline cright|=left|overline aright|cdotleft|overline bright|cdotsinleft(varphiright))
Площадь параллелограмма вычисляется так:
(S=left|overline aright|cdot h, где h=left|overline bright|cdotsinleft(varphiright).)
Таким образом, получаем:
(S=left|overline aright|cdotleft|overline bright|cdotsinleft(varphiright)=left|overline atimesoverline bright|)
Отсюда следует формула для площади треугольника:
(S_bigtriangleup=frac12left|overline atimesoverline bright|)
Физический смысл
В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:
(overline M=overline{AB}timesoverline F)
Смешанное умножение векторов
Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.
Свойства смешанного умножения
- ((overline atimesoverline b)cdotoverline c=overline acdot(overline btimesoverline c)=overline acdotoverline bcdotoverline c.)
- Если (overline acdotoverline bcdotoverline c) больше нуля, тройка векторов — правая.
- Если( overline acdotoverline bcdotoverline c) меньше нуля, тройка векторов — левая.
- Если вектора (overline a, overline b) и (overline c) компланарны, то их смешанное произведение равняется нулю.
Геометрический смысл
Если вектора overline a, overline b и overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.
(V_{пар.}=overline acdotoverline bcdotoverline c)
Следствием этого является формула нахождения объема пирамиды:
(V_{пир.}=frac16left(overline acdotoverline bcdotoverline cright))
Произведение векторов, примеры и решения
Задача №1
Даны вектора (overline a=(-1,;0,;3) и overline b=(2,;-3,;1).)
Найти их скалярное произведение.
Решение
Возьмем формулу скалярного произведения для векторов с известными координатами:
(overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z) и подставим имеющиеся значения:
(overline acdotoverline b=(-1)cdot2+0cdot(-3)+3cdot1=1)
Задача №2
Найти площадь треугольника с известными координатами угловых точек
Координаты точек: (A(-1,;2,;3), B(0,;-2,;1), C(1,;2,;1))
Решение
Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:
(S_bigtriangleup=frac12left|overline atimesoverline bright|)
В данном случае треугольник построен на векторах( overline{AB}) и (overline{AC}). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:
(overline{AB}=(0-(-1),;(-2)-2,;1-3)=(1,;-4,;-2))
(overline{AC}=(1-(-1),;2-2,;1-3)=(2,;0,;-2))
Векторное произведение векторов с известными координатами выполняется в матричном виде:
(overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right))
Подставляем значения векторов( overline{AB}) и (overline{AC}) в матрицу и производим вычисления:
(overline{AB}timesoverline{AC}=begin{vmatrix}i&j&k\1&-4&-2\2&0&-2end{vmatrix}=left(ibegin{vmatrix}-4&-2\0&-2end{vmatrix};;-jbegin{vmatrix}1&-2\2&-2end{vmatrix};;kbegin{vmatrix}1&-4\2&0end{vmatrix}right)=8i-2j+8k)
Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:
(S_bigtriangleup=frac12left|overline{AB}timesoverline{AC}right|=frac12sqrt{8^2+{(-2)}^2+8^2}=sqrt{132}=11.49)
-
Скалярное произведение.
Начать изучение
-
Ориентация прямой, плоскости и пространства.
Начать изучение
-
Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда.
Начать изучение
-
Смешанное произведение.
Начать изучение
-
Выражение векторного и смешанного произведения через компоненты сомножителей.
Начать изучение
-
Детерминанты второго и третьего порядков.
Начать изучение
-
Условия коллинеарности и компланарности.
Начать изучение
-
Площадь параллелограмма.
Начать изучение
-
Двойное векторное произведение.
Начать изучение
-
Биортогональный базис.
Начать изучение
-
О векторных величинах.
Начать изучение
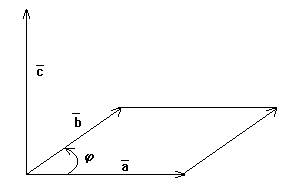
Скалярное произведение.
Под углом между векторами мы понимаем угол между векторами, равными данным и имеющими общее начало. В некоторых случаях мы будем указывать, от какого вектора и в каком направлении угол отсчитывается. Если такого указания не сделано, углом между векторами считается тот из углов, который не превосходит (pi). Если угол прямой, то векторы называются ортогональными.
Определение.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой, то угол не определен, и скалярное произведение по определению равно нулю.
Скалярное произведение векторов (boldsymbol{a}) и (boldsymbol{b}) обозначается ((boldsymbol{a}), (boldsymbol{b})) или (boldsymbol{ab}). Таким образом, мы можем написать
$$
(boldsymbol{a}, boldsymbol{b}) = |boldsymbol{a}||boldsymbol{b}| cos varphi,nonumber
$$
где (varphi) — угол между векторами (boldsymbol{a}) и (boldsymbol{b}).
Необходимо подчеркнуть следующее принципиальное обстоятельство: скалярное произведение может быть определено только после того, как будет выбрана определенная единица измерения длин векторов. Иначе приведенное выше определение не имеет смысла.
Скалярное умножение имеет следующие очевидные свойства.
- Коммутативность: для любых (boldsymbol{a}) и (boldsymbol{b}) выполнено ((boldsymbol{a, b}) = boldsymbol{b,a})).
- ((boldsymbol{a, a}) = |boldsymbol{a}|^{2}) для любого вектора (boldsymbol{a}).
- Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен 0.
- Векторы ортонормированного базиса удовлетворяют равенствам
$$
begin{array}{c}
(boldsymbol{e_{1}}, boldsymbol{e_{1}}) = (boldsymbol{e_{2}}, boldsymbol{e_{2}}) = (boldsymbol{e_{3}}, boldsymbol{e_{3}}) = 1,\
(boldsymbol{e_{1}}, boldsymbol{e_{2}}) = (boldsymbol{e_{2}}, boldsymbol{e_{3}}) = (boldsymbol{e_{3}}, boldsymbol{e_{1}}) = 0.
end{array}nonumber
$$
Утверждение 1.
Если базисные векторы попарно ортогональны, то компоненты любого вектора (boldsymbol{a}) находятся по формулам
$$
alpha_{1} = frac{(boldsymbol{a}, boldsymbol{e_{1}})}{|boldsymbol{e_{1}}|^{2}}, alpha_{2} = frac{(boldsymbol{a}, boldsymbol{e_{2}})}{|boldsymbol{e_{2}}|^{2}}, alpha_{3} = frac{(boldsymbol{a}, boldsymbol{e_{3}})}{|boldsymbol{e_{3}}|^{2}}.nonumber
$$
В частности, если базис ортонормированный
$$
alpha_{1} = (boldsymbol{a}, boldsymbol{e_{1}}), alpha_{2} = (boldsymbol{a}, boldsymbol{e_{2}}), alpha_{3} = (boldsymbol{a}, boldsymbol{e_{3}})label{ref1}
$$
и
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e_{1}})boldsymbol{e_{1}} + (boldsymbol{a}, boldsymbol{e_{2}})boldsymbol{e_{2}} + (boldsymbol{a}, boldsymbol{e_{3}})boldsymbol{e_{3}}.nonumber
$$
Доказательство.
Пусть (boldsymbol{a} = boldsymbol{a_{1}} + boldsymbol{a_{2}} + boldsymbol{a_{3}}), причем каждое слагаемое коллинеарно соответствующему базисному вектору. Мы знаем из доказанного ранее утверждения, что (alpha_{1} = pm |boldsymbol{a_{1}}|/|boldsymbol{e_{1}}|), где выбирается знак + или — в зависимости от того, одинаково или противоположно направлены (boldsymbol{a_{1}}) и (boldsymbol{e_{1}}). Но, как видно из рис. 4.1, (pm |boldsymbol{a_{1}}| = |boldsymbol{a}|cos varphi_{1}), где (varphi_{1}) — угол между векторами (boldsymbol{a}) и (boldsymbol{e_{1}}). Итак, (alpha_{1} = |boldsymbol{a}|cos varphi_{1}/|boldsymbol{e_{1}}| = (boldsymbol{a}, boldsymbol{e_{1}})/|boldsymbol{e_{1}}|^{2}).
Аналогично вычисляются и остальные компоненты.
Определение.
Косинусы углов между вектором (boldsymbol{a}) и базисными векторами декартовой прямоугольной системы координат называются направляющими косинусами этого вектора.
Направляющие косинусы — это компоненты вектора (boldsymbol{a}^{0} = boldsymbol{a}/|boldsymbol{a}|). Их отличительная особенность состоит в том, что сумма их квадратов равна квадрату длины (boldsymbol{a}^{0}), то есть 1 (см. ниже формулу eqref{ref3}).
Утверждение 2.
Для любых векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) и любых чисел (alpha) и (beta) выполнено равенство
$$
(alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c}) = alpha(boldsymbol{a}, boldsymbol{c}) + beta(boldsymbol{b}, boldsymbol{c}).nonumber
$$
В частности, ((alphaboldsymbol{a}, boldsymbol{c}) = alpha(boldsymbol{a}, boldsymbol{c})) и ((boldsymbol{a} + boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{c}) + (boldsymbol{b}, boldsymbol{c})).
Доказательство.
Если (boldsymbol{c} = 0), то утверждение очевидно. Пусть (boldsymbol{c} neq 0). Примем (boldsymbol{c}) за первый вектор базиса, а остальные выберем ортогонально к нему и между собой. Число ((alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}) — первая компонента вектора (alphaboldsymbol{a} + betaboldsymbol{b}). Точно так же ((boldsymbol{a}, boldsymbol{c})/|boldsymbol{c}|^{2}) и ((boldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}) — первые компоненты векторов (boldsymbol{a}) и (boldsymbol{b}). Согласно уже доказанному утверждению
$$
(alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2} = alpha(boldsymbol{a}, boldsymbol{c})/|boldsymbol{c}|^{2} + beta(boldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}.nonumber
$$
Отсюда прямо получается доказываемое равенство.
Легко показать, что такая же формула справедлива и для линейной комбинации любого числа векторов. Используя коммутативность скалярного умножения, мы получаем тождество
$$
(boldsymbol{a}, betaboldsymbol{b} + gammaboldsymbol{c}) = beta(boldsymbol{a}, boldsymbol{b}) + gamma(boldsymbol{a}, boldsymbol{c}).nonumber
$$
Теорема 1.
Если базис ортонормированный, то скалярное произведение векторов (boldsymbol{a}) и (boldsymbol{b}) выражается через их компоненты ((alpha_{1}), (alpha_{2}), (alpha_{3})) и ((beta_{1}), (beta_{2}), (beta_{3})) по формуле
$$
(boldsymbol{a}, boldsymbol{b}) = alpha_{1}beta_{1} + alpha_{2}beta_{2} + alpha_{3}beta_{3}label{ref2}
$$
Доказательство.
Действительно, подставим вместо (boldsymbol{a}) его разложение и воспользуемся утверждением 2:
$$
(boldsymbol{a}, boldsymbol{b}) = (alpha_{1}boldsymbol{e_{1}} + alpha_{2}boldsymbol{e_{2}} + alpha_{3}boldsymbol{e_{3}}) = alpha_{1}(boldsymbol{e_{1}}, boldsymbol{b}) + alpha_{2}(boldsymbol{e_{2}}, boldsymbol{b}) + alpha_{3}(boldsymbol{e_{3}}, boldsymbol{b}).nonumber
$$
Теперь доказываемое следует из формулы eqref{ref1}.
Отметим, что требование ортонормированности базиса очень существенно. В произвольном базисе выражение скалярного произведения через компоненты гораздо сложнее. Поэтому в задачах, связанных со скалярным произведением, чаще всего используются ортонормированные базисы.
Если почему-либо все же надо вычислить скалярное произведение в неортонормированном базисе, следует перемножить разложения сомножителей по базису и, раскрыв скобки, подставить в полученное выражение известные скалярные произведения базисных векторов.
Теорема 1 позволяет выписать выражение длины вектора через его компоненты в ортонормированном базисе
$$
|boldsymbol{a}| = sqrt{alpha_{1}^{2} + alpha_{2}^{2} + alpha_{3}^{2}}label{ref3}
$$
а также выражение косинуса угла между векторами
$$
cos varphi = frac{(boldsymbol{a}, boldsymbol{b})}{|boldsymbol{a}||boldsymbol{b}|} = frac{alpha_{1}beta_{1} + alpha_{2}beta_{2} + alpha_{3}beta_{3}}{sqrt{alpha_{1}^{2} + alpha_{2}^{2} + alpha_{3}^{2}}sqrt{beta_{1}^{2} + beta_{2}^{2} + beta_{3}^{2}}}label{ref4}
$$
Используя формулу eqref{ref3}, мы можем вычислить расстояние между точками, если заданы их координаты в декартовой прямоугольной системе координат. В самом деле, пусть точки (A) и (B) имеют координаты ((x, y, z)) и ((x_{1}, y_{1}, z_{1})). Тогда расстояние между ними равно
$$
|overrightarrow{AB}| = sqrt{(x_{1}-x)^{2} + (y_{1}-y)^{2} + (z_{1}-z)^{2}}label{ref5}
$$
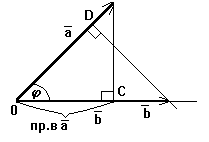
Скалярное умножение тесно связано с понятием проекции вектора. Слово “проекция” употребляется в двух смыслах. Введем соответствующие определения.
Пусть задан вектор (overrightarrow{AB}) и некоторая прямая (l). Опустим из точек (A) и (B) перпендикуляры на прямую и обозначим их основания (A’) и (B’) (рис. 4.2). Вектор (overrightarrow{A’B’}) называется (ортогональной) векторной проекцией вектора (overrightarrow{AB}) на прямую (l) и обозначается Пр(_{l}overrightarrow{AB}).
Из определения сразу следует, что векторные проекции равных векторов на параллельные прямые равны между собой.
Пусть (boldsymbol{e}) — ненулевой вектор на прямой (l). Тогда (overrightarrow{A’B’} = alphaboldsymbol{e}) при некотором (alpha). Представим (overrightarrow{AB}) в виде (overrightarrow{AB} = overrightarrow{A’B″} = alphaboldsymbol{e} + boldsymbol{b}) и заметим, что вектор (boldsymbol{b} = overrightarrow{B’B″}) ортогонален (boldsymbol{e}). Поэтому после скалярного умножения на (boldsymbol{e}) получаем ((overrightarrow{AB}, boldsymbol{e}) = alpha(boldsymbol{e}, boldsymbol{e})). Находя отсюда (alpha), имеем
$$
mbox{Пр}_{l}overrightarrow{AB} = frac{(overrightarrow{AB}, boldsymbol{e})}{|boldsymbol{e}|^{2}}boldsymbol{e}.label{ref6}
$$
Хотя на вид это выражение зависит от (boldsymbol{e}), фактически оно не меняется при замене (boldsymbol{e}) любым ненулевым вектором (lambdaboldsymbol{e}), коллинеарным (boldsymbol{e}).
Проекцию (overrightarrow{A’B’}) можно представить в виде
$$
frac{(overrightarrow{AB}, boldsymbol{e})}{|boldsymbol{e}|} frac{boldsymbol{e}}{|boldsymbol{e}|}nonumber
$$
и заметить, что ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) — это компонента (overrightarrow{A’B’}) по вектору (boldsymbol{e}^{0} = boldsymbol{e}/|boldsymbol{e}|). Так как (|boldsymbol{e}^{0}| = 1), компонента по абсолютной величине равна длине (overrightarrow{A’B’}). Она положительна, если направление (overrightarrow{A’B’}) совпадает с направлением (boldsymbol{e}), и отрицательна в противоположном случае.
Величина ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) не меняется при замене (boldsymbol{e}) на сонаправленный вектор (lambdaboldsymbol{e}), (lambda > 0), и меняет знак при замене (boldsymbol{e}) на противоположно направленный вектор.
Прямая линия называется направленной прямой (употребляются также термины ориентированная прямая и ось), если на ней указано определенное направление. Подробнее это определение рассматривается в начале следующего раздела.
Определение.
Число ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) называется скалярной проекцией вектора (overrightarrow{AB}) на ось (l), определяемую вектором (boldsymbol{e}) (или на вектор (boldsymbol{e})), и обозначается Пр(_{l}overrightarrow{AB}) или Пр(_{boldsymbol{e}}overrightarrow{AB}).
Из определения следует, что Пр(_{l}overrightarrow{AB} = |overrightarrow{AB}| cos varphi), где (varphi) — угол между (overrightarrow{AB}) и (boldsymbol{e}). Компоненты вектора в ортонормированном базисе равны его скалярным проекциям на оси координат.
Ориентация прямой, плоскости и пространства.
Выше мы дали определение ориентированной прямой (оси). Скажем о нем подробнее, с тем чтобы аналогично ввести определение ориентированной плоскости и ориентированного пространства.
Все базисы (ненулевые векторы) на прямой разделяются на два класса: векторы из одного класса направлены одинаково, а векторы из разных классов направлены противоположно. Говорится, что прямая ориентирована или что на ней задана ориентация, если из двух классов базисов выбран один. Базисы выбранного класса называются положительно ориентированными или положительными.
Задать ориентацию можно, указав какой-либо базис и считая положительно ориентированными все базисы того же класса. Однако то, что прямая ориентирована, не означает, что на ней выбран какой-то определенный базис.
Два базиса на плоскости называются одинаково ориентированными, если в обоих базисах кратчайший поворот от первого вектора ко второму производится в одну сторону, и противоположно ориентированными в противном случае. Например, на рисунке ниже, базисы в левой части ориентированы одинаково, а на правой части — противоположно. Если фиксировать какой-то базис, то любой другой ориентирован с ним либо одинаково, либо противоположно, и, таким образом, все базисы распадаются на два класса: любые два базиса одного класса ориентированы одинаково, базисы разных классов ориентированы противоположно.
Определение.
Плоскость ориентирована, если из двух классов базисов на ней выбран один класс.
Ориентацию можно задать, выбрав базис и считая положительно ориентированными все базисы одного с ним класса. Но, конечно, задание ориентации не предполагает выбор определенного базиса.
В планиметрии часто ориентируют плоскость, считая положительными те базисы, у которых кратчайший поворот от первого вектора ко второму производится против часовой стрелки. Для плоскости в пространстве это соглашение не имеет смысла, так как видимое направление поворота зависит от того, с какой стороны смотреть на плоскость. Но если выбрать одно из полупространств, ограничиваемых плоскостью, и смотреть на повороты именно из него, то класс базиса определяется видимым направлением поворота.
Определение.
Базис в пространстве называется правым, если (считая векторы имеющими общее начало) с конца третьего вектора мы видим кратчайший поворот от первого вектора ко второму направленным против часовой стрелки. В противном случае базис называется левым (рис. 4.3).
Представим себе, что на рис. 4.4 концы векторов лежат в плоскости рисунка, а их общее начало — за плоскостью. Тогда поворот от вектора (boldsymbol{e}_{1}) к вектору (boldsymbol{e}_{2}) и затем к (boldsymbol{e}_{3}) для правого базиса нам виден против часовой стрелки, а для левого — по часовой стрелке.
Определение.
Пространство называется ориентированным, если из двух классов базисов (правых или левых) выбран один. Базисы этого класса называются положительно ориентированными.
Далее мы всегда будем выбирать правую ориентацию пространства, считая положительными правые базисы. Но важно помнить, что выбор ориентации мог бы быть противоположным.
Если пространство ориентировано, то ориентацию любой плоскости в нем можно задать, указав ориентацию прямой, перпендикулярной этой плоскости. При этом положительным базисом (boldsymbol{a}), (boldsymbol{b}) на плоскости считается такой, который вместе с положительным базисом (boldsymbol{n}) на прямой составляет положительный базис пространства (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{n}). Это — внешний способ задания ориентации. Говорится, что ориентация плоскости определяется нормальным вектором (boldsymbol{n}).
Аналогично, в ориентированном пространстве можно внешним образом задать ориентацию прямой линии. Для этого нужно задать ориентацию плоскости, перпендикулярной этой прямой. Положительным базисом на прямой будет такой базис, который вместе с положительным базисом плоскости составляет положительный базис пространства.
Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда.
Если прямая ориентирована, то длине ненулевого вектора на ней можно приписать знак: считать длину положительной, если вектор ориентирован положительно, и отрицательной в противоположном случае. Именно так мы приписываем знак длине векторной проекции, когда определяем скалярную проекцию. Обобщим это определение.
Рассмотрим параллелограмм, построенный на двух векторах так, что две его смежные стороны являются векторами с общим началом. Параллелограмм называется ориентированным, если пара векторов, на которой он построен, упорядочена. На ориентированной плоскости параллелограмм считается положительно или отрицательно ориентированным, смотря по тому, как ориентирована определяющая его пара векторов.
На ориентированной плоскости принято считать площадь ориентированного параллелограмма числом со знаком: она равна площади параллелограмма (положительна), если параллелограмм ориентирован положительно, и равна той же площади со знаком минус, если отрицательно. Мы будем обозначать площадь ориентированного параллелограмма, построенного на векторах (boldsymbol{a}) и (boldsymbol{b}), через (S_{pm}(boldsymbol{a}, boldsymbol{b})).
Рассмотрим теперь параллелепипед, построенный на трех векторах так, что три его ребра, исходящие из одной вершины, являются векторами с общим началом. Параллелепипед называется ориентированным, если эти три ребра упорядочены. В ориентированном пространстве ориентация параллелепипеда положительна или отрицательна смотря по тому, какую тройку образуют векторы, на которых он построен.
В ориентированном пространстве объем ориентированного параллелепипеда — число со знаком: объем положительно ориентированного параллелепипеда считается положительным, а отрицательно ориентированного — отрицательным.
При выбранной нами правой ориентации пространства положительными считаются объемы ориентированных параллелепипедов, построенных на правых тройках векторов.
Смешанное произведение.
Если пространство ориентировано, мы можем ввести следующее определение.
Определение.
Смешанным произведением векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) (в данном порядке) называется число, равное объему ориентированного параллелепипеда, построенного на этих векторах, если они не компланарны, и равное нулю, если компланарны.
Смешанное произведение векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) обозначается ((boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c})).
При перестановке сомножителей в смешанном произведении, самое большее, может измениться только ориентация тройки векторов. Поэтому абсолютная величина смешанного произведения не зависит от порядка сомножителей. Для любых векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) мы получаем, сравнивая ориентации троек векторов (см. рис. 14),
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{c}, boldsymbol{a}, boldsymbol{b}) = (boldsymbol{b}, boldsymbol{c}, boldsymbol{a}) = -(boldsymbol{b}, boldsymbol{a}, boldsymbol{c}) = -(boldsymbol{c}, boldsymbol{b}, boldsymbol{a}) = -(boldsymbol{a}, boldsymbol{c}, boldsymbol{b}).label{ref7}
$$
Следующее предложение устанавливает связь между скалярным произведением и смешанным произведением.
Утверждение 3.
Каковы бы ни были векторы (boldsymbol{b}) и (boldsymbol{c}), найдется единственный (не зависящий от (boldsymbol{a})) вектор (boldsymbol{d}) такой, что при любом (boldsymbol{a}) выполнено равенство
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d}).label{ref8}
$$
Доказательство.
Докажем сначала существование вектора (boldsymbol{d}), а потом установим, что такой вектор возможен только один. Пусть векторы (boldsymbol{b}) и (boldsymbol{c}) коллинеарны. Тогда при любом (boldsymbol{a}) векторы (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) компланарны и ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = 0). Поэтому мы можем положить (boldsymbol{d} = 0). Рассмотрим неколлинеарные векторы (boldsymbol{b}) и (boldsymbol{c}) и предположим сначала, что (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) не компланарны. Построим на них ориентированный параллелепипед и примем за его основание параллелограмм, построенный на (boldsymbol{b}) и (boldsymbol{c}) (рис. 4.5). Введем ориентацию на прямой (OH), перпендикулярной основанию. Мы зададим ее с помощью вектора (boldsymbol{n}) длины 1, составляющего с (boldsymbol{b}) и (boldsymbol{c}) правую тройку (boldsymbol{n}), (boldsymbol{b}), (boldsymbol{c}). (Тройка (boldsymbol{b}), (boldsymbol{c}), (boldsymbol{n}) также правая.)
((boldsymbol{a}), (boldsymbol{n})) — скалярная проекция вектора (boldsymbol{a}) на (boldsymbol{n}). По модулю она равна высоте параллелепипеда (OH), а знак ее определяется ориентацией тройки (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}). Действительно, ((boldsymbol{a}, boldsymbol{n}) > 0) тогда и только тогда, когда концы векторов (boldsymbol{a}) и (boldsymbol{n}) лежат в одном полупространстве, то есть тройка (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}) правая так же, как (boldsymbol{n}), (boldsymbol{b}), (boldsymbol{c}). Таким образом, ((boldsymbol{a}), (boldsymbol{n})) положительно для правой тройки (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}) и отрицательно для левой.
Пусть положительное число (S) — площадь основания параллелепипеда. Тогда произведение ((boldsymbol{a}, boldsymbol{n})S) по модулю равно объему параллелепипеда, а знак его совпадает со знаком ((boldsymbol{a}), (boldsymbol{n})). Это значит, что ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = S(boldsymbol{a}, boldsymbol{n})). Полученное равенство совпадает с eqref{ref8}, если
$$
boldsymbol{d} = Sboldsymbol{n}.label{ref9}
$$
Осталось рассмотреть случай, когда (boldsymbol{b}) и (boldsymbol{c}) не коллинеарны, а (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) компланарны. В этом случае (boldsymbol{a}) лежит в плоскости векторов (boldsymbol{b}) и (boldsymbol{c}) и, следовательно, ортогонален вектору (boldsymbol{d}), вычисленному по формуле eqref{ref9}. Поскольку ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = 0) и ((boldsymbol{a}, boldsymbol{n}) = 0), вектор eqref{ref9} удовлетворяет равенству eqref{ref8} и в этом случае. Итак, мы нашли вектор, который удовлетворяет eqref{ref8} при любом (boldsymbol{a}) и определяется только по (boldsymbol{b}) и (boldsymbol{c}).
Допустим, что для фиксированных (boldsymbol{b}) и (boldsymbol{c}) нашлось два вектора (boldsymbol{d_{1}}) и (boldsymbol{d_{2}}) таких, что для любого а выполнено ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d_{1}})) и ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d_{2}})). Отсюда следует, что ((boldsymbol{a}, boldsymbol{d_{1}}) = (boldsymbol{a}, boldsymbol{d_{2}})) или (boldsymbol{a}(boldsymbol{d_{1}}-boldsymbol{d_{2}}) = 0). Поэтому вектор (boldsymbol{d_{1}}-boldsymbol{d_{2}}) ортогонален каждому вектору пространства и, следовательно, равен нулевому вектору. Это доказывает, что вектор (boldsymbol{d}), определяемый формулой eqref{ref8}, может быть только один. Утверждение полностью доказано.
Опишем еще раз, как вектор (boldsymbol{d}) определяется по (boldsymbol{b}) и (boldsymbol{c}).
- Если (boldsymbol{b}) и (boldsymbol{c}) коллинеарны, то (boldsymbol{d} = 0).
- Если (boldsymbol{b}) и (boldsymbol{c}) не коллинеарны, то:
- (|boldsymbol{d}| = S = |boldsymbol{b}||boldsymbol{c}|sin varphi), где (varphi) — угол между (boldsymbol{b}) и (boldsymbol{c});
- вектор (boldsymbol{d}) ортогонален векторам (boldsymbol{b}) и (boldsymbol{c});
- тройка векторов (boldsymbol{b}), (boldsymbol{c}), (boldsymbol{d}) имеет положительную ориентацию.
При нашем выборе ориентации пространства — это правая тройка.
Определение.
Вектор (boldsymbol{d}), определенный перечисленными выше условиями, или, что то же, формулой eqref{ref8}, называется векторным произведением векторов (boldsymbol{b}) и (boldsymbol{c}).
Подчеркнем, что векторное произведение, как и смешанное, определено только для ориентированного пространства. Разумеется, необходим также выбор единицы измерения длин.
Векторное произведение векторов (boldsymbol{b}) и (boldsymbol{c}) обозначают ([boldsymbol{b}, boldsymbol{c}]) или (boldsymbol{b} times boldsymbol{c}). Используя это обозначение, мы можем записать формулу eqref{ref8} в виде
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, [boldsymbol{b}, boldsymbol{c}])label{ref10}
$$
Благодаря этому равенству смешанное произведение и получило свое название.
Пример 1.
Пусть (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}) — правый ортонормированный базис. Тогда при выбранной нами правой ориентации пространства
$$
[boldsymbol{e_{2}}, boldsymbol{e_{3}}] = boldsymbol{e_{1}}, [boldsymbol{e_{3}}, boldsymbol{e_{1}}] = boldsymbol{e_{2}}, [boldsymbol{e_{1}}, boldsymbol{e_{2}}] = boldsymbol{e_{3}}.label{ref11}
$$
Если (boldsymbol{f_{1}}), (boldsymbol{f_{2}}), (boldsymbol{f_{3}}) — левый ортонормированный базис, то
$$
[boldsymbol{f_{2}}, boldsymbol{f_{3}}] = -boldsymbol{f_{1}}, [boldsymbol{f_{3}}, boldsymbol{f_{1}}] = -boldsymbol{f_{2}}, [boldsymbol{f_{1}}, boldsymbol{f_{2}}] = -boldsymbol{f_{3}}.nonumber
$$
Утверждение 4.
Векторное умножение антикоммутативно, то есть для любых векторов ([boldsymbol{b}, boldsymbol{c}] = -[boldsymbol{c}, boldsymbol{b}]).
Доказательство.
Действительно, если ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d})), то
$$
(boldsymbol{a}, boldsymbol{c}, boldsymbol{b}) = -(boldsymbol{a}, boldsymbol{d}) = (boldsymbol{a}, (-boldsymbol{d})).nonumber
$$
Получим теперь свойство линейности смешанного и векторного произведений по каждому из сомножителей. Применяя предложение 2 к скалярному произведению ((lambdaboldsymbol{a}_{1} + muboldsymbol{a}_{2}, [boldsymbol{b}, boldsymbol{c}])), мы получим
$$
(lambdaboldsymbol{a}_{1} + muboldsymbol{a}_{2}, boldsymbol{b}, boldsymbol{c}) = lambda (boldsymbol{a}_{1}, boldsymbol{b}, boldsymbol{c}) + mu(boldsymbol{a}_{2}, boldsymbol{b}, boldsymbol{c}).label{ref12}
$$
Из равенств eqref{ref7} следуют аналогичные тождества для остальных сомножителей. Например, для второго сомножителя
$$
(boldsymbol{a}, lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}) = lambda (boldsymbol{a}, boldsymbol{b}_{1}, boldsymbol{c}) + mu(boldsymbol{a}, boldsymbol{b}_{2}, boldsymbol{c}).label{ref13}
$$
Действительно, мы можем переставить интересующий нас сомножитель на первое место, раскрыть скобки, а затем выполнить обратную перестановку.
Утверждение 5.
Для любых векторов (boldsymbol{b}_{1}), (boldsymbol{b}_{2}) и (boldsymbol{c}) и любых чисел (lambda) и (mu) имеет место равенство
$$
[lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}] = lambda[boldsymbol{b}_{1}, boldsymbol{c}] + mu[boldsymbol{b}_{2}, boldsymbol{c}].nonumber
$$
Доказательство.
В самом деле, правой части формулы eqref{ref13} можно придать вид
$$
(boldsymbol{a}, lambda[boldsymbol{b}_{1}, boldsymbol{c}]) + (boldsymbol{a}, mu[boldsymbol{b}_{2}, boldsymbol{c}]).nonumber
$$
Поэтому по утверждению 2 получаем
$$
(boldsymbol{a}, [lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}]) = (boldsymbol{a}, lambda[boldsymbol{b}_{1}, boldsymbol{c}]) + mu[boldsymbol{b}_{2}, boldsymbol{c}]).nonumber
$$
Так как это верно для любого вектора (boldsymbol{a}), мы можем, выбрав ортонормированный базис (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}), подставить на место (boldsymbol{a}) последовательно каждый вектор этого базиса. В силу предложения 1 мы получим равенство всех компонент векторов ([lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}]) и (lambda[boldsymbol{b}_{1}, boldsymbol{c}] + mu[boldsymbol{b}_{2}, boldsymbol{c}]), а отсюда и равенство векторов, которое нам нужно было доказать.
Линейность векторного произведения по второму сомножителю можно получить из свойства антикоммутативности.
Выражение векторного и смешанного произведения через компоненты сомножителей.
Если заданы разложения векторов (boldsymbol{a}) и (boldsymbol{b}) по векторам некоторого базиса (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}), то мы можем раскрыть скобки:
$$
[boldsymbol{a}, boldsymbol{b}] = [(alpha_{1}boldsymbol{e}_{1} + alpha_{2}boldsymbol{e}_{2} + alpha_{3}boldsymbol{e}_{3}), (beta_{1}boldsymbol{e}_{1} + beta_{2}boldsymbol{e}_{2} + beta_{3}boldsymbol{e}_{3})] =\= (alpha_{1}beta_{2}-alpha_{2}beta_{1})[boldsymbol{e}_{1}, boldsymbol{e}_{2}] + (alpha_{2}beta_{3}-alpha_{3}beta_{2})[boldsymbol{e}_{2}, boldsymbol{e}_{3}] +\+(alpha_{3}beta_{1}-alpha_{1}beta_{3})[boldsymbol{e}_{3}, boldsymbol{e}_{1}].label{ref14}
$$
Здесь использовалась антикоммутативность векторного умножения и то, что векторное произведение двух одинаковых сомножителей — нулевой вектор. В примере 1 были сосчитаны попарные векторные произведения векторов ортонормированного базиса. Поэтому из формулы eqref{ref14} следует следующая теорема.
Теорема 2.
В положительно ориентированном ортонормированном базисе векторное произведение выражается через компоненты сомножителей формулой
$$
[boldsymbol{a}, boldsymbol{b}] = (alpha_{2}beta_{3}-alpha_{3}beta_{2})boldsymbol{e}_{1} + (alpha_{3}beta_{1}-alpha_{1}beta_{3})boldsymbol{e}_{2} + (alpha_{1}beta_{2}-alpha_{2}beta_{1})boldsymbol{e}_{3}.label{ref15}
$$
Если базис ориентирован отрицательно, перед правой частью этой формулы следует поставить знак минус.
Избежать постоянной заботы об ориентации базисов можно двумя способами. Можно договориться при правой ориентации пространства, если не оговорено противное, использовать только правые базисы. Такого соглашения мы и будем придерживаться.
Второй способ состоит в том, чтобы не фиксировать заранее ориентацию пространства, а выбирать ее так, чтобы используемый базис был ориентирован положительно. При таком подходе векторное произведение всегда вычисляется по формуле eqref{ref15}, но приходится следить за тем, как векторное произведение направлено. Этот подход принят, например, в литературе по физике.
Теорема 3.
Смешанное произведение векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) выражается через их компоненты ((alpha_{1}, alpha_{2}, alpha_{3})), ((beta_{1}, beta_{2}, beta_{3})) и ((gamma_{1}, gamma_{2}, gamma_{3})) в произвольном базисе (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}) по формуле ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (alpha_{1}beta_{2}gamma_{3} + alpha_{2}beta_{3}gamma_{1} + alpha_{3}beta_{1}gamma_{2}-alpha_{3}beta_{2}gamma_{1}-alpha_{2}beta_{1}gamma_{3}-alpha_{1}beta_{3}gamma_{2}))((boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}})).
Доказательство.
Для доказательства заметим, что ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{c}, [boldsymbol{a}, boldsymbol{b}])) и умножим скалярно обе части равенства eqref{ref14} на вектор (boldsymbol{c} = gamma_{1}boldsymbol{e_{1}} + gamma_{2}boldsymbol{e_{2}} + gamma_{3}boldsymbol{e_{3}}). Мы получим
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = gamma_{1}(alpha_{2}beta_{3}-alpha_{3}beta_{2})(boldsymbol{e_{1}}[boldsymbol{e_{2}}, boldsymbol{e_{3}}]) +\+ gamma_{2}(alpha_{3}beta_{1}-alpha_{1}beta_{3})(boldsymbol{e_{2}}[boldsymbol{e_{3}}, boldsymbol{e_{1}}]) + gamma_{3}(alpha_{1}beta_{2}-alpha_{2}beta_{1})(boldsymbol{e_{3}}[boldsymbol{e_{1}}, boldsymbol{e_{2}}]).nonumber
$$
(Слагаемые, содержащие смешанные произведения с одинаковыми сомножителями, мы не выписываем, так как они равны нулю.) Отсюда, учитывая равенства eqref{ref7} и приводя подобные члены, получаем нужный нам результат.
Детерминанты второго и третьего порядков.
Найденные нами формулы достаточно громоздки. Для их более компактной записи употребляются детерминанты (или определители) второго и третьего порядков.
Рассмотрим четыре числа (alpha_{1}), (alpha_{2}), (beta_{1}), (beta_{2}). Из них можно составить таблицу, называемую матрицей второго порядка:
$$
begin{Vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{Vmatrix}.nonumber
$$
Определение.
Число (alpha_{1}beta_{2}-alpha_{2}beta_{1}), называется детерминантом этой матрицы или детерминантом второго порядка и обозначается
$$
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}.nonumber
$$
Теперь выражение векторного произведения в правом ортонормированном базисе перепишется так:
$$
[boldsymbol{a}, boldsymbol{b}] =
begin{vmatrix}
alpha_{2}& alpha_{3}\
beta_{2}& beta_{3}
end{vmatrix}
boldsymbol{e_{1}} +
begin{vmatrix}
alpha_{3}& alpha_{1}\
beta_{3}& beta_{1}
end{vmatrix}
boldsymbol{e_{2}} +
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
boldsymbol{e_{3}}.nonumber
$$
Из компонент трех векторов можно составить таблицу — матрицу третьего порядка
$$
begin{Vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{Vmatrix}.nonumber
$$
Число
$$
alpha_{1}
begin{vmatrix}
beta_{2}& beta_{3}\
gamma_{2}& gamma_{3}
end{vmatrix}
+ alpha_{2}
begin{vmatrix}
beta_{3}& beta_{1}\
gamma_{3}& gamma_{1}
end{vmatrix}
+ alpha_{3}
begin{vmatrix}
beta_{1}& beta_{2}\
gamma_{1}& gamma_{2}
end{vmatrix},
$$
или, что то же самое,
$$
alpha_{1}
begin{vmatrix}
beta_{2}& beta_{3}\
gamma_{2}& gamma_{3}
end{vmatrix}
— alpha_{2}
begin{vmatrix}
beta_{1}& beta_{3}\
gamma_{1}& gamma_{3}
end{vmatrix}
+ alpha_{3}
begin{vmatrix}
beta_{1}& beta_{2}\
gamma_{1}& gamma_{2}
end{vmatrix},nonumber
$$
называется детерминантом этой матрицы или детерминантом третьего порядка и обозначается
$$
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}.nonumber
$$
По теореме 3 в новых обозначениях
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}
(boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}).label{ref16}
$$
В частности, в правом ортонормированном базисе
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}.label{ref17}
$$
При помощи теоремы 2 и определения детерминанта можно получить следующее выражение векторного произведения через компоненты сомножителей в правом ортонормированном базисе:
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
boldsymbol{e_{1}}& boldsymbol{e_{2}}& boldsymbol{e_{3}}\
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}
end{vmatrix}.label{ref18}
$$
Детерминанты тесно связаны с системами линейных уравнений, решения которых удобно записывать с их помощью. Дадим этому геометрическую иллюстрацию.
Пусть дана система из трех уравнений
$$
left{
begin{array}{l}
a_{1}x + b_{1}y + c_{1}z = d_{1},\
a_{2}x + b_{2}y + c_{2}z = d_{2},\
a_{3}x + b_{3}y + c_{3}z = d_{3}.
end{array}
right.nonumber
$$
Выберем в пространстве некоторый базис и рассмотрим векторы (boldsymbol{a}(a_{1}, a_{2}, a_{3})), (boldsymbol{b}(b_{1}, b_{2}, b_{3})), (boldsymbol{c}(c_{1}, c_{2}, c_{3})) и (boldsymbol{d}(d_{1}, d_{2}, d_{3})). Тогда система является координатной записью векторного равенства
$$
xboldsymbol{a} + yboldsymbol{b} + zboldsymbol{c} = boldsymbol{d}.label{ref19}
$$
Поэтому решение системы (x,y,z) — коэффициенты разложения (boldsymbol{d}) по (boldsymbol{a}, boldsymbol{b}) и (boldsymbol{c}). Мы можем быть уверены, что система имеет единственное решение, если (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) не компланарны, то есть ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) neq 0). Предположим, что это условие выполнено, и найдем решение. Для этого умножим обе части равенства eqref{ref19} скалярно на векторное произведение ([boldsymbol{b}, boldsymbol{c}]). Мы получим (x(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{d}, boldsymbol{b}, boldsymbol{c})), и, следовательно, (x) равен отношению детерминантов
$$
begin{vmatrix}
d_{1}& d_{2}& d_{3}\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}
mbox{и}
begin{vmatrix}
a_{1}& a_{2}& a_{3}\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}.nonumber
$$
Аналогично находятся и остальные неизвестные.
Остановимся на следующих свойствах детерминантов. Из равенств eqref{ref7} следует, что детерминант меняет знак при перестановке каких-либо двух строк матрицы. Формула eqref{ref12} означает, что
$$
begin{vmatrix}
lambda a_{1}’ + mu a_{1}″& lambda a_{2}’ + mu a_{2}″& lambda a_{3}’ + mu a_{3}″\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix} =\= lambda
begin{vmatrix}
a_{1}’& a_{2}’& a_{3}’\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}
+ mu
begin{vmatrix}
a_{1}″& a_{2}″& a_{3}″\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}.nonumber
$$
Условия коллинеарности и компланарности.
Утверждение 6.
Каков бы ни был базис ((boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}})), попарные векторные произведения базисных векторов линейно независимы.
Доказательство.
Докажем это от противного. Рассмотрим равенство
$$
lambda[boldsymbol{e_{2}}, boldsymbol{e_{3}}] + mu[boldsymbol{e_{3}}, boldsymbol{e_{1}}] + nu[boldsymbol{e_{1}}, boldsymbol{e_{2}}] = 0nonumber
$$
и допустим, что какой-нибудь коэффициент, пусть для определенности (lambda), отличен от нуля. Умножив обе части равенства скалярно на (boldsymbol{e_{1}}), мы получим (lambda(boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}) = 0). Полученное противоречие доказывает наше предложение.
Следующие предложения дают условия на компоненты векторов в произвольном базисе, необходимые и достаточные для компланарности или коллинеарности векторов.
Утверждение 7.
Равенство нулю детерминанта матрицы из компонент трех векторов необходимо и достаточно для компланарности векторов.
Доказательство.
Это сразу следует из формулы eqref{ref16}, поскольку ((boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}) neq 0).
Утверждение 8.
Пусть ((alpha_{1}, alpha_{2}, alpha_{3})) и ((beta_{1}, beta_{2}, beta_{3})) — компоненты векторов (boldsymbol{a}) и (boldsymbol{b}) в некотором базисе. Векторы (boldsymbol{a}) и (boldsymbol{b}) коллинеарны тогда и только тогда, когда
$$
begin{vmatrix}
alpha_{2}& alpha_{3}\
beta_{2}& beta_{3}
end{vmatrix}
=
begin{vmatrix}
alpha_{3}& alpha_{1}\
beta_{3}& beta_{1}
end{vmatrix}
=
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
= 0.label{ref20}
$$
Доказательство.
Достаточность условия очевидна: из равенств eqref{ref20} по формуле eqref{ref14} следует обращение в нуль ([boldsymbol{a}, boldsymbol{b}]), что равносильно коллинеарности векторов. Заметим, что мы пользуемся формулой eqref{ref14}, которая справедлива для произвольного базиса. Наоборот, из обращения в нуль ([boldsymbol{a}, boldsymbol{b}]) и формулы eqref{ref14} мы можем вывести eqref{ref20}, так как в силу предложения 6 векторы ([boldsymbol{e_{2}}, boldsymbol{e_{3}}]), ([boldsymbol{e_{3}}, boldsymbol{e_{1}}]) и ([boldsymbol{e_{1}}, boldsymbol{e_{2}}]) линейно независимы.
Утверждение 9.
Обращение в нуль детерминанта матрицы из компонент двух векторов на плоскости необходимо и достаточно для коллинеарности этих векторов.
Доказательство.
Для доказательства будем считать, что плоскость помещена в пространство и базис в этой плоскости дополнен третьим вектором до базиса в пространстве. Тогда векторы (boldsymbol{a}(alpha_{1}, alpha_{2})) и (boldsymbol{b}(beta_{1}, beta_{2})) на плоскости имеют компоненты ((alpha_{1}, alpha_{2}, 0)) и ((beta_{1}, beta_{2}, 0)) относительно базиса в пространстве. Применяя предложение 8, получаем условие
$$
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
= 0.nonumber
$$
Остальные два детерминанта равны нулю, так как (alpha_{3} = beta_{3} = 0).
Площадь параллелограмма.
Если в пространстве заданы два неколлинеарных вектора, имеющих общее начало, то площадь параллелограмма, построенного на этих векторах, может быть найдена через их компоненты в ортонормированном базисе по формуле
$$
S = |[boldsymbol{a}, boldsymbol{b}]| = sqrt{(alpha_{2}beta_{3}-alpha_{3}beta_{2})^{2} + (alpha_{3}beta_{1}-alpha_{1}beta_{3})^{2} + (alpha_{1}beta_{2}-alpha_{2}beta_{1})^{2}}.label{ref21}
$$
Еще одно выражение для площади параллелограмма мы получим, если заметим, что
$$
|[boldsymbol{a}, boldsymbol{b}]|^{2} = |boldsymbol{a}|^{2}|boldsymbol{b}|^{2} sin^{2} varphi = |boldsymbol{a}|^{2}|boldsymbol{b}|^{2} (1-cos varphi).nonumber
$$
В результате
$$
S^{2} =
begin{vmatrix}
|boldsymbol{a}|^{2}& (boldsymbol{a}, boldsymbol{b})\
(boldsymbol{a}, boldsymbol{b})& |boldsymbol{b}|^{2}
end{vmatrix}.label{ref22}
$$
Найдем теперь площадь ориентированного параллелограмма на ориентированной плоскости. Можно считать, что ориентация плоскости определена вектором (boldsymbol{n}), перпендикулярным плоскости и составляющим правую тройку с положительным базисом на плоскости. Более того, будем предполагать, что (|boldsymbol{n}| = 1).
Пусть дан ориентированный параллелограмм, построенный на векторах (boldsymbol{a}) и (boldsymbol{b}). Рассмотрим скалярную проекцию Пр(_{boldsymbol{n}}[boldsymbol{a}, boldsymbol{b}]). Так как ([boldsymbol{a}, boldsymbol{b}]) и (boldsymbol{n}) коллинеарны, проекция по модулю равна (|[boldsymbol{a}, boldsymbol{b}]|), то есть площади параллелограмма. Она положительна, если ([boldsymbol{a}, boldsymbol{b}]) и (boldsymbol{n}) сонаправлены, и отрицательна в противном случае. Но вектор ([boldsymbol{a}, boldsymbol{b}]) сонаправлен с (boldsymbol{n}), если пара векторов (boldsymbol{a}), (boldsymbol{b}) на плоскости ориентирована положительно. Поэтому Пр(_{n}[boldsymbol{a}, boldsymbol{b}]) равна площади ориентированного параллелограмма, построенного на (boldsymbol{a}) и (boldsymbol{b}). По определению проекции
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) = (boldsymbol{n}, boldsymbol{a}, boldsymbol{b})nonumber
$$
(напомним, что (|boldsymbol{n}| = 1)). На плоскости выберем произвольный (не обязательно положительный) базис (boldsymbol{e_{1}}), (boldsymbol{e_{2}}). Примем (boldsymbol{n}) за третий базисный вектор и выразим смешанное произведение через координаты сомножителей:
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) =
begin{vmatrix}
0& 0& 1\
alpha_{1}& alpha_{2}& 0\
beta_{1}& beta_{2}& 0
end{vmatrix}
(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{n}).nonumber
$$
Вычисляя детерминант, находим, что он равен (alpha_{1}beta_{2}-alpha_{2}beta_{1}), и получаем окончательное выражение
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) =
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
S_{pm}(boldsymbol{e}_{1}, boldsymbol{e}_{2}).label{ref23}
$$
Эта формула сходна с формулой eqref{ref16}. По существу это та же формула, написанная для двумерного пространства. Если ((boldsymbol{e}_{1}, boldsymbol{e}_{2})) — положительный ортонормированный базис, то
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) = alpha_{1}beta_{2}-alpha_{2}beta_{1}.label{ref24}
$$
Для площади неориентированного параллелограмма в ортонормированном базисе мы получаем формулу
$$
S = |alpha_{1}beta_{2}-alpha_{2}beta_{1}|.label{ref25}
$$
которая следует и из eqref{ref21}.
Двойное векторное произведение.
Определение.
Выражение ([boldsymbol{a}, [boldsymbol{b}, boldsymbol{c}]]) называется двойным векторным произведением.
Лемма.
$$
[boldsymbol{a} [boldsymbol{b}, boldsymbol{c}]] = (boldsymbol{a}, boldsymbol{c}) boldsymbol{b}-(boldsymbol{a}, boldsymbol{b}) boldsymbol{c}.label{ref26}
$$
Доказательство.
Выберем правый ортонормированный базис ((boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})) так, чтобы (boldsymbol{e}_{1}) был коллинеарен (boldsymbol{b}), а (boldsymbol{e}_{2}) был компланарен (boldsymbol{b}) и (boldsymbol{c}). Тогда (boldsymbol{b} = beta boldsymbol{e}_{1}), (boldsymbol{c} = gamma_{1} boldsymbol{e}_{1} + gamma_{1} boldsymbol{e}_{2}) и (boldsymbol{a} = alpha_{1} boldsymbol{e}_{1} + alpha_{2} boldsymbol{e}_{2} + alpha_{3} boldsymbol{e}_{3}). Отсюда получаем ([boldsymbol{b}, boldsymbol{c}] = betagamma_{2}boldsymbol{e}_{3}) и
$$
[boldsymbol{a} [boldsymbol{b}, boldsymbol{c}]] = -alpha_{1}betagamma_{2}boldsymbol{e}_{2} + alpha_{2}betagamma_{2}boldsymbol{e}_{1}.nonumber
$$
С другой стороны,
$$
(boldsymbol{a}, boldsymbol{c}) boldsymbol{b} = (alpha_{1}gamma_{1} + alpha_{2}gamma_{2})betaboldsymbol{e}_{1}, (boldsymbol{a}, boldsymbol{b}) boldsymbol{c} = alpha_{1}beta(gamma_{1}boldsymbol{e}_{1} + gamma_{2}boldsymbol{e}_{2}).nonumber
$$
Разность правых частей двух последних равенств совпадает с найденным выше двойным векторным произведением. Это заканчивает доказательство.
Биортогональный базис.
Определение.
Базис, составленный из векторов
$$
boldsymbol{e^{*}}_{1} = frac{[boldsymbol{e}_{2}, boldsymbol{e}_{3}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}, boldsymbol{e^{*}}_{2} = frac{[boldsymbol{e}_{3}, boldsymbol{e}_{1}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}, boldsymbol{e^{*}}_{3} = frac{[boldsymbol{e}_{1}, boldsymbol{e}_{2}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}
$$
называется взаимным или биортогональным для базиса (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}).
Из утверждения 6 вытекает, что (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), не компланарны и действительно образуют базис. Название “биортогональный” связано с тем, что векторы обоих базисов, имеющие разные номера, ортогональны: ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{j}) = 0) при (i neq j). Кроме того, ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{i}) = 1) для всех (i).
Нетрудно проверить, что ортонормированный базис совпадает со своим взаимным.
Утверждение 10.
Если (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — базис, взаимный с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}), то произвольный вектор (boldsymbol{a}) раскладывается по этим базисам так:
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e^{*}}_{1}) boldsymbol{e}_{1} + (boldsymbol{a}, boldsymbol{e^{*}}_{2}) boldsymbol{e}_{2} + (boldsymbol{a}, boldsymbol{e^{*}}_{3}) boldsymbol{e}_{3},label{ref27}
$$
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e}_{1}) boldsymbol{e^{*}}_{1} + (boldsymbol{a}, boldsymbol{e}_{2}) boldsymbol{e^{*}}_{2} + (boldsymbol{a}, boldsymbol{e}_{3}) boldsymbol{e^{*}}_{3}.label{ref28}
$$
Доказательство.
Чтобы доказать eqref{ref27}, умножим равенство (boldsymbol{a} = alpha_{1}boldsymbol{e}_{1} + alpha_{2}boldsymbol{e}_{2} + alpha_{3}boldsymbol{e}_{3}) скалярно сначала на (boldsymbol{e^{*}}_{1}), затем на (boldsymbol{e^{*}}_{2}) и на (boldsymbol{e^{*}}_{3}). Мы получим (alpha_{1} = (boldsymbol{a}, boldsymbol{e^{*}}_{1})), (alpha_{2} = (boldsymbol{a}, boldsymbol{e^{*}}_{2})), (alpha_{3} = (boldsymbol{a}, boldsymbol{e}_{3})). Аналогично доказывается равенство eqref{ref28}.
Утверждение 11.
Если (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — базис, взаимный с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}), то базис (boldsymbol{e^{**}}_{1}, boldsymbol{e^{**}}_{2}, boldsymbol{e^{**}}_{3}), взаимный с (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), совпадает с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}).
Доказательство.
Действительно, равенство eqref{ref28}, написанное для базиса (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), имеет вид
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e_{1}^{*}}) boldsymbol{e_{1}^{**}} + (boldsymbol{a}, boldsymbol{e_{2}^{*}}) boldsymbol{e_{2}^{**}} + (boldsymbol{a}, boldsymbol{e_{3}^{*}}) boldsymbol{e_{3}^{**}}.nonumber
$$
Подставляя сюда вместо а последовательно ((boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})) и учитывая, что ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{j}) = 0) при (i neq j), а ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{i}) = 1), получаем (boldsymbol{e}_{1} = boldsymbol{e^{**}}_{1}), (boldsymbol{e}_{2} = boldsymbol{e^{**}}_{2}) и (boldsymbol{e}_{3} = boldsymbol{e^{**}}_{3}).
Числа ((boldsymbol{a}, boldsymbol{e}_{1})), ((boldsymbol{a}, boldsymbol{e}_{2})) и ((boldsymbol{a}, boldsymbol{e}_{3})) однозначно определяют вектор а с помощью векторов базиса (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). Они называются ковариантными координатами вектора а в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). По отношению к базису (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — это обычные координаты вектора. Обычные координаты, чтобы подчеркнуть их отличие от ковариантных координат, называют контрвариантными координатами.
О векторных величинах.
В приложениях математики часто рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил и так далее. Векторам, изображающим такие величины, приписывается размерность. Не вдаваясь в существо дела, мы ограничимся изложением формальных правил действий с размерностями.
С формальной точки зрения, размерность — это одночлен, составленный из какого-то набора символов. Такие одночлены перемножаются и делятся, как обычные одночлены. Имеют место следующие правила действий с векторными величинами:
- Модуль векторной величины имеет ту же размерность, что и сама величина.
- Складывать векторные величины можно только в том случае, когда их размерности совпадают. При этом размерность суммы та же, что и у слагаемых.
- При умножении векторной величины на скалярную их размерности перемножаются.
- Скалярное, векторное и смешанное произведения имеют размерность, равную произведению размерностей сомножителей. Это легко следует из первого правила, определений скалярного и векторного произведений и формулы eqref{ref10}.
Для того чтобы изобразить векторную величину на чертеже, мы должны условиться о масштабе: сколькими единицами длины (например, см) мы будем изображать одну единицу данной размерности (например, км, м/с, Н).
Если в векторном произведении сомножители имеют размерность длины, то произведение имеет размерность площади. Масштаб для изображения единиц площади выбирается так, чтобы одна единица площади изображалась одной линейной единицей. При этом длина векторного произведения будет численно равна площади параллелограмма, построенного на сомножителях.
Поскольку единица длины у нас выбрана и не меняется, указанное соглашение ни к каким противоречиям привести не может. Однако оно не так безобидно, как может показаться. Именно, два математика, пользующиеся этим соглашением, но разными единицами длины (например, француз, пользующийся сантиметрами, и англичанин — дюймами), для одних и тех же векторов нарисуют несовпадающие векторные произведения. Как связаны длины этих произведений, если дюйм равен примерно 2,5 см?