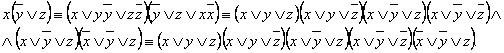Математическая логика.Примеры приведения формул к СДНФ и СКНФ
Примеры приведения формул к СДНФ и СКНФ
Пример 1. Следующую формулу привести к СДНФ, предварительно приведя ее равносильными преобразованиями к ДНФ:
$$A equiv a ( bc rightarrow ab) .$$
Решение. (A equiv a ( bc rightarrow ab) equiv a ( bar{b}bar{c} vee ab) equiv a ( bar{b} vee bar{c} vee ab) equiv)
(equiv a bar{b} vee a bar{c} vee ab equiv ДНФ A).
$$A equiv ДНФ A equiv abar{b } ( c vee bar{c}) vee abar{c} ( b vee bar{b}) vee ab ( c vee bar{c})equiv$$
$$equiv abar{b} c vee a bar{b} bar{c} vee abbar{c} vee a bar{b} bar{c} vee abc vee abbar{c} equiv$$
$$equiv abar{b} c vee a bar{b} bar{c} vee abbar{c} vee vee abc equiv СДНФ A.$$
Ответ. (СДНФ A equiv abar{b} c vee a bar{b} bar{c} vee abbar{c} vee vee abc .)
Пример 2. Для формулы из примера 1 найти СДНФ путем составления таблицы истинности.
Решение. Составим таблицу истинности для формулы (A equiv a ( bc rightarrow ab).)
| (a) | (b) | (c) |
(bc) |
(ab) |
(bcrightarrow ab) |
(A) |
| 1 | 1 | 1 |
1 |
1 |
1 |
1 |
| 1 | 1 | 0 |
0 |
1 |
1 |
1 |
| 1 | 0 | 1 |
0 |
0 |
1 |
1 |
| 1 | 0 | 0 |
0 |
0 |
1 |
1 |
| 0 | 1 | 1 |
1 |
0 |
0 |
0 |
| 0 | 1 | 0 |
0 |
0 |
1 |
0 |
| 0 | 0 | 1 |
0 |
0 |
1 |
0 |
| 0 | 0 | 0 |
0 |
0 |
1 |
0 |
Ответ. Тогда (СДНФ A equiv abc vee ab bar{c} vee abar{b}c vee abar{b}bar{c}.)
Пример 3. Для формулы из примера 1 найти СКНФ путем равносильных преобразований, предварительно приведя ее к КНФ.
Решение. Из примера 1: (A equiv abar{b} vee a bar{c} vee ab.) Далее (A equiv a ( bar{b} vee bar{c} vee b) equiv a wedge 1equiv aequiv КНФ A.)
$$A equiv КНФ A equiv a vee ( b wedge bar{b}) equiv ( a vee b) wedge ( a vee bar{b}) equiv$$
$$equiv (( a vee b) vee c wedge bar{c}) wedge (( a vee bar{b}) vee c wedge bar{c}) equiv$$
$$equiv ( a vee b vee c) wedge(a vee b vee bar{c}) wedge ( a vee bar{b} vee c) wedge ( a vee bar{b} vee bar{c}) equiv СКНФ A.$$
Ответ. (СКНФ A equiv ( a vee b vee c) wedge(a vee b vee bar{c}) wedge ( a vee bar{b} vee c) wedge ( a vee bar{b} vee bar{c}).)
Пример 4. Для формулы из примера 1 найти СКНФ, записав предварительно СДНФ ее отрицания, а потом воспользовавшись формулой двойственности.
Решение. СКНФ
$$bar{A} equiv overline{СДНФ bar{A}} equiv overline{bar{a}bc vee bar{a}bbar{c} vee bar{a}bar{b}c vee bar{a}bar{b}bar{c}} equiv$$
$$equiv ( a vee bar{b} vee bar{c} ) wedge ( a vee bar{b} vee c) wedge ( a vee b vee bar{c}) wedge ( a vee b vee c) .$$
Ответ. СКНФ (A equiv ( a vee bar{b} vee bar{c} ) wedge ( a vee bar{b} vee c) wedge ( a vee b vee bar{c}) wedge ( a vee b vee c) .)
2012-11-05 • Просмотров [ 25023 ]
-
Аналитическое построение сднф и скнф
Под аналитическим
построением будем понимать получение
формулы вида СДНФ или СКНФ с помощью
эквивалентных преобразований заданной
формулы.
Пусть функция
представлена формулой со связками
{, &, }.
Тогда для преобразования формулы в
совершенную дизъюнктивную нормальную
форму необходимо вначале представить
формулу в виде
– логической суммы логических
произведений. Этого можно добиться с
помощью законов дистрибутивности или
других тождеств. Затем добавить к каждой
элементарной конъюнкции (каждому
логическому произведению переменных)
единичные множители, составленные по
закону исключенного третьего из символов
тех переменных, которых недостает в
данной конъюнкции до полного набора
переменных, и далее выполнить
преобразования, раскрывая скобки и
приводя «подобные члены» по закону
идемпотентности.
Например, f(x,y,z)=.
Первое слагаемое в формуле преобразуем
по закону Де Моргана, во втором слагаемом
раскроем скобки с помощью закона
дистрибутивности и поменяем местами
сомножители, используя закон
коммутативности. Тогда f(x,y,z)=
– это выражение имеет требуемую форму:
логическая сумма логических произведений
переменных или их отрицаний, такая
форма называется также дизъюнктивной
нормальной формой (ДНФ). Теперь к
каждой элементарной конъюнкции в ДНФ
добавим единичный множитель: к первой
–,
ко второй –
и к третьей
.
Получим:
f(x,y,z)==
=.
Теперь приведем «подобные члены»:
.
Полученное выражение и есть СДНФ данной
функции.
Для представления
функции в виде совершенной конъюнктивной
нормальной формы необходимо вначале
представить её в виде произвольной
конъюнктивной нормальной формы
(КНФ) – это выражение вида
(логическое произведение логических
сумм переменных или их отрицаний, или
конъюнкция элементарных дизъюнкций).
Этого можно добиться с помощью приведенных
выше законов. Затем в каждую элементарную
дизъюнкцию добавить нулевые слагаемые,
составленные по закону противоречия
из недостающих ей до полного набора
переменных. Далее выполнить преобразования,
применяя законы дистрибутивности,
коммутативности и идемпотентности.
Например,
.
Приведем к виду КНФ:
f(x,y,z)=.
В этом выражении 4 элементарных
дизъюнкции, причем в первой из них не
хватает до полного набора переменных
y и z,
во второй – переменной z,
в третьей – х и в четвертой – у.
Добавим их в виде нулевых слагаемых,
пользуясь законом противоречия. Тогда
f(x,y,z)==
=
.
Теперь воспользуемся законами
идемпотентности и коммутативности и
получим СКНФ(f(x,y,z))=
=
-
Теорема о тройке связок
-
Всякая
истинностная функция может быть
выражена формулой, содержащей только
связки {, &, }.
-
Доказательство:
Рассмотрим два случая:
(1) если f(х1,х2,…,хn)0
– противоречие. Тогда очевидно,
f(х1,х2,…,хn)=,
если f(х1,х2,…,хn)1
– тавтология, то f(х1,х2,…,хn)=,
(2) если f(х1,х2,…,хn)0
(и 1).
Представим её в виде СДНФ или СКНФ.
Тогда в полученной формуле имеются
только связки из множества {, &, }.
Следствие
1: о парах связок
Для любой из следующих
пар связок {Ø,&},
{Ø,Ú}
и {Ø,®}
и для любой функции алгебры логики
можно построить формулу, реализующую
эту функцию и содержащую связки только
из заданной пары.
Доказательство:
Пусть для функции
построена совершенная дизъюнктивная
(или конъюнктивная) нормальная форма,
т.е. формула, содержащая только связки
{Ø,&,Ú}.
Заметим, что выражение
,
является тождеством. Поэтому все
выражения вида хÚу
можно заменить эквивалентными
и содержащими только связки {Ø,&}.
Тем самым, полученная в результате
проведенных преобразований формула,
содержит только связки из заданной
пары.
Для представления
функции формулой со связками {Ø,Ú}
аналогичным образом можно воспользоваться
тождеством
.
И, выполнив замены всех подформул вида
х&у на эквивалентную формулу
,
получить в результате формулу со
связками из заданной пары.
Для перехода в формуле
к последней паре связок {Ø,®}
можно воспользоваться тождествами:
и
Следствие
2: об уникальных связках
Любая истинностная
функция может быть выражена формулой
с использованием лишь одной связки
стрелки Пирса – {¯}или
штриха Шеффера – {½}.
Доказательство:
|
x |
у |
x¯у |
x½у |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
|
Таблица 16 |
СДНФ(x¯у)=
СКНФ(x½у)=
Нетрудно также
проверить, что имеют место следующие
тождества:
и
.
Тем самым,
х & y = = (x¯x) ¯ (у¯у)
и х y = = (xx) (уу).
Последние тождества можно использовать
для перехода в формуле от связок {Ø,&,Ú}
к стрелке Пирса или к штриху Шеффера.
Вообще говоря, связки
¯ и
являются единственными элементарными
функциями, каждой из которых достаточно
для записи формул всех других истинностных
функций.
Рассмотрим применение
следствий 1 и 2 на примере.
Запишем формулу ху
с использованием только связок {Ø,&}:
ху =.
С использованием связок {Ø,Ú}:
ху =.
С использованием только {¯}:
ху = ((х¯х) ¯ у) ¯ ((х¯х) ¯ у).
И, наконец, с использованием только
{}: ху = (x (уу)).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение. Совершенной дизъюнктивной формулой формулы алгебры высказываний (СДНФ) называется ДНФ, в которой:
1) различны все члены дизъюнкции;
2) различны все члены каждой конъюнкции;
3) ни одна конъюнкция не содержит одновременно переменную и отрицание этой переменной;
4) каждая конъюнкция содержит все переменные, входящие в формулу, т. е. имеет вид
,
где дизъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=1.
Теорема (о СДНФ). Для всякой не равной тождественному нулю формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СДНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки дизъюнктивных членов.
Определение. Совершенной конъюнктивной формулой формулы алгебры высказываний (СКНФ) называется КНФ, в которой:
1) различны все члены конъюнкции;
2) различны все члены каждой дизъюнкции;
3) ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной;
4) каждая дизъюнкция содержит все переменные, входящие в исходную формулу, т. е. имеет вид
,
где конъюнкция берется по всем наборам с=(с1, с2, …, сn) из 0 и 1, для которых F(c)=0.
Теорема (о СКНФ). Для всякой не равной тождественной единице формулы логики высказываний F(x1, x2, …, xn) существует такая формула F1, зависящая от того же списка переменных и находящаяся в СКНФ относительно этого списка, что F1 выражает собой формулу F. Формула F1 определена однозначно с точностью до перестановки конъюнктивных членов.
Опишем два способа приведения к совершенным нормальным формам.
1-й способ – аналитический.
Приведение к СДНФ. Алгоритм приведения:
1) привести формулу с помощью равносильных преобразований к ДНФ;
2) удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);
3) из одинаковых членов дизъюнкции (если такие окажутся) удалить все, кроме одного;
4) из одинаковых членов каждой конъюнкции (если такие окажутся) удалить все, кроме одного;
5) если в какой-нибудь конъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член и применить закон дистрибутивности конъюнкции относительно дизъюнкции;
6) если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
7) Полученная формула и является СДНФ данной формулы.
Пример 27.
Привести следующие формулы к СДНФ с помощью равносильных преобразований:
1) ;
2) ;
3) .
Решение.
1) .
2)
3)
Приведение к СКНФ. Алгоритм приведения:
1) привести формулу с помощью равносильных преобразований к КНФ;
2) удалить члены конъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);
3) из одинаковых членов конъюнкции (если такие окажутся) удалить все, кроме одного;
4) из одинаковых членов каждой дизъюнкции (если такие окажутся) удалить все, кроме одного;
5) если в какой-нибудь дизъюнкции не содержится переменной xi из числа переменных, входящих в исходную формулу, добавить к этой дизъюнкции член и применить закон дистрибутивности дизъюнкции относительно конъюнкции;
1) если в полученной конъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.
2) Полученная формула и является СКНФ данной формулы.
Пример 28.
Привести следующие формулы к СКНФ с помощью равносильных преобразований:
1) ;
2) .
Решение.
1)
2)
2-й способ – табличный.
Составляем таблицу истинности для данной функции.
Приведение к СДНФ. Алгоритм приведения.
Строим таблицу значений формулы. Рассматриваем только те строки, в которых значение формулы равно единице. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем, аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 – без отрицания. Наконец, образуем дизъюнкцию всех полученных конъюнкций.
Пример 29.
Построить СДНФ для данных формул логики высказываний.
1) .
2)
Решение.
1) .
Строим таблицу истинности (табл. 2.11) для формулы F:
Таблица 2.11 Таблица истинности для формулы из примера 29
|
N/н |
x |
y |
z |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
1 |
0 |
|
4 |
1 |
0 |
0 |
1 |
1 |
1 |
|
5 |
1 |
0 |
1 |
1 |
1 |
1 |
|
6 |
1 |
1 |
0 |
0 |
0 |
0 |
|
7 |
1 |
1 |
1 |
0 |
1 |
1 |
Рассматриваем только 4, 5 и 7 наборы, так как только на этих наборах формула принимает значение равное единице.
СДНФ имеет вид:
2)
Строим таблицу истинности (табл.
2.12) для формулы F:
Таблица 2.12 Таблица истинности для формулы из примера 29
|
N/н |
x |
y |
x® y |
F=(x® y) |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
0 |
0 |
|
3 |
1 |
1 |
1 |
1 |
СДНФ (1): № 3: F = x y.
Приведение к СКНФ. Алгоритм приведения.
Рассматриваем только те строки таблицы, где формула принимает значение 0. Каждой такой строке соответствует дизъюнкция всех переменных (без повторений). Причем аргумент, принимающий значение 0, берется без отрицания, значение 1 – с отрицанием. Наконец, образуют конъюнкцию полученных дизъюнкций.
Пример 30.
Построить СКНФ для данных формул логики высказываний.
1) .
2)
Решение.
1) Строим таблицу значений, используя предыдущий пример (табл. 2.13).
Таблица 2.13 Таблица истинности для формулы из примера 30
|
N/н |
x |
y |
z |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
0 |
|
7 |
1 |
1 |
1 |
1 |
Рассматриваем только наборы, на которых формула принимает значение ноль.
СКНФ (0): № 0, 1, 2, 3, 6:
2) Строим таблицу значений, используя предыдущий пример (табл. 2.14).
Таблица 2.14 Таблица истинности для формулы из примера 30
|
N/н |
x |
y |
F=(x® y) |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
СКНФ (0): № 0, 1, 2:
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
Определение
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
((A;wedge;overline B;wedge;C);vee;(B;wedge;C))
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
Примечание
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
Определение
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
КНФ имеет вид:
((A;vee;overline B;vee;C);wedge;(A;vee;C))
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
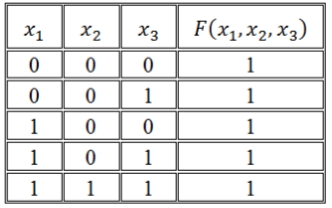
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
- Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
(F(x_1,;x_2,;x_3);=;(overline{x_1}wedgeoverline{x_2}wedgeoverline{x_3});vee(overline{x_1};wedge;overline{x_2};wedge;x_3);vee(x_1;wedge;overline{x_2};wedge;overline{x_3});vee;(x_1;wedge;overline{x_2};wedge;x_3);vee;(x_1;wedge;x_2;wedge;x_3))
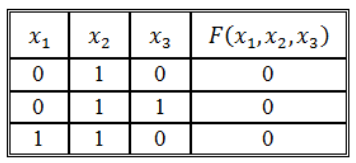
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
(F(x_1,;x_2,;x_3);=;(x_1;vee;overline{x_2};vee;x_3);wedge;(x_1;vee;overline{x_2};vee;overline{x_3});wedge;(overline{x_1};vee;overline{x_2};vee;x_3))
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: ( equiv , = , Leftrightarrow .)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
- Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
(x;vee;xy;=;x)
(x(x;vee;y);=;x;)
Доказательство эквивалентности:
(x;vee;xy;=;x;cdot;l;vee;xy;=;x(l;vee;y);=;x)
(x(x;vee;y);=;xx;vee;xy;=;x;vee;xy;=;x)
Склеивание
(xy;vee;xoverline y;=;x)
Доказательство эквивалентности:
(xy;vee;xoverline y;=;x(y;vee;overline y);=;x;cdot;l;=;x)
Обобщенное склеивание
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z)
Доказательство эквивалентности
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z;vee;xyz;vee;xyoverline z;=;xz;vee;yoverline z)
Расщепление
(x;vee;overline xy;=;x;vee;y)
Доказательство эквивалентности
(x;vee;overline xy;=;xy;vee;xoverline y;vee;overline xy;=;xy;vee;xoverline y;vee;xy;vee;overline xy;=;x;cdot;l;;vee;y;cdot;l;=;x;vee;y)
Примеры с решением
Задача №1
Приведите к СКНФ (((((Arightarrow B)rightarrowoverline A)rightarrowoverline B)rightarrowoverline C)).
Через применение закона де Моргана и правила( x;rightarrow;y;=;overline x;vee;y) упростим выражения:
(F;=;((((A;rightarrow;B);rightarrow;overline A);rightarrowoverline B);rightarrow;overline C);=;(((overline A;vee;B);rightarrow;overline A);rightarrow;overline B);rightarrowoverline C;);=)
(=;((((overline A;vee;B);rightarrowoverline A);rightarrowoverline B);rightarrow;overline C);=;((overline{((overline A;vee;B)};vee;overline A);rightarrowoverline B);rightarrowoverline C);=)
(=(((overline A;vee;B);vee;overline A);rightarrow;overline B);rightarrow;overline C);=((overline{(overline{(overline Avee B)};vee;overline A;)};vee;overline B);rightarrow;overline C);=)
(=;(overline{(overline{(overline{(overline A;vee;B)};vee;overline A)};vee;overline B)};vee;overline C);=;(((A;vee;B);vee;overline A);vee;overline B);vee;overline C;=)
(=;((overline{(overline A;vee;B)};vee;overline A);wedge;B);vee;overline C;=;(((A;wedge;overline B);vee;overline A);wedge B);vee;overline C;=)
(=((Aoverline B;vee;overline A);vee;overline A);wedge;B);vee;overline C;=(((A;wedge;overline B);vee;overline A);wedge;B);vee;overline C;=)
(=;((Aoverline B;vee;overline A);wedge;B);vee;overline C;=;(Aoverline BB;vee;overline AB);vee;overline C;=;(0;vee;overline AB);vee;overline C;=;overline AB;vee;overline C)
Далее приведем выражение к КНФ:
(F;=;overline AB;vee;overline C;;=;(overline A;vee;overline C);wedge;(B;vee;overline C))
Далее приведем выражение к СКНФ:
(F;=;(overline A;vee;overline C);wedge;(B;vee;overline C);=;(overline A;vee:overline C;vee;Boverline B);wedge;(Aoverline A;vee;B;v;overline C);=)
(=;(overline A;vee;overline C;vee;B);wedge;(A;vee;B;vee;overline C);wedge;(overline A;vee;overline C;vee;overline B);wedge;(overline A;vee;B;;overline C))
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции (f(widetilde x^n))
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2))
Преобразуем функцию:
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2) = ((overline{x_1}x_2;cdot;overline{x_3};);vee;(overline{overline{x_1}x_2};cdot;x_3));cdot;(overline{x_1x_3};vee;x_2);=)
(=;((overline{x_1}x_2overline{x_3});vee;((overline{overline{x_1}};vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=;((overline{x_1}x_{2;}overline{x_3});vee;((x_1;vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;x_1x_3;vee;overline{x_2}x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=(overline{x_1}x_2overline{x_3};cdot(x_1vee x_3vee x_2);vee;x_1x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2);vee;overline{x_2}x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2));=)
(=;(overline{x_1}x_2overline{x_3};vee;(x_1;x_3overline{x_1};vee;x_1x_3overline{x_3};vee;x_1x_3x_2);vee;(overline{x_2}x_3overline{x_1};vee;overline{x_2}x_3overline{x_3};vee;overline{x_2}x_3x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;0;vee;0;vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3;vee;0;vee;0);=)
(=;overline{x_1}x_2overline{x_3};vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3)
Диана Загировна Филиппенкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
-
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;
-
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных дизъюнкций;
-
ни одна из дизъюнкций не содержит одинаковых переменных;
-
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных конъюнкций;
-
ни одна из конъюнкций не содержит одинаковых переменных;
-
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
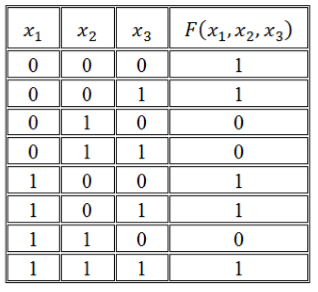
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]
Воспользуемся правилом построения СКНФ:
Рисунок 3.
Получим СКНФ:
[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]
«Построение СКНФ и СДНФ по таблице истинности» 👇
Пример 2
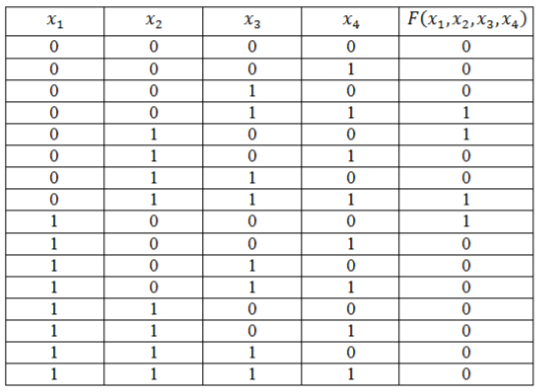
Функция задана таблицей истинности:
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
-
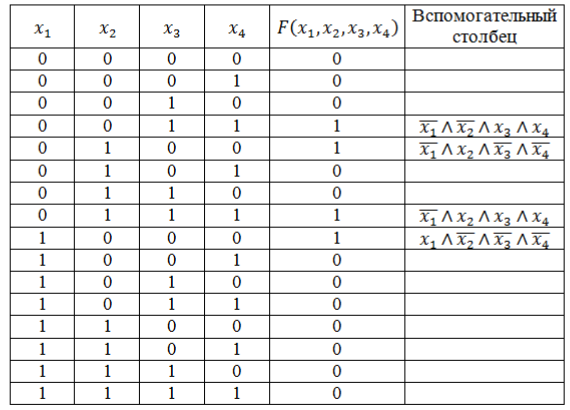
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]
-
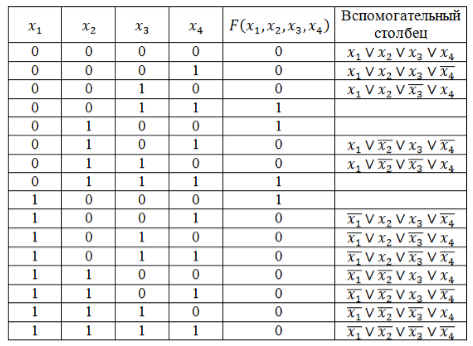
Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме