Как найти сколько точек минимума функции - Исправление недочетов и поиск решений вместе с Examum.ru

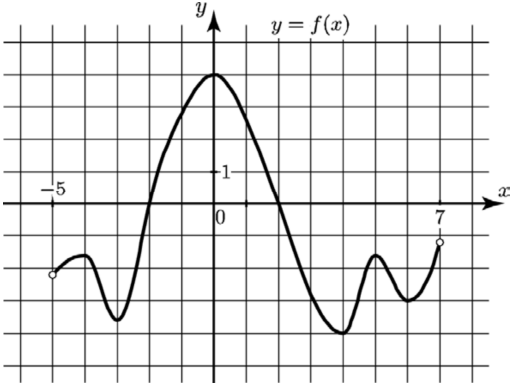
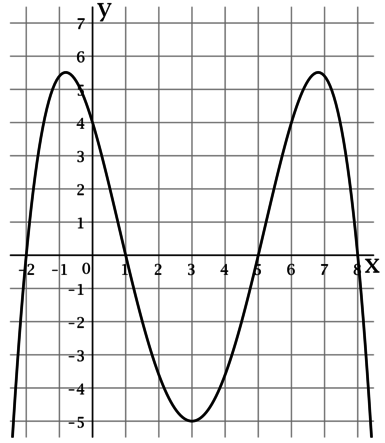
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

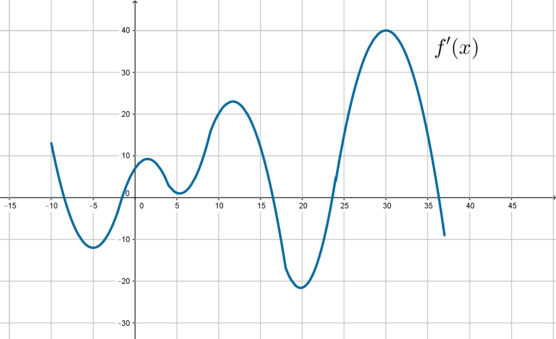
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

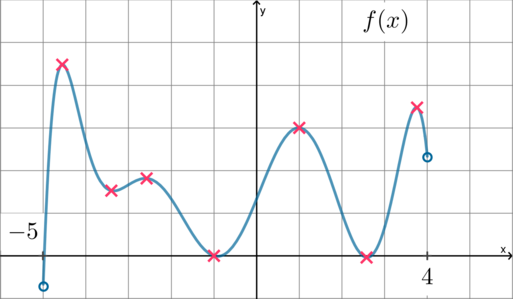
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Если в точке x * выполняется условие:

Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /₂, f(3)=3 8 /₈₁
Ответ: f_min= 5 /₂ при x=2; f_max=9 при x=1

Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π /₃+2πk, k∈Z – точки минимума функции; , значит x=- π /₃+2πk, k∈Z – точки максимума функции.

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Экстремумы функции: признаки существования, примеры решений

Экстремумы функции, их необходимый и достаточный признаки

Точка экстремума функции — это точка области определения функции, в которой значение функции принимает минимальное или максимальное значение. Значения функции в этих точках называются экстремумами (минимумом и максимумом) функции.

Нахождение эктремумов функции может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графиков. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций. И ещё потребуются таблица производных простых функций и таблица производных сложных функций (откроются в новом окне), так как в примерах указано, какая именно табличная производная найдена.

Рассмотрим график непрерывной функции (рисунок снизу).

Определение. Точка x 1 области определения функции f(x) называется точкой максимума функции, если значение функции в этой точке больше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) > f(x 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 1 максимум.

Определение. Точка x 2 области определения функции f(x) называется точкой минимума функции, если значение функции в этой точке меньше значений функции в достаточно близких к ней точках, расположенных справа и слева от неё (то есть выполняется неравенство f(x 0 ) 0 + Δx) ). В этом случае говорят, что функция имеет в точке x 2 минимум.

Допустим, точка x 1 — точка максимума функции f(x) . Тогда в интервале до x 1 функция возрастает, поэтому производная функции больше нуля ( f ‘(x) > 0 ), а в интервале после x 1 функция убывает, следовательно, и производная функции меньше нуля ( f ‘(x) ). Тогда в точке x 1 производная функции равна нулю или не существует.

Допустим также, что точка x 2 — точка минимума функции f(x) . Тогда в интервале до x 2 функция убывает, а производная функции меньше нуля ( f ‘(x) ), а в интервале после x 2 функция возрастает, а производная функции больше нуля ( f ‘(x) > 0 ). В этом случае также в точке x 2 производная функции равна нулю или не существует.

Теорема Ферма (необходимый признак существования экстремума функции). Если точка x 0 — точка экстремума функции f(x) , то в этой точке производная функции равна нулю ( f ‘(x) = 0 ) или не существует.

Определение. Точки, в которых производная функции равна нулю или не существует, называются критическими точками.

Пример 1. Рассмотрим функцию .

В точке x = 0 производная функции равна нулю, следовательно, точка x = 0 является критической точкой. Однако, как видно на графике функции, она возрастает во всей области определения, поэтому точка x = 0 не является точкой экстремума этой функции.

Таким образом, условия о том, что производная функции в точке равна нулю или не существует, являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести и другие примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Поэтому нужно располагать достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно — максимум или минимум.

Теорема (первый достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с «плюса» на «минус», то точкой максимума, а если с «минуса» на «плюс», то точкой минимума.

Если же вблизи точки x 0 , слева и справа от неё, производная сохраняет знак, то это означает, что функция либо только убывает, либо только возрастает в некоторой окрестности точки x 0 . В этом случае в точке x 0 экстремума нет.

Итак, чтобы определить точки экстремума функции, требуется выполнить следующее:

Найти производную функции.
Приравнять производную нулю и определить критические точки.
Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с «плюса» на «минус», то критическая точка является точкой максимума, а если с «минуса» на «плюс», то точкой минимума.
Вычислить значение функции в точках экстремума.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 2. Найти экстремумы функции .

Решение. Найдём производную функции (в таблице производных сложных функций — производная 6):

Приравняем производную нулю, чтобы найти критические точки:

Так как для любых значений «икса» знаменатель не равен нулю, то приравняем нулю числитель:

Получили одну критическую точку x = 3 . Определим знак производной в интервалах, разграниченных этой точкой:

в интервале от минус бесконечности до 3 — знак минус, то есть функция убывает,

в интервале от 3 до плюс бесконечности — знак плюс, то есть функция возрастает.

То есть, точка x = 3 является точкой минимума.

Найдём значение функции в точке минимума:

Таким образом, точка экстремума функции найдена: (3; 0) , причём она является точкой минимума.

Теорема (второй достаточный признак существования экстремума функции). Критическая точка x 0 является точкой экстремума функции f(x) , если вторая производная функции в этой точке не равна нулю ( f »(x) ≠ 0 ), причём, если вторая производная больше нуля ( f »(x) > 0 ), то точкой максимума, а если вторая производная меньше нуля ( f »(x) ), то точкой минимума.

Замечание 1. Если в точке x 0 обращаются в нуль и первая, и вторая производные, то в этой точке нельзя судить о наличии экстремума на основании второго достаточного признака. В этом случае нужно воспользоваться первым достаточным признаком экстремума функции.

Замечание 2. Второй достаточный признак экстремума функции неприменим и тогда, когда в стационарной точке первая производная не существует (тогда не существует и вторая производная). В этом случае также нужно вопользоваться первым достаточным признаком экстремума функции.

Локальный характер экстремумов функции

Из приведённых определений следует, что экстремум функции имеет локальный характер — это наибольшее и наименьшее значение функции по сравнению с близлежайшими значениями.

Предположим, вы рассматриваете свои заработки в отрезке времени протяжённостью в один год. Если в мае вы заработали 45 000 рублей, а в апреле 42 000 рублей и в июне 39 000 рублей, то майский заработок — максимум функции заработка по сравнению с близлежайшими значениями. Но в октябре вы заработали 71 000 рублей, в сентябре 75 000 рублей, а в ноябре 74 000 рублей, поэтому октябрьский заработок — минимум функции заработка по сравнению с близлежашими значениями. И вы легко видите, что максимум среди значений апреля-мая-июня меньше минимума сентября-октября-ноября.

Говоря обобщённо, на промежутке функция может иметь несколько экстремумов, причём может оказаться, что какой-либо минимум функции больше какого-либо максимума. Так, для функции изображённой на рисунке выше, .

То есть не следует думать, что максимум и минимум функции являются, соответственно, её наибольшим и наименьшим значениями на всём рассматриваемом отрезке. В точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума — наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.

Поэтому можно уточнить приведённое выше понятие точек экстремума функции и называть точки минимума точками локального минимума, а точки максимума — точками локального максимума.

Ищем экстремумы функции вместе

Пример 3. Найти экстремумы функции и построить её график.

Решение. Функция определена и непрерывна на всей числовой прямой. Её производная (и первое, и второе слагаемые — табличная производная 3) существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых , т.е. , откуда и . Критическими точками и разбивают всю область определения функции на три интервала монотонности: . Выберем в каждой из них по одной контрольной точке и найдём знак производной в этой точке.

Для интервала контрольной точкой может служить : находим . Взяв в интервале точку , получим , а взяв в интервале точку , имеем . Итак, в интервалах и , а в интервале . Согласно первому достаточному признаку экстремума, в точке экстремума нет (так как производная сохраняет знак в интервале ), а в точке функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдём соответствующие значения функции: , а . В интервале функция убывает, так как в этом интервале , а в интервале возрастает, так как в этом интервале .

Чтобы уточнить построение графика, найдём точки пересечения его с осями координат. При получим уравнение , корни которого и , т. е. найдены две точки (0; 0) и (4; 0) графика функции. Используя все полученные сведения, строим график (см. в начале примера).

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти экстремумы функции и построить её график.

Областью определения функции является вся числовая прямая, кроме точки , т.е. .

Для сокращения исследования можно воспользоваться тем, что данная функция чётная, так как . Поэтому её график симметричен относительно оси Oy и исследование можно выполнить только для интервала .

Находим производную (каждое слагаемое находим как табличную производную 3) и критические точки функции:

1) ;

2) ,

но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.

Таким образом, заданная функция имеет две критические точки: и . Учитывая чётность функции, проверим по второму достаточному признаку экстремума только точку . Для этого найдём вторую производную и определим её знак при : получим . Так как и , то является точкой минимума функции, при этом .

Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:

(здесь символом обозначено стремление x к нулю справа, причём x остаётся положительным; аналогично означает стремление x к нулю слева, причём x остаётся отрицательным). Таким образом, если , то . Далее, находим

т.е. если , то .

Точек пересечения с осями график функции не имеет. Рисунок — в начале примера.

Найти экстремумы функции самостоятельно, а затем посмотреть решение

Пример 5. Найти экстремумы функции .

Пример 6. Найти экстремумы функции .

Пример 7. Найти экстремумы функции .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Продолжаем искать экстремумы функции вместе

Пример 8. Найти экстремумы функции .

Решение. Найдём область определения функции. Так как должно выполняться неравенство , то из получаем .

Найдём первую производную функции (производная вида 2 в таблице производных сложной функции):

Найдём критические точки функции:

Точки и не могут быть точками экстремума, так как находятся на границе области определения функции. В точке производная функции меняет знак с плюса на минус, а в точке — с минуса на плюс. Следовательно, — точка максимума, а точка — точка минимума функции.

Найдём значения функции в этих точках:

Таким образом, экстремумы функции:

Пример 9. Найти экстремумы функции .

Решение. Найдём область определения функции.

Найдём критические точки функции:

Таким образом, у данной функции две критические точки: и . Определим значения производной в критических точках. При переходе через точку производная функции продолжает убывать (сохраняет знак минус), а при переходе через точку — начинает возрастать (меняет знак с минуса на плюс). Следовательно, — точка минимума функции.

Найдём значение функции в точке минимума:

Таким образом, минимум функции:

Пример 10. Найти экстремумы функции .

Решение. Найдём первую производную функции (первое слагаемое — производная вида 12 в таблице производных простых функций, второе — производная вида 6 в таблице производных сложной функции):

Найдём критические точки функции:

Так как для любого действительного x должно выполняться условие , то

Таким образом, данная функция имеет одну критическую точку. Определим значения производной в критической точке. При переходе через точку производная функции начинает убывать (меняет знак с плюса на минус). Следовательно, — точка максимума функции.

Найдём значение функции в точке максимума:

Таким образом, максимум функции:

источники:

http://cos-cos.ru/math/327/

http://function-x.ru/function_extremum.html

Источник

Всего: 18 1–18

Добавить в вариант

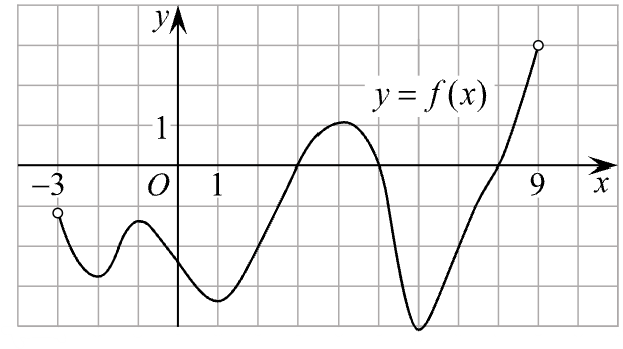
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y  =  12 или совпадает с ней.

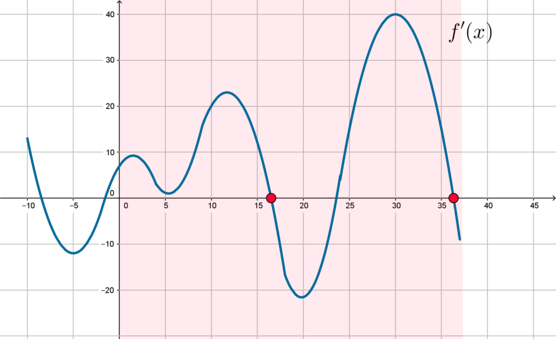
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 10). Найдите количество точек минимума функции f(x) на отрезке [−3; 8].

На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y  =  6 или совпадает с ней.

На рисунке изображен график производной функции f(x), определенной на интервале (−18; 6). Найдите количество точек минимума функции f(x) на отрезке [−13;1].

Рассматривается набор гирек, масса каждой из которых  — целое число граммов, а общая масса всех гирек равна 500 граммам. Такой набор называется правильным, если любое тело, имеющее массу, выраженную целым числом граммов от 1 до 500, может быть уравновешено некоторым количеством гирек набора и притом единственным образом (тело кладется на одну чашу весов, гирьки  — на другую; два способа уравновешивания, различающиеся лишь заменой некоторых гирек на другие той же массы, считаются одинаковыми).

а)  Является ли правильным набор, состоящий из 167 гирек массой по одному грамму, одной гирьки массой 165 граммов и одной гирьки массой 168 граммов?

б)  Приведите пример правильного набора, в котором не все гирьки по одному грамму.

в)  Сколько существует различных правильных наборов? (Два набора различны, если некоторая гирька участвует в этих наборах неодинаковое число раз.)

Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.

В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t³ часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t³ часов в неделю, они производят t приборов.

За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?

Найдите все значения а, при каждом из которых система уравнений

имеет ровно три решения.

Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел в А равно q и никакие два числа в множестве А не являются взаимно простыми. Найдите все числа множества А, если:

а)  q  =  210, произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа.

б)  q  =  390, произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа.

в)  q  =  330, произведение всех чисел из А не является четвертой степенью никакого целого числа, а сумма всех чисел из А равна 755.

Про число А известно, что оно не является 2020‐й степенью натурального числа и имеет ровно 2020 различных делителей, включая его самого и единицу.

а)  Может ли А быть кубом целого числа?

б)  Может ли А быть четвертой степенью целого числа?

в)  Найдите наименьшее значение А.

Ученик решил построить таблицу умножения всех целых неотрицательных чисел меньших некоторого натурального числа n. При этом он все время делал одну и ту же ошибку  — вместо значения произведения записывал в таблицу остаток от деления этого произведения на число n. Например, таблица для n  =  4 приведена на рисунке.

x	1	2	3
0	0	0	0
1	1	2	3
2	2	0	2
3	3	2	1

а)  Может ли на диагонали такой таблицы стоять ровно 9 нулей?

б)  Может ли общее количество нулей (не считая тех, которые находятся в первой строке или первом столбце  — шапке таблицы) в таблице быть равным 41?

в)  Найдите максимальное количество нулей в одной строке таблицы (исключая строку со всеми нулями), если n  — нечетное и 15 ≤ n ≤ 35.

Имеются три коробки: в первой  — 97 камней, во второй  — 104 камня, в третьей пусто. За один ход разрешается взять по камню из двух коробок и положить в оставшуюся.

а)  Может ли в первой коробке оказаться 97 камней, во второй  — 89, в третьей  — 15?

б)  Может ли в третьей коробке оказаться 201 камень?

в)  Известно, что в первой коробке 1 камень. Найдите наибольшее возможное количество камней в третьей коробке.

Всего: 18 1–18

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Тема 7.

Взаимосвязь функции и ее производной

Производная и точки экстремума функции

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

взаимосвязь функции и ее производной

Решаем задачи

На рисунке изображен график производной функции f(x), определенной на отрезке Найдите количество точек
максимума функции f(x) на отрезке [0;37].

Показать ответ и решение

Точка максимума — значение в котором производная меняет свой знак с «» на «» при движении слева направо.
Следовательно, в этой точке график производной пересекает ось абсцисс «сверху вниз». На отрезке [0;37] таких точек две.

На рисунке изображен график функции , определенной на интервале . Найдите
произведение точек экстремума этой функции.

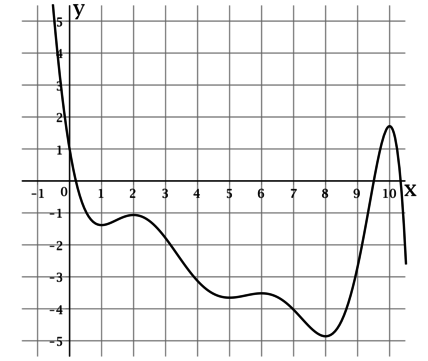
На рисунке изображен график функции , определенной на интервале . Найдите
сумму точек экстремума этой функции на отрезке [1;6] .

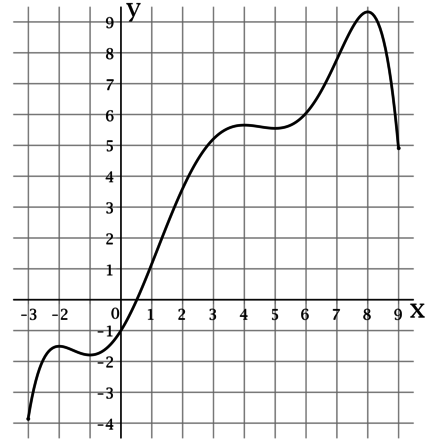
На рисунке изображен график функции определенной на интервале Найдите сумму точек экстремума этой
функции.

Показать ответ и решение

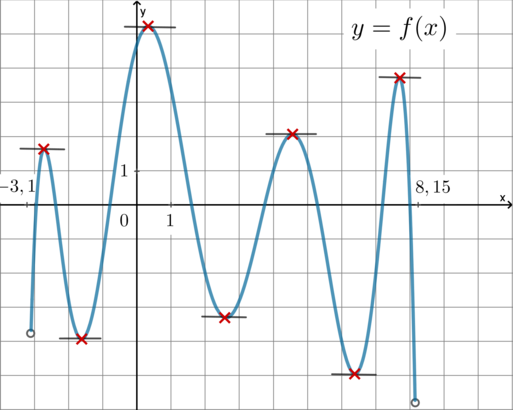
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное
значение.

По рисунку можно определить, что функция f(x) достигает локально минимальные значения в точках − 1, 2 и
5, а локально максимальные значения в точках 0, 4 и 8. Таким образом, сумма точек экстремума этой функции
равна

На рисунке изображен график функции , определенной на интервале . Найдите
сумму точек экстремума этой функции.

На рисунке изображён график производной функции f(x),
определённой на интервале Найдите количество точек максимума
функции f(x), принадлежащих отрезку

Показать ответ и решение

Точки максимума — это точки, в которых функция меняет свой характер
монотонности с возрастания на убывание, если смотреть слева направо.
Следовательно, в них производная меняет свой знак с плюса на минус.

Значит, на рисунке нужно найти те точки отрезка в которых
график функции пересекает ось Ox, причем сверху вниз. Таких точек
две.

На рисунке изображён график функции определённой на интервале
Найдите наименьшее значение функции f(x) на отрезке

Показать ответ и решение

Наименьшее значение функции достигается при x =4 и равно

На рисунке изображен график функции определенной на интервале Найдите количество точек, в которых
производная функции f(x) равна 0.

Показать ответ и решение

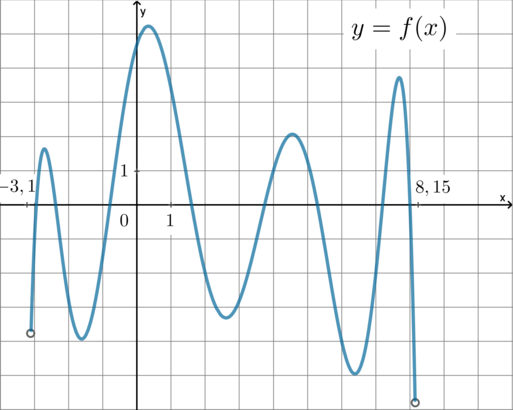
Производная равна нулю в точках экстремума функции. Таких точек пять:

На рисунке изображен график ′
y = f (x) — производной функции f(x), определённой на интервале Найдите
количество точек минимума функции f(x), принадлежащих отрезку

На рисунке изображен график функции определенной на интервале Найдите количество точек, в которых
касательная к графику функции f(x) параллельна прямой y = 12.

Показать ответ и решение

Если касательная параллельна прямой y = 12, то угловой коэффициент касательной равен угловому коэффициенту прямой
y = 12, то есть k = 0 и касательная горизонтальна.

Так как где — точка касания, и на рисунке изображен график функции, то на графике f(x) нужно найти
точки, в которых Это точки экстремума: их 7 штук.

На рисунке изображен график ′
y = f (x) — производной функции , определенной на интервале . В
какой точке отрезка [1,5;7] функция принимает наименьшее значение?

На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых
касательная к графику функции параллельна прямой y = 3 или совпадает с ней.

Показать ответ и решение

Так как на рисунке изображен график самой функции, то условие задачи нужно свести к функции.

Если касательная параллельна прямой y =3 , то угловой коэффициент касательной равен угловому коэффициенту прямой
y = 3 , то есть . Следовательно, yk = a , где — некоторое число.

Если — касательная к графику f(x) , то ее угловой коэффициент равен , где — абсцисса точки касания.
Количество таких точек нам и нужно найти.

Следовательно, . Но производная функции равна 0 в точках экстремума, следовательно, раз у нас
нарисован график самой функции, то нам нужно найти количество точек максимума и минимума. Таких точек у нас 7.

На рисунке изображен график — производной функции определенной на интервале Найдите
количество точек максимума функции принадлежащих отрезку

На рисунке изображен график — производной функции определенной на интервале Найдите
количество точек минимума функции принадлежащих полуинтервалу

Источник

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Экстремумы функции: признаки существования, примеры решений

Экстремумы функции, их необходимый и достаточный признаки

Локальный характер экстремумов функции

Ищем экстремумы функции вместе

Найти экстремумы функции самостоятельно, а затем посмотреть решение

Продолжаем искать экстремумы функции вместе

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.