В системе, показанной на рисунке, масса каждого бруска m=1 кг, жёсткость пружины k=20 Н/м, коэффициент трения между бруском и плоскостью x=0,4. Массы блока и пружины пренебрежимо малы. Система пришла в движение с нулевой начальной скоростью при недеформированной пружине. Найдите максимальную скорость брусков.
Записал уравнение:
[mg(1-мю) — k*дельта(x)]/2m = a = vdv/d(дельта(x))
Проинтегрировав, g(1-мю)*дельта(x) — (k*дельта(x)^2)/2m = v^2
A (силы трения) = мю*mg*дельта(x) = mv^2/2
Отсюда g(1-мю)*дельта(x) — (k*дельта(x)^2)/2m = 2*мю*mg*дельта(x)
Находим дельта x, подставляем в формулу для скорости, но получается неверный ответ. Подскажите, где я неправ?
Угол наклона плоскости к горизонту 30 град.
Распишем 2-ой закон Ньютона –
(с векторами) N + mg = ma;
Проекция на ось (тут без векторов) Ox: mg*sin(a) = ma(m сокращается)
g*sin(a) = a;
a = 10 * 1/2 = 5 м/с^2
x = x0 + V0x*t + ((ax*t^2)/2);
S = V0*t + ((a*t^2)/2)
V0 = (S – ((a*t^2)/2))/t
V0 = (12 – 5*4/2)/2 = 1 м/c
Гость4
Всего 1 ответ.
Другие интересные вопросы и ответы
Как найти скорость удаления? Формула удаления?
Как найти скорость удаления при движении в противоположные стороны?
Как найти скорость удаления при движении в одну сторону?
Как вычислить скорость удаления объектов друг от друга?
Therein6
В общем случае суммарная скорость удаления одного объекта от другого рассматривается в двух вариантах:
1)оба объекта двигаются в одном направлении.
2)оба объекта двигаются в разные стороны друг от друга.
3) мы тут не рассматриваем более сложный случай движения объектов под углом друг к другу.Хотя это очень распространённый вид движения.
1)в 1-м случае общая скорость(относительная) рассчитывается путём вычитания из большей скорости меньшую,
2) во 2-м случае относительная скорость рассчитывается путём сложения скоростей .
3) В этом случае относительная скорость рассчитывается путём сложения( вычитания )векторов.
Galina7v71
Всего 4 ответа.
Какие вещи знают люди вашей профессии, а другие люди, как правило, не знают?
Тоня Самсонова283
1) Эпилептические приступы часто бывают и без судорог, и без потери сознания, и без пены изо рта.
2) А шизофрения бывает без голосов и без бреда (простая шизофрения)
3) В психушке людей не “делают дураками” и там не всё так страшно, как принято считать.
4) При шизофрении не страдает интеллект.
5) Бредовые идеи могут охватывать и здоровых людей (индуцированный бред).
6) Шизофреники не считают и не называют себя Наполеонами.
7) Широко рекламируемый “Тенотен” и “Тенотен детский” – пустышка (смесь лактозы, целлюлозы и стеарата магния), основанная на плацебо-эффекте. Единственное его противопоказание – непереносимость лактозы.

Александр Стерлигов817
Всего 90 ответов.
Найти скорость бруска, пожалуйста, кто разбирается)
На неподвижной плоскости с углом наклона a=45° к горизонту находится брусок массой m=110г, прикреплённый к лёгкой пружине жёсткостью k=40 Н/м.
Брусок сдвигают вверх вдоль плоскости так, что пружина оказывается сжатой на l=5см и отпускают без начальной скорости.
Какую наибольшую скорость будет иметь брусок после того, как его отпустят? Ответ выразите в
м/с, округлив до десятых. Коэффициент трения между бруском и плоскостью составляет μ=0,6 Ускорение свободного падения g=10 м/с
Направления всех движений находятся в одной вертикальной плоскости.
Валерия Литвинова5
Может быть на подобии решения этой задачи?
Всего 1 ответ.
Брусок массой 1 кг соскальзывает без начальной скорости с вершины наклонной плоскости высотой 1 м и останавливается.
Гость4
Дано: масса m = 1 кг, высота h = 1м, ускорение свободного g =9,8 Н/м2
Работа силы трения F, остановившей брусок равна, потенциальной энергии бруска, которой он обладал, находясь на вершине.
Работа А = Δ Е = mgh = 1*9,8*1 = 9,8 Дж
Чтобы втащить брусок на вершину, нужно совершить такую же работу против сил трения и еще работу по поднятию бруска на вершину, т.е. 9,8 Дж * 2 = 19,6 Дж.
Дарья2
Всего 1 ответ.
Груз,
подвешенный на пружине, растягивает ее на 25 мм. Какова будет максимальная
скорость, если он будет совершать колебания вдоль вертикально направленной оси
с амплитудой, равной также 25 мм?
Решение.
Предположим,
что масса груза и жесткость пружины равны соответственно m и
k. Тогда для покоящегося груза, подвешенного на пружине, в состоянии равновесия выполняется равенство mg = kx0 , откуда k/m = g/x0 .
Если теперь этот
груз отклонить вверх или вниз от его положения равновесия, он начнет совершать
вдоль вертикальной оси OX гармонические
колебания. Действительно, если за x = 0 принять координату
точки, находясь в которой груз не деформирует пружину, то проекция на ось OX результирующей силы, действующей на груз, находящихся в точке x, будет равна mg – kx = kx0 – kx = —k(x – x0) = —kx’ , где x’ – x – x0 . Поскольку координаты
x’ и x отличаются
друг от друга только на постоянную величину x0 , проекции ускорения груза на оси OX и OX’ будут равны: ax = a’x
. Поэтому уравнение второго закона Ньютона, записанное в проекциях на ось OX’, принимает вид: ma’x = —kx, совпадающий с уравнением гармонических колебаний. Отсюда
следует, что груз будет совершать гармонические колебания.
Согласно
закону сохранения энергии максимальная кинетическая энергия тела, совершающего гармонические
колебания, равна его максимальной потенциальной энергии.
A – амплитуда колебаний.
Отсюда находим vmax .
Подставляем
сюда найденное выше выражение для k/m учитывая, что по условию задачи A
= x0 .
Ответ:
umax = 0,5 м/с.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
2021-03-13
На гладкой горизонтальной плоскости лежат два бруска массами $m_{1} = 400 г$ и $m_{2} = 100 г$, соединенные недеформированной пружиной. Первому бруску сообщают скорость $v_{1} = 10 м/с$ в направлении второго бруска. Найдите минимальную скорость этого бруска в процессе дальнейшего движения.
Решение:
Запишем законы сохранения импульса и энергии системы (рис.):
$m_{1}v_{1} = m_{1}u_{1} + m_{2}u_{2}$,
$frac{m_{1}v_{1}^{2} }{2} = frac{m_{1}u_{1}^{2} }{2} + frac{m_{2}u_{2}^{2} }{2} + frac{kx^{2} }{2}$,
где $x$ — деформация пружины. Главное для решения задачи — понять, чем интересующий нас момент, когда скорость бруска массой m1 минимальна, отличается от всех остальных моментов движения. Для этого надо рассмотреть действующие на первый брусок силы.
Как только брусок массой $m_{1}$ придет в движение, пружина начнет сжиматься, и на него будет действовать сила упругости, направленная навстречу движению. Предположим, что скорость этого бруска не меняет направления, т.е. что $u_{1}$ все время положительна (позже нам придется проверить это предположение). Тогда скорость $u_{1}$ будет уменьшаться по модулю до тех пор, пока на брусок действует сжатая пружина. Когда пружина перейдет в растянутое состояние, сила упругости будет направлена по движению, и скорость бруска начнет возрастать. Минимальная скорость соответствует тому моменту, когда пружина снова (как до начала движения) придет в недеформированное состояние, т.е. когда $x = 0$. В этот же момент скорость второго бруска будет максимальной.
Система уравнений в этот момент
$m_{1}v_{1} = m_{1}u_{1} + m_{2}u_{2}$,
$frac{m_{1}v_{1}^{2} }{2} = frac{m_{1}u_{1}^{2} }{2} + frac{m_{2}u_{2}^{2} }{2}$
совпадает с системой уравнений для центрального упругого удара (т.е. пружина как бы осуществляет растянутый по времени упругий удар). Решение этой задачи хорошо известно, мы приведем его без вывода:
$u_{1} = frac{m_{1} — m_{2}}{m_{1} + m_{2} } v_{1} = 6 м/с, u_{2} = frac{2m_{1} }{m_{1} + m_{2} } v_{1} = 16м/с$.
Если скорость $u_{2}$ всегда положительна, т.е. получен правильный ответ для максимальной скорости второго бруска при любом соотношении масс, то скорость $u_{1}$ остается положительной только при условии $m_{1} geq m_{2}$ . Если $m_{1} < m_{2}$, то в процессе движения скорость первого бруска меняет знак, и ответ для минимальной скорости такой: $u_{1} = 0$.
Отметим интересное отличие этой задачи от центрального упругого удара, например, двух шаров. Шары после удара перестают взаимодействовать и разлетаются. В нашем же случае пружина, соединяющая бруски, после рассмотренного момента растягивается, первый брусок начинает тормозиться, второй — разгоняться. Через некоторое время скорость первого бруска достигнет максимального значения $u_{1}^{ prime}$, а скорость второго — минимального $u_{2}^{ prime }$. Пружина в этот момент опять не деформирована, т.е. эти скорости подчиняются той же самой системе уравнений. Поскольку скорости должны отличаться от найденных, они представляют собой второе решение этой системы, которое в задаче о центральном упругом ударе отбрасывают: $u_{1}^{ prime} = v_{1}, u_{2}^{ prime } = 0$.
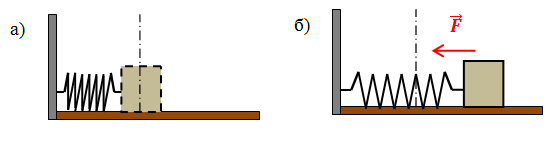
Пружинный маятник
Определения и формулы пружинного маятника
Рис.1. Пружинный маятник: а) в положении равновесия; б) в состоянии колебаний
Когда пружина не деформирована, тело находится в положении равновесия (рис.1,а). Если растянув или сжав пружину, вывести тело из положения равновесия, на него будет действовать сила упругости со стороны деформированной пружины. Эта сила направлена к положению равновесия и в данном случае является возвращающей силой.
Сила упругости в пружинном маятнике
Сила упругости пропорциональна смещению тела (удлинению пружины):
здесь — коэффициент жесткости пружины.
В положении, соответствующем максимальному отклонению тела от положения равновесия (смещение тела равно амплитуде колебаний) сила упругости максимальна, поэтому максимально и ускорение тела. По мере приближения тела к положению равновесия удлинение пружины уменьшается, и, следовательно, уменьшается ускорение тела, которое обусловлено силой упругости. Достигнув положения равновесия, тело не остановится, хотя в этот момент сила упругости равна нулю. Скорость тела в момент прохождения им положения равновесия имеет максимальное значение, и тело по инерции будет двигаться дальше, растягивая пружину. Возникающая при этом сила упругости будет тормозить тело, так как теперь она направлена в сторону, противоположную движению тела. Дойдя до крайнего положения, тело остановится и начнет движение в противоположном направлении. Движение тела будет повторяться в описанной последовательности.
Таким образом, причинами свободных колебаний пружинного маятника является сила упругости деформированной пружины (возвращающая сила) и инертность тела.
Период свободных колебаний пружинного маятника
Период свободных колебаний пружинного маятника определяется по формуле:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |