Как найти скорость чего либо

Была ли эта статья полезной?

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

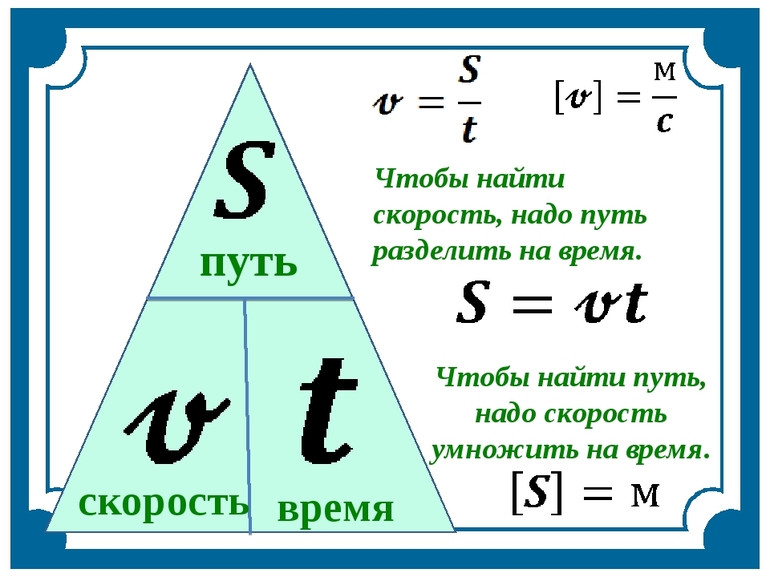
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

• S — расстояние (путь), пройденное материальной точкой или телом (м);
• T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

• неравномерную;
• среднюю;
• равномерно-переменную;
• поступательную;
• вращательную;
• ускоренную.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

• V0 — начальная скорость;
• A — ускорение (имеет постоянное значение);
• t — время движения.

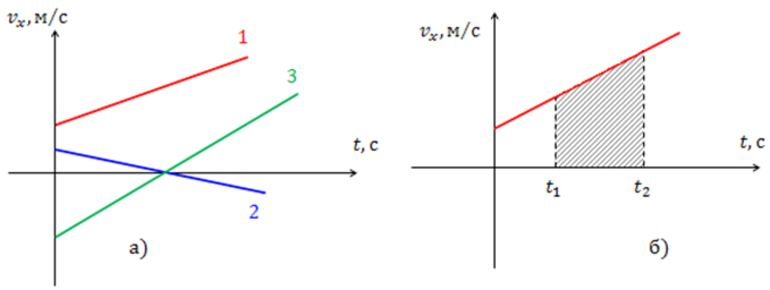
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r^-1(t). То есть, с математической точки зрения, это первая производная.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t²/2 = (V² — V²0) /2*A.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V²0 — 2* A * s)^½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)^½.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

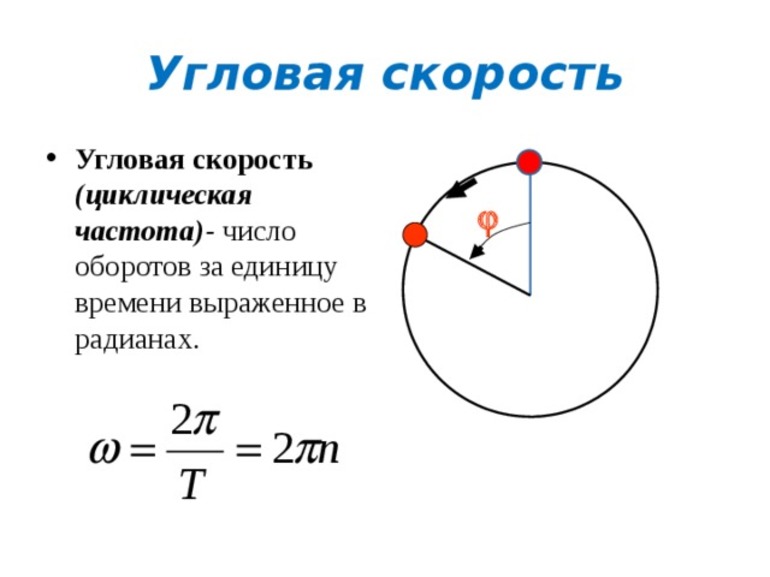
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

1. Справочный портал «Калькулятор».
2. Allcalc.
3. Fxyz.

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.

Расстояние

Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).

Расстояние связано со скоростью и временем:

S=v cdot t

Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.

Единицы длины	СИ
1 сантиметр	0,01 м
1 километр	1000 м
1 дециметр	0,1 м
1 миллиметр	0,001 м
1 микрометр	1·10-6 м
1 миля	1609,34 м
1 фут	0,3048 м
1 ярд	0,9144 м
1 дюйм	0,0254 м
1 морская миля	1852 м

Время

Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.

Время можно найти по формуле:

t=frac{S}{v}

Скорость

Скорость обозначается буквой  — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.

Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.

Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.

Формула скорости

Скорость можно найти через расстояние и время по формуле:

v=frac{S}{t}

Средняя скорость

Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.

Формула средней скорости:

v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}

То есть средняя скорость это отношение всего пути, ко всему времени.

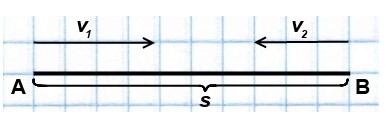
Скорости сближения и удаления

Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.

Скорость удаления

Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.

Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:

3+4=7 км/ч.

Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.

Формула скорости удаления:

v_{удаления}=v_1+v_2

где — скорость одного тела,

— скорость другого тела.

Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.

Скорость сближения двух тел

Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.

Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.

Формула скорости сближения:

v_{сближения}=v_1+v_2

где  — скорость одного тела,

 — скорость другого тела.

Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.

То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (=5 км/ч), то скорость их сближения будет 2 км/ч:

Формула скорости сближения при движении вдогонку:

v_{сближения}=v_1-v_2

где  — скорость одного тела,

 — скорость другого тела. При этом

Таблица «скорость, время, расстояние» при решении задач на движение

При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.

Скорость, v, м/с

Время, t, с

Расстояние, S, м

Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.

Составляем таблицу и записываем в нее данные:

Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
?	5	45

Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.

Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))

Рассмотрим теперь некоторые примеры решения задач

Примеры задач на движение

Задача 1

Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?

Решение:

Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.

Школьник дойдет до дома за полчаса.

Ответ: 0,5 ч.

Задача 2

Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?

Решение: Составим таблицу

	Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
Автомобилист	50	100/50	100
Велосипедист	x	100/x	100

Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:

displaystyle frac{100}{x}-frac{100}{50}=8

Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.

Решим полученное уравнение.

displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10

Ответ: 10 км/ч

Задача 3

Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.

Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.

В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:

0,05 cdot 60=3 c.

Тогда displaystyle v= frac{180}{3}=60 м/с.

Ответ: 60 м/с

Задача 4

Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?

Решение:

Определим весь путь который прошел турист:

displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.

Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч

Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч

Тогда найдем среднюю скорость:

displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.

Ответ: displaystyle v_{ср}=4 frac{2}{7}

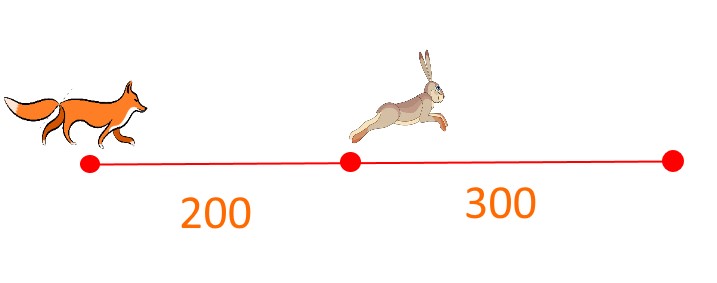
Задача 5

Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?

Решение:

Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.

Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.

Лиса не догонит зайца.

Действительно, скорость сближения лисы и зайца:

displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с

То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с

Заяц же уже 20 секунд будет в безопасном месте.

Ответ: лиса зайца не догонит.

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

F — сила,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Расчёт скорости по расстоянию и времени

Похожие калькуляторы