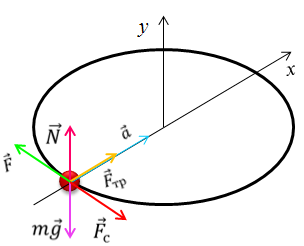
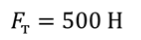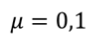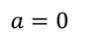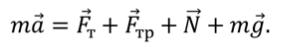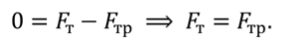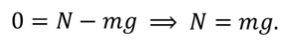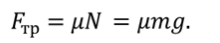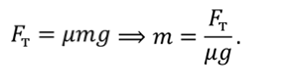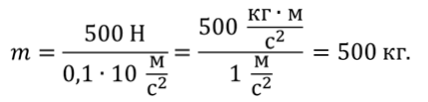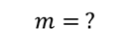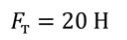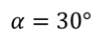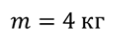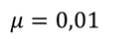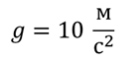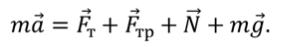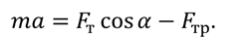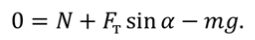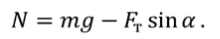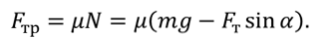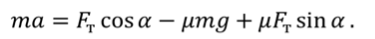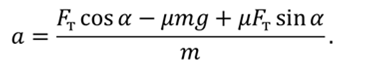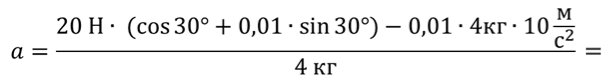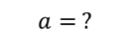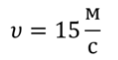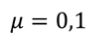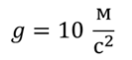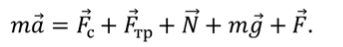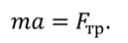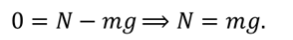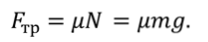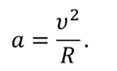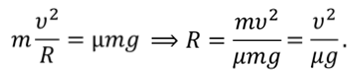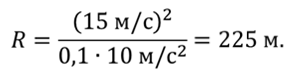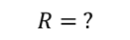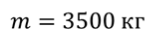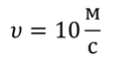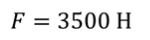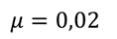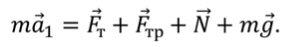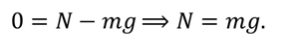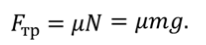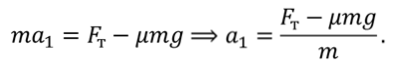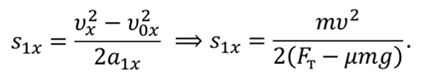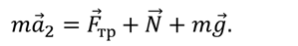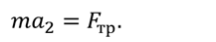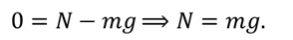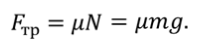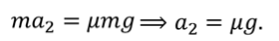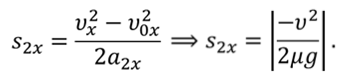Движение тела под действием силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ — тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline_ $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Так как сила трения $overline_ $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline_ right|$, то:
Но ускорение определяется также формулой:
где $v_ <0>$- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
Так как $F_ =mu mg$, подставим в формулу (1) и получим:
Выразив из формулы (2) $v_ <0>$найдем величину искомой скорости:
Ответ: Скорость автомобиля до выключения двигателя $v_ <0>=20$ м/с.
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_ <0>=20$м/с, $t=40$с.
Решение:
Уравнение движения сноубордиста будет иметь вид:
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
Так как сила трения $overline_ $равна $F_ =mu Bg$, находим коэффициент трения $mu $:
Ответ: $F_ =40H$, $mu =0,05$.
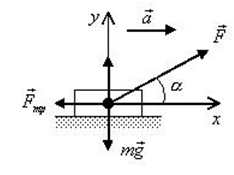
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Решение:
Уравнение движения тела:
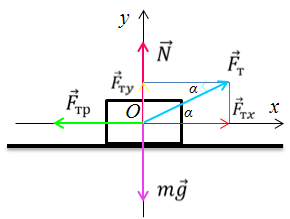
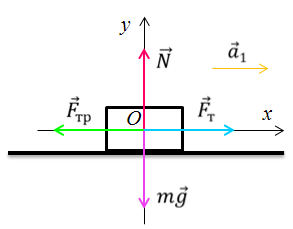
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
Поскольку $F_ =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_ =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
Силы трения. Коэффициент трения. Движение тела с учетом силы трения
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет.
Получите невероятные возможности
Конспект урока «Силы трения. Коэффициент трения. Движение тела с учетом силы трения»
«Любую задачу реально выполнить,
если разбить ее на выполнимые части»
Данная тема будет посвящена решению задач на силы трения и изучению движение тела с учетом сил трения.
Задача 1. Упряжка ездовых собак может тянуть по снегу сани с максимальной силой 500 Н. Какой массы саней с грузом может перемещать данная упряжка собак, двигаясь равномерно, если коэффициент трения саней о снег составляет 0,1?
Запишем второй закон Ньютона
В проекциях на ось Ох:
В проекциях на ось Оу:
Тогда искомая масса равна
Ответ: 500 кг.
Задача 2. Мальчик начинает тянуть санки по снегу, прилагая силу 20 Н, направленную под углом 30 о к горизонту. Определите ускорение, с которым движутся санки, если их масса равна 4 кг, а коэффициент трения между санками и снегом равен 0,01.
Запишем второй закон Ньютона
В проекциях на ось Ох:
В проекциях на ось Оу:
Из последнего уравнения выразим значение силы нормальной реакции опоры
Сила трения определяется по формуле
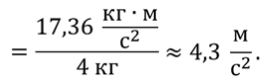
Тогда ускорение санок равно
Ответ: 4,3 м/с 2 .
Задача 3. Определите наименьший радиус поворота, который может сделать автомобиль, движущийся со скоростью 15 м/с, если коэффициент трения между шинами автомобиля и дорогой равен 0,1.
Запишем второй закон Ньютона для рассматриваемого случая
В проекциях на ось Ох:
В проекциях на ось Оу:
Сила трения определяется по формуле
Центростремительное ускорение определяется по формуле
С учётом последней формулы получаем
Ответ: 225 м.
Задача 4. Автомобиль массой 3500 кг, разгоняясь из состояния покоя, достигает скорости 10 м/с, а затем продолжает движение с выключенным двигателем до полной остановки. Определите весь путь, пройденный автомобилем за время движения, если сила тяги двигателя составляет 3500 Н, а коэффициент трения шин о дорогу равен 0,02.
Запишем второй закон Ньютона
В проекциях на ось Ох:
В проекциях на ось Оу:
Сила трения определяется по формуле
Путь, пройденный автомобилем на разгонном участке
Перейдем к рассмотрению второго участка движения автомобиля — участка торможения
Запишем второй закон Ньютона для второго участка
В проекциях на ось Ох:
В проекциях на ось Оу:
Сила трения определяется по формуле
Длина участка торможения:
Весь путь, пройденный автомобилем, складывается из длин участков разгона и торможения
Как найти начальную скорость,если известно расстояние и коэффициент трения
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
1. Дано действительное число – цена 1 кг конфет. Вывести стоимость 0,5; 1; 1,5 … 10 кг конфет. (Подсказка – используем цикл WHILE).
Программа должна иметь следующий вид:
Компьютер запрашивает стоимость одного килограмма конфет.
Пользователь вводит стоимость одного килограмма конфет, и компьютер выводит на экран:
Сила трения. Коэффициент трения
При движении одного тела по поверхности другого всегда возникает сила, направленная противоположно направлению скорости и замедляющая движение. Эта сила называется силой трения.
По своей природе сила трения отличается от силы тяготения и силы упругости, которые были рассмотрены в предыдущих параграфах.
Причины возникновения силы трения можно разделить на два класса: 1) шероховатость поверхностей контактирующих тел; 2) взаимное притяжение молекул при контакте.
Неровности поверхностей проявляются на макроуровне и видны невооруженным глазом или в оптический микроскоп. Их влияние можно уменьшить, если отполировать поверхности или нанести смазку.
Взаимное притяжение молекул проявляется на микроуровне и приводит к тому, что даже на идеально отполированных поверхностях не удается избежать трения, когда частицы одного тела перемещаются относительно частиц другого.
Как и сила упругости, сила трения имеет электромагнитную природу и связана с межмолекулярным взаимодействием.
Но в отличие от силы упругости, причиной силы трения является разрыв межмолекулярных связей. Кроме того, если сила упругости всегда направлена перпендикулярно поверхностям контактирующих тел, то сила трения всегда направлена вдоль этих поверхностей.
В зависимости от характера движения контактирующих тел различают трение покоя, трение скольжения и трение качения.
п.2. Трение покоя
Пример изменения силы трения покоя
 |
Сила трения покоя равна приложенной силе, которая все ещё не приводит тело в движение. Допустим, что мы прикладываем к шкафу последовательно силу 100 Н, 200 Н, 300 Н, и он начинает равномерно двигаться только при 300 Н. Как только тело начинает скользить, на него уже действует сила трения скольжения. Получаем: |
||
| Приложенная сила, Н | Движение | Сила трения покоя, Н | Сила трения скольжения, Н |
| 100 | Нет | 100 | — |
| 200 | Нет | 200 | — |
| 300 | Есть, равномерное | — | 300 |
п.3. Трение скольжения
 |
Если тело расположено на горизонтальной опоре, сила тяжести (mg), действующая на него, равна по величине силе реакции опоры (N) (см. §22 данного справочника). Сила трения направлена противоположно силе тяги. |
Значения коэффициентов трения скольжения для различных поверхностей приводятся в справочных таблицах.
При проектировании и разработке машин и механизмов коэффициенты трения скольжения для отдельных узлов определяются в специальных лабораториях.
п.4. Трение качения
Сила трения качения значительно меньше силы трения скольжения.
 |
Уменьшение трения за счет качения используется в шариковых и роликовых подшипниках. Первый подшипник качения был установлен в опоре ветряка, построенного в Англии в 1780 г. Этот подшипник состоял из двух литых чугунных дорожек качения, между которыми находилось 40 чугунных шаров. Сегодня подшипники являются незаменимой деталью во всех подвижных конструкциях; они уменьшают износ трущихся деталей и снижают потери энергии на нагрев из-за трения. |
п.5. Задачи
Задача 1. Найдите коэффициент трения между шинами автомобиля и дорогой, если при равномерном движении по прямолинейному участку двигатель развивает силу тяги, равную 30 кН. Масса автомобиля 6 т.
Коэффициент трения $$ mu=frac>>. $$ При равномерном движении скорость постоянна и ускорение (overrightarrow=0). По второму закону Ньютона, равнодействующая горизонтальных сил равна нулю $$ overrightarrow>>+ overrightarrow>>=0. $$ Значит, сила трения и сила тяги равны по модулю: $$ F_<text<тр>>=F_<text<тяги>>. $$ Сила реакции горизонтальной опоры равна силе тяжести, действующей на автомобиль: $$ n=mg. $$ Получаем: $$ mu=frac>>= frac>>, mu=frac<3cdot 10^4><6cdot 10^3cdot 10>=0,5. $$ Ответ: 0,5
Задача 2. Деревянный брусок массой 3 кг равномерно тянут по горизонтальной деревянной доске с помощью динамометра. Жесткость пружины динамометра равна 3 Н/см, коэффициент трения дерева об дерево 0,3. На сколько сантиметров растянется пружина?
Показания динамометра – это сила упругости, равная силе тяги. При равномерном движении сила тяги равна по модулю силе трения. Поэтому begin F_<text<упр>>=kDelta l=F_<text<тр>>=mu N=mu mgRightarrow kDelta l=mu mg end Получаем: $$ Delta l=frac<mu mg>, Delta l=frac<0,3cdot 3cdot 10><300>=0,03 (text<м>)=3 (text<см>) $$ Ответ: 3 см.
Задача 3. Автомобиль движется по горизонтальному участку дороги со скоростью 72 км/ч. Рассчитайте время торможения и тормозной путь до полной остановки, если коэффициент трения колес о дорогу равен 0,4.
Автомобиль тормозит за счет силы трения. По второму закону Ньютона begin F_<text<тр>>=ma. end С другой стороны на горизонтальной дороге $$ F_<text<тр>>=mu N=mu mg. $$ Получаем: $$ ma=mu mgRightarrow a=mu g. $$ По определению ускорения $$ a=frac. $$ Т.к. (v_2=0), ускорение отрицательное.
Модуль ускорения $$ |a|=frac=mu gRightarrow t=frac <mu g>$$ Время торможения прямо пропорционально скорости и обратно пропорционально коэффициенту трения. $$ t=frac<20><0,4cdot 10>=5 (text<с>) $$ Найдем тормозной путь $$ s=v_1t+frac<2>=v_1t+ left(frac<overbrace^<=0>-v_1>right)frac<2>=v_1t -frac<2>=frac<2>=frac<2>cdot frac<mu g>=frac <2mu g>$$ Тормозной путь прямо пропорционален квадрату(!) скорости и обратно пропорционален коэффициенту трения. $$ s=frac<20^2><2cdot 0,4cdot 10>=50 (text<м>) $$ Ответ: 5 с; 50 м.
п.6. Лабораторная работа №8. Измерение коэффициента трения скольжения
Цель работы
Научиться измерять силу трения скольжения и определять коэффициент трения скольжения. Изучить зависимость коэффициента трения скольжения от материалов соприкасающихся тел и от площади опоры движущегося тела.
Теоретические сведения
 |
При (v=const) (равномерное движение) получаем По вертикали (moverrightarrow=-overrightarrow). Модули этих сил равны По горизонтали (overrightarrow>>=-overrightarrow>>). Модули этих сил равны $$ F_<text<тяги>>=F_<text<тр>>=mu N=mu mg $$ |
Если тело перемещать с помощью динамометра, то сила упругости, возникающая в пружине, будет равна силе тяги. Т.е., сила тяги непосредственно измеряется динамометром.
В работе используются стандартные лабораторные грузики массой 100 г.
Измерив силу тяги и зная массу перемещаемого тела, рассчитываем коэффициент трения: $$ mu=frac>> $$
Для расчетов используем стандартное значение (g=9,80665 text<м/с>^2).
Погрешность для прямых измерений (F_<text<тяги>>) определяется как половина цены деления динамометра. Погрешность для массы определяется по маркировке грузиков и бруска, (Delta m=2 text<г>) для (m=100 text<г>), т.е. (delta_m=2text<%>).
Погрешность эксперимента (delta_e) рассчитывается как средняя арифметическая по результатам измерений и вычислений.
Приборы и материалы
Лабораторный динамометр на 5 Н; набор грузиков по 100 г; деревянный брусок с крючком 100 г; деревянная доска; наждачная бумага.
Ход работы
1. Прикрепите динамометр к бруску, положите доску горизонтально, поставьте брусок самой большой по площади гранью слева на доску.
2. Перемещая брусок слева направо по доске, добейтесь равномерного скольжения (со стабильными показаниями динамометра). Снимите показания динамометра и запишите.
3. Повторите эксперимент, нагружая брусок одним, двумя, тремя и четырьмя грузиками.
4. Рассчитайте коэффициент трения дерева об дерево, определите относительную и абсолютную погрешности эксперимента.
5. Повторите эксперимент, перемещая брусок по доске, обмотанной наждачной бумагой. Найдите коэффициент трения дерева об наждак, определите относительную и абсолютную погрешности эксперимента.
6. Снимите наждачную бумагу и повторите эксперимент для трения дерева об дерево. Однако на этот раз брусок должен опираться на меньшую по площади грань. Рассчитайте коэффициент трения дерева об дерево в этом случае.
7. Сравните полученные коэффициенты трения, сделайте выводы о зависимости коэффициента трения от материала соприкасающихся поверхностей и от площади опоры движущегося тела.
Результаты измерений и вычислений
Цена деления динамометра (d=0,1 text<Н>).
Таблица для расчета коэффициента трения скольжения дерева об дерево
| Опыт | (m, text<кг>) | (F_<text<тяги>>, text<Н>) | (mu=frac>>) | (Delta=|mu-mu_<text<ср>>|) | |
| 1 | Брусок | 0,1 | 0,3 | 0,306 | 0,026 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,025 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,008 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,001 |
| 5 | Брусок + 4 грузика | 0,5 | 1,6 | 0,326 | 0,006 |
| Всего | — | — | 1,660 | 0,065 |
Среднее значение коэффициента трения $$ mu_<text<ср>>=frac<1,660><5>=0,332 $$ Среднее значение абсолютного отклонения $$ Delta =frac<0,065><5>=0,013 $$ Относительная погрешность begin delta=frac<0,013><0,332>cdot 100text<%>approx 3,9text<%>\[7pt] mu_<text<дд>>=(0,332pm 0,013), delta_mu=3,9text <%>end
Таблица для расчета коэффициента трения скольжения дерева об наждак
| Опыт | (m, text<кг>) | (F_<text<тяги>>, text<Н>) | (mu=frac>>) | (Delta=|mu-mu_<text<ср>>|) | |
| 1 | Брусок | 0,1 | 0,6 | 0,612 | 0,039 |
| 2 | Брусок + 1 грузик | 0,2 | 1,1 | 0,561 | 0,012 |
| 3 | Брусок + 2 грузика | 0,3 | 1,7 | 0,578 | 0,005 |
| 4 | Брусок + 3 грузика | 0,4 | 2,2 | 0,561 | 0,012 |
| 5 | Брусок + 4 грузика | 0,5 | 2,7 | 0,551 | 0,022 |
| Всего | — | — | 2,862 | 0,090 |
Среднее значение коэффициента трения $$ mu_<text<ср>>=frac<2,862><5>approx 0,572 $$ Среднее значение абсолютного отклонения $$ Delta =frac<0,090><5>=0,018 $$ Относительная погрешность begin delta=frac<0,018><0,572>cdot 100text<%>approx 3,1text<%>\[7pt] mu_<text<дн>>=(0,572pm 0,018), delta_mu=3,1text <%>end
Таблица для расчета коэффициента трения скольжения дерева об дерево (узкая грань)
| Опыт | (m, text<кг>) | (F_<text<тяги>>, text<Н>) | (mu=frac>>) | (Delta=|mu-mu_<text<ср>>|) | |
| 1 | Брусок | 0,1 | 0,35 | 0,357 | 0,011 |
| 2 | Брусок + 1 грузик | 0,2 | 0,7 | 0,357 | 0,011 |
| 3 | Брусок + 2 грузика | 0,3 | 1,0 | 0,340 | 0,006 |
| 4 | Брусок + 3 грузика | 0,4 | 1,3 | 0,331 | 0,015 |
| 5 | Брусок + 4 грузика | 0,5 | 1,7 | 0,347 | 0,000 |
| Всего | — | — | 1,732 | 0,043 |
Среднее значение коэффициента трения $$ mu_<text<ср>>=frac<1,732><5>approx 0,346 $$ Среднее значение абсолютного отклонения $$ Delta =frac<0,043><5>approx 0,009 $$ Относительная погрешность begin delta=frac<0,009><0,346>cdot 100text<%>approx 2,5text<%>\[7pt] mu ‘_<text<дд>>=(0,346pm 0,009), delta_mu=2,5text <%>end
Выводы
На основании проделанной работы можно сделать следующие выводы.
В работе исследовалась зависимость коэффициента трения скольжения от поверхностей, из которых изготовлены соприкасающиеся тела.
Для скольжения дерева об дерево был получен коэффициент begin mu_<text<дд>>=(0,332pm 0,013), delta_mu=3,9text <%>end
Для скольжения дерева об наждак был получен коэффициент begin mu_<text<дн>>=(0,572pm 0,018), delta_mu=3,1text<%>\[7px] mu_<text<дн>>gt mu_<text<дд>> end
Наждак является более шероховатой поверхностью и сила трения на ней больше.
Коэффициент трения скольжения сильно зависит от материалов соприкасающихся поверхностей.
Также в работе исследовалась зависимость коэффициента трения скольжения от площади опоры движущегося тела. Брусок выставлялся на более узкую грань, и изучалось скольжение дерева об дерево в этом случае. Был получен коэффициент begin mu’_<text<дд>>=(0,346pm 0,009), delta_mu=2,5text <%>end Поскольку begin 0,319le mu_<text<дд>>le 0,345 0,337le mu’_<text<дд>>le 0,355 end Полученные отрезки значений перекрываются.
Таким образом, в рамках погрешности эксперимента коэффициент трения скольжения не зависит от площади опоры движущегося тела.
8. Истечение жидкости через отверстия и насадки при постоянном напоре.
8.1. Истечение через отверстия при постоянном напоре.
8.2. Истечение при совершенном сжатии. Скорость истечения реальной жидкости при совершенном сжатии.
8. 3. Коэффициенты: ξ, φ, μ
8.3. Истечение при несовершенном сжатии
8.4. Истечение под уровень
8.5. Истечение через насадки при постоянном напоре.
8.5.1.Первый режим течения.
8.5.2 Второй режим истечения
Рекомендуемые материалы
Отверстия и насадки, из которых происходит истечение, могут иметь различное конструктивное исполнение и назначение.
Перелив жидкости из бака в бак производится через отверстия между баками, которые закрываются запорными элементами.
Насадки применяются в моечных устройствах и двигателях, где с их помощью производится распыление жидкости. Такие насадки являются сложным изделием, имеют предкамеру высокого давления, запирающую иглу, которой открывается отверстие вначале впрыска на неполное сечение и открывается полностью к концу сжатия, чтобы обеспечить нормальный режим сгорания топлива в цилиндре.
Компактная и сильная струя для брандспойта или гидромонитора формируется при помощи насадков.
В устройствах гидроавтоматики: золотниках и элементах типа «сопло-заслонка» применяются соотношения, полученные в теории истечения.
При переходе потенциальной энергии жидкости в резервуаре в кинетическую энергию струи, часть энергии теряется на трение и завихрение частиц жидкости.
Задачей изучения истечения является определение скоростей истечения, расхода и давления жидкости в отверстиях и насадках и их техническое применение.
8.1. Истечение через отверстия при постоянном напоре .
Истечение из резервуара при постоянном напоре и под давлением Р1 над свободной поверхностью через круглое отверстие с острой кромкой.
Через отверстие струя жидкости вытекает в воздушное пространство с атмосферным давлением Р2 =Рат.
Глубина расположения отверстия в дне или на стенке резервуара во много раз больше диаметра отверстия Н0 >> dо (рис.8.1).
К отверстию жидкость подтекает со всех сторон, поэтому в плоскости отверстия частицы движутся по криволинейным траекториям, поэтому за отверстием площадь сечения струи оказывается меньше площади отверстия, происходит сжатие струи. В дальнейшем струя сохраняет свою форму на некотором расстоянии от отверстия.
1. Сжатие струи называется совершенным, если стенки резервуара удалены от центра отверстия на расстояние l > 3d и не оказывают влияния на сжатие струи. В этом случае сечение струи получается наименьшим.
2.Сжатие струи называется несовершенным при l < 3d. в этом случае влияние стенок резервуара на сжатие струи значительно меньше и сечение струи оказывается больше, чем при совершенном сжатии.
8.2. Истечение при совершенном сжатии. Скорость истечения реальной жидкости.
Сжатие струи оценивается коэффициентом сжатия ε, равным отношению площади поперечного сечения струи к площади отверстия
ε = Sc/S0 = (dc/d0)2. (8.1)
Коэффициент сжатия зависит от 1)формы отверстия; 2)положения отверстия относительно стенок резервуара, например, в центре симметрии дна или смещенное от центра и от 3) числа Рейнольдса 
Влияние числа Рейнольдса на коэффициент сжатия показывает график Альтшуля.
Для определения скорости в сжатом сечении запишем уравнение Бернулли для живого сечения, соответствующего свободной поверхности жидкости в резервуаре «1-1» и сжатого сечения струи «2 –2», плоскость сравнения выберем по сечению «2-2».

Определим напоры, входящие в уравнение Бернулли.
1. Рассматривается установившееся движение, уровень жидкости не меняется, истечение происходит под постоянным напором: следовательно: геометрический напор z1 =H.
2. Давление Р1 на поверхности «1-1» может быть равно атмосферному, больше или меньше атмосферного, поэтому пьезометрический напор равен Р1/ρg.
3. Поскольку уровень жидкости в сечении «1-1» не меняется, скорость V1 = 0 равна нулю.
4. По сечению «2-2» выбрана плоскость сравнения, поэтому геометрический напор равен z2=0.
5. Истечение происходит в атмосферу, поэтому избыточное давление в сечении 2-2″ Р2 = Ратм = Рс = 0, пьезометрический напор равен Р2/ρg = 0.
6. Скорость в сжатом сечении V2 = Vc.
7. При ламинарном режиме движения эпюра скоростей близка к параболической, коэффициент Кариолиса принимается равным двум αл ≈2, при турбулентном режиме движении эпюра близка к трапециидальной αт ≈ 1-1,1 приниманется в расчетах равным единице.
С учетом этих допущений и исходных данных для турбулентного режим течения уравнение Бернулли для сечений «1-1» и «2-2»,принимает вид
где ζ — коэффициент сопротивления отверстия, α — коэффициент Кориолиса,
Н = Н1 + Р1 / ρg — напор истечения, сумма геометрического и пьезометрического напора, 
Коэффициент скорости при совершенном сжатии
8.3. Коэффициенты:ε, ζ, φ, μ
В уравнении Бернулли для идеальной жидкости из-за отсутствия вязкости нет потерь на трение, и коэффициенты сопротивления равен ξ = 0, при α = 1, φ = 1. Скорость истечения идеальной жидкости из отверстия с острой кромкой

Коэффициент скорости φ для реальной вязкой жидкости можно определить, поделив скорость истечения реальной жидкости в сжатом сечении 


Коэффициент φ равен отношению скорости истечения реальной жидкости к скорости истечения идеальной жидкости. Коэффициент φ < 1 из-за наличия вязкости у реальной жидкости.
Умножив площадь сечения сжатой струи Sc = εSо на скорость струи в сжатом сечении 

Коэффициентом расхода при истечении из отверстия μ называется произведение коэффициента сжатия ε на коэффициент скорости φ
μ = ε * φ. (8.7)
Расхода через отверстие с острой кромкой при совершенном сжатии


где Н- напор истечения или расчетный напор, а ΔР=(р1-Р2)/ρg — расчетная разность давлений, под действием которой происходит истечение.
По этим формулам определяется расход истечения из отверстия с острой кромкой и через насадки различных форм.
На рис. 8.4 показаны составленные А.Д. Альтшулем зависимости для коэффициентов ε, φ и μ для круглого отверстия в функции числа Rе.
1.Увеличение числа 

2. Коэффициент ε уменьшается из-за уменьшения торможения жидкости у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую часть. При Rе →∞ значения коэффициентов приближаются к φ→1 и ε→0,6.
3 Коэффициент расхода равный произведению μ = ε * φ с увеличением Re сначала растет, что связано с ростом φ, а затем уменьшается в связи со значительным падением ε, при больших Rеи равен μ = 0,60÷0,62.
4. В области малых Re (Rеи < 25) роль вязкости велика, торможение жидкости у кромки значительно, сжатие струи почти отсутствует и ε = 1, φ = μ.
При числах Re <23 для определения μ можно пользоваться формулой:

5.При увеличении скорости и числах Рейнольдса Re> 105 , Re почти не влияет на коэффициенты истечения (квадратичная зона истечения), для расчетов можно пользоваться средними значениями: φ = 0,97; ε= 0,62; μ = 0,60.
При турбулентном режиме движения неравномерность средних скоростей в сжатом сечении струи невелика, αт = 1, при φ = 0,97 можно принимать в среднем для круглого отверстия с острой кромкой при несовершенном сжатии

6.Коэффициент полезного действия отверстия — отношение удельной кинетической энергии струи к напору истечения:


7. При больших Re α=1, КПД равен 
8. Для малых отверстий некруглой формы при больших Re значения коэффициента расхода в формуле для определения расхода можно принимать равными μ= 0,6.
8.4. Истечение при несовершенном сжатии
Сжатие струи называется несовершенным, когда на формирование струи оказывает влияние близость боковых стенок резервуара, то есть расстояние от оси отверстия до стенки l < 3d. Сечение резервуара соизмеримо с сечением отверстия.
Боковые стенки успевают сформировать поток жидкости при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.
1. При несовершенном сжатии и больших числах Re коэффициент сжатия ε1 определяется по формуле
ε1 = 0,62 +0,38/(S0/S1) (8.15)
где S0/S1 отношение площади отверстия S0 к площади S1 поперечного сечения резервуара.
2. Коэффициент скорости при несовершенном сжатии φ находят по графику Альтшуля на рис.8.3 по числу Re.
3. Коэффициент сопротивления отверстия ζ можно найти из формулы, связывающей 
4. Коэффициент расхода при несовершенном сжатии равен μ1 = ε1 φ .
Используем уравнение Бернулли для определения коэффициентов истечения при несовершенном сжатии.


За плоскость сравнения возьмем сечение 2. Исходные данные по сечению «1-1»: z1=h, P/ρg, V1. Исходные данные по сечению «2-2»: z2=0, P2=Pатм =0, V1=Vс-скорость в сжатом сечении, S2 = Sc = ε1S0. Напор истечения равен :
Выразим V1 через V2 : 

4.Cкорость в сжатом сечении при несовершенном сжатии струи

5.Расход для несовершенного сжатия струи

8.5. Истечение под уровень
Истечением жидкости в пространство, заполненное этой же жидкостью, называется истечением под уровень (рис. 8.6). Кинетическая энергия струи теряется на вихреобразование.
Определим скорость и расход, используя уравнение Бернулли для поверхности «1- 1» и сечения «2 – 2», за плоскость сравнения принято – сечение «1-1».
Исходные данные: z1=h1, P1 > Ратм, V1 = 0 , в сечении «2-2» : z2=0, Р2в< Ратм,
P2 =- Р2в+ρgh2, скорость в сжатом сечении V2 →?, ξ ≈0,06 – коэффициент сопротивления отверстия принимают таким же, как при истечении в атмосферу, коффициента Кориолиса α.
Исходное уравнение

после подстановки исходных данных: 
где Н –напор истечения: разность гидростатических напоров по обе стороны стенки. Скорость и расход не зависят от высоты расположения отверстия.


где Sc – площадь сжатого сечения струи, S0 – площадь отверстия. Скорость и расход в этом случае определяются, как при истечении в атмосферу.
Значения коэффициентов истечения для затопленного отверстия можно принимать такими же, как при истечении свободной струи в атмосферу.
8.5. Истечение через насадки при постоянном напоре.
Внешним цилиндрическим насадком называется короткая трубка длиной, равной l = (1÷5)d с острой входной кромкой (рис.8.7). Истечение через такой насадок в атмосферу может происходить в двух режимах.
а) Безотрывной режим течения называется режим истечения, при котором струя после входа в насадок сначала сжимается, потом затем сжатая часть струи расширяется до размеров выходного диаметра и выходит сечением равным сечению насадка.
При истечении жидкости из больших резервуаров через насадки скорость истечения на выходе из насадка и расход определяются по формулам.
В формуле (6.6) F0 заменяется выходной площадью насадка Fн.
Для коноидального (плавно сужающегося насадка без сжатия струи на выходе)
ε = 1 можно принимать в квадратичной зоне сопротивления μ = φ = 0,97.
Коэффициенты истечения могут быть приближенно определены путем суммирования потерь на отдельных участках потока.
Так, например, для внешнего цилиндрического насадка (рис. 6.8) потерю напора можно представить в виде суммы:
где hп(1+x) потеря при входе в насадок на участке до сжатого сечения струи (х)’,hп(х+2) — потеря при расширении потока на участке между сжатым и выходным сечениями.
Предполагая турбулентный режим течения, и выражая эти потери по формулам
получим
где ζ0 — коэффициент сопротивления отверстия с острой кромкой; vx — скорость в сжатом сечении струи. По уравнению расхода

где Fx— площадь сжатого сечения; ε — коэффициент сжатия струи при входе в насадок.
Значение ε зависит от соотношения площадей насадка Fн и резервуара F1 и может быть определено по формуле ε1 = 0,62 +0,38/(S0/S1)2 (6.12).
Подставляя в выражение суммы потерь значение Vх, находим коэффициент сопротивления насадка

при помощи которого определяются скорость истечения и расход (сжатие струи на выходе из насадка отсутствует);
При истечении из большого резервуара (рис. 6.9) сжатие струи в сечении х является совершенным, и расчет дает в этом случае для средних значений ζ0 =0,06 и εx ζ=0,5. Скорость и расход определяются по формулам (6.1) и (6.6), в которых
Наглядное представление об изменениях напора потока и его составляющих при истечении жидкости через насадок дается графиком напоров (см. рис. 6.9). Линия напора и пьезометрическая линия на этом графике качественно изображают ход изменения полного и гидростатического напоров по длине насадка от начального сечения перед входом в насадок до его выходного сечения.
Пьезометрический напор рн /(ρg) в любом сечении насадка определяется расстоянием по вертикали от оси насадка до пьезометрической линии, скоростной напор v2 /(2g) — расстоянием по вертикали между пьезометрической линией и линией напора.
8. Если в промежуточных сечениях насадка скорости имеют большие значения, чем скорость выхода из насадка, то в этих сечениях при истечении в атмосферу возникает вакуум (пьезометрическая линия проходит здесь ниже оси насадка).
Так, например, наибольший вакуум рв, возникающий внутри цилиндрического насадка в сжатом сечении струи, определяется из выражения

Истечение через насадок в атмосферу с заполнением выходного сечения насадка возможно только при напорах, меньших предельного Hпр, который соответствует падению абсолютного давления в сжатом сечении до давления насыщенных паров жидкости (рx = рнп):

При Н ≥ Нпр происходит срыв режима работы насадка: струя отрывается от стенок, и процесс сменяется истечением через отверстие с острой кромкой.
При истечении через затопленный насадок его работа под более высоким напором, чем некоторое предельное значение (зависящее от заглубления насадка), сопровождается кавитацией.
Если истечение жидкости происходит под действием давления Р0 в среду газа с давлением Р2, расчетный напор в этом случае равен
H = (P0 – Р2)/(ρg)
В струе на выходе из насадка давление равно Р2, в суженном месте струи внутри насадка, где скорость увеличена, давление Р1 меньше, чем Р2. Чем больше напор, под которым происходит истечение и расход через насадок, тем меньше абсолютное давление Р1. Разность давлений Р2 — Р1 растет пропорционально напору Н.
Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 (см. рис.8.7),
Последний член уравнения представляет собой потерю напора на расширение потока, которое происходит примерно, как при внезапном расширении трубы.
Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε, как и в случае отверстия, поэтому на основании уравнения расхода

Заменив скорость V1 в уравнении Бернулли на скорость V2, и, использовав формулу 

Подставляя сюда φ = 0,8 и ε=0.63, получаем
(Р2 — Р1 ) ≈ 0,75ρgH (8.20)
Если истечение происходит в среду, где давление Р2 постоянно и равно атмосферному, увеличение напора приводит к уменьшению Р1 — абсолютное давление в сжатом сечении «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует величина напора, называемая критическим напором
Hкр ≈ Р2 /(0,75ρg). (8.21)
Следовательно, при Н > Hкр и постоянном Р2 давление Р1 должно стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому режим безотрывного истечения при Н > Hкр делается невозможным. При Н ≈ Hкр происходит изменение режима истечения и переход к отрывному режиму.
Если через насадок происходит истечение воды в атмосферу, то
Hкр ≈ Ра /(0,75ρg) = 10,33/0,75 ≈ 14 м.
Когда давление Рн.п. насыщенных паров истекающей жидкости соизмеримо с давлением Р2 среды, в которую происходит истечение, пренебречь величиной Рн.п. нельзя, в формуле (8.20) следует принять Р1 = Рн.п.
Hкр = (Ра – Рн.п.) /(0,75ρg) (8.22)
б) Отрывной режим истечения характеризуется тем, что струя после сжатия уже не расширяется, сохраняя цилиндрическую форму, и внутри насадка не соприкасается с его стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от безотрывного к отрывному скорость возрастает, а расход уменьшается, благодаря сжатию струи.
Если после перехода от первого режима истечения ко второму уменьшить напор Н, то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй режим истечения возможен при любых напорах, следовательно, при Н < Нкр возможны оба режима.
При истечении через цилиндрический насадок под уровень безотрывной режим истечения будет таким же. Когда абсолютное давление внутри насадка благодаря увеличению Н падает до давления насыщенных паров и перехода к отрывному течению не происходит, а начинается кавитационный режим, при котором расход перестает зависеть от противодавления Р2, и получается эффект стабилизации расхода. При этом чем меньше относительное противодавление Р2/Р0 = Рвых/Рвх =
Информация в лекции «27. Концентрация капитала во французской прессе» поможет Вам.
Коноидальный насадок (рис.8.8) выполняется по форме естественно сжимающейся струи и обеспечивает безотрывность течения внутри насадка и параллельность струй в выходном сечении. Этот насадок имеет коэффициент расхода, близкий к единице, и очень малые потери (коэффициент сжатия ε = 1), устойчивый режим течения без кавитации.
Значения коэффициента сопротивления ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим μ =φ= 0,99÷0,96.
Диффузорный насадок представляет собой комбинацию сопла и диффузора (рис. 8.8).
Приставка диффузора к соплу влечет за собой снижение давления в узком месте насадка, увеличение скорости и расхода жидкости через него. При том же диаметре узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать значительно больший расход (увеличение до 2,5 раза), чем сопло.
Такие насадки применяют, когда заданы диаметр узкого сечения и напор и требуется получить возможно больший расход. Однако, используют диффузорные насадки при небольших напорах Н = 1 ÷4 м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение сопротивления и уменьшение пропускной способности насадка.
Как рассчитать скорость
Современная жизнь проходит в постоянном движении: машины, поезда, самолеты, все торопятся, куда-то бегут, и часто бывает важно рассчитать скорость этого движения. Для расчета скорости есть формула V=S/t, где V – это скорость, S – расстояние, t – время. Рассмотрим пример, чтобы усвоить алгоритм действий.

Инструкция
Интересно узнать, с какой скоростью вы ходите? Выберите дорожку, метраж которой вы точно знаете (на стадионе, например). Засеките время и пройдите по ней в своем обычном темпе. Так, если длина пути 500 метров (0,5 км), и вы прошли ее за 5 минут, значит разделите 500 на 5. Получается, что ваша скорость 100 м/мин.
Если на велосипеде вы проехали ее за 3 минуты, значит, ваша скорость 167 м/мин.
На машине за 1 минуту, значит скорость 500 м/мин.

Чтобы перевести скорость из м/мин в м/сек, разделите скорость в м/мин на 60 (количество секунд в минуте).
Так, получается, что при ходьбе ваша скорость 100 м/мин / 60 = 1,67 м/сек.
Велосипед: 167 м/мин / 60 = 2,78 м/сек.
Машина: 500 м/мин / 60 = 8,33 м/сек.

Для перевода скорости из м/сек в км/ч – скорость в м/сек разделите на 1000 (количество метров в 1 километре) и полученное число умножьте на 3600 (количество секунд в 1 часе).
Таким образом, получается, что скорость ходьбы составляет 1,67 м/сек / 1000*3600 = 6 км/ч.
Велосипед: 2,78 м/сек / 1000*3600 = 10 км/ч.
Машина: 8,33 м/сек / 1000*3600 = 30 км/ч.
Для упрощения процедуры перевода скорости из м/сек в км/ч используйте коэффициент 3,6, который применяется следующим образом: скорость в м/сек*3,6=скорость в км/ч.
Ходьба: 1,67 м/сек*3,6 = 6 км/ч.
Велосипед: 2,78 м/сек*3,6 = 10 км/ч.
Машина: 8,33 м/сек*3,6= 30 км/ч.
Очевидно, что гораздо проще запомнить коэффициент 3,6, чем всю процедуру умножения-деления. В таком случае вы будете легко переводить скорость из одной величины в другую.

Видео по теме
Источники:
- как перевести м мин
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Движение тела под действием силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
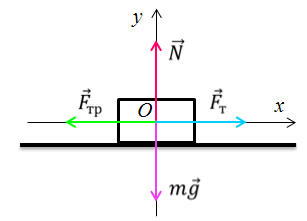
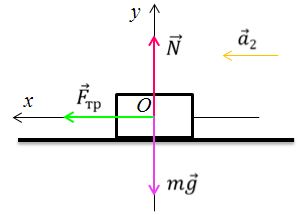
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ — тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline_ $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Так как сила трения $overline_ $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline_ right|$, то:
Но ускорение определяется также формулой:
где $v_ $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
Готовые работы на аналогичную тему
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
Так как $F_ =mu mg$, подставим в формулу (1) и получим:
Выразив из формулы (2) $v_ $найдем величину искомой скорости:
Ответ: Скорость автомобиля до выключения двигателя $v_ =20$ м/с.
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_ =20$м/с, $t=40$с.
Решение:
Уравнение движения сноубордиста будет иметь вид:
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
Так как сила трения $overline_ $равна $F_ =mu Bg$, находим коэффициент трения $mu $:
Ответ: $F_ =40H$, $mu =0,05$.
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Решение:
Уравнение движения тела:
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
Поскольку $F_ =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_ =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
Трение и движение по окружности
В этой статье собраны задачи, затрагивающие одновременно как тему “сила трения”, так и тему “движение по окружности”, придется вспомнить, что такое центробежная сила и как рассчитывается нормальное ускорение.
Задача 1. На горизонтальной дороге автомобиль делает поворот радиусом 16 м. Какова наибольшая скорость, которую может развить автомобиль, чтобы его не занесло, если коэффициент трения скольжения колес о дорогу равен 0,4? Во сколько раз изменится эта скорость зимой, когда коэффициент трения станет меньше в 4 раза?
Чтобы автомобиль не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Поэтому
Если коэффициент трения уменьшится вчетверо, скорость придется уменьшить вдвое: $upsilon_1=3,96$ м/с.
Ответ: $upsilon=7,9$ м/с, $upsilon_1=3,96$ м/с.
Задача 2. Горизонтально расположенный диск проигрывателя вращается с частотой 78 об/мин. На него поместили небольшой предмет. Расстояние от оси вращения до предмета составляет 7 см. На этом расстоянии предмет удерживается на диске. Каков коэффициент трения между предметом и диском?
Необходимо, чтобы сила трения была не меньше, чем центробежная сила. Поэтому
$$m omega^2 R =mu m g$$
$$4 pi^2 nu^2 R=mu g$$
Зная частоту вращения, определим коэффициент трения:
Задача 3. Определите, какого радиуса круг может описать велосипедист, если он едет со скоростью 25 км/ч, а предельный угол наклона велосипедиста к земле равен $60^$?
Чтобы велосипедиста не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Но колесо наклонено под углом $60^$, поэтому введем систему координат (ось $x$ – горизонтальна, ось $y$ – направлена вертикально вверх):
Теперь определим радиус из условия равенства силы трения и центробежной силы:
Задача 4. Описывая окружность радиусом 30 м, конькобежец наклонился в сторону поворота на угол $72^$ к горизонту. С какой скоростью двигался конькобежец? Каков коэффициент трения коньков о лед?
Введем систему координат и разложим силу реакции опоры на проекции на оси:
Как найти скорость через коэффициент трения
Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.
Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел.
Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.
Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Откуда берётся трение
Трение возникает по двум причинам:
- Все тела имеют шероховатости. Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
- Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Виды силы трения
В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.
- Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
- трение скольжения,
- трение покоя,
- трение качения.
- Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.
Сила трения покоя
Рассмотрим силу трения покоя подробнее.
Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.
Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Пока силы равны, холодильник остаётся на месте:
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя
Сила трения скольжения
Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности?
Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.
Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.
Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:
Как рассчитать и измерить силу трения
Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!
Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Сила реакции опоры обозначается N. Можно сделать вывод
Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.
Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.
Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
где μ — коэффициент трения, N — сила нормальной реакции опоры.
Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:
Сила трения качения
Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Причина трения качения — деформация катка и опорной поверхности. Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Направление силы трения
Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.
Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.
Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.
Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля сила трения покоя и вовсе направлена к центру окружности.
Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.
Подведём итоги
- Сила трения покоя меняется от нуля до максимального значения 0 < Fтр.покоя < Fтр.пок.макс в зависимости от внешнего воздействия.
- Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.макс
- Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N, где μ — коэффициент трения, N — сила нормальной реакции опоры.
- При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
- Коэффициент трения μ зависит от рода и степени обработки поверхностей 0 < μ < 1 .
- При одинаковых силе нормального давления и коэффициенте трения сила трения качения всегда меньше силы трения скольжения.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS72021 вы получите бесплатный доступ к курсу физики 7 класса, в котором изучается закон силы трения.
Задачи на силу трения
Проверьте, насколько хорошо вы разобрались в теме «Сила трения», — решите несколько задач. Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
- Однажды в день открытия железной дороги произошёл конфуз: угодливый чиновник, желая выслужиться перед Николаем I, приказал выкрасить рельсы белой масляной краской. Какая возникла проблема и как её удалось решить с помощью сажи?
- В один зимний день бабушка Нюра катала внука Алексея по заснеженной горизонтальной дороге. Чему равен коэффициент трения полозьев о снег, если сила трения, действующая на санки, равна 250 Н, а их масса вместе с Алексеем составляет 50 кг?
- На брусок массой m = 5 кг, находящийся на горизонтальной шероховатой поверхности μ = 0,7, начинает действовать сила F = 25 Н, направленная вдоль плоскости. Чему при этом равна сила трения, действующая на брусок?
Решения
- Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.
- Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g. Получаем формулу Fтр. = μ ⋅ m ⋅ g , откуда выразим искомую величину
Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .
- Прямолинейное равномерное движение на координатной прямой
- Уравнение прямолинейного равномерного движения
- Удобная система отсчета для решения задачи о прямолинейном движении
- График движения x=x(t)
- Как найти уравнение движения по графику движения?
- График скорости vx=vx(t)
- Как найти путь и перемещение по графику скорости?
- Задачи
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin{gather*} x=x_0+s=x_0+vt\ x=20+10t end{gather*}
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:
- если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)
В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) — координата в начальный момент времени, (v_x) — проекция вектора скорости движения.
Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:
- если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
 |
Построим графики зависимости координаты от времени для нашего примера:
x=20+10t — машина движется вправо (в направлении оси OX) |
п.5. Как найти уравнение движения по графику движения?
Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$
п.6. График скорости vx=vx(t)
В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с