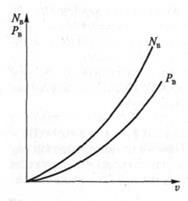
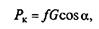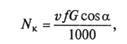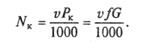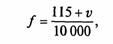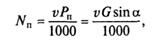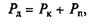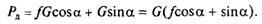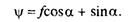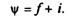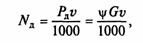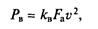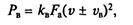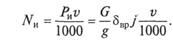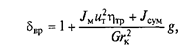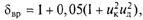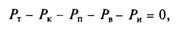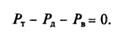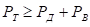Сопротивление — это сила, связанная с движущимся объектом в жидкой среде. Сила сопротивления определяется безразмерной величиной, называемой коэффициентом сопротивления, который помогает описать характер движения в жидкости.
Коэффициент аэродинамического сопротивления всегда определяет сопротивление подносится объекту, движущемуся в жидкости. Поскольку движущийся объект обладает определенной скоростью, коэффициент лобового сопротивления и скорость относятся к. Этот пост кратко объясняет взаимосвязь между коэффициентом лобового сопротивления и скоростью в различных аспектах.
Связь между коэффициентом лобового сопротивления и скоростью
Коэффициент аэродинамического сопротивления CD всегда определяется с использованием таких терминов, как плотность жидкости, опорная площадь поперечного сечения объекта, скорость и число Рейнольдса; таким образом, связь между коэффициентом лобового сопротивления и скоростью может быть записана с использованием уравнения.
CD=2FD/v2Ар
Где FD — сила сопротивления, ρ — массовая плотность жидкости; A — эталонная площадь, а v — относительная скорость объекта в жидкости.
Из приведенного выше выражения соотношение между коэффициентом лобового сопротивления CD и относительная скорость v задается как
CD∝ 1/об2
Вышеприведенное выражение означает что квадратное увеличение скорости уменьшает коэффициент лобового сопротивления. Таким образом, коэффициент лобового сопротивления и скорость обратно пропорциональны друг другу.
Соотношение силы сопротивления и скорости
Сила сопротивления всегда замедляет течение объекта в жидкости. По мере увеличения скорости пропорционально изменяется связанная с ней сила сопротивления. Сила сопротивления, действующая на объект в жидкости, определяется выражением
FD=1/2 СDv2Ар
Из приведенного выше уравнения в механике жидкости связь между сопротивлением и скоростью объясняется рассмотрением скорости объекта как низкой и высокой скорости. Сила сопротивления изменяется по-разному для низких и высоких скоростей.
Для низкоскоростного потока сила сопротивления пропорциональна скорости, определяемой выражением
FD∝ в
Для высокоскоростного потока сила сопротивления пропорциональна квадрату скорости, заданной как
FD∝ в2
Как скорость влияет на сопротивление?
Зависимость сопротивления от квадрата скорости вполне естественна в гидродинамике, поскольку скорость показывает некоторое отклонение сопротивления при изменении.
Объект, плавающий в жидкости, связан с удвоением скорости — это означает, что при увеличении скорости до квадратного значения сопротивление увеличивается в четыре раза. Четырехкратное увеличение сопротивления связано с другими объектами, связанными с сопротивлением. Влияние скорости на сопротивление определяется выражением
D∝ v2
Таким образом, мы можем записать вышеуказанную пропорциональность как
D=константа×v2
Константа в приведенном выше выражении рассматривается как плотность, площадь и коэффициент сопротивления, связанные с сопротивлением.
Таким образом, как относительная скорость увеличивается до своего квадратного значения, сопротивление увеличивается в четыре раза.
Сила сопротивления и угловая скорость
Угловая скорость всегда связано с вращательным движением объекта. Чтобы описать силу сопротивления с угловой скоростью, мы должны рассмотреть выражение линейного сопротивления; он приведен ниже:
FD=1/2 СDv2Ар
Однако мы говорим о вращательное движение, крутящий момент относительно силы сопротивления, заданной как
τ ∝ автодом2Ар
Поскольку движение является вращательным, угловая скорость объекта может быть связана с линейной скоростью как
v=ω×r, где r — радиус пути вращения, а ω — угловая скорость, связанная с вращающимся объектом.
Подставляя значение v, получаем
τ ∝ р3 ω2Ар
Из приведенного выше выражения сопротивление сила эквивалентна крутящему моменту действует на вращающийся объект.
Таким образом, сила сопротивления может быть записана как
FD=1/2 СDr3 ω2Ар
Сила сопротивления и конечная скорость
Когда объект свободно падает из жидкости, максимальная скорость, приобретаемая объектом, называется конечной скоростью.
Рассмотрим пример парашютиста; когда он ныряет, он падает под действием силы тяжести. На водолаза действуют две силы: сила тяжести и сила сопротивления. Однако по мере увеличения скорости ныряльщика увеличивается и величина силы сопротивления, пока она не станет равной величина гравитационной силы.
Когда величина сопротивления и гравитационной силы становятся равными, результирующая сила, действующая на дайвера, сводится к нулю, что делает ускорение также равным нулю. В этот момент дайвер достиг постоянная скорость называется конечной скоростью.
Связь между силой сопротивления и конечной скоростью
В предыдущем разделе мы обсудили связь между коэффициентом сопротивления и скоростью, силой сопротивления и угловой скоростью. Точно так же отношения между сила сопротивления и конечная скорость можно получить, рассматривая падающий предмет.
Как известно, когда объект достигает предельной скорости, на него действуют две силы: сила сопротивления и гравитационная сила. Силу гравитации можно определить как вес объекта. Таким образом, чистая сила определяется выражением
Fсеть=ВФD, где W=мг
Когда объект достигает предельной скорости, результирующая сила Fсеть=ма=0
Таким образом, FD=W=мг
Подставляя вышеприведенное уравнение, получаем
FD=1/2 СDVT2 Ар
мг=1/2 СDVT2 Ар
Переставляя члены, мы получаем конечную скорость как
vT2=2мг/КлDАр
vT=√2мг/КDАр
Что такое сила сопротивления?
На движущийся объект всегда действует сила препятствия, оказывающая сопротивление движению.
Сила сопротивления действует на движущийся объект в жидкости (жидкости или газе). Его можно определить как силу, действующую на твердое тело, движущееся в жидкости, противоположную относительному движению жидкости.
Решенные задачи по силе сопротивления, коэффициенту сопротивления и скорости
Сила сопротивления, действующая на тело, равна 235 Н, плотность равна 1.11 кг/м.3, а площадь поперечного сечения кузова 2.33м2. Коэффициент сопротивления тела рассчитывается как 0.14, следовательно, рассчитывается скорость тела.
Решение:
Сила сопротивления FD= 235N
Плотность ρ=1.11 кг/м3.
Поперечное сечение А = 2.33 м2
Коэффициент аэродинамического сопротивления CD= 0.14
Скорость тела
v=√2FD/CD Ар
v= √2(235)/(0.14) * 1.11 Ар
v=36.02 м/с.
Вычислите силу сопротивления тела, вращающегося по окружности радиусом 3 м в воздухе со скоростью 12 м/с. Площадь поперечного сечения 3.4м2, а коэффициент аэродинамического сопротивления равен 0.55.
Решение:
Коэффициент аэродинамического сопротивления CD= 0.55
Радиус пути r=3м
Площадь поперечного сечения A=3.4 м2
Угловая скорость ω=12 м/с
Плотность воздуха ρ=1.21 кг/м3
FD=1/2 СDr3 ω2Ар
FD=1/2 * 0.55 * 33 * 122* 3.4* 1.21
FD= 4.3 × 103N
Водолаз массой 79 кг ныряет с парашютом. Коэффициент аэродинамического сопротивления водолаза принимается равным 0.73, а площадь поперечного сечения считается равной 0.17 м.2. Вычислите конечную скорость дайвера.
Решение:
Дано – масса водолаза m=79кг
Коэффициент аэродинамического сопротивления CD= 0.73
Площадь поперечного сечения А=0.17 м2
Из приведенных выше данных конечная скорость может быть определена как
vT=√2мг/КD Ар
Плотность воздуха ρ=1.21 кг/м3
Ускорение свободного падения g=9.8 м/с2
vT=√2(79*9.8)/0.73*0.17*1.21
vT=101.600 м/с.
При движении на тело действуют различные силы. Решая задачу-модель, зачастую пренебрегают силами сопротивления, в простых случаях рассматривают линейную зависимость силы сопротивления от параметров. В реальной жизни закон зависимости силы сопротивления от параметров среды имеет более сложный вид. Решение задач на сопротивление, безусловно, приблизит нас к более точному описанию явления.
1) Два тела одинакового объема V соединены длинной нитью. Плотность первого тела ρ1, плотность второго тела ρ2. Систему сбрасывают с зависшего воздушного шара. Через некоторое время скорость падения системы становится постоянной, так как сила тяжести уравновешивается силой сопротивления воздуха. Найдите силу натяжения нити в установившемся режиме падения. [решение]
2) Из (А) в (Б) можно добраться только на моторной лодке по узкой реке, скорость течения которой всюду одинакова. Лодке с одним подвесным мотором на путь из A в Б требуется время t1 = 50 минут, а с двумя моторами — время t2 = t1/2. Сила тяги двух моторов вдвое больше силы тяги одного. За какое минимальное время можно добраться из Б в А на лодке с одним и с двумя моторами? Известно, что сила сопротивления движению лодки пропорциональна квадрату скорости движения относительно воды. [решение]
3) Деревянный шарик, опущенный под воду, всплывает в установившемся режиме со скоростью v1, а точно такой же по размеру пластмассовый тонет со скоростью v2. Куда и с какой скоростью будут двигаться в воде эти шарики, если их соединить ниткой? Сила сопротивления пропорциональна скорости. Гидродинамическим взаимодействием шариков можно пренебречь. Считайте, что на движущийся шарик действует такая же сила Архимеда, как и на покоящийся. [решение]
4) Школьник заметил, что сферический пузырёк воздуха диаметром d1 = 1 мм всплывает в жидкости плотностью ρж = 1 г/см3 со скоростью v1 = 0,5 см/с. Пузырёк диаметром d2 = 2 мм всплывает со скоростью v2 = 2 см/с, а сферическая металлическая дробинка такого же диаметра плотностью ρ = 5 г/см3 тонет со скоростью v3 = 8 см/с. С какой скоростью будет всплывать в этой жидкости пластмассовый шарик плотностью ρ = (2/3) г/см3 и диаметром d = 3 мм? Считайте, что характер зависимости сил сопротивления движению от скорости и диаметра шарика — степенной, и для всех указанных тел одинаков. [решение]
5) Шарик массой m и объёмом V под действием силы тяжести падает в жидкости плотностью ρ с постоянной скоростью v. Сила сопротивления жидкости движению шарика пропорциональна квадрату скорости. К шарику прилагается дополнительно горизонтально направленная сила f. Какой станет вертикальная составляющая скорости шарика v1? [решение]
6) В неоднородной вязкой среде (см. рис.) сила сопротивления, действующая на тело массой m, пропорциональна квадрату скорости, причём коэффициент пропорциональности α зависит от координаты тела x в направлении движения (то есть выражение для силы сопротивления имеет вид f = −α(x)v). Какой должна быть зависимость α(x), чтобы при любой начальной скорости, направленной вдоль оси x, тело, пущенное из точки x = 0, двигалось в данной среде равнозамедленно? Силу тяжести не учитывайте. [решение]
7) Лодку массой m, стоящую в спокойной воде, толкнули со скоростью vo. Какой путь пройдет она до того, как остановится, если сила сопротивления движению пропорциональна скорости: F = αv? [решение]
Вы читате материалы из пособия для подготовки к олимпиадам по физике. Далее: задачи на минимум и максимум.
Лекция 7. Уравнение движения автомобиля
План лекции
7.1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление
7. 2. Уравнение движения автомобиля
7. 1 Силы сопротивления движению и мощности, затрачиваемые на их преодоление
Силами сопротивления называются силы, препятствующие Движению автомобиля. Эти силы направлены против его движения.
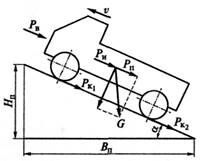
При движении на подъеме, характеризуемом высотой Нп, длиной проекции Вп на горизонтальную плоскость и углом подъема дороги а, на автомобиль действуют следующие силы сопротивления (рис. 7.1): сила сопротивления качению Рк, равная сумме сил сопротивления качению передних (РК1) и задних (РК2) колес, сила сопротивления подъему Рп, сила сопротивления воздуха Рв и сила сопротивления разгону Ри. Силы сопротивления качению и подъему связаны с особенностями дороги. Сумма этих сил называется силой сопротивления дороги Рд.
Рис. 7.1. Силы сопротивления движению автомобиля
Сила сопротивления качению
Возникновение силы сопротивления качению при движении обусловлено потерями энергии на внутреннее трение в шинах, поверхностное трение шин о дорогу и образование колеи (на деформируемых дорогах).
Рекомендуемые материалы
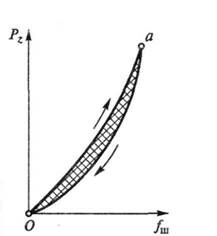
О потерях энергии на внутреннее трение в шине можно судить по рис. 7.2, на котором приведена зависимость между вертикальной нагрузкой на колесо и деформацией шины — ее прогибом fш.
При движении колеса по неровной поверхности шина, испытывая действие переменной нагрузки, деформируется. Линия Оа, которая соответствует возрастанию нагрузки, деформирующей шину, не совпадает с линией аО, отвечающей снятию нагрузки. Площадь области, заключенной между указанными кривыми, характеризует потери энергии на внутреннее трение между отдельными частями шины (протектор, каркас, слои корда и др.).
Потери энергии на трение в шине называются гистерезисом, а линия ОаО — петлей гистерезиса.
Потери на трение в шине необратимы, так как при деформации она нагревается и из нее выделяется теплота, которая рассеивается в окружающую среду. Энергия, затрачиваемая на деформацию шины, не возвращается полностью при последующем восстановлении ее формы.
Сила сопротивления качению Рк достигает наибольшего значения при движении по горизонтальной дороге. В этом случае
Рк =fG, где G — вес автомобиля, Н; f — коэффициент сопротивления качению.
Рис. 7.2. Потери энергии на внутреннее трение в шине:
а — точка, соответствующая максимальным значениям нагрузки и прогиба шины
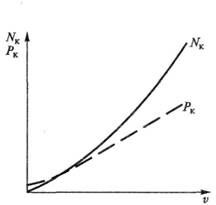
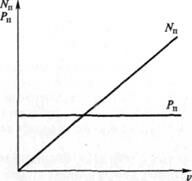
Рис. 7.3. Зависимости силы сопротивления качению Рк и мощности NK, необходимой для преодоления этого сопротивления, от скорости автомобиля
При движении на подъеме и спуске сила сопротивления качению уменьшается по сравнению с Рк на горизонтальной дороге, и тем значительнее, чем они круче. Для этого случая движения сила сопротивления качению
где а — угол подъема, °.
Зная силу сопротивления качению, можно определить мощность, кВт, затрачиваемую на преодоление этого сопротивления:
где v — скорость автомобиля, м/с. Для горизонтальной дороги cos 0° = 1 и
Зависимости силы сопротивления качению Рк и мощности NK от скорости автомобиля v показаны на рис. 7.3.
Коэффициент сопротивления качению
Коэффициент сопротивления качению существенно влияет на потери энергии при движении автомобиля. Он зависит от многих конструктивных и эксплуатационных факторов и определяется экспериментально. Его средние значения для различных дорог при Нормальном давлении воздуха в шине составляют 0,01 …0,1.
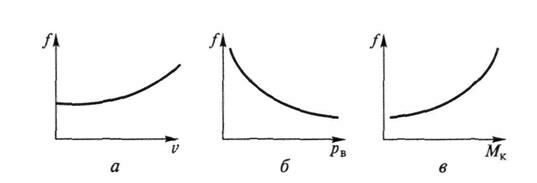
Рис 7.4. Зависимости коэффициента сопротивления качению от
скорости движения (а), давления воздуха в шине (б) и момента,
передаваемого через колесо (в)
Рассмотрим влияние различных факторов на коэффициент сопротивления качению.
Скорость движения. При изменении скорости движения в интервале 0…50 км/ч коэффициент сопротивления качению изменяется незначительно и его можно считать постоянным в указанном диапазоне скоростей.
При повышении скорости движения за пределами указанного интервала коэффициент сопротивления качению существенно увеличивается (рис. 7.4, а) вследствие возрастания потерь энергии в шине на трение.
Коэффициент сопротивления качению в зависимости от скорости движения можно приближенно рассчитать по формуле
где v — скорость автомобиля, км/ч.
Тип и состояние покрытия дороги. На дорогах с твердым покрытием сопротивление качению обусловлено главным образом деформациями шины.
При увеличении числа дорожных неровностей коэффициент сопротивления качению возрастает.
На деформируемых дорогах коэффициент сопротивления качению определяется деформациями шины и дороги. В этом случае он зависит не только от типа шины, но и от глубины образующейся колеи и состояния грунта.
Значения коэффициента сопротивления качению при рекомендуемых уровнях давления воздуха и нагрузки на шину и средней скорости движения на различных дорогах приведены ниже:
Асфальто- и цементобетонное шоссе:
в хорошем состоянии…………………………… 0,007…0,015
в удовлетворительном состоянии………….. 0,015…0,02
Гравийная дорога в хорошем состоянии….. 0,02…0,025
Булыжная дорога в хорошем состоянии…… 0,025…0,03
Грунтовая дорога сухая, укатанная………….. 0,025…0,03
Песок……………………………………………………… 0,1…0,3
Обледенелая дорога, лед…………………………. 0,015…0,03
Укатанная снежная дорога………………………. 0,03…0,05
Тип шины. Коэффициент сопротивления качению во многом зависит от рисунка протектора, его износа, конструкции каркаса и качества материала шины. Изношенность протектора, уменьшение числа слоев корда и улучшение качества материала приводят к падению коэффициента сопротивления качению вследствие снижения потерь энергии в шине.
Давление воздуха в шине. На дорогах с твердым покрытием при уменьшении давления воздуха в шине коэффициент сопротивления качению повышается (рис. 7.4, б). На деформируемых дорогах при снижении давления воздуха в шине уменьшается глубина колеи, но возрастают потери на внутреннее трение в шине. Поэтому для каждого типа дороги рекомендуется определенное давление воздуха в шине, при котором коэффициент сопротивления качению имеет минимальное значение.
Нагрузка на колесо. При увеличении вертикальной нагрузки на колесо коэффициент сопротивления качению существенно возрастает на деформируемых дорогах и незначительно — на дорогах с твердым покрытием.
Момент, передаваемый через колесо. При передаче момента через колесо коэффициент сопротивления качению возрастает (рис. 7.4, в) вследствие потерь на проскальзывание шины в месте ее контакта с дорогой. Для ведущих колес значение коэффициента сопротивления качению на 10… 15 % больше, чем для ведомых.
Коэффициент сопротивления качению оказывает существенное влияние на расход топлива и, следовательно, на топливную экономичность автомобиля. Исследования показали, что даже небольшое уменьшение этого коэффициента обеспечивает ощутимую экономию топлива. Поэтому неслучайно стремление конструкторов и исследователей создать такие шины, при использовании которых коэффициент сопротивления качению будет незначительным, но это весьма сложная проблема.
Сила сопротивления подъему
Вес автомобиля, который движется на подъеме, можно разложить на две составляющие (см. рис. 7.1): параллельную и перпендикулярную поверхности дороги. Составляющая силы тяжести, параллельная поверхности дороги, представляет собой силу сопротивления подъему, Н:
Рп = Gsinα,
где G — вес автомобиля, Н; a — угол подъема, °.
Рис. 7.5. Зависимости силы сопротивления подъему Рп и мощности Nп, необходимой для его преодоления, от скорости автомобиля
В качестве характеристики крутизны подъема наряду с углом α используют величину i, называемую уклоном и равную i = H/Bn, где Нп — высота подъема; Bn — длина его проекции на горизонтальную плоскость. Сила сопротивления подъему может быть направлена как в сторону движения, так и против него. В процессе подъема она действует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направленная в сторону движения, становится движущей.
Зная силу сопротивления подъему, можно определить мощность, кВт, необходимую для преодоления этого сопротивления:
где v — скорость автомобиля, м/с.
Зависимости силы сопротивления подъему Рп „ и мощности Nn, необходимой для преодоления этого сопротивления, от скорости автомобиля v приведены на рис. 7.5.
Сила сопротивления дороги
Сила сопротивления дороги представляет собой сумму сил сопротивления качению и сопротивления подъему:
или
Выражение в скобках, характеризующее дорогу в общем случае, называется коэффициентом сопротивления дороги:
При малых углах подъема (не превышающих 5°), характерных для большинства автомобильных дорог с твердым покрытием, коэффициент сопротивления дороги
Сила сопротивления дороги в этом случае
Рд =ψG
Зная силу сопротивления дороги, можно определить мощность, кВт, необходимую для его преодоления:
где скорость автомобиля v выражена в м/с, вес G — в Н, мощность NД — в кВт.
Зависимости силы сопротивления дороги Рв и мощности NД, затрачиваемой на его преодоление, от скорости автомобиля v представлены на рис. 7.6.
Сила сопротивления воздуха
При движении действие силы сопротивления воздуха обусловлено перемещением частиц воздуха и их трением о поверхность автомобиля. Если он движется при отсутствии ветра, то сила сопротивления воздуха, Н:
тогда как при наличии ветра
где 
kв — коэффициент сопротивления воздуха (коэффициент обтекаемости), Н-с2/м4; Fa — лобовая площадь автомобиля, м2; v — скорость автомобиля, м/с; vB — скорость ветра, м/с (знак «+» соответствует встречному ветру, знак «-» — попутному).
Коэффициент сопротивления воздуха, зависящий от формы и качества поверхности автомобиля, определяется экспериментально при продувке в аэродинамической трубе.
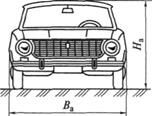
Рис. 7.7. Площади лобового сопротивления легкового (а) и грузового
(б) автомобилей
Коэффициент сопротивления воздуха, Н-с2/м4, составляет 0,2…0,35 для легковых автомобилей, 0,35…0,4 — для автобусов и 0,6…0,7 — для грузовых автомобилей. При наличии прицепов сопротивление воздуха увеличивается, так как возрастает наружная поверхность трения и возникают завихрения воздуха между тягачом и прицепами. При этом каждый прицеп вызывает увеличение коэффициента kв в среднем на 15…25 %.
Лобовая площадь автомобиля зависит от его типа (рис. 7.7). Ее приближенное значение, м2, можно вычислить по следующим формулам:
FA = ВНа — для грузовых автомобилей и автобусов;
Fa = 0,78ВаНа — для легковых автомобилей,
где В — колея колес автомобиля, м; На — наибольшая высота автомобиля, м; Bа — наибольшая ширина автомобиля, м.
Мощность, кВт, затрачиваемая на преодоление сопротивления воздуха:
— при отсутствии ветра;
— при наличии ветра.
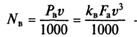
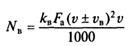
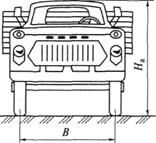
Зависимости силы сопротивления воздуха Рв и мощности NB, необходимой для преодоления этого сопротивления, от скорости автомобиля v приведены на рис. 7.8.
Рис. 7.8. Зависимости силы сопротивления воздуха Рв и мощности Nb, необходимой для преодоления этого сопротивления, от скорости автомобиля
Сила сопротивления разгону
Сила сопротивления разгону возникает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.
Сила сопротивления разгону, Н:
=
где G — вес автомобиля, Н; g — ускорение силы тяжести, м/с2;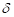 
вр — коэффициент учета вращающихся масс автомобиля; j — ускорение автомобиля, м/с2.
Мощность, кВт, затрачиваемая на разгон:
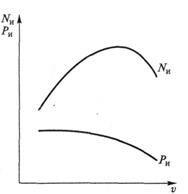
Зависимости силы сопротивления разгону Ри и мощности NK, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 7.9.
Рис. 7.9. Зависимости силы сопротивления разгону Ря и мощности /Уи, необходимой для преодоления этого сопротивления, от скорости автомобиля
Коэффициент учета вращающихся масс
Этот коэффициент учитывает дополнительное сопротивление разгону автомобиля, вызванное раскручиванием вращающихся частей двигателя, трансмиссии и колес.
Коэффициент учета вращающихся масс показывает, во сколько раз мощность, затрачиваемая на разгон автомобиля, больше мощности, необходимой для установившегося движения:
где JM — момент инерции маховика; uТ,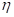 
Чтр — передаточное число и КПД трансмиссии; Jсум — суммарный момент инерции всех колес автомобиля.
Коэффициент учета вращающихся масс для автомобиля с полной нагрузкой можно приближенно рассчитать по формуле
где ик, ид — передаточные числа основной и дополнительной коробок передач.
7.2. Уравнение движения автомобиля
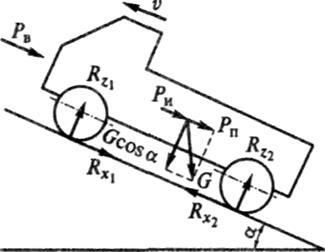
Для вывода уравнения движения рассмотрим разгон автомобиля на подъеме (рис. 7.10).
Спроецируем все силы, действующие на автомобиль, на поверхность дороги:
(7.1)
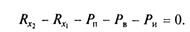
Подставим в формулу (7.1) касательные реакции дороги RX1 и RX2, объединим члены с коэффициентом сопротивления качению f и члены с ускорением j и, принимая во внимание соотношения f(RZl + RZ2)- Pk и /*, + Л2 = Jк , а также коэффициент учета вращающихся масс, получим уравнение движения автомобиля в общем виде:
или
(7.2)
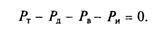
Уравнение движения автомобиля выражает связь между движущими силами и силами сопротивления движению. Оно позволяет определить режим движения автомобиля в любой момент.
Так, например, при установившемся (равномерном) движении
Из уравнения (7.2) следует, что безостановочное движение автомобиля возможно только при условии
Ещё посмотрите лекцию «18 Дизайн молекул лекарств» по этой теме.
Рис. 7.10. Схема сил, действующих на автомобиль на подъеме
данное неравенство связывает конструктивные параметры автомобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Однако оно не гарантирует отсутствия буксования ведущих колес. Безостановочное движение автомобиля без буксования ведущих колес возможно лишь при соблюдении условия
Рсц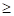 
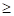
РТ РД + РВ.
Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде
Рсц 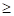РТ = РД + РВ
Загрузить PDF
Загрузить PDF
Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.
-
1
Формула для нахождения предельной скорости: v = квадратный корень из ((2*m*g)/(ρ*A*C)). Подставьте значения переменных для нахождения предельной скорости v.
- m = масса падающего тела.
- g = ускорение свободного падения. На Земле оно примерно равно 9,8 м/с2.
- ρ = плотность жидкости, в которой падает тело.
- A= площадь проекции тела. Это площадь области тела, перпендикулярная направлению движения тела.
- C = коэффициент лобового сопротивления. Он зависит от формы тела. Чем более обтекаемая форма, тем ниже коэффициент.
Реклама
-
1
Найдите массу падающего тела. В метрической системе ее измеряют в граммах или килограммах.
-
2
Задайте ускорение свободного падения. На расстоянии, достаточно близком к земле, чтобы столкнуться с сопротивлением воздуха, эта величина равна 9,8 м/с2.
-
3
Вычислите силу тяжести. Она равна массе тела умноженной на ускорение свободного падения F = m*g.
Реклама
-
1
Найдите плотность среды. Для тела, падающего сквозь атмосферу Земли, плотность будет меняться в зависимости от высоты и температуры воздуха. Это делает вычисления предельной скорости свободно падающего тела особенно сложным, так как плотность воздуха меняется по мере того, как тело приближается к земле. Тем не менее, вы можете найти приблизительные значения плотности воздуха в учебниках или в других источниках.
- В качестве ориентира, плотность воздуха на уровне моря при температуре 15°C равна 1,225 кг/м3.
-
2
Оцените коэффициент аэродинамического сопротивления тела. Это число зависит от обтекаемости тела. К сожалению, это очень сложная для вычисления величина, которая включает в себя принятие определенных научных предположений. Не пытайтесь вычислить коэффициент аэродинамического сопротивления без помощи аэродинамической трубы и некоторых сложных аэродинамических вычислений. Вместо этого возьмите готовое значение для тела, по форме похожее на ваше.
-
3
Вычислите площадь проекции объекта. Последней переменной, которую вы должны найти, является площадь поперечного сечения тела. Представьте себе силуэт падающего тела, посмотрев на него сверху. Площадь этого силуэта (площадь проекции), который проецируется на плоскость, и надо найти. Опять же, это трудное для вычисления значение, за исключением простых по форме тел.
-
4
Найдите силу сопротивления, которая противоположна силе тяжести. Если вы знаете скорость тела, то сила сопротивления находится по формуле: (C*ρ*A*(v^2))/2.
Реклама
Советы
- Падая без парашюта, человек ударяется о землю со скоростью равной примерно 240 км/ч.
- Предельная скорость на самом деле немного меняется во время свободного падения. Сила тяжести увеличивается по мере приближения тела к центру Земли, но этим можно пренебречь. Плотность среды растет с уменьшением высоты падения. Это гораздо более заметный эффект. Парашютист по мере падения на самом деле будет замедляться, так как плотность атмосферы сильно увеличивается с уменьшением расстояния до Земли.
Реклама
Об этой статье
Эту страницу просматривали 37 463 раза.
Была ли эта статья полезной?
Время на прочтение
3 мин
Количество просмотров 9.7K
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. — это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности — Ватт:
Перейдем к основной части, а именно — к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг — масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше — измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
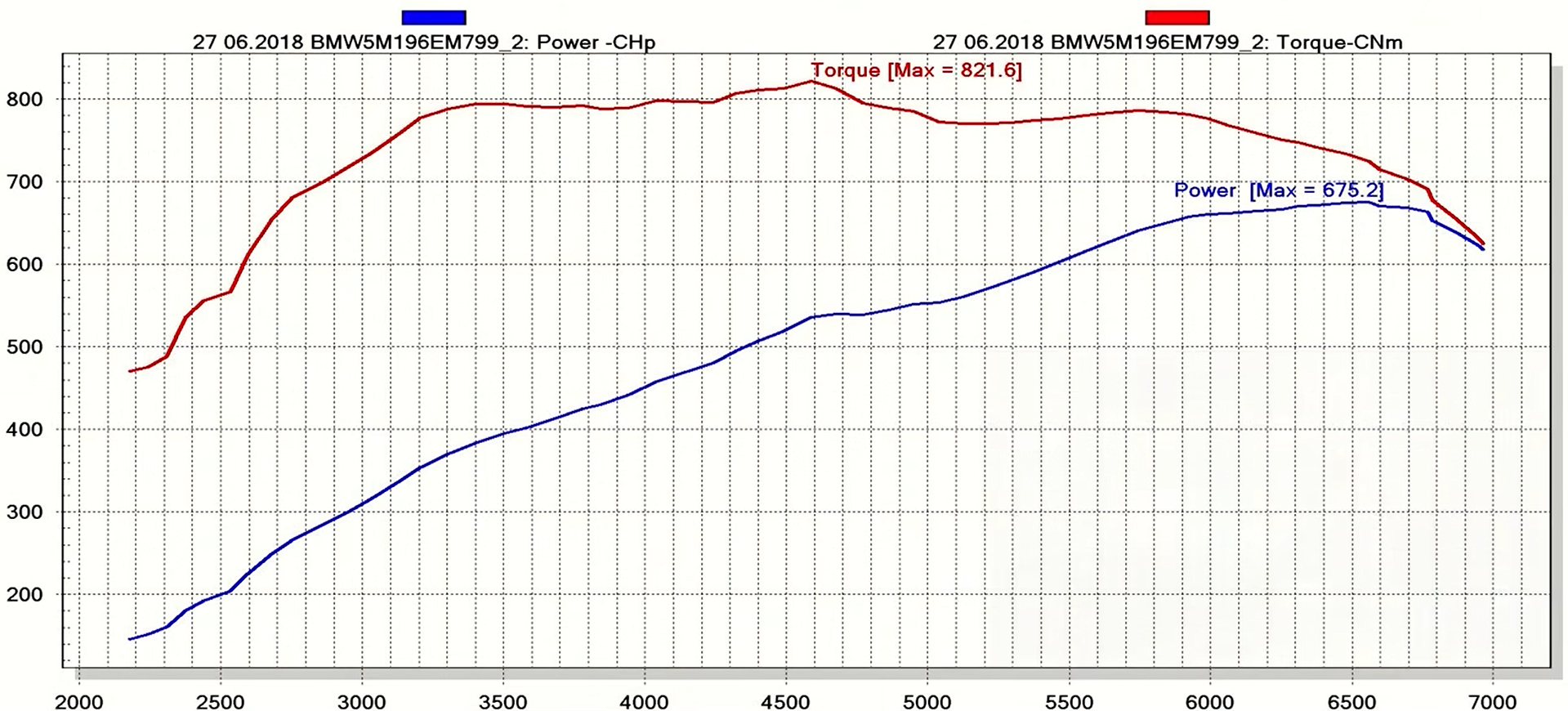
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.
Главное, что мы должны усвоить из этого графика — мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
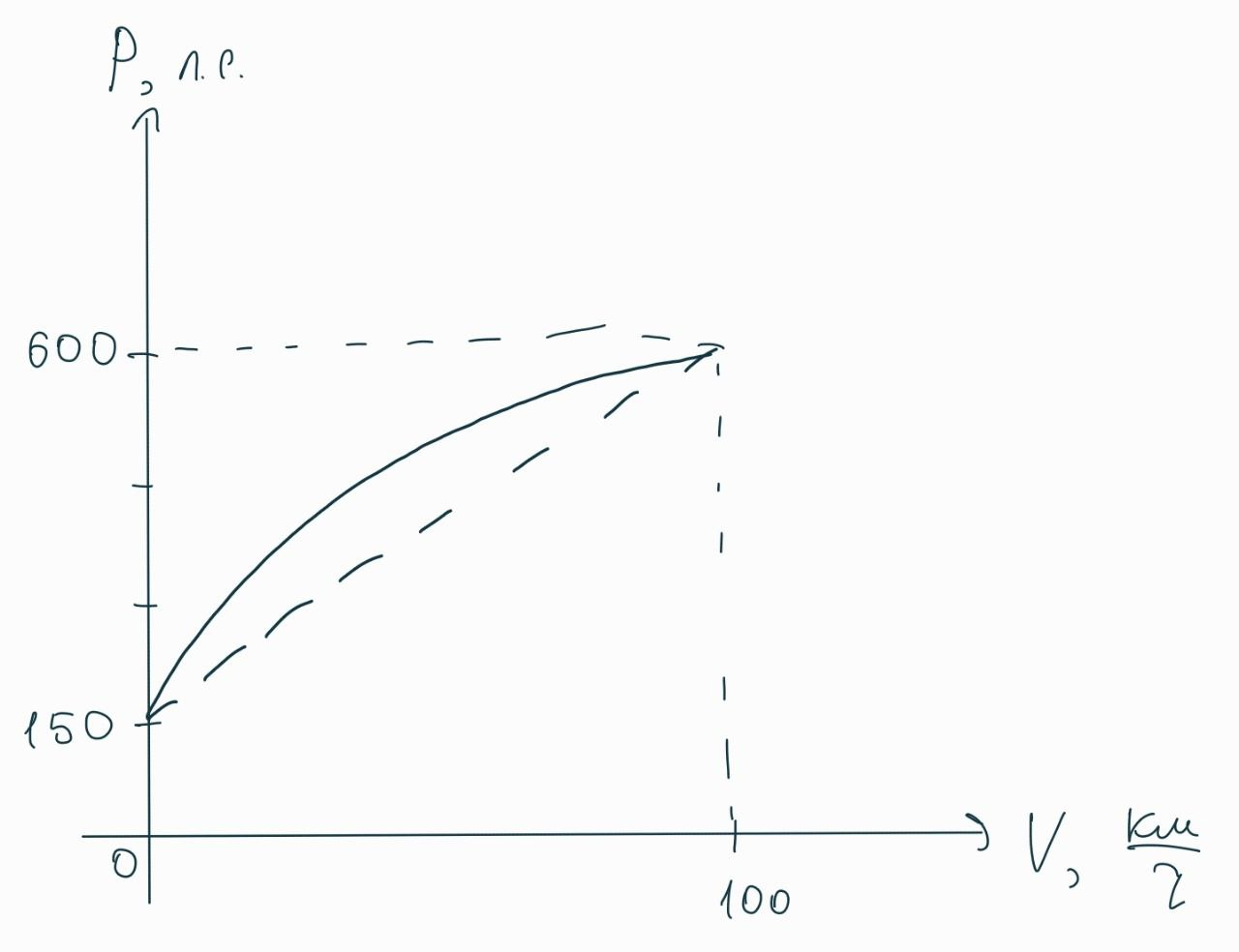
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную — 600 л.с. (7000 об/мин):
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к «паспортным» 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
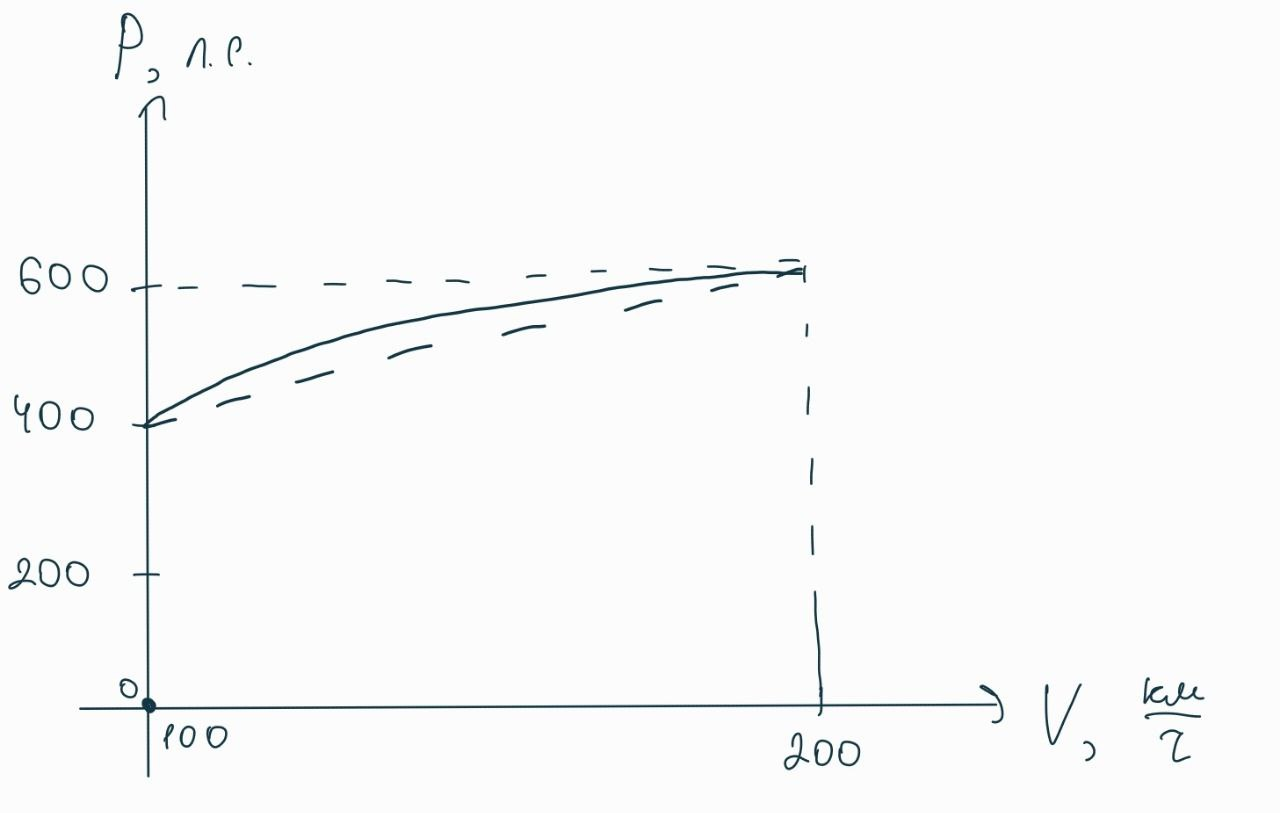
Так делать конечно же нельзя! После 2-й передачи двигатель работает на «комфортных» для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
![t = dfrac{m (V^2 - V_0^2)}{2P} = dfrac{2 cdot 10^3 text{ кг}cdot left[left(56 dfrac{м}{с} right)^2 - left(28 dfrac{м}{с} right)^2 right]}{2cdot 300 cdot 10^3 text{ Вт}} simeq 7.8 text{ с}](https://habrastorage.org/getpro/habr/upload_files/6d8/4d4/6ae/6d84d46ae2709c0005f27dea37f6fecc.svg)
Время разгона «по паспорту» 7.6 с. И снова мы оказались близко к истине!
P.S. не хочу объяснять, откуда взялось (V^2 — V_0^2), можете повыводить на досуге 
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная «школьные» формулы по физике, можно решать такие интересные задачки, связанные с жизнью.