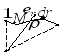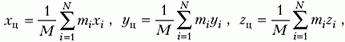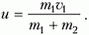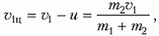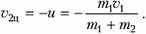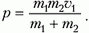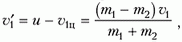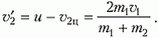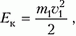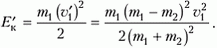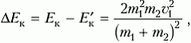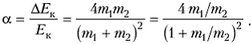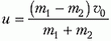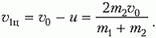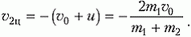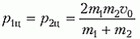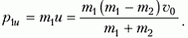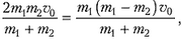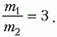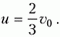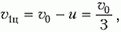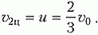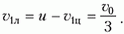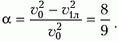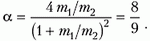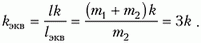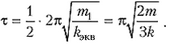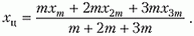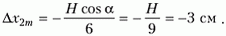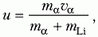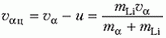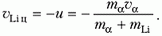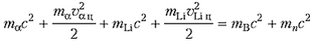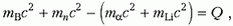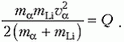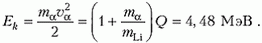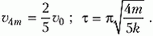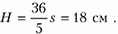Определение центра масс, теория и онлайн калькуляторы
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
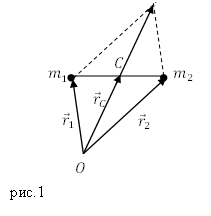
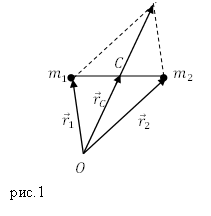
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${overline{r}}_1 и {overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${overline{r}}_C$ (рис.1).
Из рис.1 видно, что:
[{overline{r}}_C=frac{{overline{r}}_1+ {overline{r}}_2}{2}left(1right).]
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
[{overline{r}}_C=frac{{overline{r}}_1m_1+ {overline{r}}_2m_2}{m_1+m_2}left(2right).]
Радиус -вектор ${overline{r}}_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц ${overline{r}}_1$ и ${overline{r}}_2$. Это становится очевидным, если формулу (2) представить в виде:
[{overline{r}}_C=frac{m_1}{m_1+m_2}{overline{r}}_1+frac{m_2}{m_1+m_2}{overline{r}}_2left(3right).]
Выражение (3) показывает, что радиус-вектор каждой частицы входит в ${overline{r}}_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
[{overline{r}}_c=frac{sumlimits^N_{i=1}{m_i{overline{r}}_i}}{sumlimits^N_{i=1}{m_i}}left(4right).]
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
[x_c=frac{sumlimits^N_{i=1}{m_ix_i}}{sumlimits^N_{i=1}{m_i}}left(5right).]
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
[y_c=frac{sumlimits^N_{i=1}{m_iy_i}}{sumlimits^N_{i=1}{m_i}}left(6right).]
[z_c=frac{sumlimits^N_{i=1}{m_iz_i}}{sumlimits^N_{i=1}{m_i}}left(7right).]
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс (${overline{v}}_c=frac{d{overline{r}}_c}{dt}$) запишем как:
[{overline{v}}_c=frac{m_1{overline{v}}_1+m_2{overline{v}}_2+dots +m_n{overline{v}}_n}{m_1+m_2+dots +m_n}=frac{overline{P}}{M}left(8right),]
где $overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Пример 2
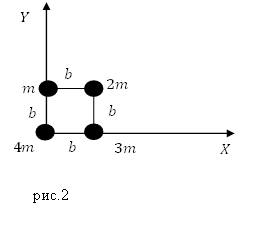
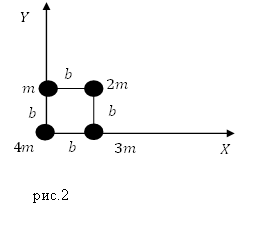
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
[left{ begin{array}{c}
x_c=frac{sumlimits_i{Delta m_ix_i}}{m};; \
y_с=frac{sumlimits_i{Delta m_iy_i}}{m}. end{array}
right.]
Вычислим массу рассматриваемой системы точек:
[m=m+2m+3m+4m=10 m.]
Тогда абсцисса центра масс $x_{c } $равна:
[x_c=frac{0cdot 4m+3mcdot b+2mcdot b}{10m}=0,5 b.]
Ордината $y_с$:
[y_с=frac{0cdot m+mcdot b+2mcdot b}{10m}=0,3 b.]
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Пример 2
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
[frac{s_1}{s_2}=frac{m_2}{m_1}left(2.1right).]
По условию:
[s=s_1+s_2left(2.2right).]
Из уравнений (2.1) и (2.2) получаем:
[s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}.]
Ответ. $s_1=sfrac{m_2}{m_1+m_2};; s_2=sfrac{m_1}{m_1+m_2}$
Читать дальше: период и частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
В
любой системе частиц можно найти точку,
называемую центром масс
,
которая обладает рядом важных свойств.
Её положение относительно начала данной
системы отчета, определяется
радиусом-вектором
.
Центр
масс совпадает с центром тяжести для
однородного поля сил тяготения.
Найдем
скорость движения центра масс системы
;
Если
,
то система, как целое, покоится, т.е.
имеет смысл скорости движения всей
системы, как целого. Поскольку,
,
то
т.е., импульс
системы равен произведению ее массы на
скорость движения центра масс.
3.4. Уравнение движения центра масс.
Основной
закон динамики
можно записать в иной форме, зная понятие
центра масс системы:
Это
есть уравнение
движения центра масс системы,
одно из важнейших уравнений механики.
Оно утверждает, что центр
масс любой системы частиц движется так,
как если бы вся масса системы была
сосредоточена в этой точке и к ней были
бы приложены все внешние силы.
Ускорение
центра масс системы совершенно не
зависит от точек приложения внешних
сил.
Если
,
то
,
значит
и
— это случай замкнутой системы в
инерциальной системе отсчета. Таким
образом, если центр масс системы движется
равномерно и прямолинейно, это означает,
что её импульс сохраняется в процессе
движения.
Пример:
однородный цилиндр массы
и радиуса
скатывается без скольжения по наклонной
плоскости, составляющей угол
с горизонтом. Найти уравнение движения?
Совместное
решение дает значение параметров
Уравнение движения
центра масс
совпадает
с основным уравнением динамики
материальной точки и является его
обобщением на систему частиц: ускорение
системы как целого пропорционально
результирующей всех внешних сил и
обратно пропорционально массе системы.
Систему
отсчета, жестко связанную с центром
масс, которая движется поступательно
относительно ИСО называют системой
центра масс. Ее особенностью является
то, что полный импульс системы частиц
в ней всегда равен нулю, так, как
.
4.Работа и энергия
4.1 Работа
П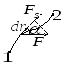
частица М под действием силы
совершает перемещение по некоторой
траектории 1-2. Сила, в общем случае, может
меняться во времени по модулю и
направлению, но на элементарном
перемещении
её можно считать
.
Действие
силы на перемещении
характеризуется физической величиной,
равной скалярному произведению
,
которая называется элементарной
работой силы
на перемещении
.
Её можно записать как
,
где
— угол между
и
— элементарный путь
проекция вектора
на вектор
,
или на направление s.
З
начит, элементарная работа
(*)
—
величина алгебраическая, она может быть
,
или
,
а также равна нулю при
.
Суммируя
элементарные работы (т.е., интегрируя )
по всем элементарным участкам пути от
1 к 2 найдем работу силы
на данном пути.
.
Геометрический
смысл этого выражения виден из рисунка,
на котором
—
площадь полоски шириной
и высотой
;
—
площадь под всей кривой. Над осью работа
силы положительна, под осью — отрицательна.
Размерность
работы
.
Найдем
для примера работу некоторых центральных
сил.
1.
Работа гравитационной или кулоновской
силы.
Пусть
в точке О находится неподвижная
материальная точка, действующая на
частицу М с силой
;
—орт радиуса- вектора
,
-постоянная, равная -jm1m2
для
гравитационной и kq1q2
для кулоновской силы. Элементарная
работа этой силы на перемещении
:
;
Скалярное произведение—
приращение модуля вектора
;
Тогда
,
а работа на всем пути:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Движение центра масс системы
Допустим, что у нас есть некоторая система, состоящая из n -ного количества материальных точек. Возьмем одну из них и обозначим ее массу как m k . Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую F k e . Внутренние силы имеют равнодействующую F k l . Наша система находится в движении, следовательно, нужная точка будет иметь ускорение a k . Зная основной закон динамики, мы можем записать следующую формулу:
m k a k = F k e + F k l .
Ее можно применить к любой точке системы. Значит, для всей системы целиком можно сформулировать следующие уравнения:
m 1 a 1 = F 1 e + F 1 l , m 2 a 2 = F 2 e + F 2 l , ⋯ m n a n = F n e + F n l .
Данная формула состоит из дифференциальных уравнений, описывающих движение системы в векторной форме. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом.
Движение центра масс: основная теорема
Характер движения системы можно определить, зная закон, по которому движется ее центр масс.
Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором R , выражаемым через радиус-векторы r 1 , r 2 , . . . соответствующих материальных точек по формуле R = m 1 r 1 + m 2 r 2 + . . . + m n r n m .
Здесь сумма показателей в числителе m = m 1 + m 2 + . . . + m 3 выражает общую массу всей системы.
Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что:
∑ m k a k ¯ = ∑ F k ¯ e + ∑ F k ¯ l .
Взяв формулу радиус-вектора центра масс, получим следующее:
Теперь возьмем вторую производную по времени:
Здесь буквой a c ¯ обозначено ускорение, которое приобретает центр масс системы.
Свойство внутренних сил в системе гласит, что F k l равно нулю, значит, окончательное равенство будет выглядеть так:
M a c ¯ = ∑ F k ¯ e .
Это уравнение является записью закона движения центра масс. Запишем его:
Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы.
Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему.
Возьмем полученное выше уравнение и спроецируем его правую и левую части на соответствующие координатные оси. У нас получится:
M x c ¨ = ∑ F k x ¯ e , M y c ¨ = ∑ F k y ¯ e , M z c ¨ = ∑ F k z ¯ e .
Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат.
Практическое значение теоремы о движении центра масс
Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается.
- Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела.
- С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы.
Разберем пример применения теоремы для решения практической задачи.
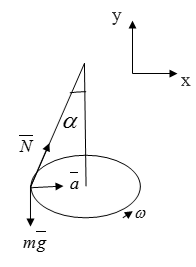
Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной ω . Вычислите, на каком расстоянии центр кольца находится от оси вращения.
Решение
Очевидно, что система находится под воздействием силы тяжести N N ¯ α α . Также необходимо учесть силу натяжения нити и центростремительное ускорение.
Второй закон Ньютона для системы будет выглядеть так:
Теперь создадим проекции обеих частей равенства на оси абсцисс и ординат и получим:
N sin α = m a ; N cos α = m g .
Мы можем разделить одно уравнение на другое:
Поскольку a = υ 2 R , υ = ω R , то нужное нам уравнение будет выглядеть так:
Определение центра масс
При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.
Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.
Радиус-вектор и координаты центра масс
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).
Из рис.1 видно, что:
Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:
Радиус -вектор $<overline>_C$, определенный выражением (2) — средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:
Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.
Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.
Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус — вектор, определяющий положение центра масс находим как:
Выражение (4) считают определением центра масс системы.
При этом абсцисса центра масс равна:
Ордината ($y_c$) центра масс и его аппликата ($z_c$):
Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.
Скорость центра масс
Выражение для скорости центра масс ($<overline>_c=frac>_c>
где $overline
$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.
Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.
Примеры задач на определение центра масс
Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?
Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:
Вычислим массу рассматриваемой системы точек:
Тогда абсцисса центра масс $x_ $равна:
Ответ. $x_c=0,5 b$; $y_с=0,3 b$
Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.
Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.
В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:
Физический факультатив. Тема: «Импульс, центр масс, движение центра масс»
В работе рассмотрены некоторые задачи на движение центра масс, рассматриваемые на школьном факультативе по физике в Лицее научно-инженерного профиля города Королева. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.
Импульс или количество движения материальной точки есть вектор, равный произведению массы этой точки m на вектор ее скорости v: 
Импульс силы – это вектор, равный произведению силы на время ее действия: 
Теорема об изменении импульса материальной точки. Пусть на материальную точку m действует постоянная сила F. Тогда


Импульс системы материальных точек равен по определению сумме импульсов всех N точек системы:
Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему.
Изолированная (замкнутая) система – это такая система материальных точек, на которую не действуют внешние силы или их равнодействующая равна нулю.
Закон сохранения импульса: импульс изолированной системы материальных точек сохраняется, каково бы ни было взаимодействие между ними:
Если внешние силы, действующие на систему не равны нулю, но существует такое неизменное направление (например, ось OX), что сумма проекций внешних сил на это направление равна нулю, то проекция импульса системы на это направление сохраняется.
Центр масс системы материальных точек. Центром масс N материальных точек m1, m2,…, mN, положения которых заданы радиус-векторами , называют воображаемую точку, радиус-вектор которой определяется формулой:
.
Тогда координаты центра масс равны:
,
,
.
Скоростью центра масс является вектор
,
где – скорость i-й точки.
Ускорением центра масс является вектор
где – ускорение i-й точки.
Теорема об ускорении центра масс системы материальных точек. Произведение суммы масс точек системы на ускорение центра масс равно сумме внешних сил, действующих на точки системы.
Если на систему материальных точек не действуют внешние силы, то скорость центра масс относительно любой инерциальной системы отсчета сохраняется, каково бы ни было взаимодействие внутри системы.
Если при этом скорость центра масс относительно некоторой инерциальной системы была равна нулю, то сохраняется и положение центра масс.
Два этих утверждения являются прямыми следствиями закона сохранения импульса.
Задача 1. Частица массы m движется со скоростью v, а частица массы 2m движется со скоростью 2v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2v направлении, обратном первоначальному. Определите скорость второй частицы. [1]
Изменение импульса частицы массой m вследствие действия импульса силы равно 3mv, следовательно вторая частица приобретает точно такой же импульс перпендикулярно направлению ее движения. Полный импульс второй частицы находится векторным сложением его составляющих по двум перпендикулярным направлениям и равен 5mv. Скорость второй частицы тогда равна 5v/2.
Задача 2. Ящик с песком массы М лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом ? к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, начав двигаться, остановится? При каком значении ? он вообще не сдвинется? [1]
Решение. Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему. По горизонтальной и вертикальной оси:
где u – скорость ящика сразу после того, как пуля в нем застрянет, N – реакция опоры, – время, за которое пуля застревает в песке. Из этих уравнений следует
Так как пуля застревает почти мгновенно последним членом в правой части можно пренебречь. После того, как пуля застрянет, ящик тормозит под действие силы трения с ускорением . Ящик останавливается за время . Ящик не сдвинется, если .
Задача 3. По наклонной плоскости, составляющей угол а с горизонтом, с постоянной скоростью v съезжает ящик с песком массой M. В него попадает летящая горизонтально пуля массой m, и ящик при этом останавливается. С какой скоростью u летела пуля?
Решение. Вдоль наклонной плоскости изменение импульса системы
Поперек наклонной плоскости
Тогда
и с учетом того, что (ящик съезжает с постоянной скоростью)
Задача 4. Обезьяна массы m уравновешена противовесом на блоке А. Блок А уравновешен грузом массы 2m на блоке В. Система неподвижна. Как будет двигаться груз, если обезьяна начнет равномерно выбирать веревку со скоростью u относительно себя? Массой блоков и трением пренебречь. [1]
Решение. Обезьяна получает импульс силы и начинает двигаться со скоростью v к потолку. Точно такой же импульс силы получает груз m и тоже движется со скоростью v к потолку. Груз массой 2m получает импульс силы и тоже движется со скоростью v к потолку. Блок А опускается вниз со скоростью v. груз m движется относительно блока А вверх со скоростью 2v. Веревка справа от блока А движется от потолка со скоростью 3v. относительно обезьяны веревка движется вниз со скоростью 4v. Отсюда .
Задача 5. Из однородной круглой пластины радиусом R вырезали круг вдвое меньшего радиуса, касающийся края пластины. Найти центр тяжести полученной пластины.
Решение. Пусть масса пластины до вырезания равна M. Тогда масса вырезанной части равна M/4. Предположим, что имеется в наличии вещество с отрицательной массой, Тогда вырез можно получить наложением на пластину пластинки с отрицательной массой —M/4. Тогда, поместив начало координат в центр круга и направив ось X направо, положение центра масс получаем из формулы для координаты центра масс:
.
Задача 6. На гладком полу стоит сосуд, заполненный водой плотности p0; объем воды V0. Оказавшийся на дне сосуда жук объема V и плотности p через некоторое время начинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным. [1]
Решение. Пусть скорость сосуда v, тогда скорость жука относительно пола u+v. Импульс системы по горизонтальной оси сохраняется и равен нулю. Удобно рассматривать жука как совокупность воды массой и сублимированного вещества жука массой , которое перемещается относительно всей воды. Тогда импульс системы
и
Задача 7. На дне маленькой запаянной пробирки, подвешенной над столом на нити, сидит муха, масса которой равна массе пробирки, а расстояние от поверхности стола равно длине пробирки l. Нить пережигают, и за время падения пробирки муха перелетает со дна в верхний конец пробирки. Определить время, за которое пробирка достигнет стола.
Решение. Ускорение центра масс системы определяется силами тяжести, действующими на пробирку и муху, и равно g. За время падения центр масс системы переместился на l/2. Отсюда время падения .
Задача 8. На нити, перекинутой через блок, подвешены два груза неравной массы (m2 > m1). Определить ускорение центра масс этой системы. Массой блока и нити пренебречь. [2]
Решение. Ускорение тяжелого груза направлено вниз и, как известно, равно . Ускорение легкого груза такое же по модулю, но направлено вверх. Ускорение центра масс находим по формуле из теоретического раздела
Задача 9. В сосуде, наполненном водой плотности p, с ускорением а всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m. [1]
Решение. Будем рассматривать системы как совокупность сосуда с водой массой и шарика с отрицательной массой , который поднимается вверх с ускорением a. Тогда ускорение центра масс системы
и направлено вниз. Из теоремы об ускорении центра масс
, и отсюда сила давления на опору, численно равная реакции опоры N,
Задачи для самостоятельного решения.
Задача 10. С горы с уклоном a () съезжают с постоянной скоростью сани с седоком общей массой M. Навстречу саням бежит и запрыгивает в них собака массой m, имеющая при прыжке в момент отрыва от поверхности горы скорость v, направленную под углом () к горизонту. В результате этого сани продолжают двигаться по горе вниз со скоростью u. Найти скорость саней до прыжка собаки. (Билет 3, 1991, МФТИ) [3]
Ответ:
Задача 11. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние S переместится лодка длиной L, если масса человека m, а масса лодки M? Сопротивлением воды пренебречь.
Ответ:
Задача 12. На поверхности воды находится в покое лодка. Человек, находящийся в ней, переходит с кормы на нос. Как будет двигаться лодка, если сила сопротивления движению пропорциональна скорости лодки?
Ответ: Лодка сместится, а затем вернется в исходное положение.
Задача 13. На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности p. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровней жидкости равна v. Полная масса всей системы m. [1]
Ответ:
Задача 14. На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности p. От сосуда параллельно полу отходит длинная и тонкая горизонтальная трубка, небольшой отрезок которой вблизи конца загнут по вертикали вниз. Расстояние от оси сосуда до отверстия трубки равно L. Уровень жидкости в сосуде опускается с ускорением а. Какой горизонтальной силой можно удержать тележку на месте? [1]
Ответ:
Литература.
1. Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. ? 2-е изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит. 1988. — 416 с.
2. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.
3. Методическое пособие для поступающих в вузы / Под. ред. Чешева Ю.В. М.: Физматкнига, 2006. – 288 с.
http://www.webmath.ru/poleznoe/fizika/fizika_114_opredelenie_centra_mass.php
http://urok.1sept.ru/articles/664163
Можаев В. Центр масс механической системы // Квант. — 2006. — №2. — С. 25-28.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Рассмотрим произвольную механическую систему твердых тел с заданным взаимным расположением в пространстве и с известными массами. Поступательное движение такой системы под действием внешних сил эквивалентно движению материальной точки, имеющей массу, равную массе системы, и находящейся под воздействием результирующей силы всех внешних сил.
Геометрическую точку, в которой располагается эта материальная точка, называют центром инерции или центром масс данной системы. Для произвольной неподвижной прямоугольной системы координат (ее называют также лабораторной системой) координаты центра масс определяются следующими формулами:
где mi, xi, yi, zi – массы и координаты центров масс тел, входящих в систему, а M – суммарная масса всех тел.
Если сумма внешних сил, действующих на систему, равна нулю, то центр масс остается неподвижным или движется прямолинейно с некоторой постоянной скоростью (в зависимости от предыстории). В этом случае удобно рассматривать движение тел под действием внутренних сил в инерциальной системе отсчета, связанной с центром масс. В такой системе отсчета импульс системы равен нулю и будет оставаться нулевым при любых взаимодействиях между телами системы.
Перейдем к разбору конкретных задач.
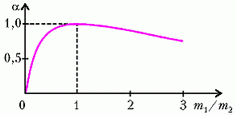
Задача 1. Определите, какую часть своей кинетической энергии теряет частица массой m1 при упругом лобовом столкновении с неподвижной частицей массой m2.
Пусть скорость налетающей частицы массой m1 равна υ1, тогда скорость движения центра масс системы будет равна
Перейдем в систему отсчета, связанную с центром масс нашей системы. В этой системе скорость частицы массой m1 равна
а скорость частицы массой m2 составляет
За положительное направление выбрано направление скорости первой частицы. Получается, чтов системе центра масс мы имеем уже другую ситуацию: обе частицы движутся навстречу друг другу с равными по величине импульсами
Когда частицы встретятся, возможны три варианта:
1) частицы не провзаимодействуют и пролетят, сохраняя свои скорости и импульсы;
2) произойдет нецентральный упругий удар, при котором частицы разлетятся, также сохраняя свои скорости и импульсы, но уже лежащие на прямой, проходящей по одному из диаметров сферы с центром в точке столкновения;
3) произойдет центральный упругий удар, при котором скорости и импульсы частиц также остаются неизменными по величине, но меняют свои направления на противоположные.
Найдем скорости наших частиц после центрального удара, но уже снова в неподвижной системе координат, где скорость частицы массой m1 до удара была υ1. После удара первая частица будет двигаться со скоростью
а вторая со скоростью
До удара кинетическая энергия налетающей частицы в неподвижной системе координат была
а после удара стала
Потеря кинетической энергии равна
что составляет от начальной энергии долю
Зависимость α от отношения m1/m2 изображена на рисунке 1. При m1 = m2 α = 1 т.е. происходит полная потеря энергии. При уменьшении отношения m1/m2 α уменьшается и при 
Рис. 1
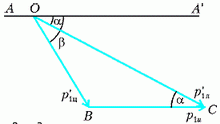
Задача 2. Две частицы, массы которых m1 и m2 (m1 > m2), движутся навстречу друг другу вдоль одной прямой с одинаковыми скоростями. После упругого столкновения тяжелая частица отклоняется от направления своего первоначального движения на угол α = 30° в лабораторной системе отсчета или на угол β = 60° в системе центра масс. Определите отношение m1/m2.
Обозначим начальные скорости частиц в лабораторной системе координат через υ0. Тогда скорость движения центра масс нашей системы частиц будет
– здесь за положительное направление выбрано направление скорости частицы массой m1.
Перейдем в систему координат, связанную с центром масс. В этой системе скорость частицы массой m1 до столкновения равна
Аналогичная скорость частицы массой m2 составляет
Импульсы частиц в этой системе координат равны по величине:
и направлены в противоположные стороны как до соударения, так и после него. Но после соударения импульсы частиц лежат на прямой, которая составляет угол β с направлением первоначального движения.
На рисунке 2 изображена векторная диаграмма импульсов для частицы массой m1.
Рис. 2
На этой диаграмме прямая АА´ соответствует направлению первоначального движения частиц. Отрезок ОВ равен импульсу частицы массой m1 в системе центра масс после столкновения, отрезок ОС равен импульсу этой же частицы после соударения, но уже в лабораторной системе отсчета. А вот отрезок ВС – это импульс, который добавляется при переходе из системы центра масс в лабораторную систему, величина этого импульса равна
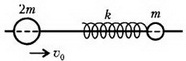
При заданных значениях углов α и β треугольник ОВС оказывается равнобедренным, поскольку угол BOC = β – α = 30º, a угол BCO = α = 30º (BC || AA´). Из этого следует, что ОВ = ВС, или
откуда получаем
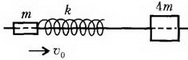
Задача 3. На прямолинейную горизонтальную спицу насажены два шарика, которые могут скользить по ней без трения (рис. 3). К шарику массой m прикреплена легкая пружина жесткостью k. Эта система неподвижна, а шарик массой 2m движется со скоростью υ0. Определите скорость шарика массой 2m после отрыва от пружины и время контакта этого шарика с пружиной. Радиусы шаров много меньше длины пружины.
Рис. 3
Скорость центра масс в лабораторной системе координат составляет
Перейдем в систему отсчета, связанную с центром масс. Скорость шарика массой 2m до взаимодействия с пружиной в этой системе равна
а скорость шарика массой m направлена в противоположную сторону и равна по величине
Как только шарик массой 2m достигнет пружины, скорости шариков начнут уменьшаться, а пружина будет сжиматься. В некоторый момент, когда вся кинетическая энергия шариков перейдет в потенциальную энергию упругой деформации пружины, шарики остановятся, а затем начнут ускоряться в противоположных направлениях. Когда пружина примет свою первоначальную длину, шарик массой 2m оторвется от пружины и будет иметь скорость, равную υ1ц и направленную в другую сторону по отношению к первоначальной. Но это – скорость в системе центра масс, а нам нужно найти скорость этого шарика в лабораторной системе отсчета.
Для этого перейдем обратно в лабораторную систему отсчета. В этой системе скорость шарика массой 2m, очевидно, будет равна
Относительная потеря кинетической энергии шарика составит
Для проверки воспользуемся результатом, полученным в задаче 1:
Это совпадение закономерно, поскольку данная задача является частным случаем задачи 1 при m1/m2 = 2.
Для ответа на второй вопрос заметим, что когда шарик массой 2m находится в контакте с пружиной, эта ситуация эквивалентна колебаниям шарика на горизонтально расположенной пружине, один конец которой закреплен. Закрепленным концом является центр масс, который остается неподвижным в системе отсчета, связанной с центром масс. Если длина нашей пружины l, то длина эквивалентной пружины составляет
Теперь нужно сообразить, чему будет равна жесткость пружины длиной lэкв, если жесткость исходной пружины k. Это право мы предоставляем читателю, а сами напишем готовый результат:
Очевидно, что время контакта шарика массой 2m с пружиной равно половине периода гармонических колебаний шарика на эквивалентной пружине:
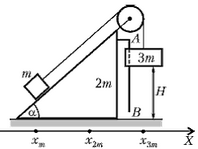
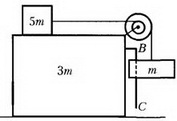
Задача 4. Клин массой 2m с углом наклона к горизонту α (cos α = 2/3) находится на гладкой горизонтальной поверхности стола (рис. 4). Через блок, укрепленный на вершине клина, перекинута легкая нить, связывающая грузы массами m и 3m. Груз массой 3m может скользить вдоль вертикальной направляющей AB, закрепленной на клине. Этот груз вначале удерживают неподвижно на расстоянии Н = 27 см от стола, а затем отпускают. На какое расстояние сместится клин к моменту касания груза массой 3m стола? Массами блока и направляющей AB пренебречь.
Рис. 4
После того как отпустили груз массой 3m, на нашу систему тел в горизонтальном направлении (ось X) никакие внешние силы не действуют, поэтому горизонтальная координата центра масс системы будет оставаться неизменной. Пусть в произвольный момент времени (после освобождения груза массой 3m) горизонтальные координаты центров масс трех тел будут такими: xm – координата груза массой m, х2m – координата клина, x3m – координата груза массой 3m (начало отсчета – произвольное). Тогда горизонтальная координата центра масс системы будет равна
Поскольку величина xц остается постоянной, можно записать
xm + 2x2m + 3x3m = const.
За время падения груза массой 3m происходит изменение всех трех координат, причем эти изменения будут связаны между собой соотношением
Δxm + 2Δx2m + 3Δx3m = 0,
или, так как Δx2m = Δx3m,
Δxm + 5Δx2m = 0.
Опускание груза массой 3m на величину H приводит к перемещению груза массой m вдоль наклонной плоскости также на H, а вдоль оси X – на H·cos α. Но это – перемещение относительно клина, а полное горизонтальное перемещение груза массой m будет равно
Δxm = H·cos α + Δx2m.
Тогда, с учетом соотношения между Δxm и Δx2m, для перемещения клина получим
Знак «минус» означает, что клин сместится влево.
Задача 5. Определите минимальное значение кинетической энергии α-частицы, необходимое для осуществления реакции 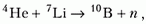
До реакции мы имеем α-частицу, или ядро атома гелия, и ядро лития, а после реакции образуются ядро бора и нейтрон. Если мы подсчитаем суммарные энергии покоя частиц до реакции и после реакции, то увидим, что энергия покоя ядра бора и нейтрона больше, чем энергия покоя α-частицы и ядра лития. Эта разность как раз и равна поглощаемой энергии Q при данной реакции. Такие ядерные реакции, проходящие с поглощением энергии, называют эндотермическими реакциями. Реакции, идущие, наоборот, с выделением энергии, называют экзотермическими. Отсюда понятно, что если исходные частицы неподвижны, то эндотермическая реакция не пойдет. Значит, налетающая на мишень частица должна обладать некоторой минимальной энергией, при которой начнется реакция. Величину этой энергии называют пороговой.
Наиболее удобно рассмотреть процесс неупругого взаимодействия частиц в системе отсчета, связанной с центром масс системы. Обозначим скорость α-частицы в лабораторной системе отсчета через υα. Тогда скорость движения центра масс равна
где mα и mLi – массы α-частицы и ядра лития. Скорость α-частицы в системе центра масс составляет здесь за положительное направление выбрано направление скорости α-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна
– здесь за положительное направление выбрано направление скорости α-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна
В этой системе отсчета при пороговой скорости α-частицы образовавшееся ядро бора и нейтрон должны покоиться. Запишем закон сохранения полной энергии до реакции и после реакции:
– энергии частиц здесь записаны для нерелятивистского случая. Подставляя в это уравнение выражения для υαц и учитывая, что
получим
Отсюда находим минимальную кинетическую энергию α-частицы в лабораторной системе отсчета:
Упражнения
1. Вдоль прямолинейной горизонтальной спицы могут скользить без трения две муфты. Муфта массой m с прикрепленной к ней легкой пружиной жесткостью k движется со скоростью υ0, а муфта массой 4m покоится (рис. 5). Определите скорость муфты массой 4m после ее отрыва от пружины и время контакта этой муфты с пружиной. Размеры муфт много меньше длины пружины.
Рис. 5
2. На гладкой горизонтальной поверхности стола находится брусок в форме прямоугольного параллелепипеда, на котором укреплены ступенчатый блок с радиусами шкивов r и R (R = 4r) и вертикальная штанга ВС (рис. 6). На шкивы намотаны легкие нити, прикрепленные к грузам массами m и 5m. Груз массой m может скользить вдоль штанги ВС. Вначале груз массой 5m удерживают в покое, а затем отпускают. К моменту удара груза массой m о стол другой груз не достигает блока, а брусок за это время смещается на расстояние s = 2,5 см. На каком расстоянии от стола находился груз массой m вначале? Массами блока и штанги пренебречь.
Рис. 6
3. Движущаяся частица претерпевает упругое столкновение с покоящейся частицей такой же массы. Докажите, что после столкновения, если оно не было лобовым, частицы разлетятся под прямым углом друг к другу.
4. Какова кинетическая энергия α-частицы, если при попадании в ядро азота 14N происходит реакция 
Ответы
1.
2.
4. Ek = 1,3 МэВ.