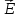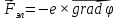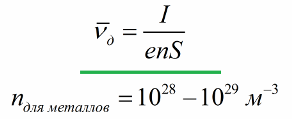Как найти скорость электронов от напряжения

4

Электронная
микроскопия

Лекция
№7

Из уравнения (8)
следует, что скорость электрона выражается
через ускоряющее напряжение как

(9)

Известно, что длина
волны частицы
связана с его массой
и скоростью
уравнением Де-Бройля. (Де Бройль перенес
корпускулярно-волновой дуализм в
отношении излучения
на частицы, обладающие массой покоя,
каковыми и являются электроны)

(10)

Если в это уравнение
подставить найденное нами выражение
скорости электрона, находящегося в поле
ускоряющего напряжения U,
то получим

(11)

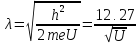
где λ
получится в ангстремах, если напряжение
подставить в вольтах. Длина волны,
вычисленная таким образом называется
дебройлевской.

Если ускоряющее
напряжение более 50 кВ, то нужно учитывать
релятивистскую поправку, и вместо U
использовать выражение для U^*

(12)

Как электрон
движется в электростатическом поле

Электростатическое
поле характеризуется двумя величинами:

• скалярным
  потенциалом φ
  и

• вектором
  напряженности
  .

Потенциал
поля в некоторой точке определяется
работой,
которую необходимо затратить на
перемещение единичного положительного
заряда из бесконечности (или другой
точки пространства с
условно
принятым нулевым потенциалом) в данную
точку.

Разность
потенциалов
между двумя точками, или приложенное к
этим точкам напряжение, очевидно, равна
работе,
затрачиваемой на перемещение заряда
из одной точки в другую.

Напряженность
поля Ε
равна
силе,
с которой поле действует на единичный
положительный заряд.

Для электрона,
имеющего отрицательный заряд —е,
эта сила

(13)

Для определения
направления вектора напряженности
удобно электростатическое поле
представить с помощью эквипотенциальных
поверхностей,
т.е. геометрических
мест точек с одинаковым потенциалом: φ
= const.

Тогда вектор
напряженности

• будет направлен
  перпендикулярно
  к поверхности равного потенциала

• в сторону уменьшения
  потенциалов.

Очевидно, что чем
гуще будут расположены эквипотенциальные
поверхности, тем большую энергию
приобретает электрон за единицу длины
своего пути.

Напряженность
поля и
характеризует эту «густоту»
эквипотенциальных поверхностей, или
скорость
изменения потенциала,
выражаемую так называемым градиентом
потенциала. Таким образом,

(14)

и уравнение (4)
приобретает вид

(15)

Следовательно, в
электростатическом поле электрон будет
двигаться вдоль градиента потенциала
в сторону увеличения последнего.

Точное совпадение
траектории движения электрона с силовой
линией (т. е. линией, перпендикулярной
к эквипотенциальным поверхностям) может
и не иметь места, так как при переходе
из одной области поля в другую электрон,
изменяя свою скорость, будет частично
сохранять направление движения, которое
он имел ранее. Тем не менее, при переходе
через эквипотенциальные поверхности
траектория электрона будет изменяться,
т. е. электрон будет испытывать преломление.

Преломление
электронов в электрическом поле.

Физической основой
формирования светооптического изображения
является преломление светового луча
на границе раздела двух сред (например,
воздуха и стекла линзы).

Учитывая, что и
траектория электрона испытывает
преломление при переходе через области
с разными потенциалами, рассмотрим по
аналогии со световой оптикой закон
преломления электронов в электрическом
поле.

Рассмотрим
пространство, разделенное двумя
близлежащими металлическими сетками
с потенциалами φ_χ
и φ₂

Рис. Преломление
траектории электрона при скачкообразном
изменении потенциала

Приближенно можно
считать, что потенциал в каждой области
постоянен и равен соответственно φ₁
и φ₂.

Пусть υ₁
—
скорость, с которой электрон из области
I подходит к двойному разделяющему
слою—преломляющей границе, а υ₂
—скорость,
с которой он выходит из этого слоя в
область II.

Углы α₁
и α₂
назовем углами падения и преломления.
Разложим вектор скорости на две
составляющие: υ’
и υ».

Из определения
напряженности электрического поля
очевидно, что на электрон, пересекающий
двойной слой, будет действовать сила,
перпендикулярная
поверхности сетки — поверхности равного
потенциала.

Отсюда следует,
что составляющая скорости электрона,
направленная параллельно слою, останется
неизменной, т. е.

υ’₁
= υ’₂

или

υ₁sin
α₁
= υ₂sin
α₂

Но как следует из
формулы (16)

(16)

(17)

что после подстановки
в выражение (22) дает

(18)

Сравнивая это
выражение с законом преломления в
световой оптике, мы видим, что получается
полная аналогия, если для электроннооптического
показателя преломления принять (с
точностью до постоянного множителя)
величину n

.
(19)

Модель такого
двойного электрического слоя может
быть осуществлена при помощи двух
параллельных сеток.

Если электрон
ускоряется, то, пройдя двойной слой, он
приближается в большей или меньшей
степени к нормали. Если электрон
тормозится, то его траектория отходит
от нормали.

Двойной слой
действует как отражающий, если внутри
его начальная нормальная компонента
v_xcos
обращается
в нуль.

Полученный закон
преломления остается справедливым и в
том случае, если двойной преломляющий
слой образован не плоскими, а криволинейными
поверхностями и если изменение потенциала
в переходной области сколь угодно мало.

Поэтому
эквипотенциальные
поверхности электростатического поля
также можно рассматривать как поверхности
изменения потенциала, на которых электрон
претерпевает преломление.

Таким образом, на
основании аналогии между законами
преломления световых и электронных
лучей, лежащей в основе всей электронной
геометрической оптики, можно утверждать,
что эквипотенциальные поверхности
электрического поля являются аналогами
преломляющих поверхностей линз в
световой оптике.

Следовательно,
создавая с помощью заряженных электродов
определенной конфигурации требуемую
форму эквипотенциальных поверхностей,
можно получить электрическое поле,
обладающее необходимыми оптическими
свойствами для получения электроннооптических
изображений.

Наряду с указанной
аналогией между световой и электронной
оптикой имеется и существенное различие.

• В световой оптике
  для получения изображений используются
  однородные
  среды
  (воздух, стекло, иммерсионные жидкости),
  где показатель преломления изменяется
  дискретно, скачкообразно переходя на
  границе раздела от одного значения к
  другому.

• В электростатическом
  поле показатель
  преломления меняется непрерывно
  и является функцией координат
  рассматриваемой точки пространства.
  Следовательно, электрическое поле
  действует как оптически неоднородная
  среда.

/var/www/studfiles2/data/www/download/2706/299/26VLaKENRD.mZO5

Соседние файлы в папке Новая папка

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Скорость электрического тока

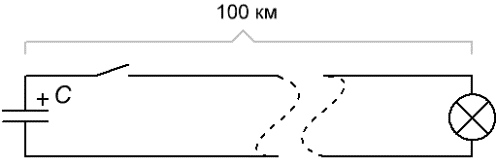
Давайте проведем такой мысленный эксперимент. Представьте, что на расстоянии в 100 километров от города находится некая деревня, и что из города в эту деревню проложена проводная сигнальная линия длиной примерно в 100 километров с лампочкой на конце. Линия экранированная двухпроводная, она проложена на опорах вдоль автомобильной дороги. И если теперь послать сигнал по этой линии из города в деревню, то через какое время он сможет быть там принят?

Расчеты и опыт говорят нам, что сигнал в виде засветившейся лампочки появится на другом конце минимум через 100/300000 секунд, то есть минимум через 333,3 мкс (без учета индуктивности провода) в деревне загорится лампочка, значит в проводнике установится ток (допустим, мы используем постоянный ток от заряженного конденсатора).

100 — это длина каждой из жил нашего провода в километрах, а 300000 километров в секунду — скорость света — скорость распространения электромагнитной волны в вакууме. Да, «движение электронов» распространится по проводнику со скоростью света.

Но тот факт, что электроны начинают приходить в движение друг за другом со скоростью света вовсе не означает, что сами электроны движутся в проводнике со столь огромной скоростью. Электроны или ионы, в металлическом проводнике, в электролите или в другой проводящей среде, не могут двигаться так быстро, то есть носители заряда не движутся друг относительно друга со скоростью света.

Скорость света в данном случае — это та скорость, с которой носители заряда в проводнике начинают друг за другом приходить в движение, то есть это скорость распространения поступательного движения носителей заряда. Сами же носители заряда имеют «дрейфовую скорость» при установившемся токе, скажем в медном проводнике, всего несколько миллиметров в секунду!

Поясним этот момент. Допустим, у нас есть заряженный конденсатор, и мы присоединяем к нему длинные провода от нашей лампочки, установленной в деревне на расстоянии в 100 километров от конденсатора. Присоединение проводов, то есть замыкание цепи осуществляем выключателем вручную.

Что произойдет? При замыкании выключателя начинается движение заряженных частиц в тех частях проводов, которые присоединены к конденсатору. Электроны покидают минусовую обкладку конденсатора, электрическое поле в диэлектрике конденсатора уменьшается, положительный заряд противоположной (плюсовой) обкладки уменьшается — на нее забегают электроны из присоединенного провода.

Так разность потенциалов между обкладками уменьшается. А так как электроны в прилегающих к конденсатору проводах начали двигаться, то на их места приходят другие электроны из отдаленных мест провода, иначе говоря начинается процесс перераспределения электронов в проводе из-за действия электрического поля в замкнутой цепи. Этот процесс распространяется все дальше и дальше по проводу и наконец достигает нити накаливания сигнальной лампы.

Итак, изменение электрического поля распространяется по проводнику со скоростью света, активируя электроны в цепи. Но сами электроны движутся гораздо медленнее.

Прежде чем пойти дальше, рассмотрим гидравлическую аналогию. Пусть из деревни в город по трубе подается минеральная вода. Утром в деревне запустили насос, и он стал повышать давление воды в трубе, чтобы заставить воду из деревенского источника двигаться в город. Изменение давления распространяется по трубопроводу очень быстро, примерно со скоростью 1400 км/с (зависит от плотности воды, от ее температуры, от величины давления).

Спустя долю секунды после пуска насоса в деревне, вода начала двигаться уже в городе. Но та же ли это вода, что движется в данный момент в деревне? Нет! Молекулы воды в нашем примере толкают друг друга, а сами движутся значительно медленнее, поскольку скорость их дрейфа зависит от величины напора. Толкотня молекул между собой распространяется на много порядков быстрее чем движение молекул вдоль трубы.

Так и с электрическим током: скорость распространения электрического поля аналогична распространению давления, а скорость движения электронов, образующих ток, аналогична движению непосредственно молекул воды.

Теперь вернемся непосредственно к электронам. Скорость упорядоченного движения электронов (или других носителей заряда) называют дрейфовой скоростью. Ее электроны приобретают благодаря действию внешнего электрического поля.

Если внешнего электрического поля нет, то электроны движутся хаотично внутри проводника лишь в тепловом движении, но направленного тока нет, и следовательно дрейфовая скорость в среднем оказывается равной нулю.

Если внешнее электрическое поле приложено к проводнику, то в зависимости от материала проводника, от массы и заряда носителей заряда, от температуры, от разности потенциалов, — носители заряда придут в движение, но скорость этого движения будет существенно меньше скорости света, порядка 0,5 мм в секунду (для медного проводника сечением 1 мм2, по которому течет ток 10 А, средняя скорость дрейфа электронов составит 0,6–6 мм/c).

Эта скорость зависит от концентрации свободных носителей заряда в проводнике n, от площади сечения проводника S, от заряда частицы e, от величины тока I. Как видите, несмотря на то, что электрический ток (фронт электромагнитной волны) распространяется по проводнику со скоростью света, сами электроны движутся куда медленнее. Получается, что скорость тока — это очень малая скорость.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Скорость движения электронов

Уже упоминалось, что электроны движутся в направлении анода ускоренно, и это без всяких преувеличений соответствует действительности. В тот момент, когда электрон покидает область катода, его скорость теоретически принимается равной нулю, однако, он, находясь в постоянном электрическом поле анода, начинает дви­гаться ускоренно, и приобретает энергию, пропорциональную ускоряющему напря­жению:

е — заряд электрона, принимается равным ≈ 1,602 х 10 -19 Кл;

т_е — масса электрона, принимается равной ≈ 9,11 х 10 -31 кг;

Решая это уравнение относительно скорости электрона υ, получим следующее выражение:

В науке часто используется отношение заряда электрона к его массе, е/т_е, кото­рое имеет приближенное значение 1,7588 х 10 11 Кл/кг. При приложении к аноду относительно катода напряжения 100 В электрон достигнет поверхности анода, имея скорость порядка 6 х 10 б м/с.

Если использовать предыдущее выражение и подставить в него ускоряющее на­пряжение 512 кВ, (величина, соответствующая, например, напряжению в дальних линиях электропередач), то получится, что скорость электрона может превысить ско­рость света, что, естественно, является невозможным. Причина заключается в том, что приведенное упрощенное выражение справедливо только для массы покоя элект­рона, однако, при движении с околосветовыми скоростями масса электрона возрас­тает, требуя бесконечно большого значения напряжения для ускорения электрона до околосветовых скоростей. С учетом этих условий необходимо использовать более сложное уравнение, предложенное Элли (Alley) и Этвудом (Atwood):

в котором с — скорость света в вакууме, примерно равна 2,998 х 10 8 м/с.

В качестве домашнего примера действие принципа относительности можно про­демонстрировать на цветном телевизоре. Для исправного цветного кинескопа напря­жение на втором аноде составляет порядка 25 кВ, поэтому скорость электрона в мо­мент удара о поверхность кинескопа составляет более 300 млн км/час, однако более простое уравнение предсказывает скорость, на 3,5% более высокую.

В рентгеновских медицинских установках мишень бомбардируется электронами, имеющими очень высокую скорость, так как для возникновения рентгеновского излу­чения скорость электрона при соударении должна значительно превышать 300 млн км в час. Поэтому в кинескопах домашних телевизоров и мониторов (для снижения интенсивности рентгеновского излучения) не используется ускоряющее напряжение, превышающее 25 кВ, хотя при этом можно было бы обеспечить более высокую чет­кость и фокусировку изображения.

Необходимо учесть, что расстояние между анодом и катодом не входит в каждое из уравнений, хотя теоретически бесконечное расстояние позволило бы бесконечно возрасти времени, во время которого происходит ускорение движения, и даже при сравнительно небольших ускорениях скорость при ударе могла бы оказаться значи­тельной.

Очень многие явления, происходящие внутри электронных ламп, могут быть по­няты при понимании процессов, происходящих при ускоренном движении электрона в электрическом поле анода, приобретении им кинетической энергии и процессах пе­редачи энергии электрона при ударе, когда он достигает анода.

Все сказанное выше вполне справедливо для обсуждения скоро­сти движения ускоренных положительным полем электронов, подлетающих к аноду. Однако в области катода картина совсем иная. Дело в том, что кинетическая энергия электронов, преодолевших работу выхода из металла и покинувших катод, оказыва­ется различной. Таким образом, отрываясь от катода, электроны начинают движение к аноду с различными начальными скоростями. Они невелики, но при детальном рас­смотрении их нельзя считать одинаковыми, как это предполагалось выше, когда рас­сматривался ускоренный поток электронов, подлетающих к аноду. Как будет показа­но ниже, управление электронным потоком в триодах и более сложных электронных лампах осуществляется как раз вблизи катода. Из физической статистики известно, что из-за различных кинетических энергий, скорости электронов, вылетающих из ка­тода распределены по так называемому закону распределения Максвелла. Однако, для дальнейших рассуждений наиболее важным фактом является тот факт, что элек­троны, вылетающие из катода, обладают различными кинетическими энергиями.

Источник

С какой скоростью перемещается электрический ток по проводам

Вы, наверное, сразу же скажете, что скорость электрического тока равна скорости света и будете неправы. В этом материале я на простом примере объясню, каким образом и с какой скоростью перемещается электрический ток по проводам.

Давайте для примера смоделируем следующую ситуацию:

Пусть у нас будет лампочка соединенная с постоянным источником питания двужильным экранированным кабелем, причем длина этого кабеля будет 10 километров.

Теперь если мы включим выключатель в этой цепи, то лампочка загорится через 10 км/300 000 км/с, где 10 км — это длина нашего проводника, а 300 000 км/с — это скорость распространения электромагнитной волны (света) в вакууме.

То есть, произведя расчет, получается, лампочка загорится через 0,00003333 сек или 33,333 мксек (в расчет не принята емкость проводника). Из этого следует вывод, что «движение электронов» распространится по проводнику со скоростью света.

Но то обстоятельство, что электроны начинают перемещаться друг за другом со скоростью света совсем не говорит о том, что они перемещаются в проводнике с этой же скоростью.

Здесь скорость света эта та скорость, с которой заряженные частицы начинают двигаться друг за другом, а перемещаться по проводнику они могут со скоростью всего лишь несколько миллиметров в единицу времени.

Непонятно? Сейчас объясню почему так.

Итак, мы замкнули цепь, нажав выключатель. В этот момент электроны начинают покидать минусовую клемму нашего с вами конденсатора, при этом происходит уменьшение электрического поля в диэлектрике конденсатора и электроны (с подключенного проводника) начинают заходить на плюсовую клемму конденсатора.

Таким образом, разность потенциалов между обкладками конденсатора уменьшается. А по причине того, что электроны в присоединённом участке проводника пришли в движение, то их пустующее место занимают электроны из соседнего участка провода (под действием электромагнитного поля замкнутой цепи).

Этот процесс перемещения распространяется все дальше по проводнику и по истечению определенного времени достигает нашей с вами лампочки и протекающий ток заставляет ее светиться.

Получается, что изменение электрического поля по проводнику распространяется мгновенно, а вот сами заряженные частицы имеют гораздо более низкую скорость.

Аналогия с водопроводом

Давайте для простоты понимания проведем аналогию с водопроводом.

Представьте такую картину: вы запустили водяной насос, также находящийся далеко за городом и буквально через доли секунды (изменение давления распространяется со средней скоростью 1400 км/с) у вас из трубы начала поступать вода. Но эта не та же самая вода, которая только что прошла через насос, «толкотня» молекул воды распространилась с огромной скоростью, а сами молекулы движутся с гораздо меньшей скоростью.

Так и с движением электрического тока.

А как у переменного тока

Ну вроде бы с постоянным током все более-менее стало ясно и может так же возникнуть второй логичный вопрос: А как дела обстоят с переменным током?

На самом деле разница здесь заключена лишь в том, что переменный ток меняет направление своего движения с частотой 50 Герц в единицу времени. Но при этом его скорость зависит все от тех же факторов, что и в случае с постоянным током.

Заключение и выводы

Так, давайте вновь вернемся к току. Получается, если на проводник не воздействует электромагнитное поле, то движение электронов внутри провода происходит абсолютно в хаотичном порядке.

Как только к проводнику оказывается воздействие электрического поля, то в зависимости от таких факторов как температура проводника, материала, разности потенциалов, скорость электрического тока может варьироваться от 0,6 до 6 миллиметров в одну единицу времени. Как видите, эта величина очень далека от скорости света. И вычисляется она по следующей формуле:

Где n – концентрация свободных носителей, S – площадь сечения проводника, e – заряд частицы, I – сила тока.

Это все, что я хотел вам рассказать о скорости перемещения электрического тока по проводам. Если статья оказалась вам полезна, то оцените ее лайком. Спасибо за ваше внимание!

Источник

Зависимость скорости электрона от напряженности электрического поля. Понятия эффективной массы и подвижности.

электрический ток в образце зависит не только от концентрации носителей заряда, но и от скорости с которой они переносятся под действием электрического поля. После того как мы научились рассчитывать концентрацию свободных носителей в твердом теле рассмотрим как ведут себя носители заряда в кристалле при наложении на него электрического поля.

Рассмотрение начнем с поведения единичного свободного заряда в нейтральной не взаимодействующей с зарядом среде (допустим в вакууме) при наличии электрического поля E, которое накладывается на среду в момент t=0. Электрическое поле приводит к возникновению силы электростатического взаимодействия F, под действием которой электрон начнет ускоряться.

, (1.25)

где q, m – заряд и масса электрона, v и a его скорость и ускорение. Таким образом в электрическом поле заряженная частица разгоняется с постоянным ускорением пропорциональным напряженности электрического поля и обратно пропорциональным ее массе. При этом энергия частицы будет изменяться со временем по квадратичному закону относительно импульса частиц или ее волнового вектора k (p= ћ k, где ћ = h/(2π), h – постоянная Планка).

(1.26)

Поскольку приобретаемая заряженной частицей энергия не зависит от направления электрического поля зависимость (1.5) симметрична относительно импульса и волнового вектора (это параболоид выпуклость которого определяется массой частицы).

Измерив зависимость энергии частицы от импульса (или волнового числа мы можем ) используя (1.5) определить эффективную массу. Действительно дважды продифференцировав (1.5) получим.

(1.27)

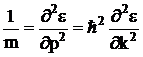
Предположим, что на частицу действует некоторая тормозящая сила F* о существовании которой мы не знаем. Тогда уравнение (1.4) можно переписать в следующем виде:

(1.28)

Соответственно, если для определения массы электрона (или любой другой заряженной частицы) в некоторой взаимодействующей с частицей среде воспользуемся формулой (1.6), то вместо массы электрона будет рассчитана некоторая другая величина, которую будем назвать эффективной массой электрона в данной среде.

(1.29)

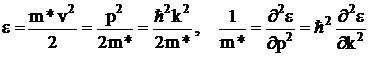
Поскольку при движении электронов (или других заряженных частиц) в твердом теле внутренние поля неизвестны, то их характеристики используют понятие эффективной массы.

Рис. 1.18. Изменение скорости заряженной частицы в электрическом поле, при отсутствии взаимодействия со средой(1) и при торможении частицы средой.

На рис. 1.5 показано как будет со временем изменяться скорость свободной частицы в электрическом поле, в соответствии с (1.4) и (1.7 ). Эти формулы справедливы для случая, когда заряженная частица не испытывает столкновений и в соответствии с ними частицу можно разогнать электрическим полем до бесконечной энергии. Именно этот принцип был использован в первых линейных ускорителях элементарных частиц.

По мере разгона частицы возрастает ее импульс и соответствующее ему волновое число (величина, характеризующая величину волнового вектора). На рис. 1.6. показаны соответствующие зависимости изменения энергии частицы от величины волнового числа (импульса).

Рис. 1.19. Зависимости энергии свободных зарядов от величины их волнового числа (импульса).

Как видно из рис. 1.18. и рис. 1.19 набираемая в электрическом поле энергия частицы зависит от скорости частицы (волнового числа) и массы. Поскольку выпуклость кривой характеризуется ее второй производной можно сделать вывод, что чем меньше эффективная масса частицы, тем больше выпуклость, см. (1.27) и (1.29).

В кристалле энергия электрона (дырки) в разрешенной зоне не может превысить значение потолка разрешенной зоны, следовательно импульс и волновой вектор так же имеют ограничения, причем максимальное значение волнового числа должно быть кратно постоянной решетки. На рис. 1.20 показана рассчитанное изменение энергии электрона от величины волнового числа (значения) импульса для кубического кристалла.

Рис. 1.20. Зависимость энергии от волнового числа (импульса) в кристалле (a – постоянная решетки вдоль заданного направления)

Из рисунка видно, что в электронном представлении у потолка валентной зоны знак эффективной массы изменяется (должно происходить отражение частицы). Следует отметить, что у дна зоны проводимости энергия имеет параболическую зависимость от импульса (волнового числа):

(1.31)

Если вести отсчет от дна зоны проводимости E_c = 0, то зависимость энергии электрона от импульса (волнового вектора) будет такая же как для свободного электрона см. (1.26). Это дает нам основание рассматривать электроны в зоне проводимости, находящиеся вблизи дна зоны проводимости как свободные частицы (иногда говорят квазисвободные или квазичастицы), считая что они подчиняются тем же закономерностям, что и свободные частицы, но отличаются от них величиной эффективной массы, которую вблизи дна зоны можно считать постоянной (пока выполняется параболическое приближение).

Аналогичный подход справедлив и для дырки. Вводя дырку мы переходим от электронного представления к дырочному, т.е. мы принимаем, то масса дырки положительная, а заряд отрицательный и энергия ее отсчитывается от потолка валентной зоны к ее дну, тогда дырка будет вести себя так же как электрон у потолка валентной зоны. При этом энергия дырки у потолка валентной зоны так же изменяется по параболическому закону как и для электрона:

(1.32)

Таким образом дырку, находящуюся потолка валентной зоны так же можно рассматривать как свободную частицу.

В реальной жизни электрон в электрическом поле не может набирать энергию до бесконечности, рано или поздно он столкнется с другой частицей и отдаст ей накопленную энергию. Вероятность столкновений частиц в газах и твердых телах характеризуется временем или длиной их свободного пробега. Эти же величины характеризуют движение носителей заряда в твердом теле.

Схема, приведенная на рис. 1.21 показывает изменение скорости электрона в образце, к которому приложено напряжение и поясняет физический смысл подвижности. Электрон участвует в хаотическом тепловом движении, причем в различные моменты времени его скорость имеет случайное направление так что смещение его в любом направлении равновероятно. В электрическом поле электрон приобретает дополнительную скорость под действием поля, так что продолжая участвовать в тепловом движении он постепенно смещается под действием поля. Средняя скорость тем выше, чем больше длина свободного пробега и чем меньше эффективная масса частицы.

Рис. 1. 21. Диаграмма, поясняющая движение электрона в твердом теле

Поскольку электрон набирает энергию в поле за время свободного пробега и отдает ее при столкновении с решеткой или другими носителями заряда, то средняя скорость, которую приобретают носители в направлении поля, будем называть ее скоростью дрейфа зарядов v_др должна зависеть от средней длины свободного пробега τ.

(1.36)

Коэффициент пропорциональности между дрейфовой скоростью и напряженностью электрического поля обычно называют подвижностью носителей заряда и обозначают μ:

Как видно из (1.36) и (1.37) подвижность имеет размерность в системе СИ м 2 /(Вс) , широко так же используются значения подвижности с размерностью см 2 /(Вс).

Предположим, что ток через ток образце создается электронами концентрация которых n см -3 и средняя дрейфовая скорость v_др. Поскольку величина тока равна заряду, проходящему через сечение образца в единицу времени можем записать:

Для единичной площади из (1.35) получится уравнение для плотности тока:

Поскольку в дифференциальной форме закон Ома имеет вид:

где σ – электропроводность образца (Ом . м или Ом . см )

Сравнив (1.39) и (1.40) получим формулу для электропроводности:

Если электрический ток создается различными носителями (всего N типов) с концентрацией каждого типа n_i , то:

(1.42)

таким борзом мы видим, что проводимость материала определяется двумя основными параметрами: подвижностью носителей заряда и их концентрацией.

Величина подвижности пропорциональна длине свободного пробега, которая зависит от частоты столкновений носителей заряда с решеткой или атомами примеси. Поскольку при столкновениях носители отдают энергию, а затем вновь набирают, т.е. энергия носителя релаксирует, то принято говорить о механизмах ее релаксации. За время релаксации принимают среднее время в течение которого электрон полностью отдает свою энергию.

Существует множество механизмов рассеяния (релаксации ) энергии свободных носителей заряда. Однако, для полупроводников, наиболее существенные два: рассеяние на решетки и рассеяние на ионизованной примеси.

Для рассеяния на решетке справедливо :

T -3/2 и с ростом температуры подвижность носителей падает. Действительно длина свободного пробега носителей заряда тем меньше, чем сильнее колеблется решетка l

1/T , для скорости носителей справедливо v

1/T 3/2 . Таким образом рост, в случае если доминирует рассеяние на решетке (примесей мало), то с ростом температуры подвижность падает и следовательно падает проводимость ( как это имеет место в металлах).

При рассеянии на заряженной примеси μ_i

Таким образом, если в образце доминирует рассеяние на примесях, то с ростом температуры подвижность возрастает и соответственно возрастает проводимость.

Значения множителей μ_r0 и μ_i0 зависят от химического состава материала, наличия в нем дефектов и примесей, степени их ионизации (для разных образцов одного материала эти значения могут быть различными).

При одновременном действии нескольких механизмов рассеяния для расчета подвижности можно воспользоваться понятием эффективной подвижности носителей, которая будет определяться всеми, имеющими место механизмами рассеяния. Для случая, когда доминирует рассеяние на колебаниях решетки и ионизованной примеси для эффективной подвижности можно записать (считая, что акты рассеяния — независимые события):

(1.45)

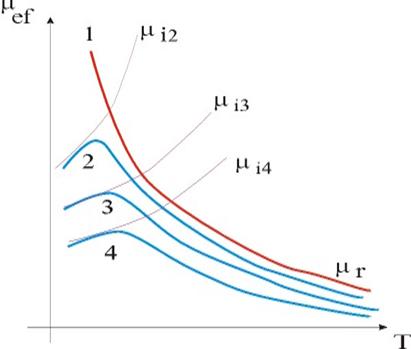
На рис. 1.21 схематически показана зависимость эффективной подвижности от температуры в полупроводниковом материале с разной концентрацией примеси. Графики построены в соответствии с формулами (1.43) и (1.45). Кривая 1 соответствует образцу без примесей. Кривые 2, 3, 4 образцам с разным содержанием примеси (большему номеру соответствует большее содержание примеси). На этом же график приведены соответствующие кривые для чисто решеточного μ_r и примесного рассеяния: μ_r2 , μ_r3, μ_r4.

Характер изменения электропроводности полупроводников с температурой, в том случае, если не изменяется концентрация носителей заряда будет определяться температурной зависимостью подвижности и зависимости будут аналогичны показанным на рис. 2 (это может быть в примесной области температурной зависимости проводимости).

Рис. 1.21. Диаграмма, поясняющая температурную зависимость подвижности μ_ef, при рассеянии на решетке μ_r и ионизированной примеси μ_iK.

Дата добавления: 2018-06-01 ; просмотров: 918 ; Мы поможем в написании вашей работы!

Источник

Как найти скорость через напряжение

Найти скорость ν электрона, прошедшего разность потенциалов U , равную 10 В

Дано:

Решение:

Закон сохранения энергии

С корость электрона

Ответ:

Решите задачу. Определить скорость, полученную электроном, если он прошел ускоряющую разность потенциалов 1,2 МэВ

По закону сохранения энергии «Работа электрического поля= кинетической энергии электрона».
А=Ек.
А=е*U. ( e -заряд электрона=1,6*10^(-19)Кл, U — разность потенциалов ( напряжение) (проверь условия разность потенциалов не может быть в эВ, она в В (вольтах) )
Ек=m*v^2 / 2. ( m -масса электрона=9,1*10^(-31)кг, v -скорость электрона. ) подставим
e*U = m*v^2 / 2. выразим скорость
v=корень квадратный из 2е*U / m.
осталось подставить и посчитать.

Чему равна скорость электрического тока? Часть 3-я

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.

© Все права принадлежат авторам, 2000-2023. Портал работает под эгидой Российского союза писателей. 18+

Найти скорость, которую приобретает электрон, пролетевший в электрическом поле

Найти скорость, которую приобретает электрон, пролетевший в электрическом поле от точки с потенциалом 100 В до точки с потенциалом 300 В, если начальная скорость электрона равна 5 Мм/с.

Задача №6.3.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

(varphi_1=100) В, (varphi_2=300) В, (upsilon_0=5) Мм/с, (upsilon-?)

Решение задачи:

alt=»Схема к решению задачи» width=»300″ height=»93″ />Работу электрического поля (A) при перемещении электрона из точки с потенциалом (varphi_1) до точки с потенциалом (varphi_2) необходимо определять по формуле:

[A = – Delta varphi e]

В этой формуле (Delta varphi) – разность потенциалов, равная (Delta varphi = <varphi _1>– <varphi _2>), (e) – модуль заряда электрона (элементарный заряд), равный 1,6·10 -19 Кл. Знак “минус” появился из-за того, что электрон имеет отрицательный заряд. Тогда:

Работа электрического поля также равна изменению кинетической энергии электрона:

Масса электрона (m) равна 9,1·10 -31 кг. Приравняем (1) и (2), тогда:

Задача решена в общем, теперь подставим в формулу численные значения и посчитаем ответ:

Ответ: 9,76·10 6 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.