Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
Мощность (N) определяют по формуле:
Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Пример:
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
N=F⋅v
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Пример:
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
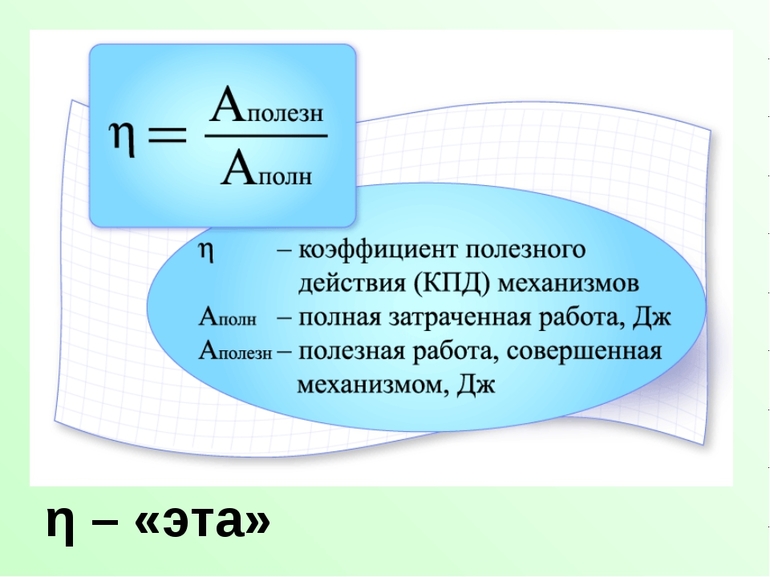
Коэффициент полезного действия обозначается буквой греческого алфавита («эта»)
η
, он является отношением полезной мощности (N) к полной или общей мощности
Nполная
.
Для его определения используют формулу:
η=NNполная
. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу:
η=NNполная⋅100%
.
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе
Aполная
. В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
Коэффициент полезного действия всегда меньше (1), или (100) % (
η
< 1, или
η
< (100) %).
|
Вот собственно и задача: Моторы электропоезда при движении со скоростью V 54 км/ч потребляют мощность N = 900 кВт. К. П. Д. моторов и передающих механизмов η= 0,8. Как найти силу тяги моторов? Сила тяги тем больше, чем больше мощность и чем меньше скорость (на подъёме мы переключаемся на меньшую скорость). Поэтому, чтобы найти силу тяги двигателя электропоезда нужно полезную мощность разделить на скорость. Находим полезную мощность, КПД умножаем на мощность 0,8*900=720 кВт, переводим скорость в км/час в м/с. V=54км/ч=15м/с. Теперь несложно найти силу тяги, 720 кВт / 15м/с =48 кн. автор вопроса выбрал этот ответ лучшим alexm12 5 лет назад В учебнике физики написано что мощность это произведение силы на скорость. Соответственно, Сила тяги моторов будет отношение мощности к скорости. Ну и на КПД все потом надо помножить. Калькулятор утверждает что сила тяги равна 48 килоньютон. Ничего сам не придумал, чесслово. Знаете ответ? |
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
КПД теплового двигателя рассчитывается по формуле $eta = frac{A_п}{Q_1}$ или $eta = frac{Q_1 — Q_2}{Q_1} cdot 100 %$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Когда говорят о коэффициенте полезного действия теплового двигателя, часто используют понятие мощности или полезной мощности: $N = frac{A_п}{t}$. Эту величину в жизни использовать удобнее, чем говорить о полезной работе.
На данном уроке мы разберем решение задач, используя формулы, приведенные выше.
Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.
Задача №1
Какая работа совершена внешними силами при обработке железной заготовки массой $300 space г$, если она нагрелась на $200 degree C$?
Дано:
$m = 300 space г$
$Delta t = 200 degree C$
$c = 460 frac{Дж}{кг cdot degree C}$
СИ:
$m = 0.3 space кг$
$A — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 — t_1) = cm Delta t$.
Рассчитаем эту энергию:
$Q = 460 frac{Дж}{кг cdot degree C} cdot 0.3 space кг cdot 200 degree C = 27 space 600 space Дж = 27.6 space кДж$.
Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 space кДж$.
Ответ: $A = 27.6 space кДж$.
Задача №2
Приняв, что вся тепловая энергия угля обращается в полезную работу, рассчитайте какого количества каменного угля в час достаточно для машины мощностью $733 space Вт$?
Дано:
$t = 1 space ч$
$N = 733 space Вт$
$q = 2.7 cdot 10^7 frac{Дж}{кг}$
СИ:
$t = 3600 space с$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Мощность по определению:
$N = frac{A_п}{t}$.
Выразим отсюда полезную работу, совершаемую машиной, и рассчитаем ее:
$A_п = Nt$,
$A_п = 733 space Вт cdot 3600 space с = 2 space 638 space 800 space Дж approx 0.26 cdot 10^7 space Дж$.
По условиям задачи количество теплоты, которое выделяется при сжигании каменного угля, равно полезной работе:
$A_п = Q = qm$.
Выразим отсюда массу угля и рассчитаем ее:
$m = frac{A_п}{q}$,
$m = frac{0.26 cdot 10^7 space Дж}{2.7 cdot 10^7 frac{Дж}{кг}} approx 0.1 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №3
Нагреватель за некоторое время отдает тепловому двигателю количество теплоты, равное $120 space кДж$. Тепловой двигатель совершает при этом полезную работу $30 space кДж$. Определите КПД теплового двигателя.
Дано:
$Q_1 = 120 space кДж$
$A_п = 30 space кДж$
СИ:
$Q_1 = 120 cdot 10^3 space Дж$
$A_п = 30 cdot 10^3 space Дж$
$eta — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Рассчитаем:
$eta = frac{30 cdot 10^3 space Дж}{120 cdot 10^3 space Дж} = 0.25$,
или в процентах $eta = 25 %$.
Ответ: $eta = 25 %$.
Задача №4
Нагреватель отдает тепловому двигателю за $30 space мин$ количество теплоты, равное $460 space МДж$, а тепловой двигатель отдает количество теплоты, равное $280 space МДж$. Определите полезную мощность двигателя.
Дано:
$t = 30 space мин$
$Q_1 = 460 space МДж$
$Q_2 = 280 space МДж$
СИ:
$t = 1800 space с$
$Q_1 = 460 cdot 10^6 space Дж$
$Q_2 = 280 cdot 10^6 space Дж$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = =frac{A_п}{Q_1} = frac{Q_1 — Q_2}{Q_1}$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.
Из этой формулы, мы можем сделать вывод, что $Q_1 — Q_2 = A_п$ — количество теплоты, которое пошло на совершение работы.
Величина работы также присутствует в определении мощности:
$N = frac{A_п}{t}$.
Когда мощность определяется полезной работой, мы называем ее полезной мощностью.
Подставим в формулу мощности определение работы из формулы для КПД и рассчитаем ее:
$N = frac{Q_1 — Q_2}{t}$,
$N = frac{460 cdot 10^6 space Дж — 280 cdot 10^6 space Дж}{1800 space с} = frac{180 cdot 10^6 space Дж}{1800 space с} = 0.1 cdot 10^6 space Вт = 100 space кВт$.
Ответ: $N = 100 space кВт$.
Задача №5
Паровой молот мощностью $367 space кВт$ получает от нагревателя в час количество теплоты, равное $6720 space МДж$. Какое количество теплоты в час получает холодильник?
Дано:
$N = 367 space кВт$
$t = 1 space ч$
$Q_1 = 6720 space МДж$
СИ:
$N = 367 cdot 10^3 space Вт$
$t = 3600 space с$
$Q_1 = 6720 cdot 10^6 space Дж$
$Q_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Полезная работа, совершенная тепловым двигателем, определяется разностью количества теплоты, отданному холодильнику, и количества теплоты, полученного от нагревателя:
$A_п = Q_1 — Q_2$.
Тогда, количество теплоты, которое получает холодильник будет равно:
$Q_2 = Q_1 — A_п$.
Совершенную работу мы можем определить через мощность:
$N = frac{A_п}{t}$,
$A_п = Nt$.
Подставим в формулу для количества теплоты, получаемого холодильником:
$Q_2 = Q_1 — Nt$.
Рассчитаем эту энергию:
$Q_2 = 6720 cdot 10^6 space Дж — 367 cdot 10^3 space Вт cdot 3600 space с = 6720 cdot 10^6 space Дж — 1321.2 cdot 10^6 space Дж = 5398.8 cdot 10^6 space Дж approx 5400 space МДж$.
Ответ: $Q_2 approx 5400 space МДж$.
Задача №6
Мопед, едущий со скоростью $20 frac{км}{ч}$, за $100 space км$ пути расходует $1 space кг$ бензина. КПД его двигателя равен $22 %$. Какова полезная мощность двигателя?
Дано:
$upsilon = 20 frac{км}{ч}$
$s = 100 space км$
$m = 1 space кг$
$eta = 22 % = 0.22$
$q = 4.6 cdot 10^7 frac{Дж}{кг}$
СИ:
$upsilon approx 5.6 frac{м}{с}$
$s = 100 cdot 10^3 space м$
$N — ?$
Показать решение и ответ
Скрыть
Решение:
Мощность по определению:
$N = frac{A_п}{t}$.
Полезную работу мы можем выразить из формулы для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Количество теплоты $Q_1$, выделившееся при сгорании бензина, мы можем найти по формуле:
$Q = qm$.
Подставим в формулу для расчета КПД:
$eta = frac{A_п}{qm}$.
Выразим отсюда полезную работу:
$A_п = eta cdot qm$.
Время, которое необходимо нам для расчета мощности, мы можем найти через перемещение и скорость:
$t = frac{s}{upsilon}$.
Подставим найденные формулы для величин $A_п$ и $t$ в формулу для расчета мощности:
$N = frac{eta cdot qm}{frac{s}{upsilon}} = frac{eta cdot qm cdot upsilon}{s}$.
Рассчитаем эту мощность:
$N = frac{0.22 cdot 4.6 cdot 10^7 frac{Дж}{кг} cdot 1 space кг cdot 5.6 frac{м}{с}}{100 cdot 10^3 space м} approx frac{5.67 cdot 10^7 space Дж cdot с}{0.01 cdot 10^7} approx 567 space Вт$.
Ответ: $N approx 567 space Вт$.
Задача №7
Определите КПД двигателя внутреннего сгорания мощностью $36.6 space кВт$, который сжигает в течение одного часа $10 space кг$ нефти.
Дано:
$N = 36.6 space кВт$
$t = 1 space ч$
$m = 10 space кг$
$q = 4.4 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 36.6 cdot 10^3 space Вт$
$t = 3600 space с$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1} cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, — это энергия, которая выделится при сгорании топлива:
$Q_1 = qm$.
Подставим эти выражения в формулу КПД и рассчитаем его:
$eta = frac{Nt}{qm} cdot 100%$,
$eta = frac{36.6 cdot 10^3 space Вт cdot 3600 space с}{4.4 cdot 10^7 frac{Дж}{кг} cdot 10 space кг} cdot 100 % = frac{13.176 cdot 10^7 space Дж}{44 cdot 10^7 space Дж} cdot 100 % approx 30 %$.
Ответ: $eta approx 30 %$.
Паровая машина мощностью $220 space кВт$ имеет КПД $15 %$. Сколько каменного угля сгорает в ее топке за $8 space ч$?
Дано:
$N = 220 space кВт$
$t = 8 space ч$
$eta = 15 % = 0.15$
$q = 2.7 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 220 cdot 10^3 space Вт$
$t = 28.8 cdot 10^3 space с$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД:
$eta = frac{A_п}{Q_1}$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании каменного угля:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac{Nt}{qm}$.
Выразим отсюда массу каменного угля:
$m = frac{Nt}{q eta}$.
Рассчитаем ее:
$m = frac{220 cdot 10^3 space Вт cdot 28.8 cdot 10^3 space с}{2.7 cdot 10^7 frac{Дж}{кг} cdot 0.15} = frac{633.6 cdot 10^7 space Дж}{0.405 cdot 10^7 frac{Дж}{кг}} approx 1564 space кг$.
Ответ: $m approx 1564 space кг$.
Задача №9
Современные паровые механизмы расходуют $12.57 space МДж$ в час на $735 space Вт$. Вычислите КПД таких механизмов.
Дано:
$Q_1 = 12.57 space МДж$
$t = 1 space ч$
$N = 735 space Вт$
СИ:
$Q_1 = 12.57 cdot 10^6 space Дж$
$t = 3600 space с$
$eta- ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1} cdot 100 %$.
Полезную работу, совершенную двигателем мы можем определить через его мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты $Q_1$, полученное от нагревателя, нам дано в условиях задачи.
Подставим выражение для полезной работы в формула для КПД и рассчитаем его:
$eta = frac{Nt}{Q_1} cdot 100 %$,
$eta = frac{735 space Вт cdot 3600 space с}{12.57 cdot 10^6 space Дж} cdot 100 % approx 21 %$.
Ответ: $eta approx 21 %$.
Задача №10
Мощность дизельного двигателя $367 space кВт$, КПД $30 %$. На сколько суток непрерывной работы хватит запаса нефти $60 space т$ такому двигателю?
Дано:
$N = 367 space кВт$
$m = 60 space т$
$eta = 30 % = 0.3$
$q = 4.4 cdot 10^7 frac{Дж}{кг}$
СИ:
$N = 367 cdot 10^3 space Вт$
$m = 60 cdot 10^3 space кг$
$t — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета КПД теплового двигателя:
$eta = frac{A_п}{Q_1}$.
Полезную работу $A_п$ мы можем выразить через мощность и время, за которое эта работа была совершена:
$A_п = Nt$.
Количество теплоты, полученное от нагревателя — это энергия, выделившаяся при сгорании нефти:
$Q_1 = qm$.
Подставим эти выражения в формулу для КПД:
$eta = frac{Nt}{qm}$.
Выразим отсюда время, за которое была совершена полезная работа:
$t = frac{qm eta}{N}$.
Рассчитаем его:
$t = frac{4.4 cdot 10^7 frac{Дж}{кг} cdot 60 cdot 10^3 space кг cdot 0.3}{367 cdot 10^3 space Вт} = frac{79.2 cdot 10^7 space Дж}{367 space Вт} approx 2.16 cdot 10^6 space с$.
Переведем в сутки. В одном дне $60 cdot 60 cdot 24 space с = 86 space 400 space с$. Тогда,
$t = frac{2.16 cdot 10^6}{86 space 400} = 25 space сут$.
Ответ: $t = 25 space сут$.
Трактовка понятия
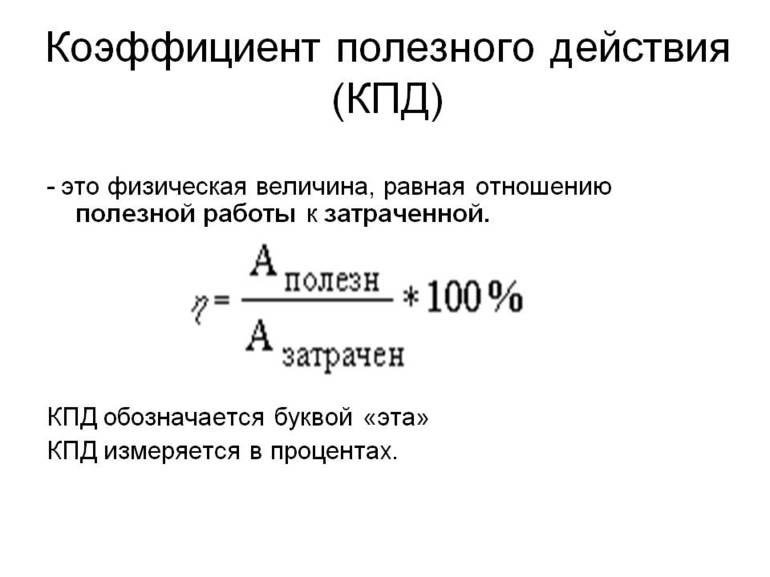
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η — обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.
Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Мощность разных устройств
По статистике, во время работы прибора теряется до 25% энергии. При функционировании двигателя внутреннего сгорания топливо сгорает частично. Небольшой процент вылетает в выхлопную трубу. При запуске бензиновый мотор греет себя и составные элементы. На потерю уходит до 35% от общей мощности.
При движении механизмов происходит трение. Для его ослабления используется смазка. Но она неспособна полностью устранить явление, поэтому затрачивается до 20% энергии. Пример на автомобиле: если расход составляет 10 литров топлива на 100 км, на движение потребуется 2 л, а остаток, равный 8 л — потеря.
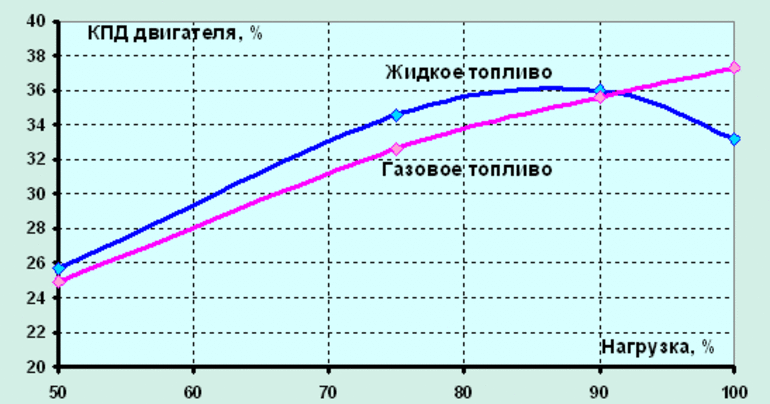
Если сравнивать КПД бензинового и дизельного моторов, полезная мощность первого механизма равна 25%, а второго — 40%. Агрегаты схожи между собой, но у них разные виды смесеобразования:
- Поршни бензинового мотора функционируют на высоких температурах, поэтому нуждаются в хорошем охлаждении. Тепло, которое могло бы перейти в механическую энергию, тратится впустую, что способствует снижению КПД.
- В цепи дизельного устройства топливо воспламеняется в процессе сжатия. На основе данного фактора можно сделать вывод, что давление в цилиндрах высокое, при этом мотор экологичнее и меньше первого аналога. Если проверить КПД при низком функционировании и большом объёме, результат превысит 50%.
Асинхронные механизмы
Расшифровка термина «асинхронность» — несовпадение по времени. Понятие используется во многих современных машинах, которые являются электрическими и способны преобразовывать соответствующую энергию в механическую. Плюсы устройств:
- простое изготовление;
- низкая цена;
- надёжность;
- незначительные эксплуатационные затраты.
Чтобы рассчитать КПД, используется уравнение η = P2 / P1. Для расчёта Р1 и Р2 применяются общие данные потери энергии в обмотках мотора. У большинства агрегатов показатель находится в пределах 80−90%. Для быстрого расчёта используется онлайн-ресурс либо личный калькулятор. Для проверки возможного КПД у мотора внешнего сгорания, который функционирует от разных источников тепла, используется силовой агрегат Стирлинга. Он представлен в виде тепловой машины с рабочим телом в виде жидкости либо газа. Вещество движется по замкнутому объёму.
Принцип его функционирования основан на постепенном нагреве и охлаждении объекта за счёт извлечения энергии из давления. Подобный механизм применяется на косметическом аппарате и современной подводной лодке. Его работоспособность наблюдается при любой температуре. Он не нуждается в дополнительной системе для запуска. Его КПД возможно расширить до 70%, в отличие от стандартного мотора.
Значения показателя
В 1824 году инженер Карно дал определение КПД идеального двигателя, когда коэффициент равен 100%. Для трактовки понятия была создана специальная машина со следующей формулой: η=(T1 — Т2)/ T1. Для расчёта максимального показателя применяется уравнение КПД макс = (T1-T2)/T1x100%. В двух примерах T1 указывает на температуру нагревателя, а T2 — температуру холодильника.
На практике для достижения 100% коэффициента потребуется приравнять температуру охладителя к нулю. Подобное явление невозможно, так как T1 выше температуры воздуха. Процедура повышения КПД источника тока либо силового агрегата считается важной технической задачей. Теоретически проблема решается путём снижения трения элементов двигателя и уменьшения теплопотери. В дизельном моторе подобное достигается турбонаддувом. В таком случае КПД возрастает до 50%.
Мощность стандартного двигателя увеличивается следующими способами:
- подключение к системе многоцилиндрового агрегата;
- применение специального топлива;
- замена некоторых деталей;
- перенос места сжигания бензина.
КПД зависит от типа и конструкции мотора. Современные учёные утверждают, что будущее за электродвигателями. На практике работа, которую совершает любое устройство, превышает полезную, так как определённая её часть выполняется против трения. Если используется подвижный блок, совершается дополнительная работа: поднимается блок с верёвкой, преодолеваются силы трения в блоке.
Решение примеров
Задача 1. Поезд на скорости 54 км/ч развивает мощность 720 кВт. Нужно вычислить силу тяги силовых агрегатов. Решение: чтобы найти мощность, используется формула N=F x v. Если перевести скорость в единицу СИ, получится 15 м/с. Подставив данные в уравнение, определяется, что F равно 48 kН.
Задача 2. Масса транспортного средства соответствует 2200 кг. Машина, поднимаясь в гору под уклоном в 0,018, проходит расстояние 100 м. Скорость развивается до 32,4 км/ч, а коэффициент трения соответствует 0,04. Нужно определить среднюю мощность авто при движении. Решение: вычисляется средняя скорость — v/2. Чтобы определить силу тяги мотора, выполняется рисунок, на котором отображаются силы, воздействующие на машину:
- тяжесть — mg;
- реакция опоры — N;
- трение — Ftr;
- тяга — F.
Первая величина вычисляется по второму закону Ньютона: mg+N+Ftr+F=ma. Для ускорения используется уравнение a=v2/2S. Если подставить последние значение и воспользоваться cos, получится средняя мощность. Так как ускорение считается постоянной величиной и равно 9,8 м/с2, поэтому v= 9 м/с. Подставив данные в первую формулу, получится: N= 9,5 kBt.
При решении сложных задач по физике рекомендуется проверить соответствие предоставленных в условиях единиц измерения с международными стандартами. Если они отличаются, необходимости перевести данные с учётом СИ.