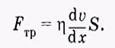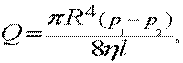Физический смысл градиента скорости:
Градиентом
любой физической величины называется
изменение этой величины, отнесённое
к расстоянию, вдоль которого это изменение
происходит.
3.
Силы внутреннего трения зависят от
природы жидкости, так как молекулы
различных жидкостей находятся на
различных расстояниях
и имеют различную скорость, а следовательно
и кинетическую энергию. Эта зависимость
учитывается коэффициентом вязкости
— η.
Таким
образом, силы внутреннего трения зависят
от природы жидкости, прямо пропорциональны
градиенту скорости и площади
соприкасающихся слоев.
Fη
= η
(dυ/dx)S
Эта
формула получила название формулы
Ньютона. Если площадь соприкасающихся
слоев S
= 1 и градиент скорости dυ/dx
= 1, то Fтр
=
η
Коэффициентом
вязкости или
вязкостью жидкости называется
величина численно равная силе трения,
возникающей между двумя слоями жидкости,
соприкасающимися на площади равной
единице и при градиенте скорости между
ними равным единице.
Коэффициент
вязкости измеряется в системе СИ: η
=Fηdx/Sdυ;
Н м / м2
(м/с) = Н с / м2
= Па с
В
системе СГС: Пуаз (Пз) = дн с / см2;
Н с / м2
= 105
дн с / 104
см2
= 10 Пз. В медицине принято измерять
вязкость в Пуазах.
Коэффициент
вязкости зависит не только от природы
жидкости, но и от температуры. С
повышением температуры коэффициент
вязкости уменьшается. Это объясняется
тем, что с повышением температуры
расстояния между молекулами увеличиваются,
а силы взаимодействия ослабляются.
Ввиду
больших трудностей, возникающих при
непосредственном измерении вязкости
её определяют косвенным путём. Наибольшее
применение имеют методы: падающего
шарика и капиллярного визкозиметра.
Метод
падающего шарика основан на законе
Стокса. Стокс установил, что на
небольшое тело шаровидной формы,
перемещающееся в жидкости, действует
сила трения, прямо пропорциональная
радиусу этого тела, его скорости и
коэффициенту вязкости жидкости.
Fтр
= 6πηrυ
Если
бросить в жидкость металлический шарик
диаметром 0,2—0,3 мм, то он будет двигаться
в жидкости равномерно. На движущийся
шарик будут действовать три силы
1.
Сила тяжести Р = mg,
направленная вертикально вниз.
2.
Выталкивающая сила FB,
направленная вертикально вверх.
3.
Сила трения FTp,
направленная также вертикально
вверх.
По
первому закону Ньютона тело двигается
равномерно, если равнодействующая всех
сил, действующих на него, равна 0.
По
закону Стокса Fтр
= 6πηrυ,
P
= mg;
m
= pTV;
P=pTVTg
=4/3 πr3pTg
Радиус
шарика можно измерить с помощью микроскопа
с окулярным микрометром, скорость
движения шарика можно определить по
формуле V
= s
/t,
измерив линейкой s,
а секундомером — t.
Метод довольно точен, используется в
санитарии. В медицинской практике для
определения коэффициента вязкости
крови, спиномозговой жидкости и других
биологических жидкостей пользуются
методом капиллярного вискозиметра,
основанный на законе Гагена-Пуазейля.
Они установили, что объём
жидкости, протекающей через поперечное
сечение капилляра (R<1мм
) в единицу времени прямо пропорционален
R4,
dP/dl
и обратно пропорционален η, коэффициент
пропорциональности в системе СИ
равен π/8.
Q=(πR4dP)/(8ηdl)
где
dP/dl
— градиент давления, dP
— разность давлений в начале и в конце
капилляра, dl
— длина капилляра. При пропускании
жидкостей через капилляры с одинаковым
радиусом при одинаковом градиенте
давления, получим:
V1/t
= πR4/8η1dl
объём 1 жидкости
V2/t
= πR4/8η2dl
объем 2 жидкости
Найдём
относительную вязкость, поделив 1
выражение на 2.
η2/η1
= V1/V2
— формула Гагена-Пуазейля.
Вискозиметр
состоит из двух пипеток — капилляров,
укреплённых на общей подставке. Один
капилляр имеет кран. Сначала втягивая
воздух заполняют капилляр (б) стандартной
жидкостью, как правило водой, до нулевого
деления, закрывают кран и затем
заполняют капилляр (а) исследуемой
жидкостью до нулевого деления. Открыв
кран, втягивают обе жидкости одновременно
так, чтобы исследуемая жидкость дошла
до деления.
Тогда
число делений трубки (б) укажет
относительную вякость. Зная η1,
определим η2
по
формуле:
η2
= η1V1
Преимущество
и недостатки этого метода:
1.
Позволяет измерять вязкость небольшого
количества .жидкости;
2.
Быстрота измерения (особенно для крови
— быстро свёртывается);
3.
Измерение вязкости непрозрачных
жидкостей.
Недостаток
— малая точность ввиду отсутствия
стандарта. Течение жидкости называется
ламинарным
или
слоистым, если поток жидкости представляет
собой совокупность слоев, перемещающихся
относительно друг друга без перемешивания.
При некоторой высокой скорости
течение становится турбулентным
(вихревым),
когда
происходит перемешивание слоев жидкости.
При
турбулентном течении жидкости возрастают
силы трения, а следовательно и работа
по преодолению сил трения. Это течение
жидкости сопровождается звуковым
феноменом.
Скорость,
при которой ламинарное течение переходит
в турбулентное называется критической
(υ кр.)
Величина
этой скорости зависит от вязкости
жидкости, радиуса трубки, плотности
жидкости и состояния внутренней
поверхности. Критическая скорость
вычисляется по формуле:
υкр
= (Rсеη)/pD
где
η — вязкость жидкости, р — плотность, D
—
диаметр трубки. Безразмерная величина
Rсе
называется числом Рейнольдса. Для
гладких трубок Rсе
= 2300, для трубок с шероховатыми
поверхностями эта величина меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Градиент скорости Калькулятор
| Search | ||
| Дом | Инженерное дело ↺ | |
| Инженерное дело | Гражданская ↺ | |
| Гражданская | Гидравлика и гидротехнические сооружения ↺ | |
| Гидравлика и гидротехнические сооружения | Свойства жидкости ↺ |
|
✖Изменение скорости — это разница между скоростями соседних слоев жидкости.ⓘ Изменение скорости [dv] |
+10% -10% |
||
|
✖Изменение расстояния — это разница между последовательными точками между соседними слоями жидкости.ⓘ Изменение расстояния [dy] |
+10% -10% |
|
✖Градиент скорости – это разница скоростей между соседними слоями жидкости.ⓘ Градиент скорости [dvdy] |
⎘ копия |
Градиент скорости Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Изменение скорости: 10 метр в секунду —> 10 метр в секунду Конверсия не требуется
Изменение расстояния: 1000 Миллиметр —> 1 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
10 Герц —>10 Цикл / сек (Проверьте преобразование здесь)
25 Свойства жидкости Калькуляторы
Градиент скорости формула
Градиент скорости = Изменение скорости/Изменение расстояния
dvdy = dv/dy
Что такое градиент скорости?
Разница в скорости между соседними слоями жидкости известна как градиент скорости и выражается как v / x, где v — разность скоростей, а x — расстояние между слоями.
Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости. Формула Пуазейля.
При течении реальной жидкости отдельные слои ее воздействуют друг на друга ссилами, касательными к слоям. Это явление называют внутренним трением или вязкостью.
dv/dx – производная, называемая градиентом скорости.
S– площадь взаимодействующих слоев
Это уравнение Ньютона. Сила внутреннего трения , действующая между слоями жилкости площадью S.ŋ— коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).
du/dx — градиента скорости (скорости сдвига)
Единицей вязкости является паскалъ-секунда (Па • с). В системе СГС вязкость выражают в пуазах (П): 1 Па • с = 10 П.
Ньютоновские и неньютоновские жидкости. Кровь как неньютоновская жидкость.
Ньютоновские жидкости – жидкости, вязкость которых не зависит от градиента скорости(т.е.вязкость постоянна).Это все низкомолекулярные в-ва в жидком состоянии, их смеси и истинные растворы в них низкомолекулярных в-в (вода, органич. жидкости, расплавл. металлы, соли и стекло при темп-ре выше темп-ры размягчения). Такие жидкости подчиняются уравнению Ньютона.
Коэффициент пропорциональности η (греческая буква «эта») называют коэффициентом внутреннего трения или динамической вязкостью. Единицей динамической вязкости (или просто вязкости) в системе СИ является
Неньютоновские жидкости – вязкость которых зависит от градиента скорости (т.е.вязкость не постоянная) Они не подчиняются уравнению Ньютона. Это жидкости, состоящие из крупных и сложных молекул, например эмульсии, суспензии, пены и кровь. Такие жидкости содержат молекулы или частицы, склонные к образованию пространственных структур.
Цельная кровь (суспензия эритроцитов в белковом растворе – плазме крови) в отличие от плазмы крови является неньютоновской жидкостью. Вязкость крови уменьшается с увеличением скорости v (или градиента скорости dv/dx) течения крови. Связано это с тем, что в неподвижной крови или при малых скоростях ее течения эритроциты склонны к агрегации (слипанию) и образуют структуры, напоминающие столбики монет («монетные столбики»), что приводит к возрастанию вязкости. При увеличении скорости движения крови «монетные столбики» разрушаются, и вязкость крови снижается. При остановке движения крови, эритроциты быстро (примерно, за 1 с) вновь собираются в «монетные столбики».
Закон Пуазейля (математическим выражением которого является формула Пуазейля) устанавливает зависимость между объемом жидкости, протекающим через трубу в единицу времени (расходом), длиной и радиусом трубы, и перепадом давления в ней
.
Q – объемная скорость, R – радиус сосуда, – динамическая вязкость, l – длина сосуда, p1 p2 – разность давлений на концах сосуда.
Вопрос 10
Методы определения вязкости крови: капиллярные, ротационные. Закон Стокса . Диагностическое значение вязкости крови
Закон Стокса
Совокупность методов измерения вязкости называют вискозиметрией, а приборы, используемые для таких целей, — вискозиметрами.
Капиллярный метод основан на формуле Пуазейля и заключается в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном’ перепаде давлений. Капиллярный вискозиметр применяется для определения вязкости.Капиллярными вискозиметрами измеряют вязкость от значений 10 -5 Па • с, свойственных газам, до значений 10 4 Па • с, характерных для консистентных смазок.
Применяются также ротационные вискозиметры, в которых жидкость находится в зазоре между двумя соосными телами, например цилиндрами. Один из цилиндров (ротор) вращается, а другой неподвижен. Вязкость измеряется по угловой скорости ротора, создающего определенный момент силы на неподвижном цилиндре, или по моменту силы, действующему на неподвижный цилиндр, при заданной угловой скорости вращения ротора.С помощью ротационных вискозиметров определяют вязкость жидкостей в интервале 1—10 5 Па • с, т. е. смазочных масел, расплавленных силикатов и металлов, высоковязких лаков и клеев, глинистых растворов и т. п.В ротационных вискозиметрах можно менять градиент скорости, задавая разные угловые скорости вращения ротора. Это позволяет измерять вязкость при разных градиентах и установить зависимость η = f(dv/dx), которая характерна для неньютоновских жидкостей.
В настоящее время в клинике для определения вязкости крови используют вискозиметр Гесса с двумя капиллярами
В вискозиметре Гесса объем крови всегда одинаков, а объем воды отсчитывают по делениям на трубке 1, поэтому непосредственно получают значение относительной вязкости крови. Для удобства втсчета сечения трубок 1 и 2 делают различными так, что, несмотря на разные объемы крови и воды, их уровни в трубках будут примерно одинаковы.
Вязкость крови человека в норме 4—5 мПа • спри патологии колеблется от 1,7 до 22,9 мПа * с, что сказывается на скорости оседания эритроцитов (СОЭ). Венозная кровь обладает несколько большей вязкостью, чем артериальная. При тяжелой физической работе увеличивается вязкость крови. Некоторые инфекционные заболевания увеличивают вязкость крови, другие же, например брюшной тиф и туберкулез, — уменьшают.
Вязкость жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости

Рассмотрим течение вязкой жидкости между двумя твердыми пластинками (рис. 7.1), из которых нижняя неподвижна, а верхняя движется со скоростью vB. Условно представим жидкость ввиде нескольких слоев 1, 2, 3 и т. д. Слой, «прилипший» ко дну, неподвижен. По мере удаления от дна (нижняя пластинка) слои жидкости имеют все большие скорости (v1
Дата добавления: 2015-06-22 ; просмотров: 1296 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.
Основные величины, характеризующие движение жидкости или газа. Линейная и объёмная скорости; соотношение между ними.
Основной характеристикой любого движения является его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах. Скорость перемещения самих частиц жидкости(или плывущих вместе с жидкостью мелких тел – например, эритроцитов в крови)обозначают υ и называют линейной скоростью. 


Q = 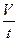

Между линейной скоростью υ и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S (см. рисунок 1).




Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x = υ·t . При этом через трубку пройдёт объём жидкости V = S·x . Объёмная скорость жидкости Q при этом будет равна 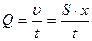

Если течение стационарно, то
Это уравнение неразрывности струи.
Течение идеальной жидкости. Теорема Бернулли.
Идеальная жидкость – жидкость несжимаемая и неимеющая силы внутреннего трения. Следовательно при движении жидкости не происходит диссипации энергии, ее полная энергия постоянна. Если жидкость движется под действием внешнего давления, то ее полная энергия есть сумма кинетической энергии, потенциальной энергии ,силы тяжести и потенциальной энергии давления. 





р – внешнее статическое давление, которое, согласно закона Паскаля, передается жидкостью во все стороны без изменения. 
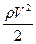


При нормальном кровообращении, как нетрудно подсчитать, динамическое давление составляет всего 1% 3% от полного. Например, в аорте линейная скорость крови около 0,7 метра в секунду, откуда
(плотность крови ≈ 1000 кг.м –3 ). Полное давление крови в аорте (среднее) около 120 мм.рт.столба. Учитывая, что 1 мм.рт.ст. = 133 паскаля, получаем, что полное давление равно 16.10 3 Па, то есть рдинамич ≈ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.
Вязкость жидкости. Закон Ньютона. Ньютоновские и неньютоновские жидкости.
В реальных жидкостях всегда существуют силы трения. Причины трения – межмолекулярные взимодействия. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трениемили вязкостью (эти термины являются синонимами).
Рассмотрим два слоя жидкости, движущиеся с разными скоростями (рис. 5). Расстояние между слоями равно х.





Выделим в каждом слое площадку с площадью S. Ньютон показал, что сила трения между этими слоями равна:

(знак „минус“ показывает, что сила трения направлена навстречу движению). Эта формула носит название формула Ньютона.
Коэффициент η (эта) называется коэффициент вязкости или просто вязкость (реже говорят „коэффициент внутреннеготрения“). F = — η grad 

Ньютоновские и неньютоновские жидкости
Для большинства жидкостей коэффициент вязкости η при постоянной температуре есть постоянная величина, зависящая только от природы жидкости и не зависящая от её скорости (точнее, от градиента скорости; см. формулу «8»). Такие жидкости принято называть „ньютоновскими“, то есть строго подчиняющимися закону Ньютона.
Однако, опыт показал, что для ряда жидкостей η ≠ const. При малых градиентах скорости(что чаще всего бывает, когда сама скорость движения жидкости мала) вязкость относительно велика, но с ростом градиента скорости вязкость уменьшается,приближаясь к некоторому, сравнительно малому постоянному значению η0.
Такие жидкости называются „неньютоновскими“ К ним относятся, во-первых, растворы веществ, молекулы которых в растворе образуют достаточно сильные межмолекулярные связи. Эти связи затрудняют перескоки молекул из одного положения в другое и тем самым снижают текучесть раствора, то есть увеличивают его вязкость. Плазма крови содержит большое количество растворённых белков, и в ней плавает большое число клеток (в основном – эритроцитов); кровь – это типичная неньютоновская жидкость. Поэтому, в частности, в капиллярах, где скорость течения крови мала, вязкость крови заметно больше, чем в крупных сосудах; это необходимо учитывать при расчётах движения крови в системе кровообращения.
источники:
http://helpiks.org/3-92163.html
http://poisk-ru.ru/s40746t13.html
Градиент скорости
Предмет
Гидравлика
Разместил
🤓 rustam.stepanov.97
👍 Проверено Автор24
интенсивность изменения скорости по заданному направлению, обычно по нормали к направлению скорости.
Научные статьи на тему «Градиент скорости»
Движение жидкостей и газов в трещиноватых и трещиновато- пористых средах
Он первым сформулировал закон, по которому скорость фильтрации прямо пропорциональна градиенту давления…
Такое поведение потока проявляется в виде отклонения связи касательного напряжения и градиента скорости…
Существует три класса неньютоновских жидкостей, напряжение в которых зависит от градиента скорости, от…
градиента скорости и времени действия напряжения, а также жидкости, где зависимость градиента скорости…
от напряжения включает в себя производные по времени напряжений и градиента скорости.

Статья от экспертов
Вязкость воды при малых градиентах скорости течения
Представлены результаты исследования вязкости воды при малых градиентах скорости течения. Показано, что с уменьшением градиента скорости течения вязкость воды увеличивается аналогично вязкости дисперсных систем, обладающих тиксотропными свойствами.
Исследование плоскорадиальной фильтрации нефти переменной вязкости
При плоскопараллельном потоке векторы скоростей параллельны по отношению к друг другу….
В каждом поперечном сечении скорость, давление, направление одинаковы, но при этом они отличаются от…
При плоскорадиальном потоке в каждой горизонтальной плоскости продолжения векторов скорости сходятся…
r • h$
где, r – радиус; h – толщина пласта;
При радиально-сферическом потоке продолжение векторов скоростей…
фильтрации нефти переменной вязкости заложены данные о характере изменения вязкости нефти, а также скорости

Статья от экспертов
Об угле гашения в растворах полимеров при больших градиентах скорости
Получена двучленная асимптотика угла гашения в сдвиговом ламинарном потоке суспензии жестких эллипсоидальных частиц при больших градиентах скорости потока. Указано условие применимости ее старшего члена. Развит метод определения размеров коллоидных частиц (макромолекул полимеров) по значениям угла гашения, измеренным при малых и больших градиентах скорости потока. Метод продемонстрирован на примере определения размеров частиц анизалдазина в растворах по экспериментальным кривым зависимости угла гашения от градиента скорости.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек