Как найти скорость маятника в нижней точке

Спрятать решение

Спрятать критерии

Классификатор: Ме­ха­ни­ка. Ме­ха­ни­че­ские ко­ле­ба­ния

1.2.13. На краю горизонтального стола
укреплен невесомый блок, через который
переброшена нить, к концам которой
привязаны одинаковые грузы ().
Полагая коэффициент трения лежащего
груза о стол равным
,
определить: 1)ускорение грузов; 2)силу
натяжения нити. Ответ:
,
.

1.2.14. На краю горизонтального стола
укреплен невесомый блок. Лежащий на
столе груз

при помощи перекинутой через блок
невесомой нити соединен с грузом
.
Стол вместе с грузами находится в лифте,
движущемся вверх с ускорением
.
Определить силу натяжения нити, если
коэффициент трения между грузом

и столом
.
Ответ:
.

1.2.15. Тело массой

движется так, что его координаты

и

изменяются со временем согласно
уравнениям:
,
,
где
,
.
Определить ускорение тела и действующую
на него силу к концу 5-й секунды после
начала движения. Ответ:
,
.

1. Законы сохранения
   в механике

   Справочные сведения

Закон сохранения импульса (для замкнутой
системы)
.

Работа переменной силы на участке
траектории 1-2
.

Кинетическая энергия
.

Потенциальная энергия тела в поле силы
тяжести
;
потенциальная энергия упруго
деформированной пружины
.

Теорема о кинетической энергии
.

Теорема о потенциальной энергии
.

Полная механическая энергия
.

Закон сохранения механической энергии
(для консервативной системы)
.

Мгновенная мощность
.

Примеры решения задач

При решении задач при помощи закона
сохранения импульса необходимо убедиться
в том, что рассматриваемая в условии
механическая система является замкнутой
или что сумма проекций сил на выбранное
направление равна нулю. После этого
следует изобразить импульсы тел
рассматриваемой системы до и после
события, о котором идет речь в условии
задачи, и выбрать систему координат.
Затем записывают закон сохранения
импульса в проекциях на оси системы
координат. В случае необходимости
следует дополнить полученную систему
уравнений кинематическими условиями,
вытекающими из связей между телами.
Если система тел не замкнута, изменение
ее импульса нужно приравнивать к импульсу
внешних сил.

При применении закона сохранения энергии
в случае замкнутой механической системы,
между телами которой действуют только
консервативные силы, необходимо
определить начальное и конечное состояния
системы и приравнять механические
энергии системы в этих состояниях. Если
система не замкнута, изменение ее
механической энергии приравнивается
к работе внешних сил. Аналогично
рассматривается задача в случае замкнутой
системы при наличии неконсервативных
сил.

Задача1. Снаряд, вылетевший из орудия
со скоростью
,
разрывается на два одинаковых осколка
в верхней точке траектории на расстоянии

от орудия (по горизонтали). Один из
осколков полетел в обратном направлении
со скоростью движения снаряда до разрыва.
Пренебрегая сопротивлением воздуха,
определите, на каком расстоянии (по
горизонтали) от орудия упадет второй
осколок, и какую скорость он будет иметь
при падении.

Решение

Определим горизонтальную скорость
снаряда в момент разрыва, для чего
воспользуемся кинематическими уравнениями
движения снаряда. Направив оси

и

по горизонтали и вертикально вниз и
совместив начало координат с орудием,
получаем

,
,
,

где

— угол бросания. В верхней точке траектории
касательная к ней направлена горизонтально,
следовательно, вертикальная проекция
скорости обращается в ноль. Отсюда
получаем время подъема снаряда до
верхней точки траектории

и расстояние, пройденное снарядом по
горизонтали до этой точки

.

По условию это расстояние равно
,
что позволяет определить угол бросания:

.

Так как горизонтальная скорость снаряда
в процессе движения не меняется, получаем

,

что приводит после несложных
тригонометрических преобразований к
формуле

.
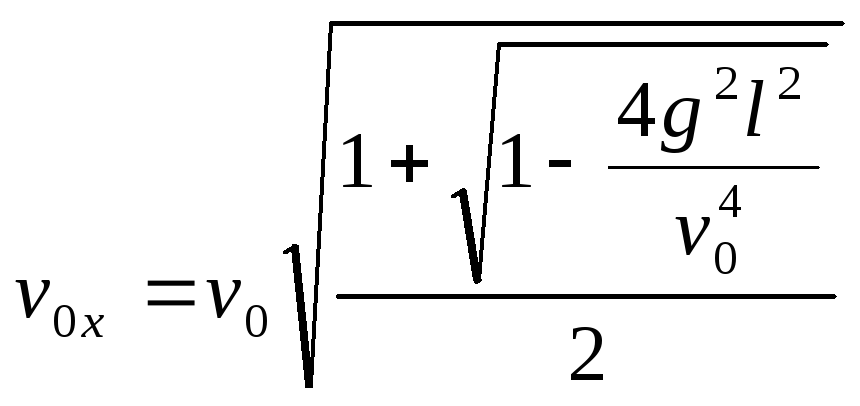
(1.3.1)

Теперь применим закон сохранения
импульса в проекции на горизонтальное
направление, согласно которому

,
(1.3.2)

где

и

— проекции скоростей осколков на
горизонтальное направление. Решая
(1.3.2) с учетом (1.3.1), находим

.

Таким образом, скорость второго осколка
в горизонтальном направлении в 3 раза
превышает горизонтальную скорость
снаряда, следовательно, учитывая, что
время падения осколка на землю совпадает
со временем подъема снаряда до верхней
точки траектории, получаем, что второй
осколок упадет на землю на расстоянии

от орудия.

Для определения скорости падения осколка
на землю найдем вертикальную скорость
снаряда в момент выстрела:

,

следовательно, по теореме Пифагора

.

Задача 2. Тело массой

поднимается без начальной скорости с
поверхности Земли под действием силы
,
изменяющейся с высотой подъема

по закону
,
где

— некоторая положительная постоянная,
и силы тяжести
.
Определить: 1) весь путь подъема; 2) работу
силы

на первой трети пути подъема. Поле силы
тяжести считать однородным.

Решение

Проектируя все силы на ось
,
по второму закону Ньютона получаем

.

По условию задачи

,
.
(1.3.3)

Таким образом, необходимо проинтегрировать
дифференциальное уравнение

(1.3.4)

с определенными выше начальными условиями
(1.3.3).

Уравнение (1.3.4) является линейным
неоднородным дифференциальным уравнением
второго порядка. Применяя стандартные
методы интегрирования таких уравнений,
находим общее решение однородного
уравнения

и очевидное частное решение неоднородного
уравнения

.

Тогда общее решение неоднородного
уравнения, равное сумме общего решения
однородного уравнения и частного решения
неоднородного уравнения, записывается
в виде

.

Для определения постоянных интегрирования
воспользуемся начальными условиями.
Из условия

находим
,
а из условия

получаем
,
откуда следует уравнение движения тела

.

Анализ полученного решения позволяет
сделать вывод, что тело совершает
колебания от поверхности Земли до
некоторой максимальной высоты, найти
которую можно из условия, что на этой
высоте скорость тела обращается в ноль.
Поскольку
,
получаем

,

откуда следует

.

Четным значениям

соответствуют моменты приземления тела
,
а нечетным – моменты поднятия тела на
максимальную высоту
.
Тогда максимальная высота подъема тела

.

Чтобы найти работу силы воспользуемся
определением

и проинтегрируем от 0 до
.
В результате получаем

.

Задача 3. Кузнечик массой

сидит на конце соломинки массой

и длиной
,
лежащей на гладкой поверхности. С какой
минимальной скоростью

должен прыгнуть кузнечик, чтобы оказаться
на другом конце соломинки?

Решение

Воспользуемся законом сохранения
импульса. До прыжка соломинка и кузнечик
находились в покое относительно земли,
следовательно, результирующий импульс
этой системы равнялся нулю. В соответствии
с законом сохранения импульса он не
может измениться после прыжка.

Если скорость соломинки после прыжка
равна
,
скорость кузнечика задана относительно
земли, а угол, который она образует с
поверхностью земли, равен
,
то закон сохранения импульса в проекции
на горизонтальное направление дает

.
(1.3.5)

Очевидно, что за время полета кузнечика
общее перемещение его и соломинки должно
равняться длине соломинки
,
следовательно,

.
(1.3.6)

Чтобы исключить из (1.3.7) время, воспользуемся
тем, что время подъема кузнечика до
верхней точки траектории равно половине
времени полета. Так как в верхней точке
вертикальная скорость обращается в
ноль, находим

.
(1.3.7)

Подставляя (1.3.7) в (1.3.6), получаем

,

что с учетом (1.3.5) дает

.

Таким образом, для скорости кузнечика
получаем выражение

.

Очевидно, скорость будет минимальной,
если
.
Тогда окончательно

.

Задача 4 Тело движется в положительном
направлении оси

под действием силы
,
где

— положительная постоянная. В момент
времени

тело находится в начале координат и его
скорость равна
.
Найти зависимость кинетической энергии
тела от координаты.

Решение

Согласно второму закону Ньютона уравнение
движения тела имеет вид

,
(1.3.8)

где
—
масса тела. Проинтегрируем это уравнение
с учетом заданных начальных условий

,
.
(1.3.9)

Данное уравнение является линейным
однородным уравнением второго порядка
и его общее решение записывается в виде

.

Из начальных условий (1.3.9) следует система
уравнений для определения произвольных
постоянных:

,
.

Решая эту систему, получаем

,
,

откуда следует

.

Тогда зависимость скорости тела от
времени принимает вид

,

а зависимость кинетической энергии от
времени

.

С учетом того, что
,
окончательно получаем

.

Задача 5. Под действием некоторой
силы тело массой

движется со скоростью
.
Найти зависимость мощности этой силы
от времени.

Решение

По определению мощность силы вычисляется
по формуле
.
Для определения силы, действующей на
тело, воспользуемся вторым законом
Ньютона

и определением ускорения
.
Вычисляя производную, находим
,
следовательно,

.

Задача 6. Однородный брусок, скользящий
по горизонтальной поверхности, попадает
на шероховатую полосу шириной

с коэффициентом трения
.
При какой скорости брусок преодолеет
эту полосу? Длина бруска
.

Решение

Воспользуемся теоремой о кинетической
энергии, согласно которой изменение
кинетической энергии равно работе силы,
действующей на тело. В данном случае
работу по торможению тела совершает
сила трения, а минимальную начальную
скорость тела определим из условия, что
после прохождения полосы брусок
останавливается.

В процессе прохождения полосы на ней
могут находиться различные по величине
части бруска, поэтому сила трения будет
меняться с течением времени. Для
вычисления работы этой переменной силы
воспользуемся следующим приемом.
Разделим мысленно брусок на бесконечно
малые пластины, большая грань которых
перпендикулярна направлению движения
бруска.

Очевидно, каждая такая пластина совершит
одинаковое перемещение по полосе, равное
длине полосы, и работа силы трения над
такой элементарной пластиной равна

,

где

— плотность вещества бруска,

— площадь его поперечного сечения.
Интегрируя по всей длине бруска, находим
результирующую работу силы трения

,

где

— масса бруска.

Изменение кинетической энергии равно

.

Применяя теорему о кинетической энергии,
получаем

,

откуда следует

.

Задача 7. Нить маятника налетает на
гвоздь, вбитый на расстоянии

под точкой подвеса. Найти максимальное
натяжение нити. Длина нити
,
начальный угол отклонения
,
масса маятника
.

Решение

Воспользуемся законом сохранения
энергии. В начальном положении маятник
поднят над нижней точкой на высоту

.

При прохождении нижнего положения
кинетическая энергия маятника
,
следовательно, по закону сохранения
энергии

,

откуда находим скорость маятника в
нижней точке

.
(1.3.10)

После того, как нить маятника налетает
на гвоздь, он начинает двигаться по
окружности радиуса
.
Применим второй закон Ньютона для того
момента, когда отрезок нити, расположенный
ниже гвоздя, составляет угол

с вертикалью.

Проектируя все силы на направление
нити, получаем

,
(1.3.11)

где

— нормальное ускорение груза.

Для этого момента по закону сохранения
энергии

.
(1.3.12)

Подставляя (1.3.10) в (1.3.12), получаем

.
(1.3.13)

Так как нормальное ускорение

,
(1.3.14)

то из (1.3.11), (1.3.13) и (1.3.14) следует

.

Очевидно, полученное выражение принимает
максимальное значение при
,
что приводит к такому ответу:

.

Задача 8. На наклонной плоскости
лежит брусок, соединенный пружиной с
неподвижной опорой. Из положения, когда
пружина не деформирована, брусок без
начальной скорости отпускают, и он
начинает скользить вниз. Определить
максимальное растяжение пружины. Масса
бруска
,
жесткость пружины
,
угол наклона плоскости к горизонту
,
коэффициент трения бруска о плоскость
.

Решение

Воспользуемся законом сохранения
энергии. В начальный момент вся энергия
системы состоит из потенциальной энергии
бруска. В момент, когда брусок
останавливается, максимально растянув
пружину, энергия системы будет состоять
из потенциальной энергии деформированной
пружины. С учетом работы, совершенной
силой трения, получаем

.
(1.3.15)

Поскольку сила трения
,
а высота опускания груза
,
подставляя эти выражения в (1.3.15), получаем

,

откуда окончательно

.

Подставляя значения, получаем

.

Задача 9. Тележка массой

стоит на гладкой горизонтальной
поверхности. На тележке укреплен
математический маятник массой

и длиной
.
В начальный момент времени система
неподвижна, а нить маятника составляет
с вертикалью угол
.
Найти скорость тележки в момент, когда
маятник будет проходить через положение
равновесия. Какова в этот момент угловая
скорость маятника?

Решение

Когда маятник начнет свое движение,
тележка по закону сохранения импульса
должна поехать навстречу ему. Применим
закон сохранения импульса в проекции
на горизонтальное направление для
момента прохождения маятником нижней
точки траектории. Если скорость маятника
относительно Земли
,
а скорость тележки
,
то по закону сохранения импульса

.
(1.3.16)

Запишем теперь закон сохранения энергии.
В начальный момент вся энергия системы
состоит из потенциальной энергии
маятника, а в момент прохождения им
нижней точки траектории она складывается
из кинетических энергий маятника и
тележки, следовательно

.
(1.3.17)

Исключая из полученных уравнений
скорость маятника, получаем

,

откуда находим

.
(1.3.18)

Для определения угловой скорости обратим
внимание на то, что вращение происходит
относительно подвижной оси, следовательно,
необходимо определить скорость маятника
относительно тележки. Так как
,
то

,

откуда для относительной скорости
получаем

.

Следовательно, угловая скорость маятника

.
(1.3.19)

Подставляя в (1.3.18), (1.3.19) числовые значения,
находим

;
.

Индивидуальные задания

1.3.1. Лодка массой

и длиной

стоит неподвижно в стоячей воде. Рыбак
массой

переходит с носа на корму лодки.
Пренебрегая сопротивлением воды,
определить, на какое расстояние при
этом сдвинется лодка. Ответ:.

Формулы математического маятника в физике

Формулы математического маятника

Определение и формулы математического маятника

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]

где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]

где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

[ {omega }_0=sqrt{frac{g}{l}}left(3right).]

Период колебаний математического маятника ($T$) в этом случае равен:

[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

[varphi =frac{x}{l}left(6right).]

Максимальное значение потенциальной энергии математического маятника равно:

[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]

Максимальная величина кинетической энергии:

[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.

Примеры задач с решением

Читать дальше: формулы пружинного маятника.