Как найти скорость отдачи винтовки

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Владельцев оружия часто интересует скорость отдачи, но они не единственные. Есть много других ситуаций, в которых полезно знать это количество. Например, баскетболист, выполняющий бросок в прыжке, может захотеть узнать свою скорость назад после того, как выпустил мяч, чтобы избежать врезаться в другого игрока, и капитан фрегата может захотеть узнать, какое влияние оказывает выпуск спасательной шлюпки на нос корабля движение. В космосе, где отсутствуют силы трения, критическая величина — скорость отдачи. Вы применяете закон сохранения количества движения, чтобы найти скорость отдачи. Этот закон выводится из законов движения Ньютона.

Закон сохранения импульса

F_I = -F_R

Второй закон Ньютона определяет силу как массовое ускорение времени. Ускорение — это изменение скорости:

a = frac { Delta v} { Delta t}

Таким образом, чистая сила может быть выражена:

F = m frac { Delta v} { Delta t}

Это позволяет переписать Третий закон так:

Это известно как закон сохранения количества движения.

Расчет скорости отдачи

В типичной ситуации отдачи выпуск тела меньшей массы (тело 1) оказывает влияние на более крупное тело (тело 2). Если оба тела стартуют из состояния покоя, закон сохранения количества движения утверждает, что m₁v₁ = -m₂v₂. Скорость отдачи обычно равна скорости тела 2 после выпуска тела 1. Эта скорость равна

v_2 = — frac {m_1} {m_2} v_1

Пример

Прежде чем решать эту проблему, необходимо выразить все величины в согласованных единицах. Одно зерно равно 64,8 мг, поэтому пуля имеет массу (м_B) 9720 мг или 9,72 грамма. Винтовка же имеет массу (м_р) 3632 грамма, так как в фунте 454 грамма. Теперь легко рассчитать скорость отдачи винтовки (v_р) в футах в секунду:

v_R = — frac {m_B} {m_R} v_B = — frac {9.72} {3,632} 2,820 = -7,55 text {фут / с}

Знак минус означает, что скорость отдачи противоположна скорости пули.

Вес выражен в одних и тех же единицах, поэтому нет необходимости в пересчете. Вы можете просто написать скорость фрегата как:

v_F = — frac {2} {2000} 15 = -0,015 text {миль / ч}

Скорость эта мала, но пренебречь ею нельзя. Это более 1 фута в минуту, что очень важно, если фрегат находится рядом с доком.

Условие задачи:

Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули, которая вылетает со скоростью 900 м/с.

Задача №2.8.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(M=500m), (upsilon=900) м/с, (u-?)

Решение задачи:

На систему тел “винтовка-пуля” вдоль оси (x) не действуют никакие силы, значит она замкнута вдоль этой оси. Применим закон сохранения импульса в проекции на эту ось:

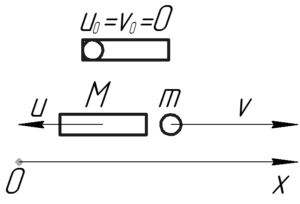
[0 =  – Mu + mupsilon ]

[u = frac{{mupsilon }}{M}]

Так как в условии сказано, что (M=500m), то:

[u = frac{{mupsilon }}{{500m}} = frac{upsilon }{{500}}]

Посчитаем численное значение скорости винтовки:

[u = frac{{900}}{{500}} = 1,8; м/с = 6,5; км/ч]

На самом деле эта задача проста только в том случае, если масса винтовки гораздо больше массы пули. Если ж их массы различаются до 10 раз, то решение становится сложным, такая задача будет скоро размещена на нашем сайте.

Ответ: 6,5 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.3 Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости

Дано:

m1 = 4 килограмма — масса винтовки;

m2 = 8 грамм = 0,008 килограмма — масса пули;

v2 = 600 метров в секунду — скорость пули.

Требуется определить скорость винтовки при отдаче v1 (метр в секунду).

Так как по условию задачи винтовка неподвижная при выстреле, что по закону сохранения импульса (количества движения):

m1 * v1 = m2 * v2, отсюда:

v1 = m2 * v2 / m1 = 0,008 * 600 / 4 = 4,8 / 4 = 1,2 метра в секунду.

Ответ: скорость винтовки при отдаче равна 1,2 метра в секунду.

Владельцы оружия часто интересуются скоростью отдачи, но они не единственные. Есть много других ситуаций, в которых полезно знать это количество. Например, баскетболист, делающий бросок в прыжке, может захотеть узнать его или ее скорость в обратном направлении после выпуска мяча, чтобы избежать столкновения с другим игроком, а капитан фрегата может захотеть узнать, какое влияние оказывает спасательная шлюпка на движение корабля вперед. В космосе, где силы трения отсутствуют, скорость отдачи является критической величиной. Вы применяете закон сохранения импульса, чтобы найти скорость отдачи. Этот закон получен из законов движения Ньютона.

TL; DR (слишком долго; не читал)

Закон сохранения импульса, полученный из законов движения Ньютона, предоставляет простое уравнение для расчета скорости отдачи. Он основан на массе и скорости выбрасываемого тела и массе откатного тела.

Закон сохранения импульса

Третий закон Ньютона гласит, что каждая приложенная сила имеет равную и противоположную реакцию. При объяснении этого закона обычно приводят пример того, как скоростной автомобиль врезался в кирпичную стену. Автомобиль прилагает усилие к стене, а стена оказывает ответное воздействие на автомобиль, который его раздавливает. Математически сила падения (F _I) равна обратной силе (F _R) и действует в обратном направлении: F _I = — F _R.

Второй закон Ньютона определяет силу как ускорение массы. Ускорение — это изменение скорости (∆v ÷ ∆t), поэтому сила может быть выражена F = m (∆v ÷ ∆t). Это позволяет переписать Третий Закон как m _I (∆v _I ÷ ∆t _I) = -m _R (∆v _R ÷ ∆t _R). В любом взаимодействии время, в течение которого прикладывается сила падения, равно времени, в течение которого применяется обратная сила, поэтому t _I = t _R, и время можно вывести из уравнения. Это оставляет:

m _I Δv _I = -m _R Δv _R

Это известно как закон сохранения импульса.

Расчет скорости отдачи

В типичной ситуации отдачи высвобождение тела меньшей массы (тело 1) оказывает влияние на тело большего размера (тело 2). Если оба тела исходят из покоя, закон сохранения импульса гласит, что m ₁ v ₁ = -m ₂ v ₂. Скорость отдачи обычно представляет собой скорость тела 2 после освобождения тела 1. Эта скорость равна

v ₂ = — (м ₁ ÷ м ₂) v ₁.

пример

• Какова скорость отдачи 8-фунтовой винтовки Винчестера после выстрела 150-гранной пули со скоростью 2820 футов в секунду?

Прежде чем решить эту проблему, необходимо выразить все величины в последовательных единицах. Одно зерно равно 64, 8 мг, поэтому масса пули (м _В) составляет 9 720 мг, или 9, 72 грамма. Винтовка, с другой стороны, имеет массу (m _R) 3632 грамма, поскольку в фунте содержится 454 грамма. Теперь легко рассчитать скорость отдачи винтовки (v _R) в футах в секунду:

v _R = — (м _B ÷ m _R) v _B = — (9, 72 г ÷ 3632 г) • 2820 фут / с = -7, 55 фут / с.

Знак минус обозначает тот факт, что скорость отдачи находится в направлении, противоположном скорости пули.

• 2000-тонный фрегат выпускает 2-тонную спасательную шлюпку со скоростью 15 миль в час. Предполагая незначительное трение, какова скорость отдачи фрегата?

Весовые коэффициенты выражаются в одних и тех же единицах, поэтому нет необходимости в конвертации. Вы можете просто записать скорость фрегата как V _F = (2 ÷ 2000) • 15 миль в час = 0, 015 миль в час. Эта скорость мала, но она ничтожна. Это более 1 фута в минуту, что важно, если фрегат находится возле дока.