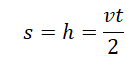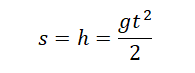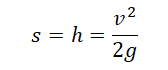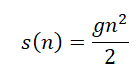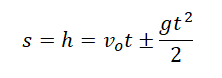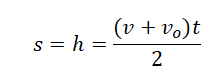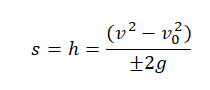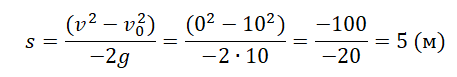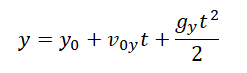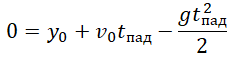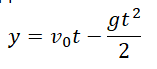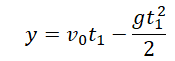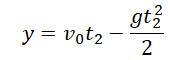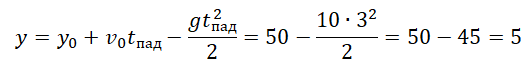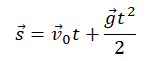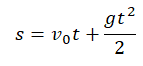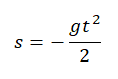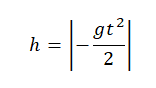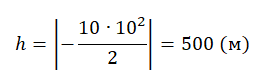Random converter
- Калькуляторы
- Механика
Калькулятор скорости, времени и расстояния при свободном падении
График зависимости скорости v (м/с) и расстояния h (м) от времени t (с) падения свободно падающего тела при нулевом сопротивлении воздуха
Этот калькулятор определяет скорость и время свободного вертикального падения тела на поверхность Земли или другой планеты, если известна высота, с которой сброшено тело. Сопротивление воздуха не учитывается. Калькулятор может также рассчитать высоту и время падения, если известна скорость, или скорость и высоту, если известно время.
Пример: Рассчитать скорость при ударе об землю тела, сброшенного с высоты 1000 м.
Ускорение свободного падения
g
или Планета
Высота
h
Время падения
t с
Скорость
v
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета введите ускорение свободного падения g или выберите планету и введите одну из трех величин h, t or v в соответствующие поля, выберите британские или метрические единицы и нажмите на кнопку Рассчитать. Будут рассчитаны две другие единицы.
Внутри спускаемого аппарата Союз ТМА-19М в экспозиции Музея науки в Лондоне
Определения и формулы
В классической механике состояние объекта, который свободно движется в гравитационном поле, называется свободным падением. Если объект падает в атмосфере, на него действует дополнительная сила сопротивления и его движение зависит не только от гравитационного ускорения, но и от его массы, поперечного сечения и других факторов. Однако на тело, падающее в вакууме, действует только одна сила, а именно сила тяжести.
Примерами свободного падения являются космические корабли и спутники на околоземной орбите, потому что на них действует единственная сила — земное притяжение. Планеты, вращающиеся вокруг Солнца, также находятся в свободном падении. Предметы, падающие на землю с небольшой скоростью, также могут считаться свободно падающими, так как в этом случае сопротивление воздуха незначительно и им можно пренебречь. Если единственной силой, действующей на предметы, является сила тяжести, а сопротивление воздуха отсутствует, ускорение одинаково для всех предметов и равно ускорению свободного падения на поверхности Земли 9,8 метров в секунду за секунду second (м/с²) или 32,2 фута в секунду за секунду (фут/ с²). На поверхности других астрономических тел ускорение свободного падения будет другим.
Командный модуль Аполлона-14 в Космическом центре им. Кеннеди, Флорида
Парашютисты, конечно, говорят, что перед раскрытием парашюта они в свободном падении, но на самом деле в свободном падении парашютист не может быть никогда, даже если парашют еще не раскрыт. Да, на парашютиста в «свободном падении» действует сила притяжения, но на него также действует противоположная сила — сопротивление воздуха, причем сила сопротивления воздуха лишь слегка меньше силы земного притяжения.
Если бы не было сопротивления воздуха, скорость тела, находящегося в свободном падении, каждую секунду увеличивалась бы на 9,8 м/с.
Скорость и расстояние свободно падающего тела вычисляется так:
где
v₀ — начальная скорость (м/с).
v — конечная вертикальная скорость (м/с).
h₀ — начальная высота (м).
h — высота падения (м).
t — время падения (с).
g — ускорение свободного падения (9,81 м/с² у поверхности Земли).
Если v₀=0 и h₀=0, имеем:
если известно время свободного падения:
если известно расстояние свободного падения:
если известна конечная скорость свободного падения:
Эти формулы и используются в данном калькуляторе свободного падения.
В свободном падении, когда нет силы для поддержания тела, возникает невесомость. Невесомость — это отсутствие внешних сил, действующих на тело со стороны пола, стула, стола и других окружающих предметов. Иными словами — сил реакции опоры. Обычно эти силы действуют в направлении, перпендикулярном поверхности соприкосновения с опорой, и чаще всего вертикально вверх. Невесомость можно сравнить с плаванием в воде, но так, что кожа воду не ощущает. Все знают это ощущение собственного веса, кода выходишь на берег после долгого купания в море. Именно поэтому для имитации невесомости при тренировках космонавтов и астронавтов используются бассейны с водой.
Само по себе гравитационное поле не может создать давление на ваше тело. Поэтому если вы находитесь в состоянии свободного падения в большом объекте (например, в самолете), который также находится в этом состоянии, на ваше тело не действуют никакие внешние силы взаимодействия тела с опорой и возникает ощущение невесомости, почти такое же, как и в воде.
Самолет для тренировок в условиях невесомости предназначен для создания кратковременной невесомости с целью тренировки космонавтов и астронавтов, а также для выполнения различных экспериментов. Такие самолеты использовались и в настоящее время эксплуатируются в нескольких странах. В течение коротких периодов времени, которые длятся около 25 секунд в течение каждой минуты полета самолет находится в состоянии невесомости, то есть для находящихся в нем людей отсутствует реакция опоры.
Для имитации невесомости использовались различные самолеты: в СССР и в Росси для этого с 1961 года использовались модифицированные серийные самолеты Ту-104АК, Ту-134ЛК, Ту-154МЛК и Ил-76МДК. В США астронавты тренировались с 1959 г. на модифицированных AJ-2, C-131, KC-135 и Boeing 727-200. В Европе Национальным центром космических исследований (CNES, Франция) для тренировок в невесомости используют самолет Airbus A310. Модификация заключается в доработке топливной, гидравлической и некоторых других систем с целью обеспечения их нормальной работы в условиях кратковременной невесомости, а также усиления крыльев для того чтобы самолет мог выдерживать повышенные ускорения (до 2G).
Несмотря на то, что иногда при описании условий свободного падения во время космического полета на орбите вокруг Земли говорят об отсутствии гравитации, конечно сила тяжести присутствует в любом космическом аппарате. Что отсутствует, так это вес, то есть сила реакции опоры на объекты, находящиеся в космическом корабле, которые движутся в пространстве с одинаковым ускорением свободного падения, которое только немного меньше, чем на Земле. Например, на околоземной орбите высотой 350 км, на которой Международная космическая станция (МКС) летает вокруг Земли, гравитационное ускорение составляет 8,8 м/с², что всего на 10% меньше, чем на поверхности Земли.
Для описания реального ускорения объекта (обычно летательного аппарата) относительно ускорения свободного падения на поверхности Земли обычно используют особый термин — перегрузка. Если вы лежите, сидите или стоите на земле, на ваше тело действует перегрузка в 1 g (то есть ее нет). Если же вы находитесь в самолете на взлете, вы испытываете перегрузку примерно в 1,5 g. Если тот же самолет выполняет координированный поворот с малым радиусом, то пассажиры, возможно, испытают перегрузку до 2 g, означающую, что их вес удвоился.
Манекен в костюме военного пилота и кислородной маске в Канадском музее авиации и космоса
Люди привыкли жить в условиях отсутствия перегрузок (1 g), поэтому любая перегрузка сильно влияет на человеческий организм. Как и в самолетах-лабораториях для создания невесомости, в которых все системы, работающие с жидкостями, должны быть модифицированы для того, чтобы они правильно работали в условиях нулевой (невесомость) и даже отрицательной перегрузки, люди также нуждаются в помощи и аналогичной «модификации», чтобы выжить в таких условиях. Нетренированный человек может потерять сознание при перегрузке 3–5 g (в зависимости от направления действия перегрузки), так как такая перегрузка достаточна для того, чтоб лишить мозг кислорода, потому что сердце не может подать в него достаточно крови. В связи с этим военные пилоты и космонавты тренируются на центрифугах в условиях высоких перегрузок, чтобы предотвратить потерю сознания при них. Для предотвращения кратковременной потери зрения и сознания, которые, по условиям работы, могут оказаться фатальными, пилоты, космонавты и астронавты надевают высотно-компенсирующие костюмы, который ограничивает отток крови от мозга во время перегрузок путем обеспечения равномерного давления на всю поверхность тела человека.
Механика
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.
История открытия явления
О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.
В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.
Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с2 (показатель для экватора) до 9,83 м/с2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.
Стандартное значение g принято считать равным 9,80665 м/с2. В физических расчетах, которые не требуют соблюдения высокой точности, значение ускорения принимают за 9,81 м/с2. Для облегчения расчетов допускается принимать значение g равным 10 м/с2.
Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.
Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.
Формулы для расчетов
Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с2).
Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.
Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2/2.
Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .
Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.
Интересные факты
Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.
В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.
В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.
В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.
Видео
Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.
Скорость, время и высота свободного падения
- Главная
- /
- Физика
- /
- Скорость, время и высота свободного падения
Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Скорость свободного падения
Если известно время падения
Ускорение свободного падения g =
Время падения
t =
Расстояние h =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Если известно расстояние (высота падения)
Ускорение свободного падения g =
Расстояние h =
Время падения
t =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Расстояние и время свободного падения
Ускорение свободного падения g =
Скорость свободного падения
V =/
Расстояние h =
0
Время падения
t =
0
Округление ответа:
Просто введите данные, и получите ответ.
Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.
Теория
Ускорение свободного падения
Ускорение свободного падения (g) — ускорение, которое придаёт падающему телу сила тяжести. У каждого небесного тела своё значение ускорения свободного падения, например, у планеты Земля оно составляет g = 9,80665 м/с².
Для небесных тел солнечной системы ускорение свободного падения имеет следующие значения:
- Земля – 9,80665 м/с²
- Луна – 1,62 м/с²
- Меркурий – 3,7 м/с²
- Венера – 8,87 м/с²
- Марс – 3,711 м/с²
- Сатурн – 10,44 м/с²
- Юпитер – 24,79 м/с²
- Нептун – 11,15 м/с²
- Уран – 8,87 м/с²
- Плутон – 0,617 м/с²
- Ио – 1,796 м/с²
- Европа – 1,315 м/с²
- Ганимед – 1,428 м/с²
- Каллисто – 1,235 м/с²
- Солнце – 274,0 м/с²
Как найти скорость свободного падения
Скорость свободного падения V можно рассчитать, зная расстояние (высоту) падения h или время падения t.
Зная время падения:
Формула
V = g⋅t
Пример
Для примера, рассчитаем с какой скоростью врежется в землю монета, брошенная из окна небоскрёба, если известно, что она упала за 5 секунд:
V = 9.8 ⋅ 5 = 49 м/с
Монетка ударилась об землю на скорости 49 м/с
Зная высоту падения:
Формула
V = √2⋅h⋅g
Пример
Для примера, определим скорость при ударе об землю ядра скинутого с 100 метровой вышки:
V = √2 ⋅ 100 ⋅ 9.8 = √1960 ≈ 44 м/с
Ядро ударится об землю на скорости 44 м/с
Время свободного падения
Время свободного падения — время, которое потребуется телу для того чтоб упасть на землю под действием силы тяжести. Чтобы рассчитать время свободного падения t необходимо знать высоту падения h или скорость в конце падения V.
Зная высоту падения:
Формула
t = √2h⁄g
Пример
Посчитаем чему будет равно время свободного падения t тела упавшего с высоты h = 100 метров:
t = √2⋅100⁄9.8 = √20.4 ≈ 4.5 с
Время свободного падения данного тела составит 4.5 секунды.
Зная скорость в конце падения:
Формула
t = V⁄g
Пример
Если тело после падения ударилось об землю со скоростью V = 50 м/с, то сколько секунд оно падало?
t = 50 ÷ 9.8 = 5.1 с
Время падения данного тела составило 5.1 секунды.
Высота свободного падения
Высота падения — высота с которой сбросили тело, численно равная расстоянию, которое пролетает тело за время падения. Чтобы рассчитать высоту падения h необходимо знать время падения t или скорость в конце падения V.
Зная время падения:
Формула
h = gt²⁄2
Пример
Для примера определим с какой высоты сбросили тело, если известно, что время его падения составило t = 5с:
h = 9.8 ⋅ 5² ÷ 2 = 122.5 м
Тело сбросили с высоты в 122.5 метров.
Зная скорость в конце падения:
Формула
h = V²⁄2g
Пример
Если тело после падения ударилось об землю со скоростью V = 60 м/с, то с какой высоты оно упало?
h = 60² ÷ 2⋅9.8 = 3600 ÷ 19.6 = 183.67 м
Тело упало с высоты в 183.67 метра.
См. также
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
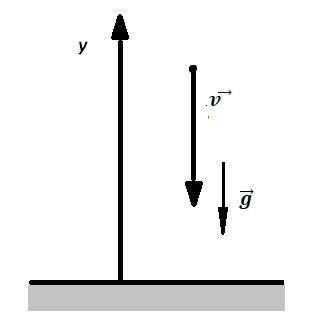
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
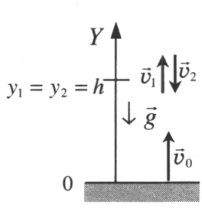
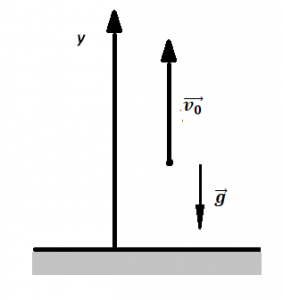
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
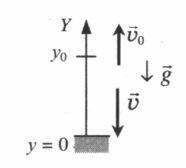
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Свободное падение на землю с некоторой высоты
Чертеж:
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
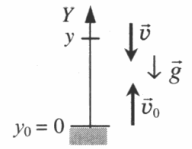
–v = v0 – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.7k
Когда объект падает с определенной высоты, сила тяжести в значительной степени влияет на его достижение. скорость. Итак, ясно, что высота — это сущность, влияющая на движение.
Свободно падающий объект сначала достигает нуля скорость, и когда он начинает двигаться вниз, он набирает скорость. Предположим, мы знаем единственную высоту падающего объекта, как найти скорость с высотой, а также вместе с высотой, как другие объекты влияют на скорость, объясняется в этом посте.
Как найти скорость по высоте?
Рассмотрим книгу, которую держат на столе на высоте h от земли. Когда книга падает со стола, скорость падения книги на землю определяется скоростью. Поскольку книга находится на высоте h, как найти скорость с высотой?
Мы знаем, что скорость можно вычислить, зная расстояние, пройденное телом, и время, затрачиваемое им на преодоление этого расстояния. Математически это можно записать как,
В приведенном выше примере нам предоставлена высота h. высота тела связана с потенциалом энергия. Таким образом, основное уравнение неверно.
Учитывая потенциальную энергию, которой обладает книга до того, как она упадет, выражение можно записать в виде
PE = мгч.
Но книга находится в движении; следовательно, потенциальная энергия теперь превращается в кинетическую энергию, как
Таким образом, потенциальная энергия и кинетическая энергия равны по закону сохранения энергии. Следовательно, уравнение можно записать в виде
Преобразовав уравнение, мы получим скорость как
v2 = 2гх
В приведенном выше уравнении g — это ускорение свободного падения. Любой объект, падающий с определенной высоты, находится под влиянием гравитации и постоянно ускоряется из-за гравитации.
Как найти скорость через ускорение и высоту?
Мы знаем, как найти скорость с ускорением и расстоянием из предыдущей статьи. Но мы дали с ускорением и высотой, тогда как найти скорость с ускорением и высотой вместо расстояния?
Ускорение и скорость пропорциональны друг другу, поскольку производная скорости по времени есть ускорение. Если у нас есть средства ускорения, при интегрировании ускорения мы можем получить скорость. Но в данном случае у нас есть ускорение и высота. Обсудим, как найти скорость с высотой, если задано ускорение.
Предположим, что мяч находится на определенной высоте над землей. Мяч падает с высоты «h», и он начинает ускоряться на «а» в направлении ускорения под действием силы тяжести; это означает, что мяч падает с высоты h в направлении силы тяжести.
Поскольку и ускорение, и ускорение свободного падения имеют одно и то же направление, общее ускорение тела равно сумме обоих ускорений тела и ускорения свободного падения A = g+a. Теперь скорость мяча можно рассчитать, используя уравнение движения.
Мы знаем из кинематического уравнения движения, что расстояние, пройденное телом, можно записать в терминах математического уравнения как
Но у нас есть высота мяча и ускорение. Расстояние можно записать через высоту как
Начальное положение мяча, когда он начинает двигаться, и конечное положение мяча определяют расстояние.
Следовательно, x = h – 0, т. е. x=h, можно сказать, что расстояние по вертикали – это высота. Теперь подставив x = h, мы получим уравнение вида
Преобразовывая приведенное выше уравнение, мы имеем
Уравнение, полученное выше, дает скорость мяча с учетом ускорения и высоты.
Приведем другой пример, если снаряд движется к земле с высоты h и его ускорение больше, чем ускорение свободного падения, так как снаряд преодолевается за счет трения о воздух, то уравнение скорости будет вычисляться как
В уравнениях кинематики скорость определяется выражением
v2 = 2Ах
Где х — расстояние. Но здесь х = h, тогда
v2 = 2Ач
Рассмотрим другой случай; если подбросить мяч в воздух, то после достижения высоты h мяч начнет ускоряться вниз под действием силы тяжести; движение называется движение снаряда; как в этой ситуации найти скорость через ускорение и высоту? Движение мяча в воздухе показано на рисунке ниже.
Из приведенного выше рисунка высота объекта равна h, а расстояние — это не высота, но у нас есть высота в терминах расстояния с использованием уравнения движения снаряда. Связь между расстоянием и высотой можно записать как
Подставив значение расстояния в уравнение движения, получим
Преобразовывая уравнение, мы получаем скорость как
Как найти начальную скорость, зная ускорение и высоту?
Начальная скорость может быть получена из ускорения и высоты, учитывая уравнение движения.
Тело ускоряется, значит, должно быть изменение скорости тела в данном случае, что также говорит о том, что изначально тело имеет некоторую скорость, которая продолжает меняться со временем. Таким образом, чтобы найти Начальная скорость, нам нужно знать конечную скорость тела.
Когда мы подбрасываем мяч в воздух, он достигает определенной высоты h с определенной скоростью и приобретает ускорение а. Изначально; мяч движется со скоростью vi. Наконец, скорость будет vf. Уравнение начальной скорости запишем с помощью уравнения движения мяча, которое можно рассчитать следующим образом.
Скорость может быть
Конечная скорость мяча определяется как vf, следовательно, из средней скорости.
Но на высоте h мяч приобретает нулевую конечную скорость, падая обратно на землю под действием силы тяжести.
Но мы не знаем, сколько времени потребуется мячу, чтобы достичь высоты h, поэтому мы можем использовать ускорение. Первоначально мяч ускоряется против силы тяжести; его ускорение станет отрицательным.
Мы знаем, конечная скорость равно нулю, то
Таким образом, мы получаем фактор времени как
Подставляя в уравнение средней начальной скорости, получаем
Преобразовывая уравнение, получаем
Мы можем вычислить начальную скорость, когда конечная скорость отлична от нуля. Рассмотрим уравнение
В приведенном выше уравнении подставив значение t как
т = (vf+vi) / а
Получаем уравнение в виде
(vf+vi) (вf-vi) = 2ah
Приведенное выше уравнение можно записать как
vf2-vi2 = 2ah
Переставляя условия, чтобы получить начальную скорость как
vi2 = Vf2— 2 часа
Как рассчитать скорость по высоте и времени?
При вертикальном движении путь, пройденный телом, равен высоте, с которой тело начинает движение.
Скорость можно рассчитать, используя высоту и время. Расстояние, пройденное телом с время всегда описывает скорость тела. Физические объекты, такие как ускорение и высота, также способствуют нахождению скорости.
Мы можем вычислить скорость по высоте и времени тремя способами.
- При вертикальном движении тела
- При метательном движении тела
- График зависимости роста от времени
При вертикальном движении тела
Если баскетбольный мяч падает из корзины на высоте h и ускоряется в направлении силы тяжести, то скорость можно определить как
Но ускорение задается
Подставляя значение a и заменяя член расстояния высотой h, мы получаем
При перестановке членов скорость с высотой и временем равна
По движению снаряда
Рассмотрим другой пример; баскетболист бросает мяч в корзину, стоящую на расстоянии d от корзины. Мяч делает движение снаряда добраться до корзины; то мы можем рассчитать скорость следующим образом:
Общее выражение скорости дается выражением
Мяч проходит расстояние d на высоте h; если пренебречь трением, расстояние можно записать как
Подставляя значение x в общее уравнение скорости, получаем
График зависимости роста от времени
Если мы построим график с высотой по оси y и временем по оси x, график называется графиком высота-время.
Мы можем рассчитать скорость по графику высота-время. Наклон графика высота-время дает скорость тела.
Из приведенного выше графика наклон определяется выражением
Из графика AB параллелен высоте h, а BC параллелен времени t; следовательно, мы можем сказать, что
АВ = h и ВС = t;
Из определения скорости мы можем сказать, что наклон есть не что иное, как скорость. Таким образом, наклон равен скорости.
Как найти скорость по высоте и массе?
Хотя масса не влияет на скорость, она вносит энергию и силу, необходимые телу для достижения определенной скорости.
Высота и масса — это объекты, связанные с объектом. потенциальная энергия. Масса также вносит вклад в кинетическую энергию, приобретаемую объектом при движении. Зная массу, давайте поймем, как найти скорость с высотой.
Объект на определенной высоте обладает потенциалом, который заставляет тело двигаться, и он равен кинетической энергии тела при движении.
Поскольку и потенциальная энергия, и кинетическая энергия равны, мы можем их приравнять.
Ep= Ek
Кинетическая энергия тела равна
Преобразовывая уравнение, получаем
В начале мы сказали, что потенциальная энергия = кинетическая энергия,
Поэтому уравнение можно переписать как
В общем случае потенциальная энергия равна Е.p= мгх.
Ответ, который мы получили из потенциальной энергии, можно подставить в приведенное выше уравнение, чтобы получить скорость тела.
Как найти скорость с учетом высоты и силы тяжести?
Когда вы бросаете камень в воздух, он падает на землю под действием силы тяжести. Это общий процесс. Но заметили ли вы, что скорость мяча? Скорость камня при движении вниз немного меньше скорости того же камня при падении назад.
Приведенное выше утверждение поясняет, что скорость может меняться и под действием силы тяжести. Гравитация вступает в действие, когда тело находится на определенной высоте; поскольку гравитация является силой притяжения, она пытается поднять тело на высоту к земле, поэтому, основываясь на этих данных, как найти скорость через высоту и расстояние?
В предыдущем разделе обсуждался один из способов нахождения скорость с высотой и силой тяжести. Обсудим, как найти скорость по высоте и расстоянию, рассматривая кинематическое уравнение движения.
Высота всегда равна расстоянию из кинематического уравнения расстояния. Следовательно, мы можем рассматривать расстояние как высоту. Таким образом, уравнение будет
Если камень движется в направлении силы тяжести, то ускорение происходит только благодаря силе тяжести; следовательно, уравнение можно переписать как
Переставив члены, уравнение будет
Приведенное выше уравнение дает скорость с высотой и силу тяжести с временным фактором. Если тело движется с ускорением против силы тяжести, то
г = -г
Как найти скорость по высоте и углу?
Когда тело начинает падать с некоторой высоты на поверхность, оно образует с точкой падения некоторый угол θ. Угол, создаваемый объектом, помогает нам найти ответ на вопрос, как найти скорость с высотой.
Компания смещение тела в вертикальном положении — высота. Вертикальную составляющую скорости можно записать как
v = v sinθ
Если тело вырабатывает некоторые горизонтальное смещение, то скорость
v = v cos θ
Из уравнения движения вертикальную и горизонтальную скорости можно записать как
vx = v cosθ
vy = v sinθ-gt; где g — ускорение свободного падения
На максимальной высоте vy= 0 = v sinθ –gt
v sinθ = gt
Когда тело падает под углом θ и движется со скоростью v, его дальность действия определяется выражением
Поэтому, используя значение R,
Следовательно, скорость можно переписать как
Решенные задачи о том, как рассчитать скорость с высотой
Задача 1) Мяч падает с высоты 15 м и достигает земли с определенной скоростью. Вычислите скорость мяча.
Решение:
Нам предоставляется только высота h = 15м.
Поскольку мяч движется к земле, движение происходит за счет ускорения силы тяжести g. Величина ускорения свободного падения g = 9.8 м/с.2. Скорость мяча
Подставляя значения h и g;
v = 17.14 м / с.
Задача 2) Вычислите начальную скорость камня, падающего с высоты 3 м, и его ускорение 2 м/с.2, и, следовательно, найти время, за которое камень достигнет земли.
Решение:
Приведенные данные: Высота h = 3м
Ускорение камня a = 2 м/с2.
Скорость камня определяется выражением
v = 3.46 м / с.
Время, необходимое камню, чтобы достичь земли, определяется уравнением
t = 1.79 с.
Задача 3) Тело массой 3 кг падает с высоты 7 м, ускоряясь под действием силы тяжести. Вычислите скорость объекта.
Решение:
Даны данные – масса объекта m = 3кг.
Высота, с которой упал предмет, h = 7 м.
Ускорение свободного падения g = 9.8 м/с.2.
Поскольку движение объекта обусловлено массой, высотой и гравитацией, то совершаемая работа равна потенциальной энергии. это дано
Ep = мгх
Объект движется, поэтому объект обладает кинетической энергией; это представлено формулой,
Из закона сохранения энергии, когда объект начинает двигаться, его потенциальная энергия теперь называется кинетической энергией.
Поэтому Еp = Ek
Потенциальная энергия Еp = 3 × 9.8 × 7
Ep = 205.8 Дж
Подставив Ep = Ek = 205.8 Дж.
v2 = 137.2
v = 11.71 м / с.
Задача 4) Спортсмен стреляет толканием ядра в воздух в вертикальном направлении, и ему требуется время 3 секунды, чтобы упасть на землю вертикально с высоты 7 м от земли. Рассчитайте скорость, с которой толкатель ядра возвращается на землю.
Решение:
Приведенные данные – высота от земли h = 7 м.
Время, необходимое для достижения земли = 3 секунды.
Скорость определяется выражением
v = 2.33 м / с.
Задача 5) Тело массой 4 кг падает с высоты 11 м над землей под углом 20°. Вычислите скорость тела. (Примите ускорение свободного падения равным 10 м/с.2)
Решение:
Приведены данные — масса тела m = 4 кг.
Высота h = 11 м.
Угол θ = 20°.
Ускорение свободного падения g = 10 м/с.2.
Скорость определяется выражением
v = 43.45 м / с.