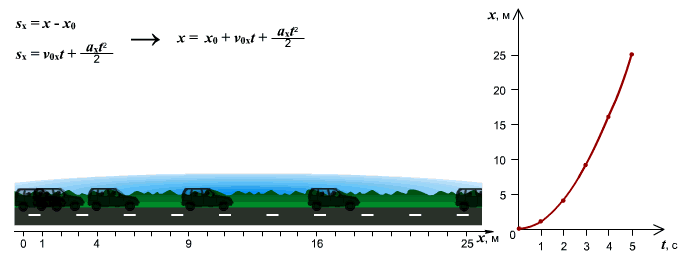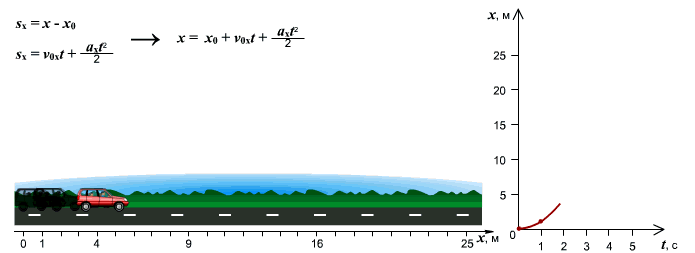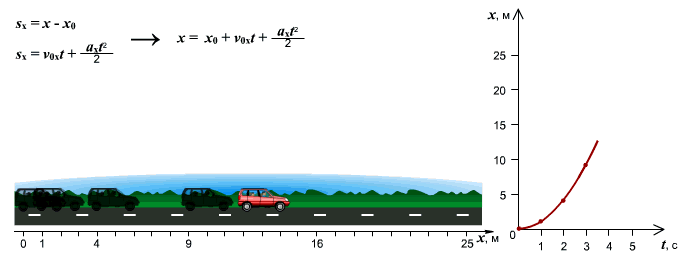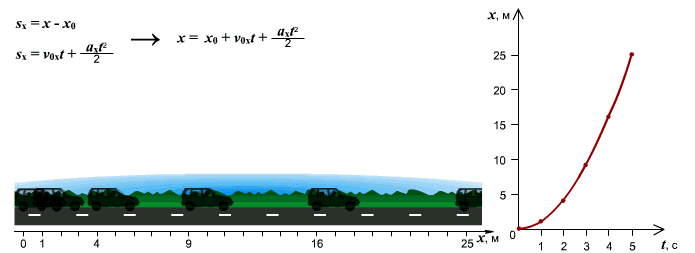
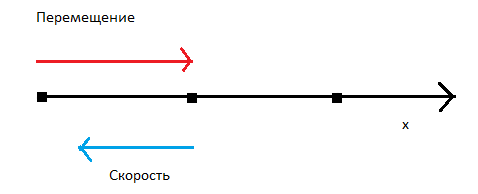
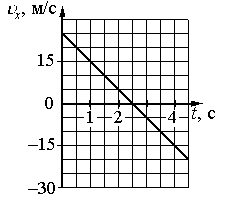Как найти скорость по графику параболы - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

движение без ускорения (равномерное), и
движение с ускорением (неравномерное).

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

Равноускоренное движение — скорость тела увеличивается.
Равнозамедленное движение — скорость уменьшается.

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

по горизонтали — время в секундах.
по вертикали — координаты тела, или проекции скорости и ускорения.

Для каждого вида движения получим три графика. Графики будем называть так:

x(t) – зависимость координаты от времени;
v(t) – зависимость проекции скорости от времени;
a(t) – зависимость проекции ускорения от времени.

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]

Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)

Скорость и ускорение неподвижного тела равны нулю:

[vec{v}=0]

[vec{a}=0]

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

Примечание: Тело движется туда, куда направлен вектор его скорости.

Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

[ x = x_{0} + v cdot t ]

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

[ v = v_{0} = const ]

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

[ a = 0 ]

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

[ v = v_{0} + a cdot t ]

Ускорение есть (рис. 4г) и оно не меняется:

[ a = const ]

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

по линейному закону, когда скорость не меняется — остается одной и той же.
по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени

Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Выводы

1). Все, что лежит:

выше оси t – положительное;
ниже оси t – отрицательное;
на горизонтальной оси t – равно нулю.

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

График x(t) координаты – это прямая линия.
График v(t) скорости – горизонтальная прямая.
График a(t) ускорения лежит на оси t.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

График x(t) координаты – это правая ветвь параболы.
График v(t) скорости – наклонная прямая.
График a(t) ускорения – горизонтальная прямая.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

График x(t) координаты – это левая ветвь параболы.
График v(t) скорости – наклонная прямая.
График a(t) ускорения – горизонтальная прямая.

Источник

График зависимости проекции скорости от времени

Зависимость проекции скорости от времени является линейной, так как описывается следующим законом:

Из курса математики нам известно похожее уравнение:

Это уравнение прямой, следовательно, график зависимости проекции скорости от времени также будет иметь вид прямой. Нарисуем эту прямую на координатной сетке (рис. 1). Для этого выбираем произвольное значение и строим произвольную прямую.

Рис. 1. График зависимости проекции скорости от времени

Проанализируем полученный график.

Видно, что скорость тела возрастала и в какой-то момент времени была равна . Это говорит о том, что проекция ускорения .

Рассмотрим прямоугольный треугольник (выделенный красным цветом). Длина катета 1 в этом треугольнике равна , а длина катета 2 равна . С помощью этих катетов найдем тангенс угла , то есть тангенс угла наклона построенной прямой:

Нам известно, что отношение изменения скорости ко времени, за которое оно произошло – это ускорение, следовательно:

Проанализируем график на рисунке 2.

Рис. 2. График зависимости проекции скорости от времени

Видно, что скорость тела не менялась и всегда оставалась равной , следовательно, проекция ускорения этого тела равно нулю . Такое движение является равномерным.

Проанализируем график на рисунке 3.

Рис. 3. График зависимости проекции скорости от времени

Видно, что проекция ускорения имеет знак минус . До момента времени модуль скорости уменьшался (тело тормозило), а далее модуль скорости увеличивался (тело разгонялось в противоположную сторону), следовательно, момент времени – это точка поворота (рис. 4).

Рис. 4. Точка поворота

Задача 1

На рисунке 5 представлен график зависимости проекции скорости от времени для движущегося тела. По данному рисунку запишите эту зависимость аналитически.

Рис. 5. Иллюстрация к задаче

Решение

Зависимость является прямой, то есть тело двигалось равноускоренно. Зависимость скорости от времени при равноускоренном движении выглядит следующим образом:

Для того чтобы записать эту зависимость для данного тела, необходимо найти проекцию начальной скорости и проекцию ускорения .

Начальная скорость – это скорость в начальный момент времени, то есть при . На данном графике видно, что начальная скорость равна (цена одного деления на оси проекции скорости ).

Формула для нахождения проекции ускорения:

Начальная скорость нам известна, а определим в произвольный момент времени. В данном случае удобно определить скорость в точке пересечения прямой с осью времени. Скорость в этой точке равна нулю . Время, за которое скорость изменилась с до определим по графику. Это время равно (цена одного деления на оси времени ).

Подставляем полученные данные в формулу проекции ускорения:

Подставляем значение проекции начальной скорости и ускорения в закон изменения проекции скорости со временем:

Ответ: .

График зависимости проекции перемещения от времени

Зависимость проекции перемещения от времени имеет следующий вид:

Множитель t в этой зависимости стоит как в первой степени, так и во второй. С точки зрения математики такая зависимость называется квадратичной, а график ее – парабола.

Рис. 6. Графики зависимости проекции перемещения от времени

На рисунке 6 изображены параболы.

Ветви параболы 1 направлены вверх, следовательно, коэффициент , то есть проекция ускорения положительная .

Для параболы 2 проекция ускорения также будет положительной . До момента времени тело двигалось в противоположную выбранной оси сторону; – точка поворота.

Ветви параболы 3 направлены вниз, следовательно, проекция ускорения меньше нуля . – точка поворота.

График зависимости координаты от времени

Зависимость координаты от времени имеет следующий вид:

Данная зависимость отличается от уравнения зависимости проекции перемещения от времени только слагаемым . Поэтому график также будет иметь вид параболы, которая сдвинута по оси ординат на величину начальной координаты () (рис. 7).

Рис. 7. Сдвиг графика

На рисунке 8 изображены графики зависимости координаты от времени.

Рис. 8. Графики зависимости координаты от времени

Парабола 1 имеет отрицательную начальную координату. Ветви этой параболы направлены вверх, следовательно, проекция ускорения будет больше нуля, .

У параболы 2 начальная координата больше нуля. Ветви этой параболы направлены вниз, следовательно, проекция ускорения будет меньше нуля, .

Модуль проекции ускорения будет больше во втором случае, так как координата (x) менялась быстрее.

Задача 2

На рисунке 9 представлен график зависимости для равноускоренно движущегося тела. Известно, что начальная координата тела составляла . По этим данным запишите аналитически зависимость , и , а также постройте график зависимости .

Рис. 9. Иллюстрация к задаче

Решение

1. Общий вид закона :

На графике видно, что проекция начальной скорости равна:

Формула для нахождения проекции ускорения:

В данном случае удобно определить скорость в точке пересечения прямой с осью времени. Скорость в этой точке равна нулю . Время, за которое скорость изменилась от начального значения до значения , определим по графику. Это время равно .

Подставляем значение проекции начальной скорости и ускорения в уравнение :

2. Общий вид закона :

Значение проекции начальной скорости и ускорения нам известны, поэтому подставляем их в уравнение:

3. Общий вид закона :

Значение проекции начальной скорости и ускорения, а также начальной координаты нам известны, поэтому подставляем их в уравнение:

4. По имеющейся зависимости построим график.

Для того чтобы построить график параболы, необходимо определить координаты вершины.

Координаты вершины параболы находятся по формулам:

;

Тогда,

Ординату вершины найдем, подставив значение абсциссы () в уравнение зависимости :

Также необходимо найти точки пересечения параболы с осями.

Из условия известна начальная координата. То есть при , . Вторую точку найдем, подставив 0 вместо в уравнение зависимости координаты от времени.

При решении данного квадратного уравнения получаем два корня и . Нам подходит положительный корень , так как мы считаем, что тело начало двигаться в момент времени . – момент времени за 2 с до начала наблюдения.

Следовательно, вторая точка имеет абсциссу , ординату .

По известным точкам строим параболу. Ветви данной параболы направлены вверх, так как в уравнении перед стоит знак плюс (рис. 10).

Рис. 10. Иллюстрация к задаче

Список литературы

М. М. Балашов, А. И. Гомонова, А. Б. Долицкий. Физика: механика. 10. – М.: Дрофа, 2004.
А. П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
В. А. Касьянов. Физика 10 кл. – М.: Дрофа, 2000.
А. В. Перышкин, В. В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «ru.solverbook.com» (Источник)
Интернет-портал «msk.edu.ua» (Источник)
Интернет-портал «festival.1september.ru» (Источник)

Домашнее задание

Задача 57, 58 (стр. 15) – А. П. Рымкевич. Физика. Задачник 10-11
Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющего одновременно двум условиям: а) средняя скорость в промежутке времени от 2 до 6 с равна 5 м/с; б) максимальная скорость в том же промежутке равна 15 м/с.
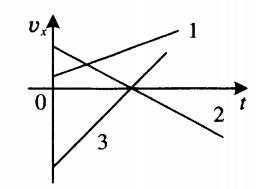
По графикам зависимости проекции скорости от времени (рис. 11) определите для каждого тела:

а) проекцию начальной скорости;

б) проекцию скорости через 2 с;

в) проекцию ускорения;

г) уравнение проекции скорости;

д) когда проекция скорости тел будет равна 6 м/с.

Рис. 11. Иллюстрация к задаче

Источник

I. Механика

Тестирование онлайн

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают

Графики равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) — прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График s(t) — наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.

График движения при . График движения при

Сравнительная таблица графиков

Источник

Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.

Что такое мгновенная скорость? Мгновенная скорость — скорость тела в данный момент времени. Обозначается v_мгн. Далее, когда мы будем говорить о скорости, мы будем понимать под ней мгновенную скорость тела и обозначать ее просто — v.

Определение

Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t₀ и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:

v = v₀+ at

v — скорость тела в данный момент времени, v₀ —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось

Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.

Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.

Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.

Скалярная формула скорости

В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:

v = v₀± at

Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.

Проекция скорости

Проекция скорости при равноускоренном прямолинейном движении имеет вид:

v_x= v_0x + a_xt

Знак проекции скорости зависит от того, в какую сторону движется тело:

Знак проекции скорости имеет знак «+», если тело движется в сторону направления оси ОХ.
Знак проекции скорости имеет знак «–», если тело движется противоположно направлению оси ОХ.

Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.

График скорости

График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.

Определение направления движения тела относительно оси ОХ по графику скорости

Если график скорости лежит выше оси времени, то тело движется в направлении оси ОХ. На рисунке этому утверждению соответствует график 1.
Если график скорости пересекает ось времени, то модуль скорости тела сначала уменьшался, и тело тормозило. Но с момента пересечения оси времени оно меняло направление движения в противоположную сторону и двигалось ускоренно. На рисунке этому соответствуют графики скорости 2 и 3.
Если график скорости лежит ниже оси времени, тело движется в направлении, противоположном направлению оси ОХ. На рисунке тело 3 до пересечения с осью времени двигалось противоположно направлению ОХ. Но тело 2 двигалось противоположно оси только после пересечения с этой осью.

Сравнение модулей ускорения по графикам скоростей

Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.

Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.

На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.

Полезные факты

Если тело начинало движение из состояния покоя, его начальная скорость равна 0, а его ускорение положительно: v₀= 0, a > 0.
Если тело заканчивает движение остановкой, то его мгновенная скорость в конечный момент времени равна 0, а его ускорение отрицательно: v = 0, a < 0.
Если тело покоится, его скорость и ускорение равны 0: v₀= 0, a = 0.

Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.

Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:

v = v₀– at

Выразим начальную скорость:

v₀ = v + at

Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

v₀ = 0 + 2 ∙ 5 = 10 (м/с)

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22

Теперь мы можем выделить кинематические характеристики движения тела:

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

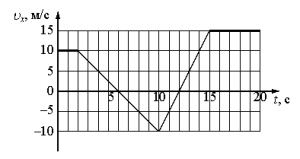
Задание EF18202

Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
Вычислить ускорение движение тела на этом участке.
Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

t₁ = 6 с. Этой точке соответствует скорость v₁ = 0 м/с.
t₂ = 10 с. Этой точке соответствует скорость v₂ = –10 м/с.

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

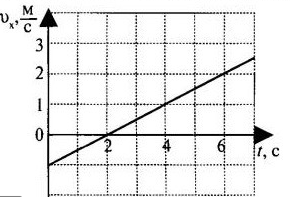
Задание EF18027

На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.

Алгоритм решения

Записать формулу ускорения.
Записать формулу для вычисления модуля ускорения.
Выбрать любые 2 точки графика.
Определить для этих точек значения времени и проекции скорости (получить исходные данные).
Подставить данные формулу и вычислить ускорение.

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

t₁ = 1 с. Этой точке соответствует скорость v₁ = 15 м/с.
t₂ = 2 с. Этой точке соответствует скорость v₂ = 5 м/с.

Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.1k

Источник

Определение кинематических характеристик движения с помощью графиков

Подробности: Обновлено 13.08.2018 21:14; Просмотров: 914

«Физика — 10 класс»

Чем отличается равномерное движение от равноускоренного?
Чем отличается график пути при равноускоренном движении от графика пути при равномерном движении?
Что называется проекцией вектора на какую-либо ось?

В случае равномерного прямолинейного движения можно определить скорость по графику зависимости координаты от времени.

Проекция скорости численно равна тангенсу угла наклона прямой x(t) к оси абсцисс. При этом, чем больше скорость, тем больше угол наклона.

Прямолинейное равноускоренное движение.

На рисунке 1.33 изображены графики зависимости проекции ускорения от времени для трёх разных значений ускорения при прямолинейном равноускоренном движении точки. Они представляют собой прямые линии, параллельные оси абсцисс: а_х = const. Графики 1 и 2 соответствуют движению, когда вектор ускорения направлен вдоль оси ОХ, график 3 — когда вектор ускорения направлен в противоположную оси ОХ сторону.

При равноускоренном движении проекция скорости зависит от времени линейно: υ_x = υ_0x + a_xt. На рисунке 1.34 представлены графики этой зависимости для указанных трёх случаев. При этом начальная скорость точки одинакова. Проанализируем этот график.

Проекция ускорения Из графика видно, что, чем больше ускорение точки, тем больше угол наклона прямой к оси t и соответственно больше тангенс угла наклона, который определяет значение ускорения.

За один и тот же промежуток времени при разных ускорениях скорость изменяется на разные значения.

При положительном значении проекции ускорения за один и тот же промежуток времени проекция скорости в случае 2 увеличивается в 2 раза быстрее, чем в случае 1. При отрицательном значении проекции ускорения на ось ОХ проекция скорости по модулю изменяется на то же значение, что и в случае 1, но скорость уменьшается.

Для случаев 1 и 3 графики зависимости модуля скорости от времени будут совпадать (рис. 1.35).

Используя график зависимости скорости от времени (рис. 1.36), найдём изменение координаты точки. Это изменение численно равно площади заштрихованной трапеции, в данном случае изменение координаты за 4 с Δx = 16 м.

Мы нашли изменение координаты. Если необходимо найти координату точки, то к найденному числу нужно прибавить её начальное значение. Пусть в начальный момент времени х₀ = 2 м, тогда значение координаты точки в заданный момент времени, равный 4 с, равно 18 м. В данном случае модуль перемещения равен пути, пройденному точкой, или изменению её координаты, т. е. 16 м.

Если движение равнозамедленное, то точка в течение выбранного интервала времени может остановиться и начать двигаться в направлении, противоположном начальному. На рисунке 1.37 показана зависимость проекции скорости от времени для такого движения. Мы видим, что в момент времени, равный 2 с, направление скорости изменяется. Изменение координаты будет численно равно алгебраической сумме площадей заштрихованных треугольников.

Вычисляя эти площади, мы видим, что изменение координаты равно -6 м, это означает, что в направлении, противоположном оси ОХ, точка прошла большее расстояние, чем по направлению этой оси.

Площадь над осью t берём со знаком «плюс», а площадь под осью t, где проекция скорости отрицательна, — со знаком «минус».

Если в начальный момент времени скорость некоторой точки была равна 2 м/с, то координата её в момент времени, равный 6 с, равна -4 м. Модуль перемещения точки в данном случае также равен 6 м — модулю изменения координаты. Однако путь, пройденный этой точкой, равен 10 м — сумме площадей заштрихованных треугольников, показанных на рисунке 1.38.

Изобразим на графике зависимость координаты х точки от времени. Согласно одной из формул (1.14) кривая зависимости координаты от времени — x(t) — парабола.

Если движение точки происходит со скоростью, график зависимости которой от времени изображён на рисунке 1.36, то ветви параболы направлены вверх, так как а_х > 0 (рис. 1.39). По этому графику мы можем определить координату точки, а также скорость в любой момент времени. Так, в момент времени, равный 4 с, координата точки равна 18 м.

Для начального момента времени, проводя касательную к кривой в точке А, определяем тангенс угла наклона α₁, который численно равен начальной скорости, т. е. 2 м/с.

Для определения скорости в точке В проведём касательную к параболе в этой точке и определим тангенс угла α₂. Он равен 6, следовательно, скорость равна 6 м/с.

График зависимости пути от времени — такая же парабола, но проведённая из начала координат (рис. 1.40). Мы видим, что путь непрерывно увеличивается со временем, движение происходит в одну сторону.

Если движение точки происходит со скоростью, график зависимости проекции которой от времени изображён на рисунке 1.37, то ветви параболы направлены вниз, так как а_x < 0 (рис. 1.41). При этом моменту времени, равному 2 с, соответствует вершина параболы. Касательная в точке В параллельна оси t, угол наклона касательной к этой оси равен нулю, и скорость также равна нулю. До этого момента времени тангенс угла наклона касательной уменьшался, но был положителен, движение точки происходило в направлении оси ОХ.

Начиная с момента времени t = 2 с, тангенс угла наклона становится отрицательным, а его модуль увеличивается, это означает, что движение точки происходит в направлении, противоположном начальному, при этом модуль скорости движения увеличивается.

Модуль перемещения равен модулю разности координат точки в конечный и начальный моменты времени и равен 6 м.

График зависимости пройденного точкой пути от времени, показанный на рисунке 1.42 отличается от графика зависимости перемещения от времени (см. рис. 1.41).

Как бы ни была направлена скорость, путь, пройденный точкой, непрерывно увеличивается.

Выведем зависимость координаты точки от проекции скорости. Скорость υx = υ_0x + a_xt, отсюда

В случае x₀ = 0, а_х > 0 и υ_x > υ_0x график зависимости координаты от скорости представляет собой параболу (рис. 1.43).

При этом, чем больше ускорение, тем ветвь параболы будет менее крутой. Это легко объяснить, так как, чем больше ускорение, тем меньше расстояние, которое должна пройти точка, чтобы скорость увеличилась на то же значение, что и при движении с меньшим ускорением.

В случае а_х < 0 и υ_0x > 0 проекция скорости будет уменьшаться. Перепишем уравнение (1.17) в виде где а = |а_x|. График этой зависимостимости — парабола с ветвями, направленными вниз (рис. 1.44).

Ускоренное движение.

По графикам зависимости проекции скорости от времени можно определить координату и проекцию ускорения точки в любой момент времени при любом типе движения.

Пусть проекция скорости точки зависит от времени так, как показано на рисунке 1.45. Очевидно, что в промежутке времени от 0 до t₃ движение точки вдоль оси X происходило с переменным ускорением. Начиная с момента времени, равного t₃, движение равномерное с постоянной скоростью υ_Dx. По графику мы видим, что ускорение, с которым двигалась точка, непрерывно уменьшалось (сравните угол наклона касательной в точках В и С).

Изменение координаты х точки за время t₁ численно равно площади криволинейной трапеции OABt₁, за время t₂ — площади OACt₂ и т. д. Как видим по графику зависимости проекции скорости от времени можно определить изменение координаты тела за любой промежуток времени.

По графику зависимости координаты от времени можно определить значение скорости в любой момент времени, вычисляя тангенс угла наклона касательной к кривой в точке, соответствующей данному моменту времени. Из рисунка 1.46 следует, что в момент времени t₁ проекция скорости положительна. В промежутке времени от t₂ до t₃ скорость равна нулю, тело неподвижно. В момент времени t₄ скорость также равна нулю (касательная к кривой в точке D параллельна оси абсцисс). Затем проекция скорости становится отрицательной, направление движения точки изменяется на противоположное.

Если известен график зависимости проекции скорости от времени, можно определить ускорение точки, а также, зная начальное положение, определить координату тела в любой момент времени, т. е. решить основную задачу кинематики. По графику зависимости координаты от времени можно определить одну из самых важных кинематических характеристик движения — скорость. Кроме этого, по указанным графикам можно определить тип движения вдоль выбранной оси: равномерное, с постоянным ускорением или движение с переменным ускорением.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»

Источник