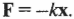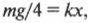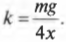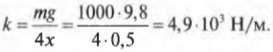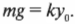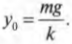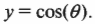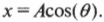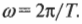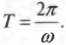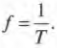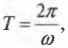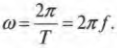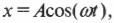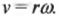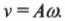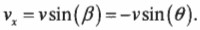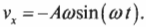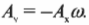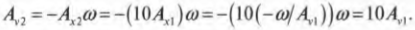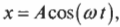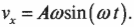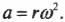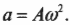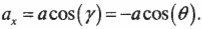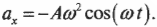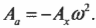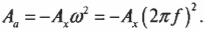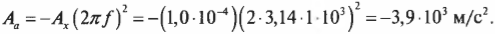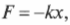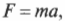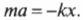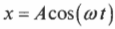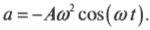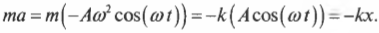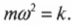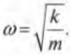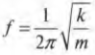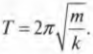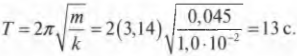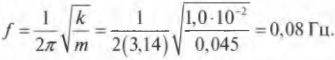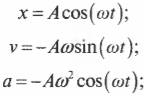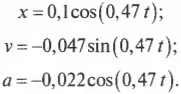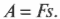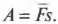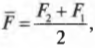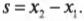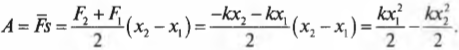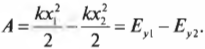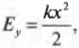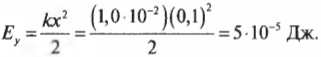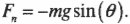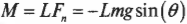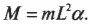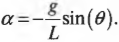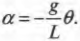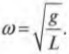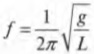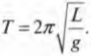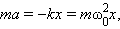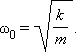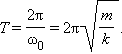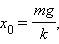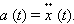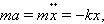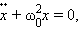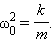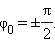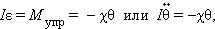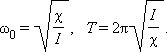Как найти скорость по растяжению пружины

В этой главе …

• Изучаем закон Гука
• Осваиваем основы простого гармонического движения
• Изучаем особенности простого гармонического движения
• Измеряем энергию простого гармонического движения
• Вычисляем период колебаний маятника

Эта глава посвящена описанию еще одного типа движения, а именно: описанию периодического движения. Примерами такого движения являются колебания грузика на пружинке, качания маятника и даже прыжки с высоты с помощью эластичной веревки. В этой главе рассматриваются закономерности и особенности таких повторяющихся, т.е. периодических движений. Здесь мы научимся вычислять характеристики периодического движения: период колебаний пружинки и маятника, упругую энергию сжатой пружины и т.д.

Постигаем закон Гука

Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.

Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину ​( x )​, потребуется приложить внешнюю силу ​( F_{вн} )​, которая равна:

где ​( k )​ — это коэффициент пропорциональности.

Точнее говоря, вектор деформации ​( mathbf{x} )​ всегда направлен противоположно силе сопротивления пружины (или силе упругости) ( mathbf{F} ), а потому в векторную формулировку закона Гука обычно входит знак “минус”:

Растягиваем и сжимаем пружины

Следует помнить, что закон Гука относится только к упруго деформируемым материалам.

В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности ​( k )​ в законе Гука ​( F=kx )​ называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.

Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?

Вес автомобиля равен ​( mg )​, где ​( g )​ — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка ​( mg/4 )​.

Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:

т.е. коэффициент упругости равен:

Подставляя значения, получим:

Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·10³ Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.

Изучаем особенности закона Гука

Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:

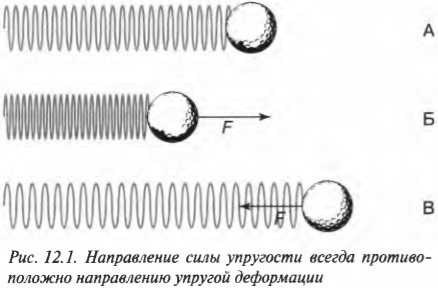
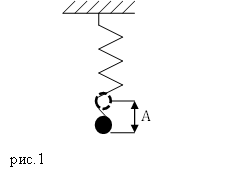
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.

Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).

Сила упругости пружины не зря называется силой сопротивления, ведь она стремится установить равновесие.

Движется дальше: простое гармоническое движение

Простым гармоническим движением называется такое движение, при котором сила сопротивления движению пропорциональна перемещению. При этом сила трения не учитывается, и никакие другие внешние силы не оказывают никакого влияния на движение. Такое движение будет выполняться периодически и бесконечно долго. Конечно же, в реальной ситуации так не бывает, но здесь имеется в виду именно идеализированная ситуация.

Изучаем простое гармоническое движение по горизонтали и по вертикали

На рис. 12.1 показан пример движения мячика, прикрепленного к пружине. При сжатии пружины внешней силой справа налево в пружине возникает сила упругости, которая стремится вернуть мячик в исходное положение. После возврата мячика в исходное положение он останавливается не сразу, а спустя какое-то время. Оно необходимо для торможения ускорившегося мячика с помощью силы упругости, возникающей при растягивании вправо. Дело в том, что мячик обладает некоторой массой, и инерция (см. главу 11) не позволяет ему остановиться мгновенно. В результате имеем следующую последовательность событий (см. рис. 12.1).

• Схема А. Мячик находится в состоянии равновесия. Никакие силы не действуют на него. Пружина находится в нерастянутом и в несжатом состоянии.
• Схема Б. Внешняя сила сжала пружину справа налево. В пружине возникла упругая сила сопротивления ​( F )​.
• Схема В. Внешняя сила отпускает пружину (и далее не участвует в процессе движения). Упругая сила сопротивления пружины ​( F )​ стремится распрямить пружину, т.е. вернуть мячик в исходное состояние. Мячик начинает ускоренное движение.

Когда мячик проходит точку исходного положения, его скорость становится очень большой (фактически максимальной) и он продолжает движение вправо. При этом возникает деформация растяжения и соответственно направленная противоположно упругая сила сопротивления пружины. Именно так и происходит при повторяющихся движениях мячика слева направо и, наоборот, справа налево. После первоначального толчка из неподвижного состояния мячик начинает совершать периодические колебания из самого крайнего левого положения в самое крайнее правое положение.

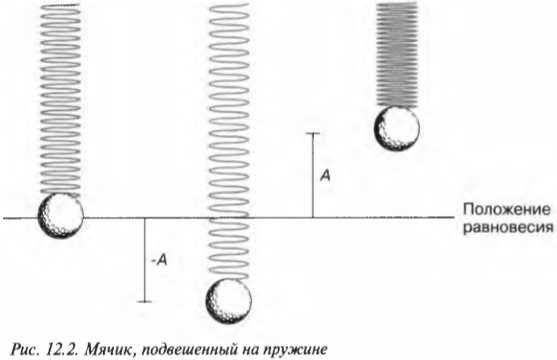
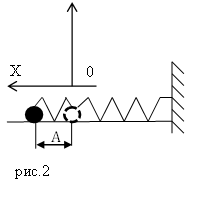
В примере на рис. 12.1 предполагается, что силы трения нет. А что будет, если пружинку с мячиком подвесить вертикально, как показано на рис. 12.2?

В подвешенном состоянии изменится положение равновесия, но после воздействия внешней силы мячик будет совершать аналогичные периодические движения, но теперь уже вверх-вниз.

Это новое равновесное положение определяется равенством веса мячика ​( mg )​ и силы упругости ​( ky_0 )​ растянутой пружины под действием этого веса:

Итак, новое положение исходного равновесия будет определяться формулой:

Теперь если потянуть мячик вниз с помощью внешней силы и отпустить мячик, то он начнет совершать периодическое движение, как и в прежнем примере (см. рис. 12.1), но теперь уже относительно нового положения равновесия.

Периодическое движение подобного рода называется периодическим колебанием, а крайние положения мячика при таком периодическом движении мячика называются амплитудами периодических колебаний. Амплитуда является важным элементом математического описания простого гармонического движения.

Изучаем свойства простого гармонического движения

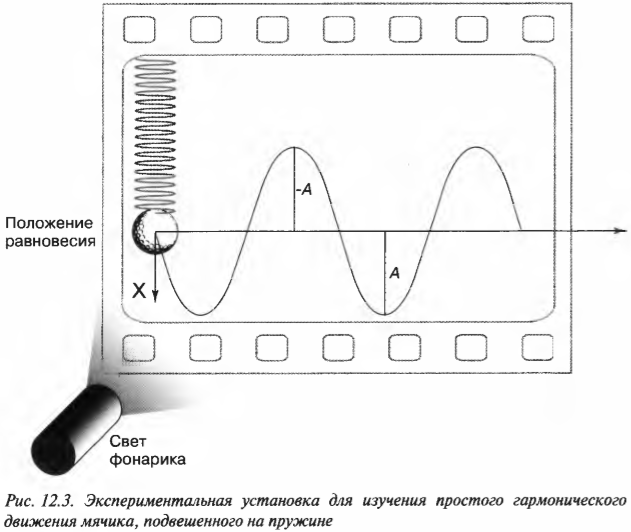
Представьте себе, что для изучения простого гармонического движения ученые решили освещенный фонариком мячик из предыдущего примера заснять на движущуюся по горизонтали фотопленку.

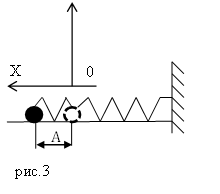
После проявки фотопленки на ней оказался четкий волнообразный след, который показан на рис. 12.3.

Оказывается, мячик действительно совершает периодические движения вверх-вниз относительно исходного равновесного положения с амплитудой А. Вблизи точки равновесия скорость мячика максимальна, а в точках амплитуды минимальна.

Траектория мячика очень похожа на синусоидальную кривую, т.е. след мячика на движущейся фотопленке описывается графиком функции ​( sin )​ (“синус”) либо ​( cos )​ (“косинус”) со сдвигом от начала координат. Действительно, решением уравнения простого гармонического движения является функция ​( sin )​ или ​( cos )​.

Изучаем траекторию простого гармонического движения

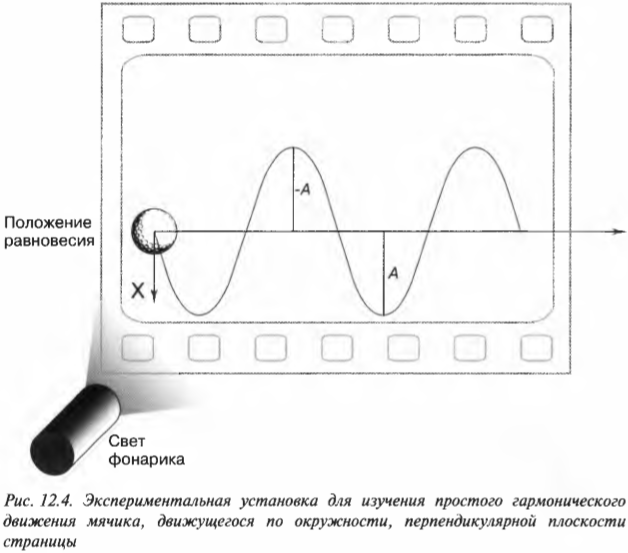
Построим и рассмотрим внимательно кривую функции:

Наверняка эта функция и ее графическое представление в виде синусоидальной кривой уже знакомо многим читателям этой книги из курса математики. Ее часто можно встретить на экранах разных приборов в реальной жизни или даже в виртуальном мире кино и компьютерных игр.

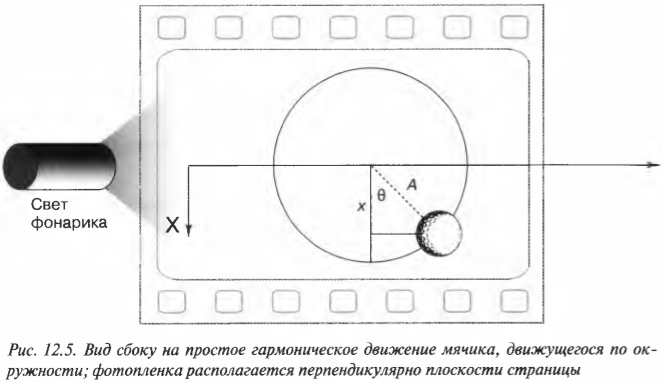
Пусть освещенный фонариком мячик движется по окружности перпендикулярной плоскости страницы и снимается на движущуюся по горизонтали фотопленку. Тогда после проявки фотопленки на ней снова появится синусоидальная кривая, как показано на рис. 12.4.

Если расположить окружность так, чтобы она была параллельна плоскости страницы (рис. 12.5), то можно легко заметить, что положение мячика определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( theta )​ — это угол поворота мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

Если мячик вращается по окружности с постоянной угловой скоростью, то ​( theta=omega t )​ и ​( x=Acos(omega t) )​.

Определяем период простого гармонического движения

Прохождение мячиком пути, равного длине окружности, называется циклом, а время его прохождения — периодом. Период обозначается символом ​( T )​ и измеряется в секундах.

На рис. 12.4 и 12.5 полный цикл соответствует движению мячика от исходного положения с амплитудой ​( A )​, затем к положению с амплитудой ​( -A )​, а потом снова к положению с амплитудой ( A ).

Как связан период с уже знакомыми нам параметрами движения? За один цикл мячик проходит угол величиной ​( 2pi )​ за период ​( T )​, т.е. его угловая скорость равна:

Откуда получаем выражение для периода:

Для характеристики периодического движения часто используют понятие частота, которое равно количеству циклов за единицу времени. Например, если мячик на рис. 12.4 совершает 1000 полных оборотов в секунду, то его частота равна 1000 с^-1. В системе СИ частоту измеряют в герцах (или сокращенно Гц), т.е. 1 с^-1 = 1 Гц. Таким образом, частота вращения мячика по окружности равна 1000 Гц.

Частота ​( f )​ и период ​( T )​ связаны очень простым соотношением:

Поскольку:

то теперь можно легко найти связь между частотой и угловой скоростью:

При описании периодических движений угловую скорость ​( omega )​ часто называют циклической частотой.

Определяем скорость в простом гармоническом движении

На рис. 12.5 мячик совершает движение по окружности, а координата перемещения по оси X определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( omega )​ — это угловая скорость мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

В любой точке с координатой х мячик обладает некоторой скоростью, которая зависит от времени. Как выразить ее с помощью математической формулы?

Очень просто, ведь для этого достаточно вспомнить о связи между угловой ​( omega )​ и тангенциальной ​( v )​ скоростью (см. главу 10):

Поскольку в данном случае ​( r=A )​, то в итоге получим для тангенциальной скорости:

Теперь для определения скорости периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию тангенциальной скорости на ось X:

(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ​( beta )​ между вектором скорости и осью X равен ​( 180^circ+theta )​, a ​( sin(beta)=sin(180^circ+theta )=-sin(theta) )​. — Примеч. ред.)

После подстановки выражений для ​( theta=omega t )​ и для ​( v=Aomega )​ получим:

Обратите внимание, что скорость меняется от исходного положения с амплитудой перемещения ​( A )​ и амплитудой скорости ​( 0 )​, затем к положению с амплитудой перемещения ​( 0 )​ и амплитудой скорости ​( -Aomega )​, потом к положению с амплитудой перемещения ​( -A )​ и амплитудой скорости ​( 0 )​, затем к положению с амплитудой перемещения ​( 0 )​ и амплитудой скорости ​( Aomega )​, а потом снова к положению с амплитудой перемещения ​( A )​ и амплитудой скорости ​( 0 )​.

Как видите, в простом гармоническом движении амплитуда скорости ​( A_v=Aomega )​ связана с амплитудой перемещения ​( A_х=A )​ формулой:

Рассмотрим следующий простой пример. Представьте себе, что несколько отчаянных парней и девушек прыгают с высоты с помощью эластичной веревки. Известно, что при прыжке с некоторой высоты относительно точки равновесия максимальная скорость в точке равновесия одного из смельчаков достигает величины 4 м/с. Он решает в 10 раз увеличить высоту прыжка. Какой будет его максимальная скорость в точке равновесия?

Итак, амплитуда скорости в первом прыжке ​( A_{v1}=-A_{х1}omega )​ равна 4 м/с. Амплитуда перемещения во втором прыжке (с новой высоты) в 10 раз больше амплитуды перемещения в начале, т.е. ​( A_{х2}=10A_{х1} )​. Вопрос: чему равна амплитуда скорости ( A_{v2}=-A_{х2}omega ) во втором прыжке? Подставляя выражение для ( A_{х2}=-omega/A_{v1} ) в формулу ( A_{х2}=10A_{х1} ), а затем в формулу ( A_{v2}=-A_{х2}omega ), получим:

Итак, при увеличении амплитуды прыжка в 10 раз амплитуда скорости возрастает тоже в 10 раз, т.е. становится равной 40 м/с.

Определяем ускорение в простом гармоническом движении

Вернемся к примеру на рис. 12.5, где мячик совершает движение по окружности. Его координата перемещения по оси X определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( omega )​ — это угловая скорость мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

Как мы уже выяснили в предыдущем разделе, его скорость перемещения по оси X определяется формулой:

Однако вращательное движение мячика также характеризуется центростремительным ускорением. Как выразить ее с помощью математической формулы?

Как известно (см. главу 10), угловая скорость ​( omega )​ центростремительное ускорение ​( a )​ связаны следующей формулой:

Поскольку в данном случае ​( r=A )​, то в итоге получим для центростремительного ускорения:

Теперь для определения ускорения периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию центростремительного ускорения на ось X:

(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ​( gamma )​ между вектором центростремительного ускорения и осью X равен ​( 180^circ + theta )​, a ​( cos(gamma)=cos(180^circ + theta)=-cos(theta) )​. — Примеч. ред.)

После подстановки выражений для ​( theta=omega t )​ и для ​( a=Aomega^2 )​ получим:

Как видите, в простом гармоническом движении амплитуда ускорения ​( A_а=Aomega^2 )​ связана с амплитудой перемещения ​( A_х=A )​ формулой:

Рассмотрим еще один простой пример. Пусть диафрагма (тоненькая пластинка) в трубке домашнего телефона совершает простое гармоническое движение с частотой ​( theta=omega t )​ величиной 1 кГц (т.е. 1000 Гц) и амплитудой перемещения ( A_х=A ) величиной 1,0·10^-4 м. Чему равна амплитуда ускорения мембраны ​( A_а )​?

Поскольку ​( omega=2pi!f )​, то после подстановки этого выражения в предыдущую формулу ( A_а=-A_хomega^2 ) получим:

Подставляя численные значения, получим:

Как видите, мембрана обычного телефона испытывает очень большое ускорение, которое почти в 400 раз больше ускорения свободного падения ​( g )​ = 9,8 м/с² под действием гравитационного притяжения Земли.

Определяем частоту колебаний груза на пружине

С математической точки зрения колебания груза на пружине и движение мячика по окружности (см. предыдущие разделы этой главы) принципиально не отличаются. Дело в том, что оба эти движения являются простыми гармоничными. Поэтому их основные характеристики (например, скорость, ускорение, частота и период колебаний) должны описываться аналогичными математическими формулами. Остановимся и подробно проследим за этой аналогией.

Как известно, согласно закону Гука (см. выше в этой главе), при растяжении пружины на величину ​( x )​ возникает упругая сила ​( F )​, которая равна:

где ​( k )​ — это коэффициент пропорциональности.

Согласно закону Ньютона (см. главу 5), сила и вызванное ею ускорение ​( a )​ связаны следующим соотношением:

откуда получаем:

Из предыдущего раздела нам уже известно, что в простом гармоническом движении перемещение и ускорение выражаются следующими формулами:

и

Подставляя эти выражения в предыдущую формулу, полученную на основе законов Гука и Ньютона, получим:

Сокращая некоторые переменные, получим:

Откуда легко можно выразить циклическую частоту:

Поскольку ​( omega=2pi!f )​ и ( omega=2pi/T )​, то после подстановки предыдущего выражения в эти формулы получим:

и

Пусть пружина на рис. 12.1 обладает коэффициентом упругости ​( k )​, равным 1,0·10^-2 Н/м, а к ней прикреплен груз массой 4 г. Чему будет равен период колебаний груза на пружине? Подставляя значения в предыдущую формулу для периода, получим:

А какова частота этих колебаний? Снова подставляя значения в предыдущую формулу для частоты, получим:

Используя формулы перемещения, скорости и ускорения для простого гармонического движения (см. ранее в этой главе):

можно вычислить координату, скорость и ускорение груза на пружине в произвольный момент времени. Как будут выглядеть эти формулы для задачи с грузиком на пружине?

Сначала вычислим циклическую частоту:

Если амплитуда ​( A )​ равна 10 см, то получим:

Вычисляем энергию простого гармонического движения

В простом гармоническом движении периодически происходит увеличение и уменьшение кинетической энергии, например груза на пружине. Ясно, что кинетическая энергия груза не пропадает, а преобразуется в энергию сжатой или растянутой пружины. Эта энергия называется упругой потенциальной энергией пружины. Сколько энергии запасено в сжатой или растянутой пружине?

Попробуем вычислить ее с помощью простых соображений. Как известно, работа ​( A )​ силы ​( F )​ при перемещении на расстояние ​( s )​ равна:

При сжатии или растяжении пружины сила ​( F )​ меняется линейно с расстоянием, поэтому работу этой силы по сжатию или растяжению пружины на расстояние ( s ) можно представить как произведение средней силы ​( overline{F} )​ на перемещение ( s ):

Средняя ( overline{F} ) сила определяется как:

где ​( F_1=-kx_1 )​ — это сила упругости в точке с координатой ​( x_1 )​, a ( F_2=-kx_2 ) — сила упругости в точке с координатой ( x_2 )​. При этом перемещение ​( s )​ будет равно:

Подставляя выражения для ( s ) и ( overline{F} ) в формулу работы, получим:

Члены ​( frac{kx^2_1}{2} )​ и ( frac{kx^2_2}{2} ) выражают упругую потенциальную энергию пружины ​( E_{у1} )​ и ( E_{у2} ) в точках с координатами ​( x_1 )​ и ( x_2 ), соответственно. Таким образом, работа силы упругости равна изменению упругой потенциальной энергии пружины:

Рассмотрим простой пример. Насколько возрастет упругая потенциальная энергия пружины с коэффициентом упругости 1,0·10^-2 Н/м при сжатии ее на 10 см? Подставляя значения в формулу

получим:

Учтите, что при изменении упругой потенциальной пружины с грузом (при отсутствии внешних сил) изменяется кинетическая энергия груза. Причем эти изменения происходят так, что неизменной остается полная энергия системы, состоящей из пружины и груза. Например, при достижении точки равновесия пружина полностью разжимается, и ее упругая потенциальная энергия становится равной нулю, а кинетическая энергия груза при этом становится максимальной. И наоборот, при максимальном сжатии или растяжении пружины ее упругая потенциальная энергия становится максимальной, а кинетическая энергия груза при этом становится равной нулю.

Качаемся вместе с маятником

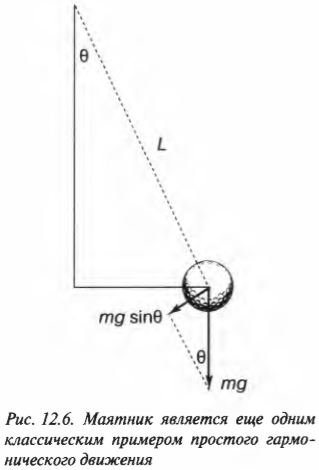
Еще одним типичным примером простого гармонического движения (кроме груза на пружине) является простой маятник, который показан на рис. 12.6.

Можно ли движение маятника описать математическими формулами простого гармонического движения, которые (выше в этой главе) использовались для описания движения груза на пружине? Да, и вот почему.

Дело в том, что на маятник, подвешенный на нити длиной ​( L )​ и отклоненный на угол ​( theta )​, действует сила гравитационного притяжения ​( mathbf{F}=mmathbf{g} )​. Перпендикулярная нити компонента силы создает сопротивление движению:

Момент этой компоненты силы

определяет угловое ускорение маятника ​( alpha )​:

Отсюда получаем формулу математического маятника:

(Математическим маятником называется идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешен груз с массой, сосредоточенной в одной точке. — Примеч. ред.)

При малых колебаниях, т.е. при малых значениях угла ​( theta )​; можно считать, что ​( sin(theta)approxtheta )​, и тогда прежняя формула приобретает следующий вид:

Эта формула связи ускорения и перемещения объекта очень похожа на прежние формулы простого гармонического движения груза на пружине и мячика по окружности (см. ранее в этой главе). Но прежде в эту формулу входило линейное перемещение, а теперь — угловое.

По аналогии с прежними формулами связи ускорения и перемещения объекта, совершающего простое гармоническое движение, коэффициент пропорциональности между ускорением и перемещением ​( g/L )​ равен квадрату циклической частоты ​( omega^2 )​. Отсюда получаем, что:

Далее, поскольку ​( omega=2pi!f )​ и ( omega=2pi/T ), то после подстановки предыдущего выражения в эти формулы получим:

и

Обратите внимание, что период качаний математического маятника не зависит от его массы!

Рисунок 2.2.1.

Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:

откуда

Частота называется собственной частотой колебательной системы.

Период гармонических колебаний груза на пружине равен

При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

или

(*)

где

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда _m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то _m = , .

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 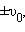то

Таким образом, амплитуда _m свободных колебаний и его начальная фаза определяются начальными условиями .

Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:

Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)

где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.

По аналогии с грузом на пружине можно получить:

Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

Колебания груза на пружине — формулы, уравнения и задачи

Теория периодичности относится к общей физике. Повторяемость некоторых процессов в течение времени определяют с помощью различных величин, например, угла, напряжённости, температуры. Для изучения явления удобно использовать маятник. Одним из его видов является пружина с грузом. Колебания в такой системе зависят от периода, частоты и амплитуды. Узнать эти параметры можно, зная начальные условия и уравнения, описывающие механическую работу.

Общие сведения

Колебания — это изменения какой-либо величины в точности или приблизительно повторяющиеся во времени. Если рассматривать процесс, с точки зрения механики, то он описывается положением тела. Повторение в точности является периодическим. Математически это можно записать формулой: x (t + T) = x (t), где T — время, в течение которого совершается одно полное колебание (период). Число циклов принято обозначать буквой N. Его находят как отношение времени к периоду: N = t / T.

При исследовании процесса не всегда бывает удобно оперировать временем, поэтому часто используют число колебаний за единицу времени. Эта величина называется частотой. Находят её количество по формуле: f = 1 / T. Доказать справедливость приведённого равенства просто. Число колебаний зависит от времени и частоты: N = f * t. Отсюда: f = N / t = (t / T) / t = 1 / T.

Очень важно не только понимать суть характеристик колебания, но и знать единицы его измерения. Вот основные из них:

• период — секунды (с);
• частота — герцы (Гц);
• число колебаний — безразмерная величина.

Если в течение времени меняется и координата, то периодически будет изменяться и скорость. Значит: vx (t + T) = Vx (t).

Исходя из верности равенства, можно сказать, что условие периодичности будет справедливо и для проекции, то есть изменения ускорения. Отсюда следует, что сила действующая на тело тоже будет переменной: Fx (t + T) = Fx (t).

При процессе также происходит изменение потенциальной и кинетической энергий. Действительно, так как в процессе колебания скорость не является постоянной величиной, то соответственно будет меняться кинетическая работа. Потенциальная же энергия зависит от координат. Например, если рассмотреть период колебаний пружинного маятника, то за это время тело переместится из нижнего положения в верхнее и вернётся обратно. Значит, координата физического объекта изменится от нуля до какого-то граничного значения.

Следует отметить, что периодичные движения обязательно будут происходить в той системе, в которой есть положение равновесия. Причём оно должно быть устойчивым. То есть существует равнодействующая сила, стремящаяся привести объект в положение, соответствующее покою. Поэтому для поддержания отклонений нужна дополнительная сила. Колебательную систему (осциллятор) под действием вынужденной периодической силы называют вынужденной.

Пружинный маятник

Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.

При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое. Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.

Можно выделить два достаточных условия возникновения свободных колебаний:

Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.

Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).

Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.

Зависимость периода

При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.

Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:

k m	m0	2m0
k0 / 2	0,68	0,93
k0	0,46	0,64
2k0	0.34	0,47

Эти данные можно проанализировать. Выводы будут следующими:

• с ростом массы физического тела период цикличности увеличивается;
• по мере увеличения жёсткости период колебаний уменьшается.

Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.

По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.

Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c 2 * м/м) = √с 2 = с.

Для написания полной формулы в равенство нужно вести ещё коэффициент. Он будет равняться 2p. Значит, период колебаний пружинного маятника количественно описывается выражением: T = 2p * √ (m / k).

Примеры решения задач

Практические задания помогают лучше разобраться в теоретическом материале и запомнить нужные для решения формулы. Существуют различные примеры, с помощью которых можно довольно быстро проработать весь изученный курс. Вот два задания с подробным описанием решения на вычисления параметров пружинных колебаний тела. Разобравшись в них, можно переходить к самостоятельному вычислению более сложных примеров.

Задание № 1. Груз, подвешенный к пружине, перемещается циклически по вертикальной оси. За восемь секунд он совершил тридцать два колебания. Определить частоту. Итак, по условию задания дано время t = 8 c и число полного перемещения тела N = 32. Чтобы решить эту задачу нужно воспользоваться формулой нахождения периода: T = t / N. Все величины для этого есть: T = 8 c / 32 = 1 / 4 = 0,25 секунды. Частота связана с периодом выражением: f = 1 / T. После подстановки чисел получится ответ равный четырём герцам.

Задание № 2. Грузик совершает колебания на пружине с жёсткостью сто ньютон на метр. При этом максимальная скорость движения составляет два метра в секунду. Вычислить массу тела учитывая, что максимальная амплитуда отклонения от точки покоя составляет десять сантиметров. Силой трения пренебречь.

При решении примера нужно рассуждать следующим образом. Когда будет максимальное растяжение пружины, то скорость груза равна нулю: V1 = 0. Значит, кинетическая энергия тоже будет нулевой: Ek1 = 0.

В этот момент останется только потенциальная энергия вытянутой пружины Ep1. В положении равновесия скорость тела максимальная и равняется V = 2 м/с. Так как пружина в этот момент нерастянута и несжатая, то Ep = 0.

По закону сохранения энергии: Ek1 + Ep1 = Ek + Ep. Кинетическая работа при растянутой пружине равняется нулю, так же как и потенциальная в состоянии покоя, значит, Ep1 = (k * L 2 ) / 2, где L — удлинение, а k — жёсткость. Энергию же можно найти так: Ek = mV 2 / 2. Так как тело совершает колебания около положения равновесия, то вытянутость пружины будет равняться амплитуде.

Перед тем как непосредственно переходить к составлению итоговой формулы и вычислениям необходимо все значения измерений привести в соответствии с СИ. Так, амплитуда указана в сантиметрах, поэтому её нужно перевести в метры. Теперь можно переходить к составлению отношения и подстановки данных: (k * L 2 ) / 2 = mV 2 / 2. Отсюда: m = (k * L) / V 2 = (100 Н/м * 0,1 2 м) / 2 2 м/с = 1 / 4 = 0,25 килограмма.

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) )  – начальная длина пружины;

( L left(text{м} right) )  – конечная длина растянутой пружины;

( Delta L left(text{м} right) )  – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу,  например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot  left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости) пружины.

Выводы

1. Упругие тела – такие, которые сопротивляются деформации;
2. Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
3. Деформация – изменение формы, или размеров тела;
4. Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
5. Удлинение пружины – это разность ее конечной и начальной длин;
6. Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
7. Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
8. Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
9. А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Формулы пружинного маятника в физике

Формулы пружинного маятника

Определение и формулы пружинного маятника

Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

[ddot{x}+{omega }^2_0x=0left(1right),]

где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

[T=2pi sqrt{frac{m}{k}}left(4right).]

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]

начальная фаза при этом:

[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

[E_p=-frac{dF}{dx}(8)]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]

Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]

где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Читать дальше: формулы равноускоренного прямолинейного движения.

Рис. (1). Колебания пружинного маятника

Рассмотрим простейший пружинный маятник — движущееся по горизонтальной плоскости твёрдое тело (груз), прикреплённое пружиной к стене (рис. (1)). Допустим, что силы трения не оказывают существенного влияния на движение груза.

Первоначально пружина не деформирована (не растянута и не сжата), поэтому никакие силы в горизонтальном направлении на груз не действуют. Точка О — положение равновесия груза.

Переместим груз вправо. Пружина при этом растянется, и в ней возникнет сила упругости, направленная влево, к положению равновесия, и по модулю равная:

где (x=A) — максимальное (амплитудное) отклонение груза от положения равновесия.

Если отпустить груз, то под действием силы упругости он начнёт ускоренно перемещаться влево, к точке (О), по мере приближения к которой скорость груза будет возрастать от нуля до некоторого максимального значения. При приближении к точке равновесия деформация пружины уменьшается, а значит, уменьшается и сила упругости. Так как груз имеет скорость при прохождении положения равновесия, то он по инерции продолжает свое движение влево. Теперь пружина начинает сжиматься (деформация сжатия), что приводит к возникновению силы упругости, направленной вправо, т.е. к положению равновесия. По мере возрастания степени деформации пружины сила растет и все больше тормозит движение груза. В конце концов, груз останавливается.

Но сила упругости, направленная к точке (О), будет продолжать действовать, поэтому груз вновь придёт в движение в обратную сторону, вправо, и на обратном пути его скорость будет возрастать от нуля до максимального значения в точке (О).

Движение груза от точки (О) к крайней правой точке снова приведёт к растяжению пружины, опять возникнет сила упругости, направленная к положению равновесия и замедляющая движение груза до полной его остановки.

Мы описали одно полное колебание.

В каждой точке траектории, кроме положения равновесия, на груз действует сила упругости пружины, которая направлена к положению равновесия.

Рис. (2). Колебания вертикального пружинного маятника

Рис. (3). Изображение смещения маятника

Пружинные маятники широко используются в качестве акселерометра в системах управления баллистических ракет, контактных взрывателях артиллерийских и авиационных боеприпасов и т. п.

Акселерометр (лат. accelero — «ускоряю» и др.-греч. μετρέω — «измеряю») — прибор, измеряющий проекцию кажущегося ускорения (разности между истинным ускорением объекта и гравитационным ускорением). Как правило, акселерометр представляет собой чувствительную массу, закреплённую в упругом подвесе. Отклонение массы от её первоначального положения при наличии кажущегося ускорения несёт информацию о величине этого ускорения.