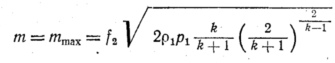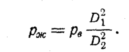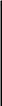Как найти скорость потока газа

Калькулятор позволяет определить скорость природного газа в трубе согласно ГОСТ Р 55472-2019 «Системы газораспределительные. Сети газораспределения природного газа. Часть 0. Общие положения».

Общие данные.

При расчете пропускной способности надземных газопроводов учитывают максимально допустимый уровень шума, создаваемого движением газа, по ГОСТ 12.1.003-2014 «Система стандартов безопасности труда. Шум. Общие требования безопасности».

Скорость движения газа рассчитывается по формуле п.7.1.6. ГОСТ Р 55472-2019 «Системы газораспределительные. Сети газораспределения природного газа. Часть 0. Общие положения». Формула учитывает коэффициент сжимаемости газа, температуру и давление газа. Формула составлена на базе уравнения идеального газа.

Коэффициент сжимаемости в случае необходимости определяется в соответствии с:

• ГОСТ 30319.2-2015 «Газ природный. Методы расчета физических свойств. Вычисление физических свойств на основе данных о плотности при стандартных условиях и содержании азота и диоксида углерода»;
• ГОСТ 30319.3-2015 «Газ природный. Методы расчета физических свойств. Вычисление физических свойств на основе данных о компонентном составе».

При этом следует учесть, что для газопроводов с давление газа до 1,2 МПа коэффициент сжимаемости лежит в пределах от 0,98÷1,0, поэтому в методике гидравлического расчета он не учитывается. В данном расчете по умолчанию принят коэффициент равный Z=1. Калькулятор позволяется менять значение коэффициента.

ГОСТ Р 55472-2019 предусматривает расчет абсолютного давления газа по формуле: P_a=P_и+0.1012.  Калькулятор рассчитывает абсолютное давление газа по классической формуле: P_a=P_и+0.101325.

Действующими НТД (ГОСТ Р 55472-2019, СП 42-101-2003) скорость движения газа рекомендуется принимать для газопроводов:

• • низкого давления — не более 7 м/с;
  • среднего давления — не более 15 м/с;
  • высокого давления — не более 25 м/с.

Заданные скорости газа в трубе не являются основным критериям для выбора диаметра газопровода. Диаметры газопроводов определяются в ходе полного гидравлического расчета систем газораспределения и газопотребления.

Примечание.

В комментарии приветствуются пожелания, замечания и рекомендации по улучшению программы.

Поделиться ссылкой:

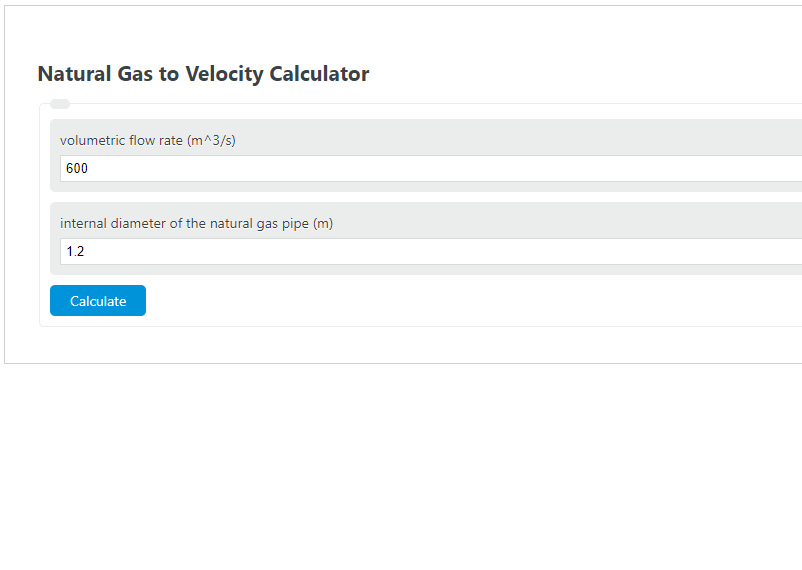
Проводимость канала определяет его способность транспортировать газ. Она выражается в единицах объема газа, проходящего через данное сечение в единицу времени. Зависимости для расчета проводимости элемента, работающего в различных условиях, являются весьма сложными и зависят от режима течения, а также от геометрических параметров канала и свойств его поверхности. Расчеты проводимости и потока газа при турбулентном режиме течения трудно трактовать аналитически. Количественное определение параметров вязкостного потока также представляет трудности, поскольку зависит не только от формы канала, но и от давления газа. Однако при тех диапазонах давлений, которые имеют место в условиях высокого вакуума, поток является молекулярным, а не вязкостным.

Уравнения для расчета параметров вязкостного потока

В общем случае уравнения для расчета проводимости и потока газа при вязкостном режиме течения получены для трубопроводов и каналов, имеющих сечение простой геометрической формы — круглое или прямоугольное. Эти выражения используются, например, для расчета времени, необходимого для откачки сосуда через трубопровод, имеющий круглое или прямоугольное поперечное сечение.

Течение в трубопроводах круглого сечения

Поток газа по прямому трубопроводу круглого сечения в условиях вязкостного режима определяется уравнением Пуазейля:

$$frac{Q}{P_{1}-P_{2}}=K frac{d^{4}P}{eta L}, (60)$$

где d — диаметр трубы; L — длина трубопровода; η — динамическая вязкость газа; р — среднее давление в трубопроводе; р₁ и р₂ — давления на противоположных концах трубы.
Для сухого воздуха при 20 °С данное уравнение приобретает вид:

$$Q= frac{750d^{4}bar{P}}{L}(P_{1}-P_{2}), (61)$$

где Q — поток газа, Торр — л/с; d — диаметр трубопровода, см; L — длина трубопровода, см; р — это давление, Торр.

Проводимость круглого трубопровода, л/с, для воздуха при 20 °С приведено ниже:

$$C= frac{2,94pd^{4}}{L}, (62)$$

Течение в прямоугольных каналах

Уравнение Пуазейля для потока воздуха при 20 °С, текущего по прямоугольному каналу с большей стороной сечения а и меньшей b, имеет следующий вид, л/с:

$$C= frac{30a2b2KP}{L}, (63)$$

где К — это коэффициент формы, значение которого зависит от b/а.

Как можно видеть, проводимость прямоугольной диафрагмы (отверстия) быстро увеличивается при переходе сечения от прямоугольной щели к квадрату.
Так же, как и в случае круглого трубопровода, выражение для С позволяет получить соотношение для объемного потока газа в зависимости от перепада давлений в канале.

$$C= frac{pK}{Delta p}, (64)$$

где

$$F= frac{Cp}{Delta p}, (64)$$

Таким образом,

$$K= frac{30a_{2}b_{2}K}{L} cdot Delta p, (65)$$

л/с.

Уравнения для расчета параметров молекулярного потока

При низких значениях давления межмолекулярные столкновения происходят реже, чем столкновения со стенкой, поэтому последние определяют параметры газового потока по каналу. Проводимость канала в условиях молекулярного потока зависит от двух факторов:

1. Скорости, с которой молекулы поступают в канал.
2. Вероятности прохождения молекул по системе.

Первый фактор зависит от площади сечения входа в систему, а последний определяется последующей серией столкновений со стенками, в результате которых молекула в конечном итоге перемещается по каналу или отбрасывается обратно в откачиваемый сосуд.
Рассмотрим вначале случай очень тонкой диафрагмы в пластине. В данном случае для определения проводимости диафрагмы нас интересует ее площадь А, а не свойства стенок канала. Объем газа, проходящего через диафрагму — ее проводимость — составляет:

$$C_{a}= frac{1}{4}AV=(frac{2}{p})^{-1} — V^{0}A, (66)$$

если молекулы имеют распределение скоростей по Максвеллу. Значения проводимости зависят от молекулярной массы и кинетической энергии. Случай, когда столкновения молекул со стенками трубопровода являются более важными, чем проводимость отверстия, рассмотрен ниже.

Формула Кнутсена

Проводимость С_Υотрезка длинной трубы длиной L с переменной площадью сечения А и периметром Н была рассчитана Кнудсеном и составляет:

$$C_{Upsilon} = frac{4}{3}  sqrt{ frac{H( delta)}{A^{2} L} cdot de }. (67)$$

Были приняты следующие допущения:

1. Длина трубопровода значительно больше диаметра.
2. Направление движения отскочивших молекул после столкновения со стенками не зависит от направления их движения до столкновения.
3. Угловое распределение отскочивших молекул подчиняется закону косинуса.

Допущение 1 предполагает, что влияние отверстия является незначительным, а величина проводимости, получаемая из уравнения (67), относится к молекулам внутри трубы, удаленным от отверстия. Для получения приближенных выражений для проводимости всей трубы нужно включить последовательную проводимость отверстий. Карлсон приводит формулу для трубопровода с периметром Н, площадью Л и длиной L:

$$C_{a}=1+ frac{3}{16} cdot 9 frac{LH}{A}). (58)$$

Коэффициент Клаузинга

Проводимость длинного трубопровода связана с проводимостью входного отверстия коэффициентом [1 +3/16(LH/A)]^-1 C_a. Этот коэффициент можно интерпретировать как вероятность случайного входа молекулы в отверстие и ее прохождения до самого конца трубопровода.

Целесообразно рассматривать проводимость с точки зрения проводимости отверстия и соответствующей вероятности прохождения молекулы (коэффициента Клаузинга), поэтому

$$C=CA cdot P_{1 to 2}= 1/4vA_{1}P_{1to 2}. (69)$$

Так как проводимость не зависит от направления движения молекул,

$$A_{1}P_{1 to 2} = A_{2} P_{1 to 2}. (70)$$

Примеры. Выражение для потока газа по длинному прямому трубопроводу было дано Кнудсеном:

$$Q= frac{ pi d^{3/2}}{L}$$

$$Q=( pi d^{3/2}/L)n_{a}(P_{1}-P_{2}), (71)$$

где d — диаметр трубопровода; L — длина трубопровода; n_а — средняя скорость молекулы; р₁ и р₂ — давления на противоположных концах трубопровода.
Для сухого воздуха при 20 °С d и L, выраженных в дюймах, а р — в Торр, данное уравнение принимает следующий вид:

$$Q=(80d^{3}/L)n_{a}(p_{1}-p_{2}), (72)$$

Приблизительные значения некоторых вероятностей прохождения имеют точность в пределах + 10%. Это разнообразные методы, которые включают аналитические методы, расчеты по методу пробной частицы Монте-Карло и методу вариаций. Карлсон исследовал различные геометрические формы и ссылается на соответствующие источники. Примеры числовых расчетов можно найти в работе Карлсона.

Течение газа

Инженерные
расчеты течения газа в элементах
пневмосистем сводятся к
расчетам, связанным с истечением газа
из резервуаров (баллонов) и с запол­нением
их, а также с течением по трубопроводам
пневмосистем и через мест­ные
сопротивления.

Эти
расчеты в силу сжимаемости воздуха
представляют известные труд­ности,
обусловленные тем, что течение его в
трубопроводах пневмосистем и
каналах их агрегатов сопровождается,
как это было указано, изменением давления
и удельного объема. Ввиду этого при
расчетах исходят из условия, что
при установившемся процессе течения
массовый расход воздуха т
через
любое
поперечное сечение трубопровода площадью
/, остается постоянным, в
соответствии с чем массовый расход
определяется из уравнения сплош­ности
(неразрывности) потока

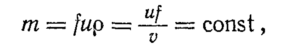
по
пути течения воздуха по трубопроводу
не сохраняется, а увеличивается вследствие
расширения, вызванного понижением
давления при течении согласно
выражению (71), средняя скорость воздуха
по длине трубопро­вода и
=
Q/f
также будет возрастать. При этом
вследствие расширения воздуха
происходит также изменение его
температуры, что и должно быть учтено
при расчетах.

В
основу расчетов течения газа в элементах
пневмосистем положено известное
из курса «Гидрогазодинамика» уравнение
движения идеального газа
в адиабатном режиме

Истечение
газа из резервуара неограниченной
емкости. Расчеты
исте­чения
газов (воздуха) из резервуаров
неограниченной и ограниченной ем-

кости
и наполнения последних являются основными
в расчетах пневмо­систем.
Истечение газа в общем случае имеет
место при разрядке гидроакку­муляторов,
при опорожнении пневмоцилиндров и пр.

Принимая
в уравнении (75) и_х
=
0 (т. е. пренебрегая скоростью газа в
расходном резервуаре), находим расчетную
скорость истечения газа u₂
= и
из
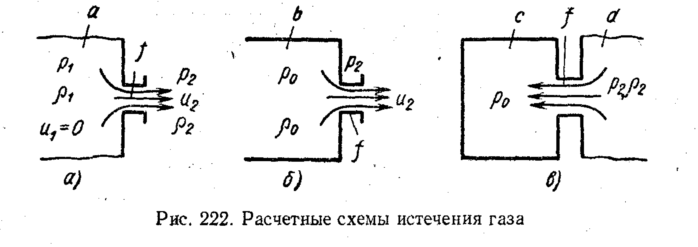
резервуара а
неограниченной
(бесконечной большой) емкости (рис. 222,
а) через,
круглое отверстие (или насадок) в стенке
при адиабатном процессе:

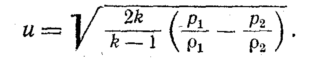
Для течения
идеального газа имеем

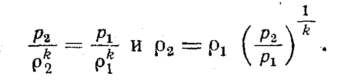
Подставив эти
значения в уравнение (76) и преобразовав,
получим

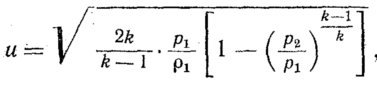
Массовый
расход т
газа,
протекающего со скоростью и
через
отверстие площадью
f,
кг/сек:

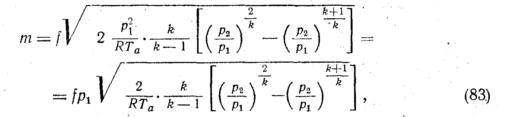
где
T_a
—
температура газа на входе в дросселирующее
отверстие в К.

Приведенные
расчеты произведены без учета потерь,
обусловленных трением,
теплообменом и прочими факторами. Учет
этих потерь обычно производят,
принимая, что процесс протекает по
политропному режиму. В
этом случае расход газа рассчитывают
по выражению (81) с заменой пока­зателя
адиабаты k
на
показатель политропы п,
значение
которого прини­мают равным п
— 1,3
— 1,35.

Потери
на трение учитывают часто коэффициентом
расхода х
вводя
его
в приведенную формулу (81) для адиабатного
процесса.

В
результате получают формулу для массового
расхода с учетом трения

Критическое
расширение газа. Максимальный массовый
расчетный расход
газа соответствует условию равенства
_ж
нулю производной в урав­нении
(80).

Максимальный
расчетный расход соответствует
критическому расши­рению
газа (критическому отношению давлений)

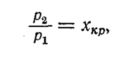
при
котором скорость истечения по уравнению
(78) становится равной ско­рости звука
в газе при параметрах последнего,
соответствующих параметрам на выходе
из дросселирующего сопла [см. уравнение
(77)].

Параметры
критического расширения, при котором
имеет место наиболь­ший расход, получим
путем исследования функции

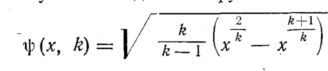
на максимум, в
результате чего будем иметь

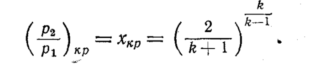
Для
адиабатного процесса х_кр
=
0,528. Это условие соответствует скорости
течения, равной местной скорости
распространения звука.

Приведенные
теоретические расчеты истечения через
отверстие при допу­щении
адиабатного режима могут быть с
достаточной точностью применены и
для практических расчетов истечения
через короткий насадок, при котором
можно
пренебречь силами трения, а также
вследствие кратковременного нахождения
газа в насадке пренебречь и теплообменом
с окружающей средой.

Анализ функции

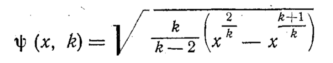
показывает
[см. также равенство (85)], что имеются две
зоны (области) тече­ния:

зона,
соответствующая рассмотренному выше
условию х_кр
<^х <С
1, ко­торая
носит название зоны докритического
(подкритического) течения (ско­рость
газа в этой зоне ниже скорости звука);

зона,
соответствующая условию 0<^x<^x_KF,
которая
носит название зоны
надкритического течения (скорость газа
в этой зоне постоянна и близка или
равна скорости звука).

В
соответствии с этим различают процессы,
протекающие в подкрити-ческом
(ниже критического) и надкритическом
режиме.

В
надкритической зоне имеет место
максимальный и постоянный мас­совый
расход, соответствующий критическому
расширению газа. Формулу для
определения расхода в этой зоне получим,
подставив в уравнение (80) значение
критического расширения газа

С учетом потерь
на трение

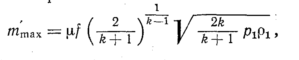
где μ
—
коэффициент расхода (см. выше).

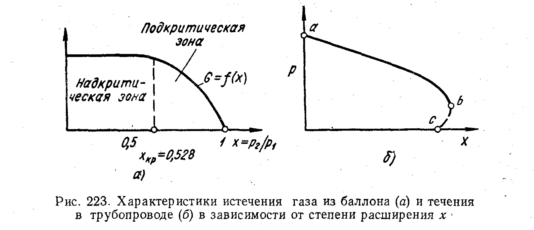
График
изменения расхода т,
отложенного
по оси ординат, в функции

показан
на рис. 223, а.
В
надкритической зоне (x
<
0,528) имеем постоян­ный и максимальный
массовый расход, в подкритической —
переменный расход,
уменьшающийся с увеличением х.

Пользуясь
приведенными уравнениями, покажем, что
расход газа при истечении
его со скоростью распространения звука
в газе (соответствует и_кр)
является
максимальным.

Очевидно,
максимальному расходу, выражаемому
уравнением (86), соот­ветствует
максимальная (критическая) скорость
истечения газа согласно уравнению (78):

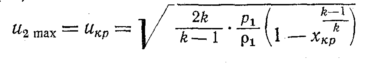
или с учетом
уравнения (85)

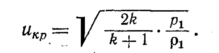
Преобразуя уравнения
(85) и (77), получим

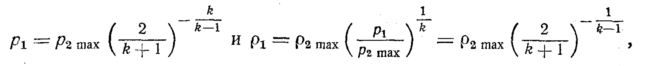
а затем критическую
скорость истечения

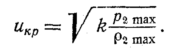
Из
сравнения уравнений (88) и (74а) следует,
что максимальная (крити­ческая)
скорость газа (а следовательно, и
максимальный его массовый рас­ход)
имеет место при скорости звука в газе

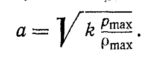
Опорожнение
резервуаров ограниченной емкости. В
инженерной практике в
основном приходится производить расчеты,
связанные с опорожнением и наполнением
резервуаров (баллонов) ограниченной
емкости. К этим случаям
относятся опорожнение газовых баллонов
в процессе питания пнев-мосистем,
наполнение или опорожнение пневмоцилиндров
и пр.

Истечение
газа из резервуара ограниченной емкости
характеризуется тем,
что при ограниченной емкости резервуара
параметры истекающего газа будут
переменными по времени.

Рассмотрим
процесс опорожнения баллона b
объемом
V_o
через
отверстие площадью / (рис. 222, б).
Дифференциальное
уравнение истечения газа из такого
баллона составляют исходя из условия,
что масса т
газа,
проте­кающего
через заданное поперечное сечение
отверстия за некоторый отрезок времени,
равна изменению массы dm
=
V_o
dp,-
(где V₀
— объем баллона, Pi
— текущее значение плотности газа) газа
в баллоне за то же время.

Пусть
в некоторый отрезок времени с момента
открытия отверстия (насадка)
опоражниваемого баллона абсолютное
давление в баллоне было равно
Pi
и
плотность газа в нем р_£.
Элементарная масса dm
газа,
прошедшая через это отверстие площадью/
за отрезок времени dt,
равна
согласно урав­нению (80)

где
pi
и
ρi
—
текущие значения давления и плотности
газа в баллоне.

Выражая текущие
параметры газа p_t
и р^ через
начальные их значения р₀
и р₀,
имевшие место в баллоне перед началом
истечения, и полагая, что изме­нение
этих параметров внутри баллона при его
опорожнении (истечении газа)подчиняется
некоторой политропной зависимости с
показателем политропы n,
получим

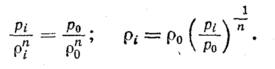
Подставив уравнение
(90) в уравнение (89), получим

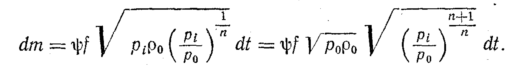
Составим
теперь выражение для изменения массы
газа в баллоне за тот же
отрезок времени dt.
Эта
масса в момент времени t
равна
т
=
V₀
ρi
,
а следовательно,

где
V_o
— объем
баллона.

С учетом уравнения
(90) получим

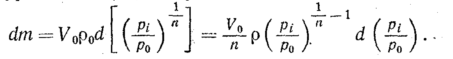
Приравняв
уравнения (91) и (92), получим (с учетом
знака) дифферен­циальное
уравнение опорожнения рассматриваемого
баллона ограниченной емкости
V_o

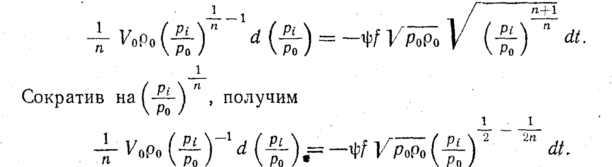
Для
интегрирования этого уравнения (при /
= const)
произведем пре­образование:

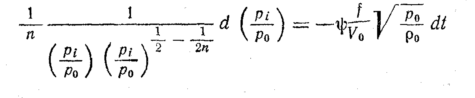
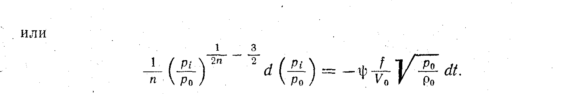
После преобразований
получим

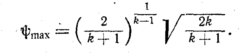
Подставив
ψ_max
в дифференциальное уравнение (93), получим

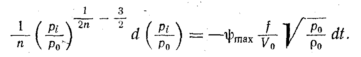
Интегрируя
в пределах от р₀
до
p_t
и
от t
==
0 до t,
имеем

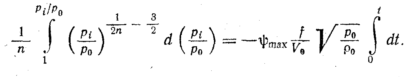
Преобразуя,
получим уравнение для вычисления времени
t
частичного
опорожнения
баллона для заданного условия понижения
давления в бал­лоне
с начального р₀
до
заданного р_л
для
режима, соответствующего надкри­тической
области, когда p₀>Pi>Р₂/х_кр:

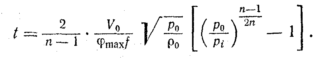
Полное
время истечения в надкритической
области, соответствующее понижению
давления от р₀
до
Р₂/х_кр
вычисляется путем подстановки в
урав­нение (94)

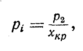
в результате чего
после преобразований получим

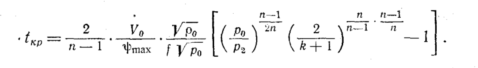
Аналогичным
путем можем получить дифференциальное
уравнение исте­чения в подкритической
области для понижения давления до p_i

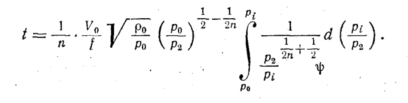
Ввиду
сложности функции это уравнение обычно
решается графо-аналитическим
путем и здесь не рассматривается.

Наполнение
резервуара ограниченной емкости. К
случаям наполнения резервуаров
ограниченной емкости относятся наполнение
пневмоцилиндров пневмосистем,
зарядка газогидравлических аккумуляторов
и пр. При запол­нении
сжатым воздухом какой-либо емкости
воздух в начальный момент, когда
давление в заполняемой емкости
минимальное, течет, расширяясь с
максимальной скоростью, которая, по
мере выравнивания давления в питаю­щей
магистрали и заполняемой емкости
понижается, достигая при полном
выравнивании этих давлений нулевого
значения. Очевидно, при этом будет
переменной вследствие расширения
воздуха и его температура, причем
изме­нения
ее
могут
происходить в широком диапазоне.

Пусть
к емкости d
с
неограниченным объемом и постоянным
давлением р₂
подключается
емкость (баллон) с
с
объемом V_o
и
давлением р₀
<Ср₂
(рис.
223). При этом допускаем, что объем источника
расхода d
настолько
велик,
что, изменением давления и изменением
скорости перемещения частиц газа
в нем при заполнении емкости с
можно
пренебречь.

Определим
время повышения давления в подключаемом
баллоне с р₀
до
Pi
⁼
Р₂
т.
е. определим время выравнивания давления
между источником расхода
и заполняемым баллоном.

Пусть
в момент времени t
давление
в баллоне будет p_t,
плотность
газа в струе р и скорость и.
Масса
dm
газа,
втекающая в баллон через отверстие
постоянного сечения f
за время dt,
составит

где и
—
скорость газа, определяемая по уравнению
(78).

Решая
дифференциальное уравнение (95) с учетом
скорости и
и
функций

получим
уравнение для элементарной массы dm
газа,
протекающей через поперечное сечение
/ струи за элементарный отрезок времени
dt:

где
Т₂
— абсолютная температура газа, вычисленная
по характеристиче­скому уравнению
(73).

Составим
теперь уравнения для изменения массы
газа в резервуаре за тот
же промежуток времени dt

:

Исследования
показывают, что процесс наполнения
резервуаров (балло­нов)
изменяется от адиабатного в начале
наполнения до изотермного в конце
наполнения,
в результате температура в резервуаре
постепенно стремится от
T_t
к
Т₂.
Полагая Т_i
≈T₂,
получим

При этом

С учетом последнего
равенства уравнение (97) примет вид

Приравняв правые
части уравнений (96) и (98), получим

откуда

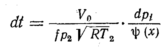
Принимая во
внимание, что

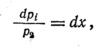
получим

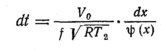
Интегрируя это
уравнение в пределах

получим
с учетом характера протекающего процесса
(над- или подкритический)
искомое время наполнения:

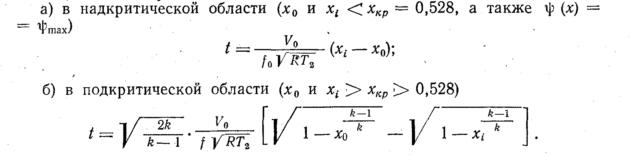
Фактически
истечение будет происходить не по
адиабатному, а по поли-тропному
циклу, ввиду чего для расчетов необходимо
зиать показатель поли­тропы.
Опыт показывает, что если опорожнение
(или наполнение) емкости происходит
через отверстие (дроссель) или короткий
патрубок, при котором заметного
теплообмена с внешней средой не
происходит, показатель поли­тропы
будет близок к показателю адиабаты п
≈ & k
и

С
уменьшением показателя поли­тропы п
значение
Р₂/Р₁
возрастает, дости­гая при п
= 1

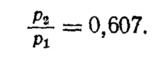
Течение
газа в трубопроводе. Важным
для практики является также

расчет течения
воздуха (газов) в трубопроводе.

Для
вывода дифференциального уравнения
установившегося течения

газа
в трубопроводе выделим элементарный
отрезок его длиной dx
(рис.
224, а) и, применив к эле­ментарному
объему газа dV
= ~fdx,
показанному
точечной штриховкой,
уравнение коли­чества
движения (неравномер­ностью
распределения скоро­стей
по сечению трубопровода пренебрегаем),
напишем

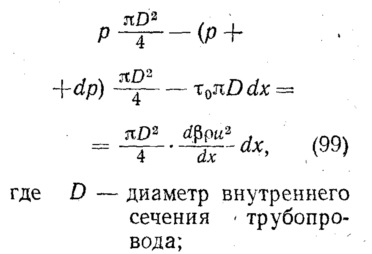
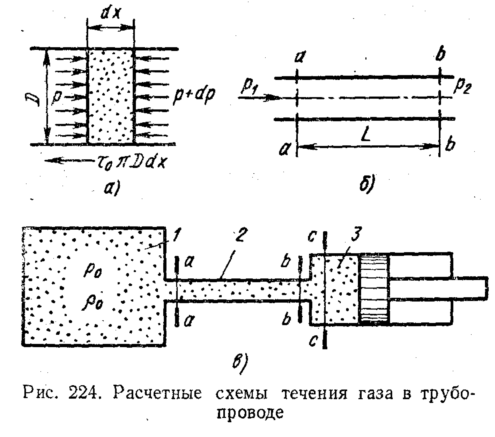
Преобразуем правую
часть уравнения

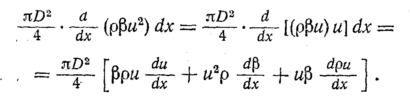
С учетом неразрывности

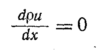
уравнение (99)
принимает вид

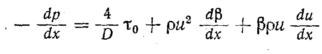
Для
турбулентного режима течения, при
котором средняя скорость потока и
давление в каждом его сечении сохраняются
практически постоянными (соответствует
установившемуся режиму течения), можно
принять β = 1 и соответственно

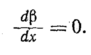
В результате
получим

Подставив касательное
напряжение сдвига слоев жидкости

получим
дифференциальное уравнение течения
газа в трубопроводе

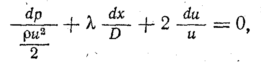
где λ
— коэффициент сопротивления трения
[этот коэффициент можно рас­считать
по выражению (17) при условии подстановки
средних значений входящих
в него параметров].

Проинтегрировав’
приведенное дифференциальное уравнение
с учетом заданного
газового процесса, получим уравнение
установившегося течения газа
в трубопроводе с учетом трения.

Расчеты
и опыт показывают, что вследствие
теплообмена течение газа может
быть близким к адиабатному лишь при
очень коротких отрезках тру­бопроводов
(в местных сопротивлениях) и при больших
перепадах давления (расширениях
газа). При длинных же трубопроводах этот
процесс в обычных условиях
более близок к изотермному, а при
известной длине трубопроводов является
изотермным, т. е. температура газа в этом
случае сохраняется практически
постоянной по всей длине трубопровода.
В соответствии с этим при
длинных трубопроводах, и в особенности
при малых перепадах давления, справедлива
изотермная зависимость

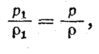
Кроме того, из
условия неразрывности потока

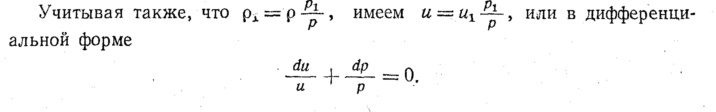
В соответствии с
этим первый член уравнения (101) примет
вид

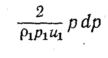
Кроме того, так
как

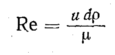
в
рассматриваемом процессе практически
не изменяется по длине трубо­провода
(uр
= const,
μ = const,
относительная шероховатость трубы k/d
= const),
то постоянным по длине трубопровода
будет также и коэффициент трения λ,

С
учетом этого интегрирование
дифференциального уравнения (101) по
ллине L
отрезка
трубопровода даст (рис. 224, б)

Так
как логарифмический член в скобках,
последнего уравнения мал по
сравнению с Х-^-,
то
этим членом обычно пренебрегают. В
результате получим
упрощенное выражение

Из
этого уравнения следует, что при течении
газов падение давления по длине
трубопровода выражается степенной
зависимостью, а не линейной, как
это имеет место при течении жидкостей,
что видно из уравнения (16).

Введя
в уравнение (102) число Маха

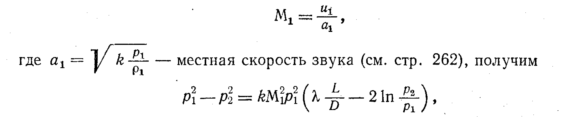
Уравнение
(103) позволяет рассчитать давление в
трубопроводе на тре­буемом расстоянии
L
от
начального (исходного) сечения, для
которого задано число
Маха.

Решая
уравнение (103) относительно λ*L/D,
получим

Последнее
уравнение показывает изменение
безразмерной длины LID
трубопровода
в функции отношения давлений газа Р₂/Р₁

Пренебрегая
логарифмическим членом, уравнение (104)
можно пред­ставить
в виде

С
учетом числа Маха дифференциальному
уравнению (101) можем при­дать
иную форму, подставив

При этом получим

Общий
характер изменения давления р
по
длине трубопровода показан на
рис. 223, б.
Течение
газа может существовать лишь на участке
кри­вой а—b.
Отрезок
кривой b—с
соответствует
сверхзвуковому течению. Точка
Ъ
называется
предельной точкой. Число Маха для
состояния потока газа
в этой точке называется предельным
числом Маха М_пр.
Соответственно этому
существуют предельное (низкое) давление
р_пр
и
предельная наиболь­шая
длина L_np.

Поскольку
в предельной точке (сечении трубопровода)
b

знаменатель
уравнения (105) будет равен нулю, и
предельное число Маха

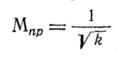
Следовательно,
скорость воздуха в трубопроводе может
возрастать лишь до
тех пор, пока число Маха не достигнет в
предельном сечении, которое должно
находиться в конце трубопровода, значения

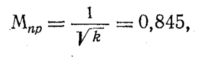
Для
нахождения минимального предельного
давления в трубопроводе, соответствующего
этому условию, воспользуемся равенством.

с учетом которого
получим

откуда

Подставив
из последнего равенства р_пр
в
уравнение (104), получим

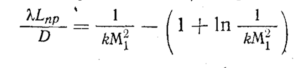
или

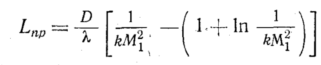
С учетом равенства

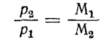
можем получить

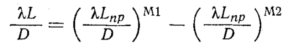
Из
приведенного анализа следует, что
скорость течения газа (и число

Маха)
возрастает до наибольшей (предельной)
величины (M_np
=
1/√k
) в
некоторой предельной точке, которая
должна быть в конце трубопровода.
Максимальный
расход газа при течении в режиме

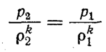
имеет
место при М = 1. При М > 1 давление в потоке
по длине трубопро­вода
и скорость потока не зависят от давления
в конце трубопровода. В этом случае
силы трения затормаживают поток (скачок
уплотнения), ввиду чего течение
со сверхзвуковой скоростью возможно
лишь в пределах определен­ной
(критической) длины трубопровода. Если
длина трубопровода превышает
это значение, то в некотором его сечении
возникает скачок уплот­нения,
в результате которого сверхзвуковая
скорость скачкообразно перей­дет в
дозвуковую. После этого скачка уплотнения
характер течения газа изменится:
скорость вдоль трубопровода вновь
увеличивается, а давление и
плотность газа уменьшаются.

Предельное
отношение давлений (расширение газа)
Р₂/Р₁
и
предельная длина L_np
зависят
лишь от показателя адиабаты k
(от
начального числа Маха). Соответственно
минимальное предельное давление р_пр
в
трубопроводе и предельную
(наибольшую) длину трубопровода L_np
можно
выразить так:

П
рактически
в трубопроводах реальных длин критическая
степень рас­ширения
х_кр
не
достигается, т. е. течение газа по
трубопроводам длиной больше
L_np
происходит
в зоне докритического режима течения.

Наполнение
пневмоцилиндра газом через длинный
трубопровод. Рассмо­трим
схему подвода воздуха к пневмоемкости,
показанную на рис. 224, в.
Воздух
из воздухосборника (ресивера) / направляется
по трубопроводу 2
в
пневмоцилиндр 3.

При
течении газа по этой схеме можно выделить
три участка: 1) истечение из воздухосборника
в трубопровода 2) течение по трубопроводу;
3) истечение из
трубопровода в цилиндр. Соответственно
этому должны быть составлены уравнения,
дающие систему, подлежащую решению.
Задача получается сложной,
ввиду чего рассмотрим приближенное
решение со следующими допу­щениями:
давление р_а
при
входе в трубопровод (сечение а—а)
равно
давле­нию
р₀
в воздухосборнике и течение в трубопроводе
изотермное.

Обозначив
через т
массовый
расход воздуха, получим:

1)
скорость газа в сечении а—а
согласно
уравнению (79)

2)
массовый расход, вычисляемый по параметрам
сечений b—b
и
с—с
согласно
уравнению (79):

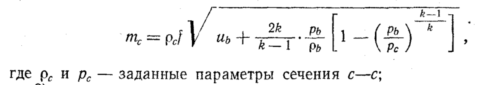
3) связь
между давлениями р_а
и
р_ь
согласно
уравнению (101)

Последнее
уравнение вместе с уравнением (107)
представляет систему уравнений
с двумя неизвестными р_ь
и
т,
к
решению которой и сводится наша задача.

Приближенные
расчеты течения газа в трубопроводах.
Выше
было ука­зано,
что при достаточно длинных трубопроводах
показатель политропы в
силу сопротивлений при течении газа
близок (даже в случае полной тепло­вой
изоляции) к единице.

Если
принять, что температура будет сохраняться
постоянной, то посто­янной
будет также и вязкость. воздуха, а
следовательно, и Re,
значение которого
необходимо для вычисления коэффициента
сопротивления трения к
по
выражению (17).

С
учетом указанного для приближенных
расчетов потерь напора по длине
трубопровода
может быть применена известная формула
гидравлики (1,4) с подстановкой средних
значений входящих в нее параметров. При
пользо­вании
этой формулой газ условно представляется
в виде несжимаемой жид­кости,
имеющей некоторые средние параметры:

Расчеты
показывают, что течение воздуха в
каналах пневмосистемы носит
обычно турбулентный характер (Re
> 2300), в соответствии с чем коэффициент
к
вычисляют
по тому же выражению, что и при расчетах
кана­лов
гидросистем.

В
практике при 2300 < Re
< 10⁸
часто применяют также эмпирическую
формулу,
учитывающую шероховатость поверхности
трубопровода:

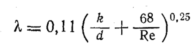
Величина
Re,
входящая в эту формулу, рассчитывается
в данном случае по уравнению (11), которое
при подстановке массового расхода

и средних значении
входящих параметров примет вид

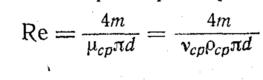
Приняв приближенно

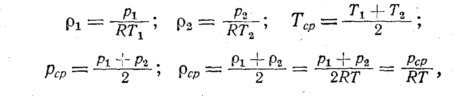
уравнение (108) можно
представить в виде

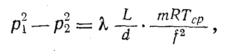
где R
—
газовая постоянная при средних значениях
давления р_ср
и
темпе­ратуры

Течение
газа через местные сопро­тивления.
Местные
сопротивления в си­стеме
пневмопривода, как и в системе гидропривода,
играют важную роль, так

как
от правильности оценки параметров
потока воздуха, протекающего через
местные сопротивления, зависят точность
и надежность расчетов пневмосистем.

В
отличие от течения жидкости, при котором
энергия потока, расходуемая на преодоление
сопротивлений, превращается в тепловую
энергию без после­дующего
обратного превращения ее в механическую
энергию, механическая энергия при
течении потока воздуха, преобразовываясь
в тепловую, частично или
полностью поглощается самим потоком
(происходит перераспределение энергии).
Ввиду этого механическая энергия потока
воздуха, израсходован­ная
на преодоление сопротивлений, не является
безвозвратно потерянной энергией,
иначе говоря, полная энергия потока
сохраняется неизменной, если
пренебречь теплообменом между потоком
и окружающей средой.

Расчет
местных сопротивлений пневмосистемы
производится в общем случае
по уравнению (84). Однако ввиду сложности
этого уравнения часто пользуются
при вычислении расхода газа через
местное сопротивление при­ближенным
равенством (109).

Для
определения потерь напора в местных
сопротивлениях пользуются в
общем случае известным из гидравлики
выражением (19).

Пользуясь
законом неразрывности потока и полагая
процесс дросселирования в местных
сопротивлениях политропным, получим в
результате преобразований
формулу для массового расхода воздуха

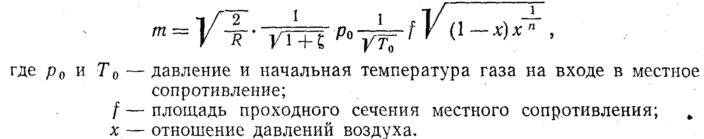
Показатель
политропы можно определить, считая
расширение политропным:

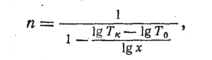
где
Т_к
—
конечная температура газа при расширении
(определяется по Т—S-диаграмме
для данного газа).

Дроссели.
Наиболее распространенным местным
сопротивлением яв­ляется
дроссель, с помощью которого изменяется
сопротивление проходу рабочей
среды (воздуха) и регулируется расход
этой среды. С помощью дросселя
также создаются элементы пневмоавтоматики,
в которых произ­водится
суммирование давлений, а также
пропорциональное изменение одного
давления в зависимости от другого и пр.

Конструктивно
дроссели пневмосистем подобны дросселям
гидросистем. В
частности, распространены дроссели в
виде отверстия в шайбе (см.
рис. 107, а).
Массовый
расход воздуха через подобный дроссель
является при М <; 1 функцией отношения
давлений газа pjpi
в
дросселирующем элементе
(здесь М число Маха):

где
р_г
и
р₂
— давления перед дросселирующим
элементом» и после него

(на выходе из
дросселя).

Принимая,
что процесс течения газа через такой
дроссель сечением f
(см.
рис. 77, а) адиабатный, фактический массовый
расход m
газа
можно вычислить:

Значение
μ
может
быть вычислено по формулам для несжимаемой
жид­кости (см. стр. 32). Практически
режим течения газа через дроссели
квад­ратичного типа (см. рис. 77) является
турбулентным. Так, принимая Re_Kp
= 2300, можно показать, что для шайбовых
дросселей турбулентный режим при
возможных перепадах давления будет
наблюдаться при d
>
0,2 мм.

Вследствие
некоторой сложности расчетов по уравнению
(80) пользуются приближенной
зависимостью, полученной исходя из
того, что функция

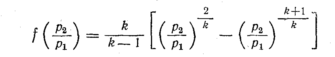
достаточно точно
аппроксимируется функцией

В соответствии с
этим массовый расход газа через дроссель

Критическое
отношение давлений газа, при котором
имеет место макси­мальный
его расход,

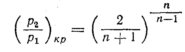
Для
адиабатного процесса значение этого
расширения равно, как это было
указано

Пользуются
также расчетной формулой, полученной
путем преобразо­вания
формулы (83) с учетом изотермного процесса:

Описываемая
последним выражением функция расширения
газа имеет значе­ние
Р₂/Р₁
= 0,5, что достаточно близко к значению
Р₂/Р₁
= 0,528, соответствующему формуле.

Применяются
также дроссели, в которых расход
регулируется изменением длины
дроссельного канала. Наиболее
распространенной конструкцией такого
дросселя является винтовой дроссель
(см. рис. 76, а).

Ар,

Подобные
дроссели обладают важным для практики
положительным качеством
— стабильностью регулирования,
заключающейся в том, что при повторных
установках дросселя в одно и то же
положение расходная харак­теристика
его сохраняется практически неиз­менной.
В дросселях этого типа может иметь место
при небольших перепадах давления
ламинарный
режим течения, характеристика которого
определяется уравнением Пуазейля

где р
— плотность воздуха, которую обычно
принимают постоянной; μ — динамическая
вязкость воздуха.

Последовательное
соединение дросселей. Путем
последовательного и

параллельного
соединения дросселей создаются элементы
пневмоавтоматики.

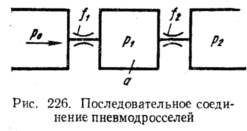
На
рис. 226 представлена схема одного из
таких элементов, получившего

название
пневмокамеры, которая представляет
собой проточную камеру,

образованную
двумя последовательно расположенными
дросселями площадью
f₁
и
f₂—
Эта камера обладает свойством
пропорционального редуциро­вания
давлений, благодаря чему она входит как
основной элемент в схемы многих
приборов пневмоавтоматики.

Допустим,
что во входном дросселе площадью /_х
имеет место подкрити-ческий
процесс течения. В этом случае расход
через этот дроссель опреде­лится
по уравнению

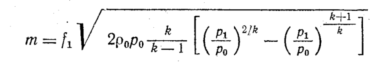
где
р₀
и ρ₀
— заданное давление и плотность газа
перед дросселем пло­щадью f_t;

p₁
—
давление в проточной камере а.

Предположим
далее, что в выходном дросселе площадью
f₂
имеет место надкритический процесс
истечения. Расход через дроссель f₂
в этом случае определится по уравнению

где
р₁
—
плотность газа в камере а.

Приравнивая
расходы и возводя обе части равенства
в квадрат, а также учитывая,
что

Получим

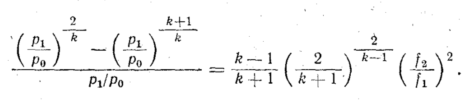
Следовательно,
при подкритическом процессе в дросселе
площадью f₁
и
при надкритическом процессе в дросселе
площадью f₂
отношение абсолют­ного
давления
p₂
в
проточной камере а
к
абсолютному входному давлению р₀
определится
отношением площадей этих дросселей f₂/
f₁.

При надкритическом
процессе в обоих дросселях имеет место

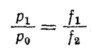
По
аналогии с электрическим потенциометром
пневмокамера называется пневматическим
потенциометром.

Схема
рассмотренного дроссельного элемента
положена в основу ряда автоматических
приборов, обладающих свойствами
пропорционального реду­цирования
(см. рис. 244, а
и
253, в).

ЭЛЕМЕНТЫ
ПНЕВМОПРИВОДОВ

Пневмодвигатели

По
принципу действия и конструктивному
выполнению элементы пневмо-систем
подобны, за исключением источников
питания, соответствующим элементам
гидросистем, а часто в обеих системах
применяются одни и те же типы
этих элементов. ‘

В
частности, преобразование энергии
сжатого воздуха в механическую работу
производится в этих системах объемными
пневмодвигателями вра­щательного
(пневмомоторы) и прямолинейного (силовые
пневмоцилиндры) движения
(рис. 227 и 3). Реже применяются пневмоповоротники
(моментные пневмоцилиндры).

Под
объемным пневмодвигателем понимается
пневмодвигатель, в котором преобразование
энергии происходит в процессе попеременного
заполнения рабочей
камеры рабочим газом и вытеснения его
из рабочей камеры.

В
качестве объемных пневмодвигателей
(пневмомоторов) вращательного движения
применяются пластинчатые и шестеренные
машины.

Устройство
и расчеты компрессоров и пневмодвигателей
были рассмо­трены
в курсе «Объемные насосы и гидродвигатели».

На
рис. 227, а
приведена
конструктивная схема типового
пластинчатого двигателя
(пневмомотора) вращательного движения.
Сжатый воздух под­водится
через канал а
корпуса,
и далее через отверстия в статоре 2 он
посту­пает
в соответствующую рабочую камеру мотора,
образованную двумя смежными
пластинами 3 и поверхностями статора 2
и ротора /, и, действуя на
эти пластины, развивает крутящий момент.
После того как камера запол­нения
отсечется при вращении ротора / от
связанных с окном питания каналов b
в
статоре, наполнение ее сжатым воздухом
прекращается. При дальнейшем вращении
ротора объем камеры увеличивается (q_x
<^ q₂)
и
рас­ширяющийся
воздух продолжает действовать на
ограничивающие ее пла­стины,
развивая крутящий момент. При соединении
камеры, заполненной частично
расширившимся воздухом, с каналами с
статора
2 воздух удаляется в
атмосферу.

Скорость
пневмомотора регулируется путем поворота
его статора 2, при
котором изменяется продолжительность
соединения рабочих камер с
отверстиями Ь
питания,
а следовательно, и степень наполнения
камер сжатым воздухом. Подобный
пневмодвигатель (пневмопривод), в котором
регулирование
производится путем отсечки потока
рабочего газа, называют пневмодвигатель
(пневмопривод) с регулированием отсечкой,
причем под отсечкой
понимается прекращение подачи рабочего
газа в рабочие камеры пневмодвигателя
в момент, когда еще происходит увеличение
их объема.

Работа
пневмомотора может протекать и при
полном расширении воздуха до
давления, близкого к атмосферному,
однако в реальных машинах приме­няется
частичное расширение, так как полное
расширение ведет вследствие значительного
понижения температуры к увеличению
размеров машины и к
обмерзанию воздушных каналов.

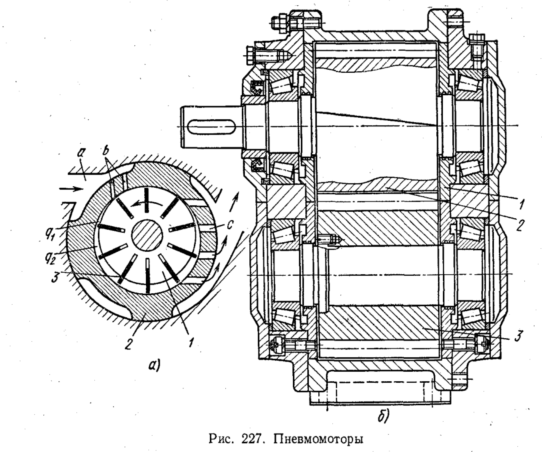
На
рис. 227, б
представлена
конструкция пневмомотора шестеренного
типа, который представляет собой пару
косозубых шестерен 2
и
3
(угол
на­клона зубьев 6—8°), валики которых
установлены на подшипниках качения.
Для
обеспечения работы в условиях плохой
смазки применены боковые диски
1
из
антифрикционного материала. Смазка
шестерен при работе пнев­момотора
осуществляется автомасленкой, подающей
масло в поток сжатого воздуха,
который через кран управления по каналам
в корпусе пневмодви­гателя
подается к блоку роторов.

В
ряде конструкций применены автоматические
устройства центробеж­ного
типа, ограничивающие максимальную
скорость пневмомотора.

На
рис. 228 показана индикаторная диаграмма
идеализированного про­цесса,
в котором наполнение цилиндра происходит
при постоянном давле­нии
р, равном магистральному, а выпуск —
при атмосферном давлении р₀.
На участке. 1—2
пути
перемещения поршня цилиндр наполняется
сжатым воздухом; в точке 2
питание
прекращается, и начинается процесс
расшире­ния воздуха (кривая 2—3
соответствует
расширению по адиабате, а кривая 2—3′
—
расширению по изотерме); в точке 3
(или
3′) цилиндр соединяется с атмосферой, и
давление мгновенно падает до атмосферного
р₀
(точка 4),
при
котором и вытесняется воздух из цилиндра;
в точке 5
цилиндр
отсоеди­няется
от атмосферы, и оставшийся в нем воздух
сжимается до давления р’;

в
точке 6
цилиндр
вновь соединяется с рабочей магистралью,
и давление в
нем мгновенно повышается до давления
р
в последней;
далее процесс повто­ряется.

Действительный
процесс отличается от описанного
идеализированного. В частности, кривая
давления наполнения не строго параллельна
оси абс­цисс,
а наклонена к ней (на рис. 228 изображена
штриховой линией). Кроме того , по ходу
поршня она колеблется. Помимо этого,
повышение давления при
заполнении цилиндра, а также понижение
при выпуске происходят не
мгновенно, а в течение некоторого
времени, которое зависит от различных
факторов,
в том числе от объема вредного пространства.

Колебания
давления в цилиндрах вызываются также
наложением про­цессов,
происходящих в соседних цилиндрах.
Последнее обусловлено тем, что
воздухораспределители обычно вы­полняются
так, что с рабочей маги­стралью
одновременно соединяются не­сколько
цилиндров, в одном из которых процесс
наполнения подходит к концу, а
в другом он лишь начинается. Оче­видно,
вследствие этого воздух перете­кает
из цилиндра с более высоким дав­лением
в цилиндр с меньшим давле­нием,
что может служить причиной колебания
среднего индикаторного дав­ления.

В
соответствий с этим идеализиро­ванная
индикаторная диаграмма дает

верхнюю
границу эффективности пневмопривода
(его максимально возмож­ную
работу) без учета потерь сжатого воздуха.
Отношение площади фактической индикаторной
диаграммы (упрощенный вид этой диаграммы
отмечен точеч­ной
штриховкой) к площади идеализированной
характеризует качество пнев-момотора
и называется коэффициентом полноты
индикаторной диаграммы.

Среднее
значение расчетного крутящего момента
пневмомотора может быть
вычислено по уравнению

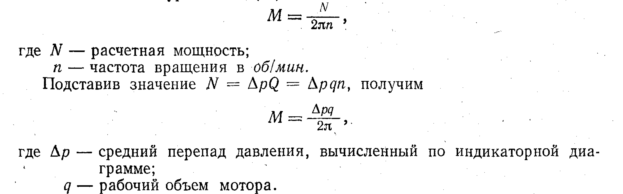
Перепад
давления можно для приближенных расчетов
принять равным высоте
прямоугольника, площадь которого равна
площади индикаторной диаграммы.

Скорость
вращения ротора пневмомотора регулируется
изменением рас­хода
сжатого воздуха с помощью дросселя,
включаемого обычно во входную магистраль,
а крутящий момент — изменением давления,
осуществляемым регулятором
(редуктором) давления.

Мембранные
исполнительные пневмомеханизмы

В
пневмосистемах, и в особенности в
пневмоавтоматике с небольшими ходами
исполнительных механизмов и давлениями
(<10 кГ/см²),
широко
распространены
пневмоаппараты, основанные на использовании
упругих элементов
(мембраны, сильфоны и пр.)- Эти аппараты
применяются как в
качестве исполнительных механизмов,
так и в качестве чувствительных элементов,
воспринимающих измеряемую величину.

В
системах промышленной пневмоавтоматики
применяются преимуще­ственно
приборы с эластичными неметаллическими
(резиновыми и пластмас­совыми)
мембранами, которые отличаются простотой
конструкции, а также возможностью
обеспечения полной герметичности.

Принцип
действия и основные расчеты этих
устройств были рассмотрены выше,
однако применительно к условиям работы
в чувствительных эле­ментах
пневмоавтоматики к мембранным устройствам
предъявляется ряд дополнительных
требований. В частности, характеристики
узлов этих пнев-моприборов
в значительной мере определяются
свойствами их упругих элементов
— эластичных мембран, определяемыми
как качеством материа- • ла,
так и их свойствами сохранять эффективную
площадь при различных условиях
работы (величинах хода, перепадах
давления и пр.).

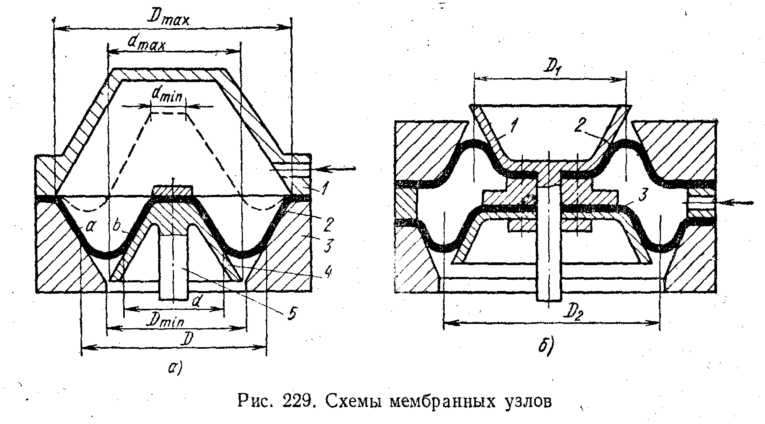
Наиболее
важным параметром является постоянство
эффективной пло­щади
мембраны _v
изменение которой является одним из
основных источников погрешностей
мембранных механизмов. Эти изменения
эффективной пло­щади
в функции изменения перепада давления
и перемещения жесткого центра
мембраны относительно плоскости ее
защемления являются основной
характеристикой мембранных пневмоприборов.
Для обеспечения высокой чувствительности
мембрана должна иметь малую жесткость
на изгиб й быть податливой при растяжении
-в окружном направлении, но должна быть
достаточно жесткой при растяжении в
радиальном направлении.

Обеспечение
заданного закона изменения эффективной
площади мембран­ного
узла. Рассмотренное
выше свойство мембран изменять свою
эффектив­ную
площадь при перемещении жесткого центра
(см. стр. 58), которое для большинства
случаев применения мембран является
отрицательным фак­тором,
поскольку оно ограничивает точность
пневмоприборов, часто исполь­зуется
для создания ряда специальных приборов
пневмоавтоматики.

В
частности, в системах пневмоавтоматики
требуется обеспечить плавное бесступенчатое
регулирование (изменение) эффективной
площади мембраны по
заданному закону.

На
рис. 229, а
изображена
схема мембранного узла, эффективная
пло­щадь мембраны которой регулируется
смещением жесткого центра. Мем­бранное
полотно 2
защемлено
по периметру между верхней 1 и нижней 3
частями
корпуса. Центральная часть полотна
зажата на грибообразном штоке
4,
который
выполняет роль жесткого центра.

Внутренняя
боковая поверхность нижней части корпуса
3
и
внешняя боковая поверхность жесткого
штока 4
выполнены
по заданному профилю (обычно
в виде усеченного прямого конуса с.
равными углами конусности при
вершине, составляющими 60°). Усилие
давления подводимого воздуха передается
на выход через шток 5
регулируемой
длины.

При
допущении, что участок свободного
провисания на дуге ab
(рис.
229, а)
очерчен
дугой круга и образующие конусов являются
каса­тельными к этой дуге, эффективная
площадь определяется текущими зна­чениями
диаметров Dud
граничных
линий касания полотна мембраны с
кони­ческими поверхностями. Последнее
обусловлено тем, что участки мембран­ного
полотна, лежащие на конических поверхностях
корпуса и жесткого центра,
в работе мембранного механизма не
участвуют, причем при равных углах
конусности дуга кривой участка провисания
сохраняется постоянной для
всех положенийжесткого центра по оси.
Однако поскольку провисание мембранного
полотна, определяющее эффективную
площадь мембраны, изменяется
при перемещении жесткого центра в осевом
направлении, изменяется с положением
этого центра также и эффективная площадь
мембраны.
Так, например, при максимальном смещении
жесткого центра из
некоторого текущего положения,
определяемого диаметрами контакта
полотна
D
и
d,
вверх
(на рис. 229, а
это
положение изображено штриховой линией)
контакт мембраны с внутренней поверхностью
конуса корпуса 3
происходит
по диаметрам D_max
j>
D
и
с внешней поверхностью конуса жест­кого
штока 4
по
диаметру основания конуса d_max
•>
d.
В
соответствии с этим эффективная
площадь мембраны достигает в этом
положении максимального значения,
определяемого из выражения

Аналогично
для крайнего нижнего положения жесткого
центра текущие значения
d
и
D
принимают
значения d_mm
<d
и D_min
<D,
причем
d_min
равно
диаметру жесткого центра, a
D_min
—
диаметру нижнего отверстия корпуса 3
(рис.
229, а).

В соответствии с
этим минимальная эффективная площадь
мембраны

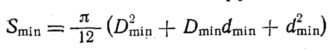
Диапазон изменения
эффективной площади

Следовательно,
минимальная и максимальная эффективная
площадь мембраны
и диапазон изменения этой площади
определяются наименьшими и наибольшими
диаметрами оснований этих конусов.

Анализ
уравнений и результаты испытаний
показывают, что эффективная

площадь
изменяется при перемещении жесткого
центра от S_min
до S_max
по

параболе
(вытяжкой полотна мембраны пренебрегаем).
Соответственно жест­

кость
мембраны, характеризуемая функцией S
— f
(х), где
х
—
перемещение

центра,
находится для рассматриваемой схемы и
условий в линейной зави­симости от
положения жесткого центра относительно
его крайнего нижнего

положения.

Для
расширения диапазона изменения
эффективной площади мембран­ного
прибора применяют схемы с двумя
мембранами, соединенными с общим жестким
центром в виде двух усеченных прямых
конусов равной конусности, вершины
которых обращены друг к другу (рис. 229,
б).

Нетрудно
видеть, что усилия, развиваемые этими
мембранами при подаче воздуха
в камеру, направлены в противоположные
стороны, ввиду чего эффективная
площадь такой двухмембраннои коробки
равна разности эффек­тивных площадей
ее мембран, которые определяются, как
и в ранее рассмот­ренной
схеме, текущими эффективными диаметрами
D₁
и
D₂.

В
соответствии с этим с помощью такой
двухмембранной коробки можно получить
как нулевую, так и отрицательную
эффективную площадь мем­браны,
т. е. усилие такого механизма может
изменить свой знак. При пере­мещении
общего центра 1
мембран
вниз эффективная площадь нижней мем­браны
3
уменьшается,
а верхней 2 — увеличивается. Поскольку
эффектив­ная
площадь всей мембранной коробки в этой
схеме равна разности эффек­тивных
площадей мембран 2 и 3, то при некотором
положении жесткого центра /, в котором
площади мембран равны, результирующая
эффективная площадь
равна нулю. При дальнейшем смещении
жесткого центра в том же направлении
эффективная площадь верхней мембраны
2
станет
больше, чем нижней 3
(эффективная
площадь станет «отрицательной»), в
соответствии с
чем изменится знак усилия на штоке.

Анализ
показывает, что эффективная площадь
такой мембранной коробки практически
находится в линейной зависимости от
перемещения ее жесткого центра,
и следовательно, она обладает постоянной
жесткостью.

Распределительная
и регулирующая аппаратура пневмосистем

В
пневмосистемах применяется распределительная
и регулирующая аппа­ратура
тех же типов и конструктивных исполнений,
что и в гидросистемах, и
лишь в отдельных случаях применяются
дополнительные средства для повышения
герметичности и обеспечения смазки.
Так, например, повсе­местно
применяются распределительные и прочие
регулирующие клапаны с дополни­тельными
средствами герметизации в виде резиновых
уплотнительных колец, а также клапаны
с эластичными затворами.

Распределительные
клапаны. Для
распре­деления
воздуха применяются двухпозици-онные
клапаны и золотники с плоскими
распределительными
элементами, которые обеспечивают
высокую герметичность сое­динения.

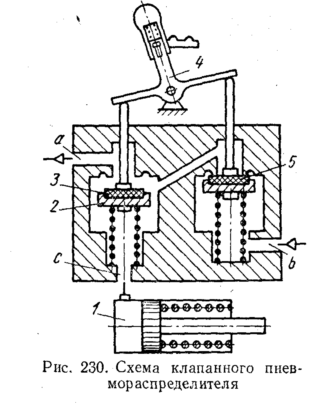
На
рис. 230 приведена принципиальная схема
клапанного распределителя для управ­ления
пневмоцилиндром одностороннего действия.
Подвод сжатого воздуха произво­дится
к каналу Ь,
а
отвод отработавшего воз­духа—
через канал а.
Рабочая
полость сило­вого цилиндра / соединена
с каналом с. При повороте рычага 4
утапливается
тот или иной клапан 2 или 5, в результате
воздух или подводится в рабочую полость
цилиндра 1,
или
отводится из него в атмосферу. Герметизация
затворов клапанов осу­ществляется
плоскими или резиновыми фторопластовыми
кольцами’З, заде­ланными
в металлические части затворов.

Клапан
управляется вручную различными рычагами
и толкателями, а
также электромагнитами и сжатым воздухом,
причем при отсутствии управляющего
воздействия затвор клапана обычно
перекрывает под воздей­ствием пружины
проход воздуха от подводящего к выходному
отверстию.

На
рис. 231 представлены клапаны с ручным
воздействием на толкатель 2, осуществляемым
через рычаг / (рис. 231, а), и механическим
воздействием на этот толкатель (рис.
231, в).

Сжатый
воздух (давление до 6 кГ1см^г)
подводится
к каналу Ъ
(рис.
231, а).
В
положении затвора клапана 4,
показанном
на рис. 231, а
(толкатель
2
не
нажат), он усилием пружины 5
к
давления сжатого воздуха прижимается
к седлу втулки 6
и
герметично перекрывает с помощью
резиновой прокладки 3

проход
воздуху от входного отверстия Ь
к
отверстию а,
которое
сообщается через
осевое сверление толкателя 2
с
атмосферой. При утапливании (переме­щении
вправо) толкателя 2
он
упирается сначала:своим торцом в
резиновую прокладку 3
затвора,
отключая отверстие а
от
атмосферы, и при дальнейшем перемещении
отрывает затвор клапана 4
от
седла, открывая при этом проход сжатому
воздуху от входного отверстия b
в
отверстие а
пневмодвигателя.

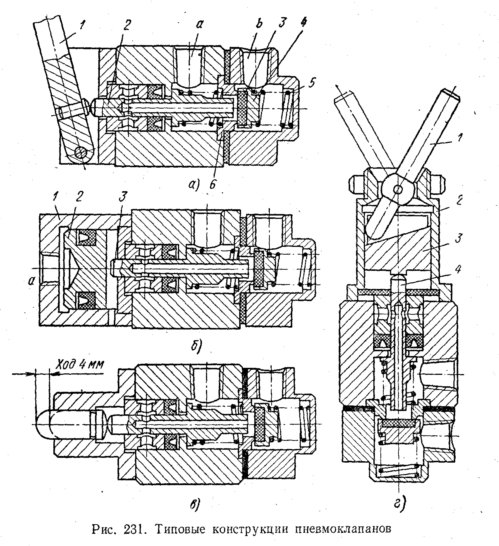
На
рис. 231, б
показан
клапан с пневматическим воздействием
на тол­катель 3
через
поршень 2
пневмоциливдра
1.
Сжатый
воздух подается в ка­нал
а.

В
тех случаях, когда требуется обеспечить
фиксирование затвора в обоих крайних
его положениях, применяются различные
механические средства. В
клапане, представленном на рис. 231, г,
это
обеспечивается тем, что рычаг 1
воздействует
на толкатель 4
через
перемещающуюся в направляющих 2
косую
шайбу 3,
с
помощью которой рычаг / фиксируется в
обоих крайних своих положениях.
Эта фиксация обеспечивается тем, что в
обоих крайних поло­жениях
рычага / усилие реакции подпружиненной
косой шайбы 3
стремится
удержать
его в этом положении.

Пневмоклапаны
с электромагнитным управлением. В
системах пневмо­автоматики
широко применяются распределительные
клапаны с электро­магнитным
управлением.

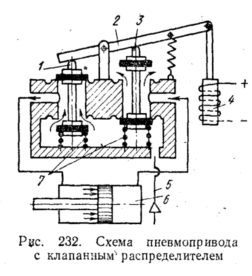
На
рис. 232 приведена принципиальная схема
пневмопривода с распреде­лением
плоскими клапанами с резиновыми
затворами. Открытие (утапли-вание)
клапанов 1
и 3 осуществляется
электромагнитом 4
через
рычаг 2
и

закрытие
— пружинами 7. При утапливании левого
клапана / и освобожде­нии правого
клапана 3
левая
полость пневмоцюшндра 6
соединяется
с маги­стралью 5
питания
сжатым воздухом, а правая — с атмосферой
и наоборот. Применяются
клапаны прямого действия и с серводействием
(двухсту­пенчатые
клапаны).

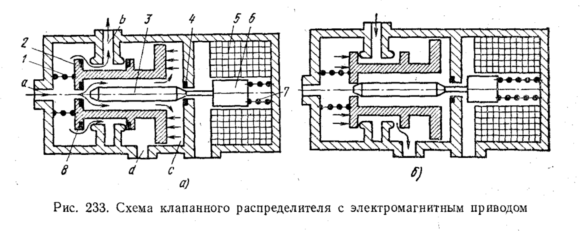
На
рис. 233, а
приведена
схема двухпозиционного клапанного
распреде­лителя
(пневмокрана) с электромагнитным
сервоприводом.

Запорный
узел этого распределителя со­стоит
из двух клапанов (затворов), один из
которых
2,
нагруженный
пружиной 1,
является
собственно распределителем, а вто­рой
3, связанный с якорем 6
электромагнита
5,
—
вспомогательным клапаном (клапаном-пилотом),
управляющим основным клапа­ном
2.

При
подаче напряжения на обмотку элек­тромагнита
5
его
якорь 6
переместится,
преодолевая усилие пружины 7 вправо, в
ре­зультате правый затвор вспомогательного
клапана 3
сядет
на седло 4,
отойдя
от седла 8,
выполненного
в основном клапане 2
(рис.
233, а).
При
этом воздух под давлением поступит
в камеру с
и,
действуя на пра­вый
торец основного клапана 2, переместит

его
влево, соединив канал питания а
с
каналом потребителя Ь
и
перекрыв одновременно
проход к каналу d,
ведущему
в атмосферу.

После
обесточивания обмоток электромагнита
5
его
якорь 6
под
действием пружины 7
переместится
влево, в результате связанный с ним.затвор
вспомо­гательного клапана 3
отойдет
от седла 4
и
соединит камеру с
с
атмосферой. Это позволит пружине 1
возвратить
основной клапан 2
в
исходное (правое) положение (рис. 233, б).
При
этом клапан 3
сядет
на седло 8, перекрывая доступ
воздуха из канала питания а
в
камеру с.

Золотники
с плоским распределительным элементом.
Распространены
пневмораспределители
с плоским распределительным элементом
(золотни­ком),
которые выполняются с различным (ручным,
пневматическим и элек­трическим)
управлением.

Конструктивно
эти золотники подобны аналогичным
золотникам гидро­систем.

Управление
этими распределителями осуществляется,
как правило, с по­мощью
пневматических устройств или
электромагнитов.

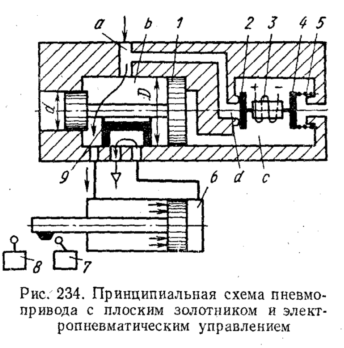
На
рис. 234. показана принципиальная
пневмосхема с электропневмати­ческим
распределителем в виде плоского золотника
9
(см.
также рис. 54),

приводимым
связанным с ним дифференциальным
плунжером 1 (диаметр D>d).

Командными
элементами в этой схеме являются концевые
выключа­тели
7
и
8,
на
которые воздействуют упоры, установленные
на штоке сило­вого пневмоцилиндра 6.
Исполнительным
элементом является сердечник электромагнита
3,
несущий
управляющие пневмоклапаны 2
и
4, отжимаемые
пружиной 5 в левое положение, в котором
клапан 2 перекрывает канал d,
соединенный
с межпоршневой камерой b
и
вводным каналом а.

При
втягивании сердечника в катушку
пневмоклапан 4
отсоединяет
камеру с от атмосферы, а клапан 2 соединяет
ее с каналом пневмосети, в ре­зультате
сжатый воздух, воздействуя на
дифференциальный плунжер 1, перемещает
плоский золотник 9
в
левое положение, в соответствии с чем
поршень пневмоцилиндра 6
переме­щается
влево.

В
конце хода штока пневмоцилин­дра
6
им
приводится в действие выклю­чатель
<§, который обесточивает элек­тромагнит
3,
в
результате клапан 4
соединяет
камеру с
с
атмосферой, а клапан
2
перекрывает
канал d,
соеди­няющий
ее с камерой Ъ
между
диффе­ренциальными
поршнями распредели­тельного
плунжера 1.
При
этом плун­жер вместе с золотником 9
в
результате действия на его поршни
неуравновешенного вследствие
разности площадей давления
в камере перемещается вправо (в
положение, показанное на рис. 234), соединяя
левую полость пневмоцилинд-ра
6
с
каналом а
питания.
В резуль­тате шток пневмоцилиндра 6
возвратится
в исходное положение, воздей­ствуя в
конце своего хода на выключатель 7. Далее
цикл повторится.

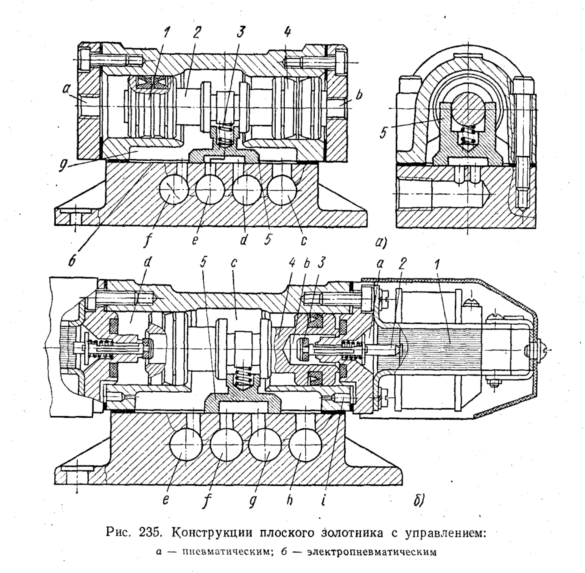
На
рис. 235, а
представлена
конструкция золотника с двусторонним
пнев­матическим
управлением прямого действия.

Плоский
золотник 5
перемещается
из одного крайнего положения в дру­гое
поршнями 1
и 4, общий
шток 2 которых механически связан с
золотни­ком. К зеркалу корпуса 6
распределителя
золотник 5
прижимается
усилием пружины 3
и
давлением’ воздуха в камере g,
соединенной
с каналом с питания.

Сжатый
воздух подводится к каналу с
и
отводится в атмосферу через канал
е.
Перемещение
золотника осуществляется давлением
сжатого воз­духа,’подводимого
поочередно в цилиндры двустороннего
поршня от какого-либо
источника через отверстия а
и
Ъ.

В одном
из крайних положений золотника 5
сжатый
воздух проходит к отверстию f,
связанному с одной из полостей
пневмоцилиндра, а отвер­стие d
в
это время сообщается с атмосферой. В
другом крайнем положении золотника
отверстие f
сообщается с атмосферой, а отверстие d
второй
полости пневмопривода — с магистралью
сжатого воздуха. Следовательно, отвер­стия
f
и d,
соединенные
с полостями силового пневмоцилиндра,
сообщаются попеременно при перемещении
золотника 5 либо с каналом питания, либо
с
атмосферой. Необходимо учесть, что
золотник в этой схеме распределения
будет нагружен давлением воздуха,
действующим на всю омываемую им
поверхность.

На
рис. 235, б
показана
конструкция двухпозиционного
четырехходо-вого
воздухораспределителя этого типа с
двусторонним электропневматиче­ским
управлением. Сжатый воздух подводится
к внутренней полости с
воздухораспределителя
через входное отверстие h
и
далее в зависимости

от
положения золотника 5
поступает
к соответствующим каналам е
или
g,
свя­занным
с полостями пневмоцилиндра.

На
рис. 235, б
правый
электромагнит / показан во включенном
поло­жении, а левый — в выключенном.

Якорь
правого электромагнита, втягиваясь,
нажимает на стержень 2
клапана
управления, открывая затворы. Сжатый
воздух из полости с
через
отверстие
I
малой
площади сечения (дроссель) поступает в
полости dub
под
торцы поршня 4.
При
включенном правом электромагните
стержень 3 вместе
с резиновой прокладкой отодвигается
влево, открывая выход сжатому воздуху
из полости b
через
отверстие а
в
атмосферу.
В результате давление воздуха в полости
b
падает,
тогда как в полости d
оно
равно подводимому, ввиду чего поршень
4
с
золотником 5
перемещается
в правое положение. В
этом положении золотника сжатый воздух
из полости с поступает в отвер­стие
е,
а
отверстие g
сообщается
с атмосферой через отверстие f.
При
этом поршень 4
кольцевым
выступом (рыльцем) упирается в резиновую
про­кладку 6
и
‘закрывает выход сжатому воздуху через
отверстие а
в
атмосферу в
течение всего времени, пока электромагнит
включен.

При
выключении правого электромагнита
стержень (затвор клапана) 3
возвращается
в исходное положение.

При
включении левого электромагнита полость
d
соединяется
с атмосфе­рой и поршень 4
вместе
с золотником 5
переместится
влево. При этом сжатый воздух из полости
с поступает в отверстие g,
а
отверстие е
сообщается
с атмо­сферой через отверстие f.

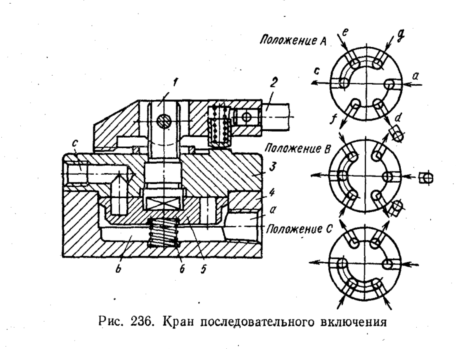
Краны
последовательного включения. Для
последовательного включения двух
силовых пневмоцилиндров при движении
их штоков в одном направле­нии
и для одновременного возвращения в
другом направлении, что часто требуется
в пневмоприводах станков и других машин,
применяются много­позиционные
поворотные золотники (краны) с плоским
распределительным элементом.
Распределитель (рис. 236) представляет
собой трехпозиционный шестиходовой
кран с ручным управлением. Сжатый воздух
подводится к
крану через канал а
к
внутренней полости b
крана,
образованной корпу­сом 4
и
крышкой 3,
и
отводится в атмосферу через канал с. К
зеркалу крышки 3
прижимается
давлением сжатого воздуха и
пружиной
6
плоский
золотник 5,
поворот
которого производится с помощью валика
1 и ру­коятки 2,
имеющей
три фиксированных положения, в которых
каналы рас­пределителя d,
e,
f
и
g,
ведущие
к полостям управляемых пневмоцилиндров
(двигателей),
сообщаются попеременно с полостью
давления или с атмосфе­рой.
В положении А
входной
канал а
соединяется
с каналами d
и
/ и выход­ной канал с
с
каналами е
и
g;
при
повороте крана против часовой стрелки
(в положение В)
входной
канал а
соединен
с каналами d
и
g,
а
при повороте крана
по часовой стрелке (положение С) входной
канал соединен с кана­лами
g
и
е.

Регулирование
скорости пневмодвигателя и схемы
управления. Регули­рование
скорости пневмодвигателя осуществляется
устройствами, приме­няемыми
в гидродвигателях.

Скорость
рабочего органа обычно регулируется
дроссельным регуля­тором
скорости, устанавливаемым на выходе
двигателя (см. рис. 102, б).
При
колебаниях нагрузки в этом случае, а
следовательно, и скорости пере­мещения
выхода изменяется противодавление в
нерабочей (выпускной) полости,
которое сглаживает колебание скорости
(повышает плавность движения).

Для
поддержания заданного режима применяются
как ручные, так и автоматические
устройства, регулирование которых
осуществляется в боль­шинстве
случаев в функции давления или пути;
реже применяется управ­ление
в функции времени.

При
путевом управлении команды на срабатывание
пневмоцилиндра поступают
от управляющих клапанов, которые
переключаются в соответствующем
месте хода движущимся элементом
пневмоцилиндра или иной подвижной
частью машины.

Схема
пневмопривода с таким управлением
приведена на рис. 237, а.
Элементы
пневмосистемы показаны в исходном
положении, т. е. в положе­нии,
предшествующем началу цикла. Система
имеет пусковой клапан 5
и
два клапана 1
и
3,
управляемые
упором 2 на штоке пневмоцилиндра 4,
через
которые производится питание сервопривода
плоского распределитель­ного
золотника 6.
Перемещение
последнего обеспечивается сбросом
давления из
соответствующей (правой или левой)
полости цилиндров сервопривода. Для
этого сжатый воздух постоянно подводится
через дроссельные отвер­стия
а
в
поршеньках плунжера золотника 6
в
обе полости цилиндров (серво­привода)
управления этим золотником.

Система
приводится в действие вручную при помощи
пускового кла­пана
5, при перемещении которого вниз левая
полость цилиндра золот­ника 6
соединяется
через открывшийся клапан 5
и
через открытый упором 2 на штоке клапан
3
с
атмосферой, в результате давление в
левой полости пневмоцилиндра 4
понизится
практически до атмосферного. Поскольку
же клапан 1 при этом остается закрытым,
давление в правой полости цилиндра
золотника 6
будет
равно давлению в сети, и плунжер золотника
под действием перепада
давления переместится влево. При этом
сжатый воздух будет под­водиться
в левую полость пневмоцилиндра 4,
а
отработавший — удаляться в
атмосферу. Под действием сил давления
сжатого воздуха поршень сило­вого
пневмоцилиндра 4
будет
перемещаться вправо. При этом при отходе
упора 2 от клапана 3
последний
под действием внутренней пружины
пере­местится
влево, отсоединив правую полость
приводного цилиндра золот­ника
6
от
линии питания и соединив эту полость с
атмосферой.

В конце
прямого хода штока упор 2 приведет в
действие клапан 1,
откры­вая
выход сжатому воздуху из правой полости
цилиндра управления золот­ника 6,
в
результате произойдет переключение
его в положение обратного хода штода
пневмоцилиндра 4.
По
окончании этого хода цикл повторится.
Сопротивление дроссельных отверстий
а
в
поршеньках золотника 6
должно
быть
возможно большим (значительно выше
сопротивления трубопровода и
клапанов 1
и
3).

Управление
в функции времени. Управление
пневмоприводом в функции времени
характеризуется тем, что сигналы подаются
через заданные в соот­ветствии
с технологическим процессом промежутки
времени, что дости­гается
с помощью командоаппаратов и устройств
(реле), отсчитывающих длительность
операций.

На
рис. 237, б
показана
схема пневмопривода станка, управляемого
с
помощью установленного на валу
командоаппарата или иной части станка,
вращающегося
кулачка 3,
скорость
вращения которого определяет длитель­ность
цикла. При утапливании кулачком 3
клапана
/ сжатый воздух из сети поступает в
правую полость распределителя 2 с
дифференциальным привод­ным поршнем
(d₁
>>
d₂),
перемещая
его в положение, соответствующее
рабо­чему ходу штока пневмоцилиндра
4.
При
снятии сигнала управления плун­жер
распределителя 2
давлением
жидкости в левой его полости возвращается
в
исходное (правое) положение.

Торможение
пневмоприводов.
Во многих случаях применения пневмо­привода
оказывается необходимым осуществить
торможение поршня пневмо-

цилиндра
в конце его движения для избежания
удара, который нежела­телен
или недопустим по условиям прочности
механизмов или характера технологической
операции.

Торможение
осуществляется внутренним или внешними
дроссельными тормозными
устройствами, устанавливаемыми на пути
отвода воздуха из полости
опорожнения (нерабочей полости). Эти
устройства уменьшают проходное
сечение выходной (отводной) магистрали
в некоторой точке хода поршня
пневмоцилиндра, в результате в этой
полости создается тормозное противодавление,
снижающее скорость движения поршня.

На
рис. 238, а
показана
схема пневмоцилиндра с подобным
устрой­ством.
Питание цилиндра и движение его поршня
происходит по обычной схеме
до того, пока соответствующий выступ а
на
поршне / не перекроет одну из камер Ь.
После
же того как поршень 1
цилиндра
перекроет при
движении, например влево, своим выступом
а
камеру
Ь,
диаметр
d₂
которой
равен диаметру &_х
выступа,
воздух сможет удаляться из выпускной
полости (в данном случае — правой) лишь
через регулируемый дроссель 3 малого
сечения, в результате воздух в этой
полости сжимается, тормозя
движение с интенсивностью, определяемой
регулировкой дросселя.

В
исходное (левое) положение поршень
возвращается после переключе­ния
управляющего пневмораспределителя под
воздействием воздуха, про­текающего
в правую полость в обход дросселя через
обратный клапан 2.
В
конце хода поршня вступает в действие
тормозная система левой полости цилиндра.
Кинетическая энергия движущихся масс
привода преобразуется при
торможении в работу сжатия воздуха. Эта
работа определяется коли­чеством
сжимаемого в полости цилиндра воздуха
и степенью его сжатия (отношением
противодавления в цилиндре в конце и
начале торможения), а
также характером процесса сжатия (см.
стр. 260).

Недостатком
внутренних тормозных устройств является
трудность регу­лировки
момента включения их по ходу поршня,
ввиду чего в случае необ­ходимости
подобной регулировки применяют внешние
тормозные устрой­ства.
На рис. 238, б
показана
схема привода с внешним тормозным
устройством. Система снабжена
четырехходовым распределителем 2
и
трехходовым распределителем 5,
управляемым
с помощью кулачка 6
на
штоке поршня 1
пневмоцилиндра
и снабженным регулятором скорости. При
перемещении поршня 1
вправо
сжатый воздух отводится через трехходовой
5 и четырех-ходовой 2 распределители в
атмосферу. В определенном (заданном)
месте хода шток поршня при помощи кулачка
6
переключает
(утапливает) распре­делитель 5, в
результате воздух будет выходить лишь
через регулируемый дроссель 4,
ввиду
чего обеспечивается снижение скорости
поршня до тре­буемой
величины.

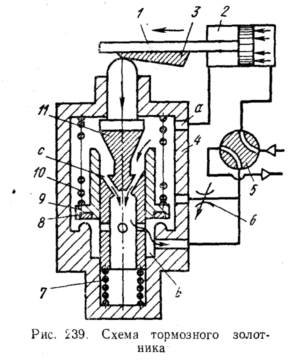
В
начале обратного хода поршня (влево)
подача сжатого воздуха проис­ходит
до того, как распределитель 5
еще
не переключен (находится в утоп­ленном
положении), через распределитель 2 и
обратный клапан 3
и
после

прекращения
действия кулачка 6
на
рас­пределитель 5
—
непосредственно минуя дроссель (регулятор
скорости) 4.
Распре­делитель
5, обратный клапан 3
и
дрос­сель 4
обычно
комплектуются в одном агрегате,
получившем название тормоз­ного
клапана. При помощи этого клапана могут
быть обеспечены как требуемая степень
дросселирования в конце хода по­ршня,
так и изменение длины тормозного пути
и скорости перемещения на любом участке
пути.

Для
торможения движения штока пнев­моцилиндра
путем дросселирования пото­ка
воздуха, удаляемого из опоражнивае­мой
полости цилиндра, применяют также
специальные
тормозные золотники, кото­рые
позволяют затормозить приводимый
рабочий
орган (по заданному закону) в любом
месте его пути.

Схема
подобного золотника пока­зана
на рис. 239. Золотник состоит из
дроссельного плунжера 11
с
конусным

затвором,
управляемого упором (кулачком) 3
на
движущейся части (штоке 1
пневмоцилиндра
2)
машины,
и свободно посаженного запорного клапана
9,
нагруженного
пружиной 10.
Плунжер
И
в
свободном состоя­нии удерживается
пружиной 7 в верхнем положении, в котором
между конусным затвором плунжера 11
и
гильзой клапана 9
образуется
щель, ло
которой воздух из опоражнивающейся
(нерабочей) полости пневмоци­линдра
2 сбрасывается через отверстия с,
камеру
Ь
и
распределительный кран 5 в атмосферу.
В этом случае шток 1
пневмоцилиндра
2 пере­мещается
со скоростью, определяемой начальным
положением плун­жера
11.

На
соответствующем (заданном) участке пути
упор 3, связанный со што­ком 1
пневмоцилиндра,
нажимает на плунжер 11
и,
сжав пружины 7, пере­мещает
его вниз. При этом плунжер И
своей
конусной частью заходит в
отверстие хвостовика клапана 9,
в
результате площадь проходного сечения
щели d
с
перемещением плунжера И
уменьшается,
что вызывает повышение противодавления
в опоражниваемой полости пневмоцилиндра
2
и
плавное затормаживание штока /. После
того как плунжер 11
полностью
перекроет проходную щель, воздух из
опорожняемой полости пневмоцилиндра
2 вы­тесняется лишь через регулируемый
дроссель 6,
настройкой
которого регулируется скорость штока
/.

При
реверсировании распределительного
крана 5 сжатый воздух из маги­страли
подается в полость Ь.
Преодолевая
усилие слабой пружины 16,
воздух
откроет клапан 9
с
уплотняющей прокладкой 8
и
направится в пек лость, откуда через
отверстие а
поступит
в левую полость пневмоцилиндра 2. Таким
образом обеспечивается при реверсировании
беспрепятственное напол­нение
пневмоцилиндра сжатым воздухом, несмотря
на то, что дроссельный плунжер
11
еще
остается в течение некоторого времени
в утопленном поло­жении.

Плавность
торможения и его продолжительность
определяются длиной и
профилем нажимного кулачка 3,
воздействующего
на дроссельный плун­жер 11.

Гидравлические
демпферы. Вследствие
сжимаемости воздуха обеспечить при
пневматическом демпфере строго заданный
закон торможения и гаран­тировать
остановку поршня точно в
крайнем положении практически невозможно.
Ввиду этого в случае повышенных
требований к тормо­жению
применяют гидравлический демпфер.

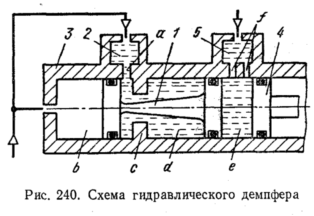
На
рис. 240 показана схема од­ного
из таких демпферов. Демпфер состоитиз
конусного штока 1
сдвумя
поршнями,
межпоршневая камера d
которого
заполнена тормозной жидкостью.
Поршень давлением воздуха
в левой полости Ъ,
соеди­ненной
с воздушной магистралью, постоянно
удерживается в крайнем правом положении.
Поскольку с этой же
магистралью соединен и бачок 2,
под
таким же давлением будет нахо­диться
до вступления демпфера в действие и
тормозная жидкость в камере
d.

После
того как поршень 4
силового
пневмоцилиндра при перемещении влево
придет в контакт с правым тормозным
поршнем и приведет его в дви­жение
в том же направлении, жидкость из камеры
d
вытесняется
через дрос­сельное кольцевое проходное
сечение, образованное штоком 1
и
отверстием в
перегородке
с, в правую полость тормозного цилиндра
3
(в
камеру а).
Поршневой
шток 1
обычно
выполняется в виде конуса, подбором
конусности которого
можно обеспечить требуемую эффективность
и закон торможения. Расчеты
показывают, что при конусном штоке /
практически обеспечивается закон
равномерного замедления поршня 4.

Обратное
движение поршня 4
пневмоцилиндра
осуществляется через жидкость, находящуюся
в бачке 5, в который для этого подводится
через распределитель
воздух под давлением.

Рассматриваемая
схема предотвращает также жесткий удар
поршня 4
при
подходе его при прямом ходе к правому
поршню штока 1.
Из
схемы сле­дует, что при движении поршня
4
влево
он вытесняет через отверстия / жидкость
из промежуточной камеры е
в
бачок 5.
После
того как первое из отверстий / будет
перекрыто движущимся поршнем 4,
эффективность
демпфирования повысится, а после
перекрытия и второго отверстия поршень
4
и
шток 1
будут
связаны жидкостью, запертой в камере
е.
Благодаря
этому устройству
обеспечивается плавность включения
демпфирующего устрой­ства.

Пневматический
регулятор.
В
машиностроении широкое применение
получили автоматические пневматические
регуляторы расхода, схема одного из
которых приведена на рис. 241.

Изменение
регулируемого параметра (расхода
воздуха, протекающего по
магистрали 14)
передается
в виде сигнала (изменения давления)
датчику 4,
который
перемещает заслонку 6
регулятора,
изменяя расстояние (зазор) х
между
срезом сопла 5
и
заслонкой. В результате изменяется
давление р₁

в
предсопловой камере Ь
и
в камере с сильфона 8,
причем
при уменьшении расстояния
х
давление
р₁
повышается
и наоборот. В соответствии с этим
изменяется
также и давление р₂
на
выходе из регулятора, которое и служит
давлением
среды, питающей исполнительный механизм
(в данном случае мембранный
привод 15
перекрывного
вентиля магистрали 14).
Давление
р₂
действует
также на второй сильфон 7,
площадь
которого меньше площади сильфона 8.

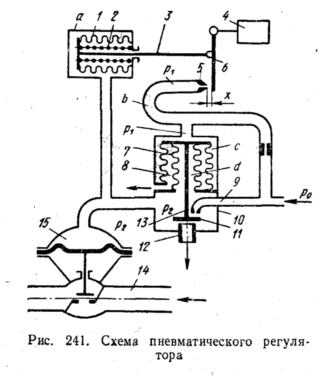
Для
обеспечения равновесного состояния
процесса при разных величинах регулируемого
параметра в схему регулятора включена
обратная связь, состоящая
из камеры а
с
сильфоном 1
и
пружины 2. В камеру а
передается

давление
р₂
регулируемого
(команд­ного) потока воздуха, которое
воз­действует
на сильфон / и перемещает с помощью штока
3
заслонку
6,
сни­жая
входной сигнал датчика 4.

В
данной схеме сопло—заслонка 5—6
является
усилителем сигнала, поступающего в
сильфонный датчик а
(усилитель
первой ступени), а силь-фонная
коробка 10
—
усилителем второй
ступени, повышающим с по­мощью
регулируемого дросселя И—
12
давление
воздуха с р_г
до
р₂
на входе
в исполнительный механизм.

Рассмотрим
действие сильфонной коробки
10,
являющейся
усилителем второй
ступени. Сжатый воздух под давлением
р₀
через
регулируемый дроссель
типа сопло—заслонка 9—//
поступает в сильфонную камеру d,
соединенную
с одной стороны с поло­стью
мембранного привода 15
и
одно­временно
через второй регулируе­мый
дроссель, состоящий из той же заслонки
// и трубки 12,
с
атмос­ферой. Заслонка // стержнем
связана с сильфонной коробкой, вследствие
чего расстояние ее от среза сопла 9
и
торца дренажной трубки 12
опреде­ляется
давлением р_г
усилителя
первой ступени (давлением перед соплом
5). При перемещении заслонки 11
вниз
увеличивается проходное сечение между
ею и соплом 9
и
одновременно уменьшается сечение
торцовой щели между заслонкой и трубкой
12.
При
полном перекрытии заслонкой 11
проходного
сечения трубки 12
в
камере d,
а
следовательно, и в мембран­ном приводе
15
установится
максимальное давление.

Равновесие
сильфонного датчика определится
равенством

где
F₁
и F₂
— эффективные площади сильфонов 7
и 8. Ввиду
того что F₁>F₂
будем
иметь р₂
> р₁.

Регулятором
этого типа обеспечивается с большой
степенью точности линейная
зависимость между изменением регулируемого
параметра и выход­ным
давлением р₂,
т. е. перемещением исполнительного
мембранного при­вода перекрывного
вентиля магистрали 14.
Иначе
говоря, каждому значе­нию
регулируемого параметра соответствует
строго определенное значение давления
р₂
в мембранном приводе.

Аппараты
регулирования давления воздуха. Для
нормальной работы пневмосистемы
питание ее должно производиться воздухом
с постоянным давлением,
которое обеспечивается специальными
регуляторами давления (редукторами
давления или редукционными клапанами).

Редуктор
давления — регулятор, служащий для
автоматического пони­жения
давления сжатого воздуха и автоматического
поддержания его на заданном уровне.

В
качестве редукторов применяются
преимущественно диафрагменные (см.
рис. 72, 6)
и
сильфонные (см. рис. 73) их типы. Эти
редукторы исполь­зуются для получения
относительно невысоких давлений (до
30—40 кГ/см²)
вследствие
ограниченной прочности диафрагмы и
сильфона.

Затвор
в клапанах, предназначенных для работы
с газами, выполняют обычно
в виде плоского (пластинчатого)
обрезиненного или изготовленного из
эластичного материала клапана, сажаемого
на гнездо с закругленными выступающими
кромками (реже применяются шариковые
затворы).

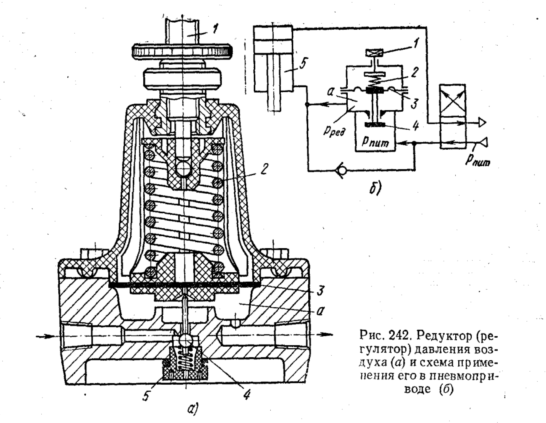
На
рис. 242, а
показан
один из аппаратов этого назначения,
который в практике получил название
стабилизатора (редуктора) давления (см.
также рис. 72, б). Принцип его работы
основан на автоматическом изменении
проход­ного
сечения потока воздуха при изменении
давления и расхода воздуха в
питающей сети и поддержании, таким
образом, постоянства давления воз­духа
на выходе стабилизатора (в линии
потребителей). Постоянство давле­ния
обеспечивается автоматическим изменением
положения дроссельного клапана,
регулирующего проходное сечение потока
воздуха при колеба­ниях
давления в камере а,
связанной
с выходом.

Для
установки требуемого рабочего давления
на выходе стабилизатора служит
регулировочный (дроссельный) винт /, с
помощью которого изме­няют усилие
пружины 2,
воздействующей
на мембрану 3,
связанную
с кла­паном 4,
который
удерживается в седле пружиной 5. Изменение
давления и расхода воздуха в сети
вызывает перемещение мембраны 3
и
клапана 4,
вследствие
чего изменяется проходное сечение
потока воздуха до тех пор, пока
силы, воздействующие на мембрану 3,
не
уравновесятся и давление в
камере а
не
стабилизируется.

При
уменьшении давления в камере а,
что
может быть вызвано уменьше­нием
давления в подводящей сети или увеличением
расхода воздуха потре­бителями,
мембрана 3
под
действием пружины 2
опустится
и, переместив

вниз
клапан 4,
увеличит
проходное сечение потока воздуха, что
обеспечит выравнивание
давления в камере а
до
заданного.

Увеличение
давления в камере а
вызовет
обратное действие указанных частей
стабилизатора. Малейшее изменение
давления в камере а
вызовет
мгновенное
изменение положения клапана 4.

На
рис. 242, б
изображена
схема пневмосистемы с диафрагменным
регу­лятором,
установленным в магистрали питания
щтоковой (нижней) полости пневмоцилиндра
5, давление в которой должно быть ниже
давления р_пит

в
магистрали питания (р_ред
<
р_пит).

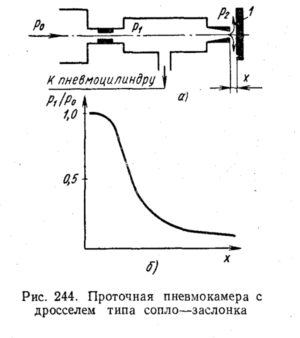
При
повышении давления р_ред
воздуха
на
выходе из регулятора (в камере а)
мембрана
3
прогибается
вверх, и, преодо­левая усилие пружины
2
и
перемещая вверх плоский затвор клапана
4,
уменьшает
проходное его сечение. При понижении
же давления на выходе проходное сечение
клапана увеличи­вается.
Настройка регулятора на требуемое
давление осуществляется винтом 1,
сжимающим
пружину 2.

Пропорциональное
редуцирование давления. В системах
пневмоавтома­тики
применяют также приборы регулирования
давления, обладающие свой­ством
пропорционального редуцирования
(редуцирования давления в задан­ном
отношении), которое достигается
применением последовательно соеди­ненных
двух и более дросселей в сочетании с
редукционным клапаном.

Принципиальная
схема подобного регулятора приведена
на рис. 243, а.
Регулятор
состоит из двух камер аи Ь,
разделенных
мембраной 2, связанной с редукционным
клапаном 5,
установленным
в верхней камере Ь.
На
входе в нижнюю проточную камеру а и на
выходе из нее установлены дроссели / и
3
постоянного
сопротивления. На выходе из верхней
камеры установлен дроссель
4.

В
нижней камере действует давление р₁
определяемое неравенством Po>Pi>P2,
где

Р_о
— давление перед дросселем 1 и р₈
— давление после дросселя 3.

Выбором
сечений этих дросселей f_t
и
f₃
устанавливается требуемое дав­ление
р! в нижней камере а,
которое
поддерживается также и в верхней
надмембранной
камере (считаем мембрану абсолютно
эластичной), выбо­ром
же сечения f₄
Дросселя на выходе из верхней камеры
регулируется рас­ход воздуха через
редукционный клапан 5.

Расчет
рассматриваемого регулятора сводится
к расчету заполнения и опорожнения
камер (емкостей) а
и
Ь
через
дроссели /, 3,
4. Анализ
пока­зывает, что отношение р_г/р₀
давлений
р_х
в
камере а
и
р₀
—
на входе в эту камеру определится
отношением площадей дросселей /₃//_lt
причем при над­критическом
процессе истечения в обоих дросселях
имеем

По аналогии с
электрическим потенциометром рассмотренную
камеру обычно называют пневматическим
потенциометром.

На
этом же принципе построен также и
аналогичный датчик отношения давления
p₀/p₁,
схема
которого представлена на рис. 243, б.

Проточная
камера с выходным регулируемым дросселем
типа сопло— заслонка
широко применяется, в частности, в
пневмогидравлических сле­дящих
приводах в качестве первой ступени
усиления (рис. 244, а;
см.
также рис. 127). Изменяя перемещением
заслонки а
расстояние
х,
т.
е. изменяя проходное
сечение выходного регулируемого
дросселя, можем управлять давлением
р₁
в
проточной (междроссельной) камере и в
соединенном с ней пневмоцилиндре.
На рис. 244, 6
показана
экспериментальная кривая функ­ции
p₁
=
f
(x)
этой
системы.

При
малых давлениях питания (р₀
≤0,5 кГ/см²)
пневматическое
устрой­ство
этого типа можно приближенно рассчитывать
как гидравлическое, используя
уравнение постоянства расхода Q
через
оба дросселя.

В этом случае
имеем, согласно уравнению (19),

откуда
(полагая коэффициенты сопротивления
дросселей ζ₁
= ζ₂)

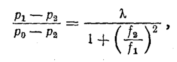
или

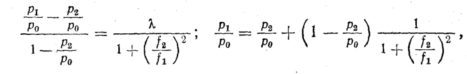
где

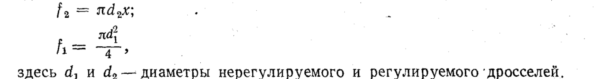
Электропневматическое
реле и индикатор давления. Для
контроля давле­ния
в пневмосистемах, осуществляемого
воздействием на контакты микро­переключателя,
включенного в электрическую цепь
управления, приме­няют
реле давления. Реле представляет собой
нагруженную пружиной мембрану
/, на которую действует рабочее давление
воздуха (рис. 245; см. также рис. 84, в).

Давление
воздуха, подводимого к каналу а,
действует
через мембрану 1
на
грибок 2
и
толкатель 5. Если усилие, развиваемое
давлением воздуха, превышает усилие
противодействующей пружины 3
(усилие
пружины регу­лируется винтом 4),
то
толкатель 5 перемещается и воздействует
на штифт микропереключателя 6.

Аналогичное
по принципу действия устройство,
называемое индикатором давления,
применяют для подачи сигнала о наличии
давления на определенных участках
пневмосистем. Этот индикатор представляет
собой миниатюр­ный
силовой пневмоцилиндр одностороннего
действия (рис. 246). В корпусе 1
цилиндра
перемещается поршенек 3,
уплотняемый
резиновой манжетой 4.
При
отсутствии давления на контролируемом
участке пневмосистемы поршенек
3
под
действием пружины 2 удерживается в
крайнем правом поло­жении. При появлении
же давления он, сжимая пружину 2,
перемещается влево. Выдвинутый шток 5
сигнализует
с помощью механических или элек­трических
устройств о наличии давления на том
участке пневмоцепи, к кото­рому
подключен индикатор давления.

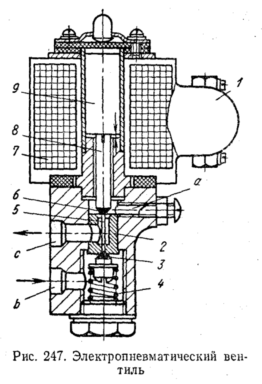
Электропневматический
вентиль. В
системах пневмоавтоматики приме­няются
для дистанционного управления воздушными
магистралями вентили (рис.
247), в которых проходные каналы закрываются
и открываются конусными клапанами,
управляемыми электромаг­нитом.
При
включении электротока, подводимого
через клеммную коробку /, якорь 9
перемещается
вниз и с помощью толкателя 8
и
клапана 6
перекры­вает
отверстие в верхнем седле клапана 2 и,
одновременно нажимая через толкатель
5
на
нижний клапан 3,
открывает
нижнее отверстие этого седла. При
этом сжатый воздух, поступающий из
магистрали в отверстие Ь,
направ­ляется
через отверстие с
к
потребителю.

При
обесточивании катушки 7 пружина 4
перемещает
вверх нижний кла­пан 3,
перекрывая
поступление воздуха из магистрали.
Одновременно с этим перемещается вверх
верхний клапан 6,
обеспечивая
сброс через канал в седле клапана 2
и
выпускное отверотие а
воздуха
из системы потребителя в атмо­сферу.

Гидропневматические
преобразователи давления. В
тех случаях, когда располагаемое
давление воздуха недостаточно для
получения при рацио­нальных
размерах пневмоагрегатов требуемых
усилий, применяют пневмо-гидравлические
преобразователи, в которых относительно
невысокое давле­ние
воздуха преобразовывается в высокое
давление жидкости, являющейся
рабочей
средой гидравлической части системы.
В частности, такие усили­тели применяют
в механизмах подачи металлообрабатывающих
станков, причем при применении их
представляется возможным получить
значи­тельные
усилия подачи при небольших давлениях
воздуха.

На
рис. 248, а
показана
схема распространенного пневмогидравлического
преобразователя
давления. Сжатый воздух под давлением
р_е
подается
в
левую полость а
цилиндра
преобразователя и, действуя на
дифференциаль­ный
поршень 1,
вытесняет
жидкость под повышенным давлением в
камеру Ь.
Это
давление действует на пор­шень
3,
развивая
усилие на што­ке 2.

Давление
жидкости в камере Ь

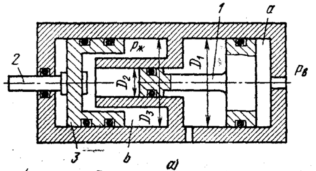
Усилие на штоке 2

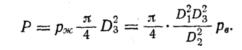
На
рис. 248, б
приведена
схема механизма
подачи сверлильного станка,
включающая преобразо­ватель
давления, пневмоцилиндр 4
большого
диаметра которого приводит
в движение два гидро­цилиндра
1
и 7 малого
диаметра, питающие
жидкостью исполни­тельный
силовой гидроцилиндр 3
механизма
подачи станка.

Давление
р₂
^в
полостях гидро­цилиндров
/ и 7 выше давления воздуха
р_ъ
подводимого
в пнев­моцилиндр
4.
Оно
пропорцио­нально отношению большой
F
и
малой f
площади
дифференциаль­ного
поршня:

Сжатый
воздух распределяется плоским золотником
9 с электромагнит­ным приводом. При
подаче воздуха в правую полость
пневмоцилиндра 4
поршень
его перемещается влево, в результате
поршень гидроцилиндра / преобразователя
подает жидкость в силовой гидроцилиндр
3
механизма
подачи станка.

Одновременно
жидкость из правой полости гидроцилиндра
3
вытесняется
через регулятор скорости, состоящий из
дросселя 6
и
обратного клапана 5, в правую полость
гидроцилиндра 7 преобразователя.

Регулятор
скорости имеет регулируемый дроссель
б,
обратный
клапан 5
и
обводный золотник (перепускной клапан)
8
с
электромагнитным управле­нием по
сигналам датчика 2.
В
начале хода поршня силового гидроцилин­дра
3
жидкость
вытесняется им через открытый в исходном
положении канал золотника 8
в
обход дросселя 6
и
после включения приводного электрома­гнита
золотника и перекрытия его плунжером
сливного канала — через дроссель 6.

Первая
часть хода является нерегулируемым
ускоренным подводом ин­струмента
к изделию и вторая — регулируемым
рабочим ходом.

При
обратном ходе поршня пневмоцилиндра 4
вправо
жидкость из гидро­цилиндра 7
преобразователя поступает через обратный
клапан 5
в
правую полость гидроцилиндра 3,
в
результате шпиндель станка ускоренно
пере­мещается
в исходное положение.