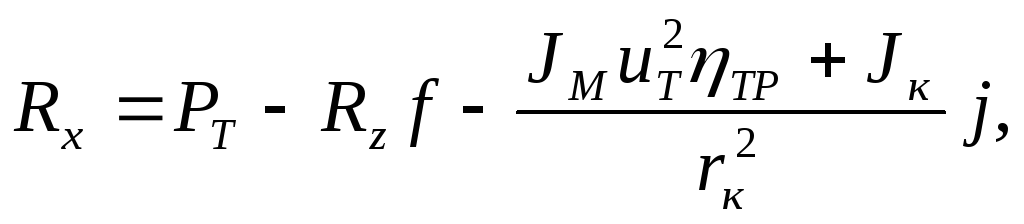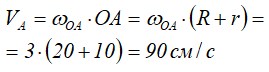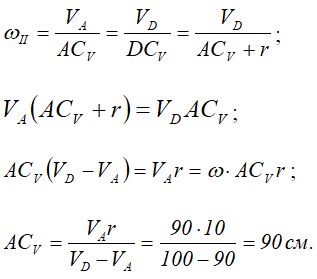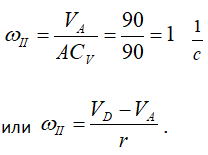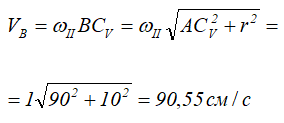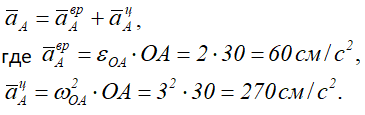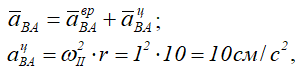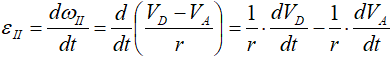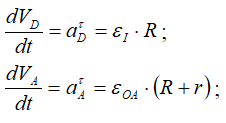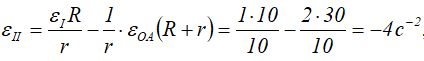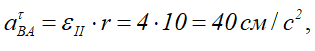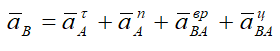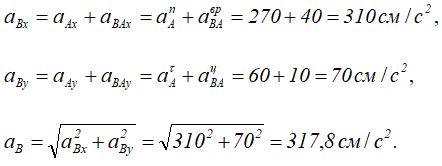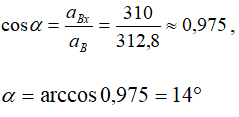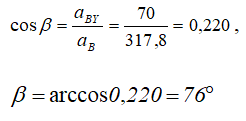Как найти скорость при движении колеса

Условие задачи:

Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает 309 оборотов в минуту.

Задача №1.8.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(D=1,1) м, (nu=309) об/мин, (upsilon-?)

Решение задачи:

Строго говоря, относительно Земли точки колеса при движении автомобиля совершают сложное движение, при котором они двигаются и поступательно, и вращательно. Но если перейти в систему отсчета (СО), связанную с автомобилем, то колеса будут уже совершать простое вращательное движение. При этом понятно, что линейная скорость крайних точек колеса равна скорости движения автомобиля (upsilon).

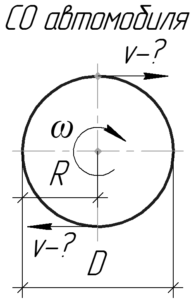
Эту линейную скорость можно определить по такой формуле, учитывая, что радиус равен одной второй диаметра:

[upsilon  = omega R = frac{{omega D}}{2};;;;(1)]

Угловую скорость (omega) найдем, используя частоту вращения (nu), данную в условии, по такому выражению:

[omega  = 2pi nu ;;;;(2)]

Подставим (2) в (1):

[upsilon  = frac{{2pi nu D}}{2} = pi nu D]

Перед тем, как подставлять значения и вычислять ответ, переведем частоту вращения в систему СИ.

[309; [1/мин] = frac{{309}}{{60}}; [1/с] = frac{{103}}{{20}}; [1/с]]

[upsilon  = 3,14 cdot frac{{103}}{{20}} cdot 1,1 = 17,79; м/с]

Ответ: 17,79 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.4 С какой скоростью едет велосипедист, если колесо делает 100 об/мин. Радиус
1.8.5 Угол поворота колеса радиусом 0,2 м изменяется по закону phi=9,42t (рад)

Линейную
скорость колеса, м/с, можно определить
с помощью
выражения

где
г_к
— радиус
колеса, м; ω
_к—
угловая
скорость колеса, рад/с.

Скорость
автомобиля при его прямолинейном
движении равна линейной
скорости колеса, т. е.

=

_к.

Так
как скорость автомобиля
обычно
выражается в км/ч,а
скорость колеса
_к
— в
м/с, то для получения скорости автомобиля

в
км/ч необходимо ввести переводной
коэффициент 3,6. С
учетом этого коэффициента скорость
автомобиля, км/ч:

Аналогично
при прямолинейном движении ускорение
автомобиля
равно линейному ускорению колеса:

(3.15)

3.7. Реакции дороги, действующие при движении на колеса автомобиля

При
движении автомобиля его колеса могут
катиться в различных
режимах: тяговом, ведомом и тормозном.
При этих режимах качения
со стороны дороги на колеса действуют
силы, называемые
реакциями. Для определения их величины
рассмотрим качение
колеса автомобиля по жесткой
(недеформируемой) дороге. Схема
сил, действующих в этом случае на ведущее
колесо, представлена
на рис. 3.5.

С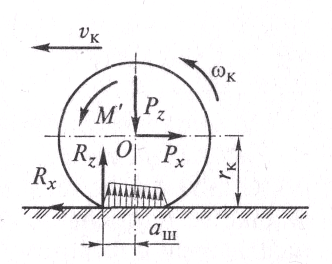илыР_х
и
Р_z.
и момент М’
действуют
на колесо со стороны автомобиля.
Силы R._x
и
R_z
действуют
на колесо со стороны дороги и
представляют собой ее реакции.

Рассмотрим указанные
силы и момент.

Рис.
3.5. Силы, действу­ющие
на ведущее колесо при
качении по недефор­мируемой
дороге: О
— центр
колеса

Р_z.
—
вертикальная нагрузка на колесо,
направленная вниз перпендикулярно
поверхности
дороги.

Р_х
—
продольная сила, параллельная поверхности
дороги. В зависимости от режима
качения колеса она может быть на­правлена
как в сторону движения автомобиля,
так и в противоположную.

M`—
момент,
подводимый к колесу от
полуоси или тормозного барабана
(тормозного
диска). Иногда момент может быть
равен нулю (не подводится к колeсу).
Момент считается положительным, если
его направление совпадает с направлением
вращения колеса, и наоборот.

R_z
— нормальная реакция дороги, направленная
вверх перпенди­кулярно
поверхности дороги. Точка приложения
нормальной реак­ции
смещена относительно оси колеса на
некоторую величину а_ш
из-за
большей деформации шины в набегающей
на дорогу части, чем
в сбегающей с дороги. Это подтверждает
эпюра элементарных сил,
действующих в месте контакта колеса с
дорогой, для кото­рых
нормальная реакция является результирующей
силой.

R_х
— касательная
реакция дороги. Это сила, которая
действует в плоскости
дороги и в зависимости от режима качения
колеса может быть направлена в сторону
движения автомобиля или в про­тивоположную.
Касательная реакция считается
положительной, если она направлена в
сторону движения, и наоборот.

Составим уравнение
моментов относительно оси колеса:

(3.16)

где
J_к
— момент инерции колеса относительно
оси вращения. Из выражения (3.16) находим
касательную реакцию дороги:

Обозначим
отношение

— символом ƒ и, выразив величину

с
помощью формулы (3.15) через ускорение
автомобиля j,для
касательной реакции дороги получим в
общем случае (при любых
режимах качения колеса)

(3.17)

Рассмотрим типичные
режимы качения колеса.

Тяговый
режим характерен
для ведущего колеса. Момент М’
подводится
к колесу через полуось, и направление
момента со­впадает с направлением
вращения колеса. В этом случае момент
называется крутящим. Подставляя в
выражение (3.17) вместо М’
выражение
для крутящего момента М_к,
подводимого
к ведущим колесам, и учитывая соотношения
(3.12) и (3.15), для ведущего колеса получим

Где


— тяговая
сила.

Для
ведущего колеса касательная реакция
R_х
> 0.
Следователь­но, она направлена в
сторону движения, как показано на рис.
3.5.

Ведомый
режим характерен
для ведомого колеса. Момент М’
к колесу
не подводится, и, следовательно, он равен
нулю. Для ведомого колеса касательная
реакция дороги

Знак
«-» показывает, что у ведомого колеса
касательная реакция дороги направлена
Тормозной
режим является
характерным для тормозящего колеса(ведущего,
ведомого). Момент М’
подводится
к колесу от тормозного барабана или
тормозного диска и направление его
противоположно направлению вращения
колеса. В этом случае момент называется
тормозным (М_тор).
Подставив
в выражение (3.17) вместо М’
тормозной
момент (М’
= -M_тор),
для тормозящего колеса получи против
движения (рис.3.6, а).

Рис.
3.6. Силы, действующие на ведомое (а
)и
тормозящее (б)
колеса

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Enter the rotations per minute (RPM) of the axle and the wheel diameter into the calculator to determine the wheel speed. This calculator can also evaluate the diameter or RPM when provided the other variables.

• Bike Speed Calculator
• Gear Inch Calculator
• Rev Per Mile Calculator
• Wheel Horsepower Calculator

Wheel Speed Formula

The following formula is used to calculate a wheel speed.

S = [2*PI*(D/2)] * [ RPM/60 ]

• Where S is the wheel speed
• RPM is the rotations per minute
• D is the diameter

To calculate wheel speed, multiply half the diameter by 2 times pi, then multiply again by the RPM over 60.

Wheel Speed Definition

What is wheel speed? Wheel speed commonly refers to the instantaneous tangential velocity of a wheel at a specific diameter that is rotating at a constant RPM.

Example Problem

FAQ

Does wheel size affect speed? Wheel size will change the speed of a vehicle if the RPM of the wheel stays constant. Increasing the wheel size will increase the speed when RPM is constant, and decreasing the wheel size will decrease the speed when RPM is constant. In the real world, keeping a constant RPM with a larger wheel requires more torque.

Расчет скорости колеса

Скорость колеса — это физическая величина, характеризующая скорость, с которой точка движется по окружности вокруг центра вращения.

Формула расчета скорости колеса:

V = 2 * π * R * n, где

V — линейная скорость;
R — радиус окружности;
n — угловая скорость.

Смотрите также перевод угловой скорости в линейную и наоборот — об/мин в м/с.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор для расчета скорости колеса по простой математической формуле в зависимости от скорости вращения и радиуса колеса. С помощью этой программы вы в один клик сможете рассчитать скорость колеса.

Угловая и линейная скорость

Переход от угловой к линейной скорости.

Сегодня смотрел на детей, катающихся на карусели, и подумал — а интересно, с какой скоростью они крутятся.
Подумав еще, понял, что ответить на этот вопрос очень просто, достаточно подсчитать, сколько оборотов в минуту они совершают.

Зная число оборотов в минуту, можно найти угловую скорость в радианах в секунду — за один оборот угол меняется на радиан, за минуту — радиан, и соответственно за секунду — радиан.

Это угловая скорость — радиан/сек. Переход к линейной тривиален — углу в 1 радиан соответствует дуга окружности равная радиусу, соответственно,

Вот и все, а ниже калькулятор. Скорость в м/с приводит к км/час, чтобы было понятнее.

Парадокс колеса

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w — угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.

Пример решения задачи по определению величины и направления полной скорости и полного ускорения при сложном движении точки колеса кривошипа.

Теория по теме

Задача

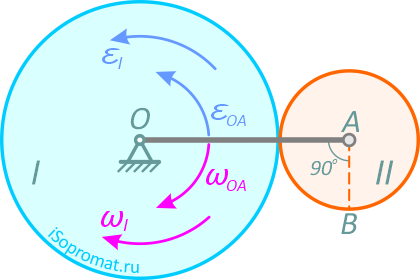
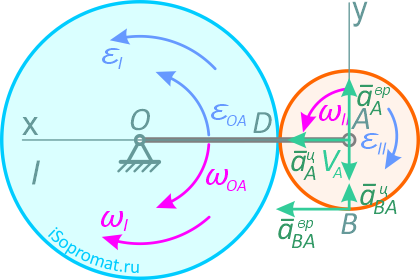
Колесо I с радиусом R вращается вокруг оси, проходящей через центр колеса перпендикулярно плоскости чертежа с угловой скоростью ω_I и угловым ускорением ε_I.

Рис. 2.7

Независимо от него на той же оси вращается кривошип ОА с угловой скоростью ω_OA и угловым ускорением ε_OA. Кривошип приводит в движение колесо II с радиусом r, которое катится по колесу I (рис. 2.7).

Найти скорость V_B и ускорение a_B точки B, если R=20 см, r=10 см, ω_I=5 с^-1, ε_I=1 с^-2, ω_OA=3 с^-1, ε_OA=2 с^-2.

Другие примеры решений >
Помощь с решением задач >

Решение

Колесо I и кривошип совершают вращательное движение, а колесо II – плоскопараллельное движение.

Найдем скорость точки В, для этого определим положение мгновенного центра скоростей колеса II. Чтобы найти МЦС нужно, знать направление скоростей хотя бы двух точек тела.

Найдем скорость точки А, которая принадлежит колесу II и кривошипу ОА.

Вектор V_A направлен перпендикулярно отрезку ОА в сторону вращения кривошипа (рис. 2.8).

Рис. 2.8

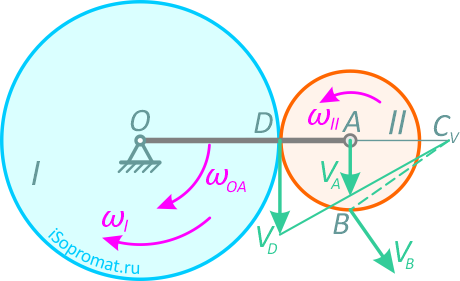
В точке соприкосновения колес скорость точки колеса II должна равняться скорости точки колеса I. Обозначим эту точку буквой D. Эта точка не принадлежит кривошипу ОА. Так как движение колеса I известно, можно найти скорость точки D.

Вектор скорости точки D направлен перпендикулярно радиусу OD в сторону вращения колеса I. Таким образом, нам известны скорости двух точек колеса II. Проведем перпендикуляр к скоростям в точках А и D и прямую, проходящую через концы векторов скоростей V_D и V_A.

В точке пересечения этих линий и будет МЦС для колеса II. Обозначим его буквой C_V.

Найдем расстояние AC_V:

Тогда

Зная угловую скорость колеса II и его МЦС, найдем скорость точки В.

Вектор V_B направлен перпендикулярно отрезку ВС_V в сторону вращения колеса II.

Определим ускорение точки В.

Согласно теореме, ускорение точки В определятся по формуле

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг
полюса А.

Точка А принадлежит кривошипу ОА – движение которого известно, тогда

Вектор a^τ_A — направлен перпендикулярно ОА, в сторону, обратную V_A, т.к. вращение кривошипа по условию задачи замедленное.

Рис. 2.9

Вектор aⁿ_A — направлен от А к О.

Вектор

и направлен от точки В к полюсу А.

Для его вычисления найдем угловое ускорение ε_II:

r – в задачах такого типа величина постоянная, выносится за знак производной:

Отсюда

Знак «-» говорит о том, что колесо II вращается замедленно.

Величина

и направлена перпендикулярно aⁿ_BA. Полное ускорение найдем, сложив все слагаемые:

Направив ось АX вдоль АО, ось АY перпендикулярно АО, получим:

Вектор a_B составляет с осью АХ угол α, косинус
которого

а с осью AY угол β, косинус которого:

Другие примеры решения задач >