Колебательное движение маятника
Образец решения
Вариант 3
1
Амплитуда колебания маятника:
2
Период колебания маятника:
3
Частота колебания: 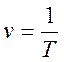
4
Длину маятника определяем из формулы: 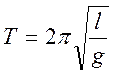
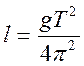
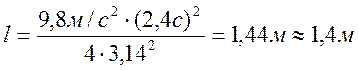
5
Смещение при фазе ;
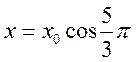
. Точка
М на графике соответствует фазе , а отрезок КМ-смещению
при этой фазе.
6
Циклическая (или круговая) частота равна 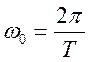
7
Наибольшее значение скорости вычисляем по
формуле: 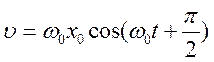
, равном
,
,
.
8
Кинетическая энергия при прохождении
маятником положения равновесия равна 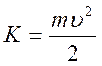
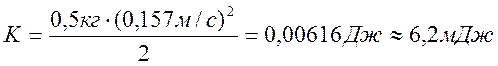
9
Скорость при фазе ,
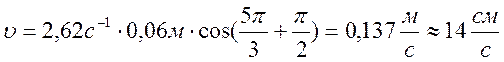
начертим график скорости. Отрезок, где BC показывает
величину скорости при фазе, (см. рисунок).
10 Ускорение при фазе ,
,
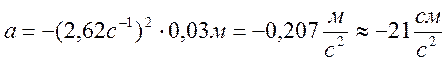
11 Сила при фазе ,
,
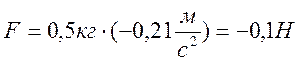
12 Энергия при фазе ;
а) кинетическая 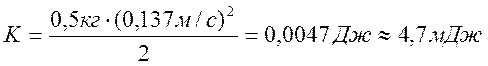
б) потенциальная .
13 Из формулы пружинного маятника 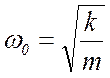
жесткость пружины ,
.
14 Удлинение пружины под действием груза 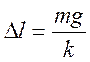
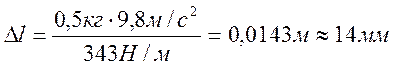
15 Электроемкость конденсатора определяем из формулы: ,
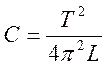
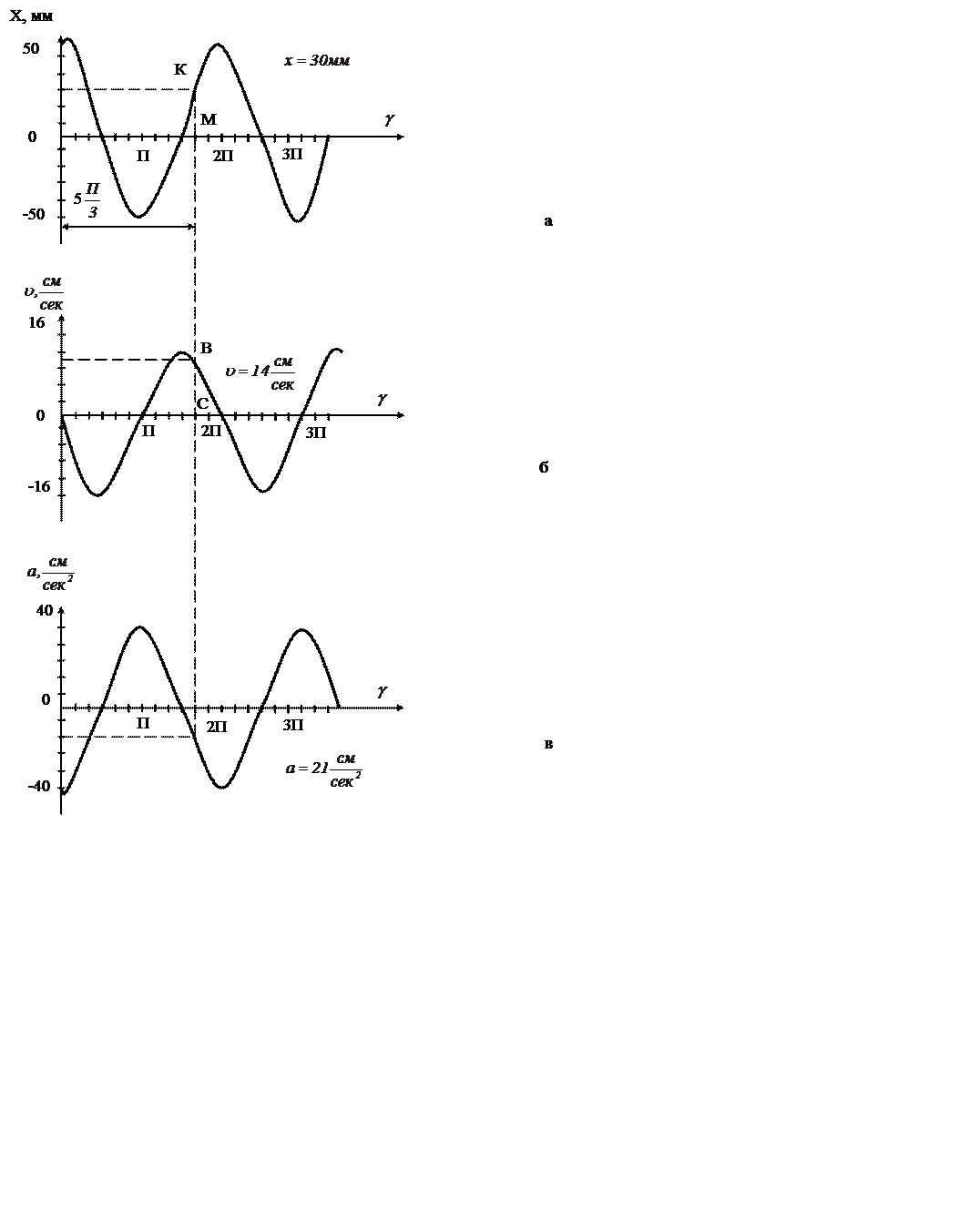
График напряжения переменного тока
На рисунке изображен график зависимости напряжения
переменного тока от времени. Используя график, выполните задания, ответьте на
вопросы.
1
Определите циклическую частоту тока.
2
Определите амплитудное значение
напряжения.
3
Вычислите действующее значение напряжения.
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ |
|
|
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
|
|
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
|
|
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. |
|
|
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
|
|
Скорость и ускорение при гармонических колебаниях. |
|
|
Согласно определению скорости, скорость – это производная от координаты по времени |
|
|
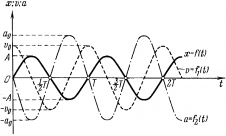
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
|
|
Величина |
|
|
Следовательно, для скорости при гармоническом колебании имеем: |
|
|
Согласно определению ускорения, ускорение – это производная от скорости по времени:
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). |
|
|
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: |
|
|
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). |
|
|
Сравним выражения для смещения и ускорения при гармонических колебаниях:
|
|
|
Можно записать: т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
|
|
Часто бывает удобно записывать уравнения для колебаний в виде: где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: |
|
Сила
Кориолиса равна:
,
где
—
точечнаямасса,—векторугловой
скоростивращающейся системы
отсчёта,—
вектор скорости движения точечной массы
в этой системе отсчёта, квадратными
скобками обозначена операциявекторного
произведения.
Величина
называется
кориолисовым ускорением.
24 вопрос
По физической природе
-
Механические(звук,вибрация)
-
Электромагнитные(свет,радиоволны,
тепловые) -
Смешанного типа— комбинации
вышеперечисленных
По характеру взаимодействия с окружающей средой
-
Вынужденные—
колебания, протекающие в системе под
влиянием внешнего периодического
воздействия. Примеры: листья на деревьях,
поднятие и опускание руки. При вынужденных
колебаниях может возникнуть явлениерезонанса:
резкое возрастание амплитуды колебаний
при совпадениисобственной
частотыосциллятораи частоты внешнего воздействия. -
Свободные (или собственные)—
это колебания в системе под действием
внутренних сил, после того как система
выведена из состояния равновесия (в
реальных условиях свободные колебания
всегдазатухающие).
Простейшими примерами свободных
колебаний являются колебания груза,
прикреплённого к пружине, или груза,
подвешенного на нити. -
Автоколебания—
колебания, при которых система имеет
запаспотенциальной
энергии, расходующейся на
совершение колебаний (пример такой
системы —механические
часы). Характерным отличием
автоколебаний от вынужденных колебаний
является то, что их амплитуда определяется
свойствами самой системы, а не начальными
условиями. -
Параметрические—
колебания, возникающие при изменении
какого-либо параметра колебательной
системы в результате внешнего воздействия. -
Случайные—
колебания, при которых внешняя или
параметрическая нагрузка является
случайным процессом.
Гармонические
колебания— колебания, при которых
физическая (или любая другая) величина
изменяется с течением времени по
синусоидальному или косинусоидальному
закону. Кинематическое уравнение
гармонических колебаний имеет вид
или
,
где
х— смещение (отклонение)
колеблющейся точки от положения
равновесия в момент времени t;А—
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия;ω— циклическая
частота, величина, показывающая число
полных колебаний происходящих в течение
2π секунд;—
полная фаза колебаний,—
начальная фаза колебаний.
Обобщенное
гармоническое колебание в дифференциальном
виде
(Любое
нетривиальное[1]решение этого дифференциального
уравнения — есть гармоническое
колебание с циклической частотой)
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость
– это производная от координаты по
времени
Таким образом, мы видим, что скорость
при гармоническом колебательном движении
также изменяется по гармоническому
закону, но колебания скорости опережают
колебания смещения по фазе на p/2.
Величина
— максимальная скорость колебательного
движения (амплитуда колебаний скорости).
Следовательно, для скорости при
гармоническом колебании имеем:
,
а для случая нулевой начальной фазы
(см. график).
Согласно определению ускорения, ускорение
– это производная от скорости по времени:
—
вторая производная от координаты по
времени. Тогда:

Ускорение при гармоническом колебательном
движении также изменяется по гармоническому
закону, но колебания ускорения опережают
колебания скорости на p/2
и колебания смещения наp(говорят, что колебания происходятв
противофазе).
Величина
— максимальное ускорение (амплитуда
колебаний ускорения). Следовательно,
для ускорения имеем:
,
а для случая нулевой начальной фазы:
(см. график).
Из анализа процесса колебательного
движения, графиков и соответствующих
математических выражений видно, что
при прохождении колеблющимся телом
положения равновесия (смещение равно
нулю) ускорение равно нулю, а скорость
тела максимальна (тело проходит положение
равновесия по инерции), а при достижении
амплитудного значения смещения –
скорость равна нулю, а ускорение
максимально по модулю (тело меняет
направление своего движения).
25 вопрос
Гармонические
колебания— колебания, при которых
физическая (или любая другая) величина
изменяется с течением времени по
синусоидальному или косинусоидальному
закону. Кинематическое уравнение
гармонических колебаний имеет вид
или
,
где
х— смещение (отклонение)
колеблющейся точки от положения
равновесия в момент времени t;А—
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия;ω— циклическая
частота, величина, показывающая число
полных колебаний происходящих в течение
2π секунд;—
полная фаза колебаний,—
начальная фаза колебаний.
Обобщенное
гармоническое колебание в дифференциальном
виде
(Любое
нетривиальное[1]решение этого дифференциального
уравнения — есть гармоническое
колебание с циклической частотой)
26 вопрос
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение гармонических колебаний
- Гармонические колебания как простейший периодический процесс
- Перемещение, скорость и ускорение при гармоническом движении
- Примеры
п.1. Гармонические колебания как простейший периодический процесс
Процессы, в которых состояние системы полностью повторяется через определенные промежутки времени, называются периодическими.
Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.
Минимальное время T, в течение которого система возвращается в исходное состояние, называется периодом.
Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10-14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·1015 с
Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sint) и (cost) с периодом (T=2pi).
Простейшим периодическим процессом являются гармонические колебания, для которых состояние системы изменяется со временем по закону синуса или косинуса: $$ x(t)=Asin(omega t+varphi_0) text{или} x(t)=A cos(omega t+varphi_0) $$ где:
(x(t)) – отклонение характеристики системы от среднего за период значения;
(A) – амплитуда колебаний, максимальное отклонение от среднего за период значения;
(omega) – циклическая частота, изменение фазы колебаний за 1 с, рад/с;
(varphi_0) – начальная фаза колебаний, значение фазы при t=0, рад;
((omega t+varphi_0) )– полная фаза колебаний (просто «фаза»), рад;
Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:
Период гармонических колебаний равен: $$ T=frac{2pi}{omega} $$
Число колебаний в единицу времени называют частотой. Частота является величиной, обратной периоду: $$ nu=frac1T $$ Связь циклической частоты и частоты: (omega=2pinu)
Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin{gather*} nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac{20}{10}=4pi text{(рад/с)} end{gather*} Получаем закон колебаний: (x(t)=5cos(4pi t))
п.2. Перемещение, скорость и ускорение при гармоническом движении
Пусть (x(t)) — координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acosomega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-Aomega sinomega t=Aomega cosleft(omega t+fracpi 2right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $$ v_m=Aomega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x»(t)=-Aomega^2 cosomega t=Aomega^2 cos(omega t+pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $$ a_m=Aomega^2 $$ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:
Из уравнения для ускорения получаем: $$ x»(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $$ Откуда следует:
Уравнение гармонических колебаний: $$ x»(t)+omega^2x(t)=0 $$
Решением этого уравнения в общем виде будут: $$ x(t)=Asin(omega t+varphi_0) text{или} x(t)=A cos(omega t+varphi_0) $$ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.
п.3. Примеры
Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?
 |
Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения. |
По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin{gather*} F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end{gather*} Уравнение движения грузика: $$ x»(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt{frac km})
Общее решение уравнения: (x(t)=Acosleft(sqrt{frac km}+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt{frac km}, a_m=Afrac km $$ Ответ: (omega=sqrt{frac km})
Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?
 |
Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g. |
В положении равновесия на шарик действуют и уравновешивают друг друга две силы: сила тяжести mg и сила натяжения нити FH.
В положении максимального отклонения под углом α к вертикали равнодействующая уже не равна 0, и, как только мы отпустим шарик, он начинает перемещаться вниз. Уравнение движения: begin{gather*} moverrightarrow{a}=-overrightarrow{F_H}-moverrightarrow{g} end{gather*} (overrightarrow{F_H}perpoverrightarrow{F}) т.к. равнодействующая (overrightarrow{F}=moverrightarrow{a}) направлена по касательной. В проекции на направление (overrightarrow{F}) сила натяжения (overrightarrow{F_H}) даст 0, а сила тяжести (mgsinalpha). Получаем: begin{gather*} ma=0-mgsinalpha=-mgsinalpha\ a=-gsinalpha end{gather*} Для смещения x по дуге окружности радиусом угол (alpha=frac xl). Для небольших углов (до 20°) (sinfrac xlapproxfrac xl) (см. приближения функций при малых x в §52 данного справочника). Поэтому: $$ a=-gsinfrac xlapprox-frac gl x $$ И мы получаем уравнение гармонических колебаний: (x»(t)+frac gl x=0, omega=sqrt{frac gl})
Общее решение уравнения: (x(t)=Acosleft(frac gl t+varphi_0right))
Амплитудные значения скорости и ускорения: (v_m=Asqrt{frac gl}, a_m=Afrac gl)
Ответ: (omega=sqrt{frac gl})
Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?
 |
LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем. |
Напряжение на конденсаторе (U_C(t)=frac{Q(t)}{C}). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac{triangle I}{triangle t}). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin{gather*} U_c(t)=varepsilon_L(t)Rightarrow frac{Q(t)}{C}=-LI'(t)Rightarrow frac{Q(t)}{C}+LI'(t)=0 end{gather*} Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin{gather*} frac{Q(t)}{C}+LQ»(t)=0 end{gather*} Получаем уравнение гармонических колебаний: $$ Q»(t)=frac{1}{LC}Q(t)=0, omega=frac{1}{sqrt{LC}} $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac{1}{sqrt{LC}}t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac{Q(t)}{C}=frac{Q_m}{C}cosleft(frac{1}{sqrt{Lc}}t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac{Q_m}{C})
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac{Q_m}{sqrt{LC}}sinleft(frac{1}{sqrt{LC}}t+varphi_0right)=frac{Q_m}{sqrt{LC}}cosleft(frac{1}{sqrt{LC}}t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac{Q_m}{sqrt{LC}})
Ток опережает колебания заряда и напряжения на (fracpi 2)
Ответ: (omega=frac{1}{sqrt{LC}})
From Wikipedia, the free encyclopedia
Frequency dispersion in groups of gravity waves on the surface of deep water. The ■ red square moves with the phase velocity, and the ● green circles propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The red square overtakes two green circles when moving from the left to the right of the figure.
New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.
For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.
Propagation of a wave packet demonstrating a phase velocity greater than the group velocity without dispersion.
This shows a wave with the group velocity and phase velocity going in different directions. The group velocity is positive, while the phase velocity is negative.[1]
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as
Equivalently, in terms of the wave’s angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represent the angular change per unit of space,
To gain some basic intuition for this equation, we consider a propagating (cosine) wave A cos(kx − ωt). We want to see how fast a particular phase of the wave travels. For example, we can choose kx — ωt = 0, the phase of the first crest. This implies kx = ωt, and so v = x / t = ω / k.
Formally, we let the phase φ = kx — ωt and see immediately that ω = -dφ / dt and k = dφ / dx. So, it immediately follows that
As a result we observe a inverse relation between the angular frequency and wavevector. If the wave has higher frequency oscillations, the wave length must be shortened for the phase velocity to remain constant.[2] Additionally, the phase velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed the speed of light in vacuum, but this does not indicate any superluminal information or energy transfer.[citation needed] It was theoretically described by physicists such as Arnold Sommerfeld and Léon Brillouin.
The previous definition of phase velocity has been demonstrated for an isolated wave. However, such a definition can be extended to a beat of waves, or to a signal composed of multiple waves. For this it is necessary to mathematically write the beat or signal as a low frequency envelope multiplying a carrier. Thus the phase velocity of the carrier determines the phase velocity of the wave set.[3]
Group velocity[edit]
A superposition of 1D plane waves (blue) each traveling at a different phase velocity (traced by blue dots) results in a Gaussian wave packet (red) that propagates at the group velocity (traced by the red line).
The group velocity of a collection of waves is defined as
When multiple sinusoidal waves are propagating together, the resultant superposition of the waves can result in an «envelope» wave as well as a «carrier» wave that lies inside the envelope. This commonly appears in wireless communication when modulation (a change in amplitude and/or phase) is employed to send data. To gain some intuition for this definition, we consider a superposition of (cosine) waves f(x, t) with their respective angular frequencies and wavevectors.
So, we have a product of two waves: an envelope wave formed by f1 and a carrier wave formed by f2 . We call the velocity of the envelope wave the group velocity. We see that the phase velocity of f1 is
In the continuous differential case, this becomes the definition of the group velocity.
Refractive index[edit]
In the context of electromagnetics and optics, the frequency is some function ω(k) of the wave number, so in general, the phase velocity and the group velocity depend on specific medium and frequency. The ratio between the speed of light c and the phase velocity vp is known as the refractive index, n = c / vp = ck / ω.
In this way, we can obtain another form for group velocity for electromagnetics. Writing n = n(ω), a quick way to derive this form is to observe
We can then rearrange the above to obtain
From this formula, we see that the group velocity is equal to the phase velocity only when the refractive index is a constant dn / dk = 0. When this occurs, the medium is called non-dispersive, as opposed to dispersive, where various properties of the medium depend on the frequency ω. The relation ω = ω(k) is known as the dispersion relation of the medium.
See also[edit]
- Cherenkov radiation
- Dispersion (optics)
- Group velocity
- Propagation delay
- Shear wave splitting
- Wave propagation
- Wave propagation speed
- Planck constant
- Speed of light
- Matter wave#Phase velocity
References[edit]
Footnotes[edit]
- ^ Nemirovsky, Jonathan; Rechtsman, Mikael C; Segev, Mordechai (9 April 2012). «Negative radiation pressure and negative effective refractive index via dielectric birefringence». Optics Express. 20 (8): 8907–8914. Bibcode:2012OExpr..20.8907N. doi:10.1364/OE.20.008907. PMID 22513601.
- ^ «Phase, Group, and Signal Velocity». Mathpages.com. Retrieved 2011-07-24.
- ^ «Phase Velocity: Waves and Signals». electroagenda.com.
Bibliography[edit]
- Crawford jr., Frank S. (1968). Waves (Berkeley Physics Course, Vol. 3), McGraw-Hill, ISBN 978-0070048607 Free online version
- Brillouin, Léon (1960), Wave Propagation And Group Velocity, New York and London: Academic Press Inc., ISBN 978-0-12-134968-4
- Main, Iain G. (1988), Vibrations and Waves in Physics (2nd ed.), New York: Cambridge University Press, pp. 214–216, ISBN 978-0-521-27846-1
- Tipler, Paul A.; Llewellyn, Ralph A. (2003), Modern Physics (4th ed.), New York: W. H. Freeman and Company, pp. 222–223, ISBN 978-0-7167-4345-3

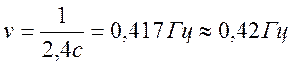
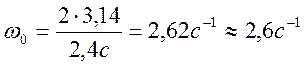
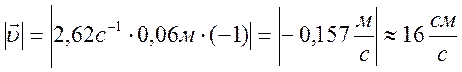
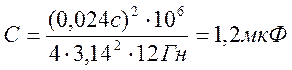
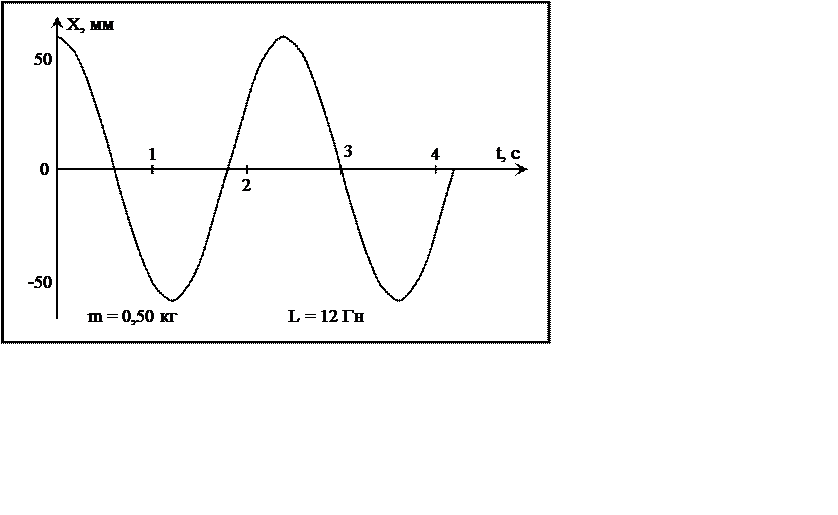
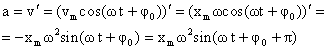 .
.










