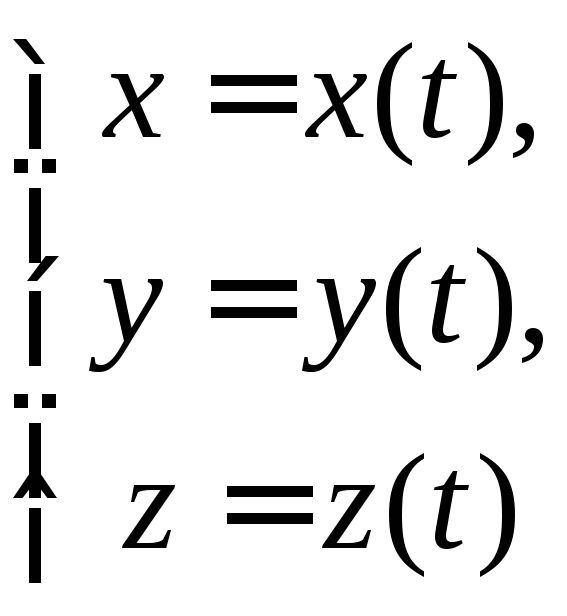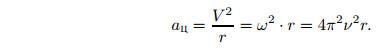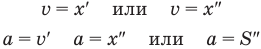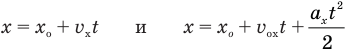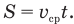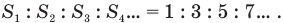-
Движение с переменным ускорением Рассматривая формулу определения ускорения в общем случае
как
дифференциальное уравнение с разделяющимися
переменными, скорость тела можно найти
после интегрирования:

Аналогично, рассматривая формулу определения скорости в общем случае
как
дифференциальное уравнение с разделяющимися
переменными, положение тела в пространстве
можно найти после интегрирования:
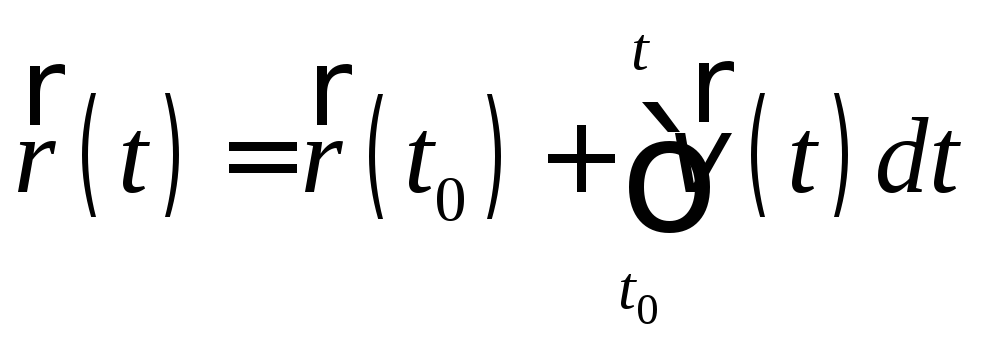
Путь,
пройденный телом за промежуток времени
(Δt
= t
– t0),
можно вычислить как интеграл от модуля
скорости:

Радиус-вектор,
как и любой другой вектор, можно выразить
через проекции и орты выбранной системы
координат. Формула
;
представляет
радиус-вектор в декартовой системе
координат.
Система
функций
является уравнением
траектории в параметрической форме,
где параметром является времяt.
Если движение происходит в одной
плоскости, напримерxOy,
то можно получить уравнение траектории
в явном виде:,
для чего нужно из первых двух функций
системы исключить время.
Вопросы
для самопроверки и задачи
1)
Выведите формулы зависимости скорости
и перемещения от времени, если известна
зависимость ускорения от времени.
2)
Выведите уравнение траектории движения
тела, брошенного под углом к горизонту.
3)
Запишите радиус-вектор в виде разложения
по базису декартовой системы координат.
4)
Выведите формулы для нахождения скорости
и ускорения тела в декартовой системе
координат.
-
Обратная
задача механики
Задача
45.
(1, 2) Найти размерность постоянных А,
В
и С;
радиус-вектор в момент времени, равный
2,6 с, и изобразить его на рисунке;
перемещение за промежуток времени от
t1
= 0,73 с до t2
= 2,3 с; его модуль; написать уравнение
траектории, если частица движется таким
образом, что ее радиус-вектор меняется
с течением времени по закону:
а); б)
;
в)
; г)
;
д)
; е)
,
где
А
= 1,8; В
= 4,3; С
= 1,7 – постоянные коэффициенты.
Задача
46.
(2) Реактивный снаряд
движется в плоскости yOz
так, что его координаты меняются с
течением времени по закону:
м;
м. Найти уравнение траектории и
тангенциальное ускорение снарядав момент времени, равный 86 с.
Задача
47.
(2) Движение бегуна на стадионе задано
формулами:
;
,
гдеα
= 4,3 м; β
= 2,4 м/с2;
γ
= 3,1 м; σ
= 5,2 м/с. Найти:
1)
скорость спортсмена в тот момент, когда
его координата х
равна 4,7 м; 2)
зависимость ускорения спортсмена от
времени.
Задача
48.
(3) Голубь перемещается в пространстве
так, что его радиус-вектор
меняется с течением времени по закону:
,
где
А
= 0,53 м/с2;
В
= 0,32 м/с2;
С
= 2,8 м. Найти: 1) путь, который пролетела
птица за 16 с от начала полета; 2) модуль
мгновенного ускорения в момент времени,
равный 0,85 с.
Задача
49.
(3) Зависимость
координат модели гоночного автомобиля
от
времени имеет вид:
,
гдеА
= 5,6 м;
ω
=
2,1 рад/с. Определить зависимость модуля
нормального и тангенциального
ускорения от времени, а также путь,
пройденный моделью за 73 с.
Задача
50.
(3) Снаряды вылетают с начальной скоростью
550 м/с под углом 30, 45 и 60о
к горизонту. Определить радиус кривизны
траектории снарядов в их наивысшей и
начальной точках.
Задача
51.
(3) С вышки высотой 14,7 м в горизонтальном
направлении брошен камень с начальной
скоростью 12
.
Определить скорость, тангенциальное и
нормальное ускорение камня спустя 0,83
с после начала его движения. Чему равны
радиус кривизны и расстояние до земли
в этой точке траектории? Сопротивлением
воздуха пренебречь.
-
Прямая
задача механики
Задача
52.
(2, 3) Найти размерность постоянных А,
В,
С,
D
и зависимость вектора перемещения
материальной точки от времени, если
материальная точка движется таким
образом, что вектор ее скорости меняется
с течением времени по закону:
а)
; б)
;
в)
; г)
;
д)
; е)
.
Задача
53.
(3) Частица движется с зависящим от
времени ускорением:
,где
А
= 2,4 м/с3;
В
= 7,1 м/с2.
Найти в момент времени, равный 2,7 с модуль
скорости, модуль радиуса-вектора, а
также путь и перемещение частицы за
промежуток времени от t1
= 1,4 с до t2
= 3,8 с. В начальный момент времени частица
покоилась в начале координат.
Задача
54.
(2) Скорость стартующего на вираже
автомобиля меняется с течением времени
по закону:
,
гдеА
= 2,4 м/с4;
В
= 1,6 м/с3.
Найти:
1) модуль приращения ускорения за время
от t1
= 1,3 с до t2
= 3,2 с;
2)
приращение радиуса-вектора за это время.
В начальный момент времени автомобиль
находился в начале координат.
Задача
55.
(2) Скорость зайца меняется с течением
времени по закону:
,
где α = 2,4 м/с2;
β = 5,3 м/с; γ = 3,7 м/с3.
Вычислить скорость зайца в момент
времени, равный нулю, найти зависимость
ускорения и радиуса-вектора зайца от
времени.
Задача
56.
(3) Ускорение взлетающего вертолета
меняется по закону:
,
гдеА
= 3,2 м/с3;
В
= 4,8 м/с5/2.
Вычислить: 1) модуль вектора скорости в
момент времени, равный 2,3 с; 2) приращение
радиуса-вектора за промежуток времени
от t1
= 1,2 с до t2
= 3,6 с. В начальный момент времени вертолет
покоился в начале координат.
Задача
57.
(2) Шарик, запрессованный в обод маховика,
движется по окружности радиусом 23 см
так, что зависимость пути от времени
описывается уравнением: l
= A + Ct3,
где С
= 0,52 м/с3.
Найти момент времени, когда угол между
тангенциальным и полным ускорением
шарика будет равен 30о.
Задача
58.
(3) Гайка на ободе центрифуги движется
по окружности радиусом R.
Модуль скорости гайки зависит от
пройденного пути по закону:
,
гдеВ
– постоянная. Найти угол между вектором
полного ускорения и вектором скорости
в зависимости от l.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скорость, ускорение, равномерное и равноускоренное прямолинейное движение
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
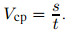
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
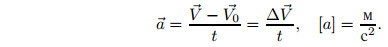
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt, где x0 — начальная координата тела, Vx — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с 2 , не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле: 
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости ω:
Угловая скорость связана с линейной скоростью соотношением 
где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).
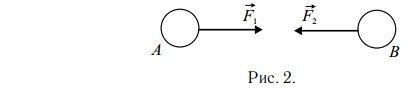
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле 
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести — это сила, с которой все тела притягиваются к Земле: 
При неподвижной опоре вес тела равен по модулю силе тяжести: 
Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес 
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес 
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите. 
где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3). 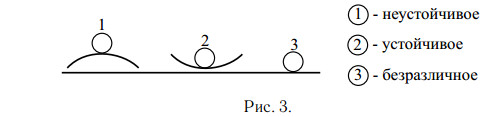
Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю. 
Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей 
где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае 
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом: 
где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения
Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность — это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле 
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле 
где h — высота подъёма
Энергия сжатой пружины: 
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волны
Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени: 
Частота измеряется в с -1 . Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле 
где l — длина маятника.
Период колебаний груза на пружине определяется по формуле 
где k — жёсткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе: 
где v — скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
Движение с переменным ускорением
Движение с переменным ускорением
Здесь 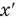
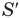
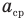
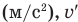
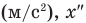
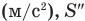
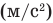
Правило сложения классических скоростей:
Здесь 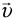
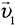
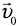
Если из условия задачи следует, что тело начало движение из состояния покоя, например, поезд отошел от станции или автомобиль выехал из пункта А и т. п., то в «Дано:» следует записать, что его начальная скорость 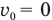
Из сравнения уравнений
следует, что если координата тела х зависит от времени движения t в первой степени, то это равномерное движение, а если координата х зависит от времени 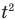
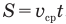
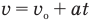
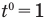
Если вам дано уравнение типа 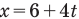
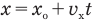
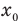
Если вам дано уравнение типа 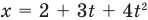
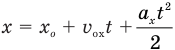
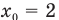
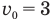
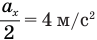
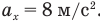
Формулу средней скорости 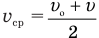
Пути, проходимые телом при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел:
Если в условии задачи идет речь о скорости в средней точке пути, то учтите, что это не средняя скорость на всем пути, а мгновенная скорость на середине пути, — она является конечной скоростью для первой половины пути и начальной скоростью для второй половины.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
http://lfirmal.com/dvizhenie-s-peremennyim-uskoreniem-v-fizike/
Движение с переменным ускорением
Здесь 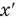
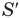
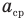
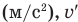
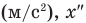
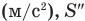
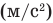
Правило сложения классических скоростей:
Здесь 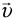
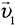
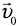
Если из условия задачи следует, что тело начало движение из состояния покоя, например, поезд отошел от станции или автомобиль выехал из пункта А и т. п., то в «Дано:» следует записать, что его начальная скорость 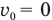
Из сравнения уравнений
следует, что если координата тела х зависит от времени движения t в первой степени, то это равномерное движение, а если координата х зависит от времени 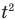
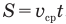
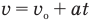
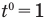
Если вам дано уравнение типа 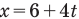
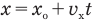
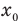
Если вам дано уравнение типа 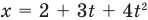
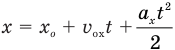
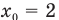
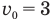
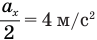
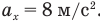
Формулу средней скорости 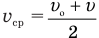
Пути, проходимые телом при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел:
Если в условии задачи идет речь о скорости в средней точке пути, то учтите, что это не средняя скорость на всем пути, а мгновенная скорость на середине пути, — она является конечной скоростью для первой половины пути и начальной скоростью для второй половины.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
В этой статье мы увидим, как найти скорость с ускорением, а также на некоторых примерах и решим некоторые проблемы.
Ускорение объекта прямо пропорционально изменению скорости со временем. Для объекта, ускоряющегося по круговому или параболическому пути, скорость остается касательной к дуге.
Как определить скорость по угловому ускорению?
Угловое ускорение определяется как изменение угловой скорости относительно изменения продолжительности времени и представлено как
а=Δω/Δt—(1)
Угловая скорость может быть определена путем вычисления изменения угла θ во времени. Следовательно,
так как ω = d/dt — (2)
Следовательно, мы можем записать предыдущее уравнение как
поэтому а=d2θ/дт2
Из уравнения (1),
dω = adt
Интегрируя уравнение
∫ dω =∫ adt
ω = at+C—(3)
Когда t=0, ω=ω0
И, следовательно, C=ω0
Подставляя это в уравнение (3)
ю = ю0+в -(4)
Это показывает, что угловая скорость объекта при круговом движении равна его начальной угловой скорости и ускорению объекта во времени.
Рассмотрим частицу, движущуюся по окружности с угловой скоростью ω
Пусть s — расстояние, пройденное частицей за время t. Если радиус кругового пути равен ‘r’, тогда ‘θ’ будет углом, образованным частицей, перемещающейся на расстояние ‘s’.
Тогда линейная скорость частицы будет равна перемещению частицы за время t. Смещение здесь — s. Следовательно, скорость задается как
v=Δs/Δt—(5)
Изменение угла θ при смещении частицы равно отношению длины дуги к радиусу окружности.
Δθ = с/р
поэтому s=Δθr
Подставляя это в уравнение (5)
v=r Δθ/Δt
Поскольку угловая скорость равна изменению угла во времени; мы можем переписать уравнение в виде
v=rω—(6)
Где ω — угловая скорость
Это подразумевает, что линейная скорость частицы является произведением радиуса кругового пути, пройденного частицей, и угловой скорости.
Problem1: Человек, стоящий в гравитроне диаметром 6 м, ускоряется со скоростью 15 м / с. Какой должна быть линейная скорость гравитрона. Начальная скорость гравитрона 4 м / с. Какое ускорение гравитрона за время 3 мин?
Дано: Радиус r = 3м
Начальная угловая скорость ω0= 4 м / с
Конечная угловая скорость ω=15м/с
Линейная скорость гравитрона при достижении угловой скорости 15 м / с.
v = rω
v=3*15=45м/с
Ускорение гравитрона за время 3 мин.
ω=ω0+ в
15=4+а*3
11=а*3
а=11/3
а = 3.67 м / с2
Следовательно, ускорение в момент времени t = 3 мин составляет 3.67 м / с.
Problem2: Автомобиль, разгоняющийся по круговой дорожке, набирает начальную скорость 20 км/ч и разгоняется до скорости 15 км/ч^2. Какова скорость автомобиля через 15 минут?
Дано: ω0=20 км/ч
а = 15 км / ч2
t=15 минут=15/60=0.25 часа
Следовательно,
ю = ю0+ в
ш =20+15*0.25
ω =20+3.75=23.75 км/ч
Следовательно, скорость автомобиля через 15 минут будет 23.75 км / ч.
Связь между скоростью, смещением и ускорением
Мы вывели уравнение для расчета конечной скорости на основе ускорения и зная начальную скорость системы.
Рассматривая то же уравнение (4) из приведенного выше, мы можем записать
v = v0+ в
Где v — конечная скорость
v0 начальная скорость
А — ускорение частицы.
Скорость определяется как изменение положения объекта между временным интервалом.
дх/дт=в0+ в
дх=(v0+в)дт
Интегрируя приведенное выше уравнение
∫dx=∫(v0+в)дт
]х=v0t+1/2 в2 -(Один)
Поскольку скорость определяется перемещением в единицу времени, перемещение равно произведению средней скорости и времени.
х=v→т — (8)
Где v→ средняя скорость, равная v→=v0т+в/2
Из уравнения (4) получаем t=vv0/a
Подставляя это в приведенное выше уравнение (), мы имеем
х=v+v0/2*вв0/a
х=v2 -v02/2а —(9)
Преобразуя это уравнение
v2=v02+2 топор—(10)
Это еще одно кинематическое уравнение для частицы в прямолинейное движение.
Как определить скорость по центростремительному ускорению?
Скорость объекта, ускоряющегося по круговой траектории, перпендикулярна направлению центростремительной силы, действующей внутрь.
Центростремительная сила и скорость движущегося объекта задаются соотношением
Fc=мв2/ г—(11)
Где r — радиус круга
V — линейная скорость
M — масса частицы
Объект массы m, ускоряющийся по круговой траектории радиуса r, линейная скорость равна радиусу круговой траектории и угловой скорости частицы.
v = rω
Где ω угловая скорость частицы
И сила равна произведению массы на ускорение объекта.
Подставляя это в уравнение (7);
F=мистер2ω2/r
F=мрω2
ма=мрω2
а=rω2 -(Один)
Следовательно, ускорение и скорость частицы при центростремительном движении связаны уравнением (8), согласно которому Ускорение движущейся частицы является произведением радиуса круговой траектории и квадрата угловой скорости, достигнутой частицей..
Problem3: Мальчик привязал камень к одному концу веревки длиной 1 м, а другой конец веревки держит в руке и вращает круговыми движениями со скоростью 2 оборота в секунду. Рассчитать угловую скорость камня?
Решение: Поскольку длина каната составляет 1 м, радиус круговой траектории равен 1 м.
За 1 секунду камень совершает 2 оборота, которые равны двум окружностям кругового пути, пройденного камнем.
Окружность кругового пути
С=2π г=2π* 1=2π
Следовательно, камни преодолевают расстояние 2 * 2π = 4π за одну секунду.
Следовательно, угловое ускорение камня равно
а =4π/с
Следовательно, угловая скорость камня равна
поэтому а=rω2
4π =1*ω2
ω =√4π =0.6 м/с
Problem4: Шар радиуса 0.3 м движется со скоростью 5 м / с по окружности диаметром 5 м. Какая угловая скорость мяча?
Дано: r = 5m
V = 5m / с
Используя уравнение v=ωr
Угловая скорость мяча равна
ω = v / r
ω=5/5=1 об/с
Подробнее о центростремительное ускорение.
Как определить скорость по переменному ускорению?
Считается, что объект движется с переменным ускорением, если его скорость часто меняется в разные промежутки времени.
Если ускорение частицы равно а, то а=dv/dt, которое меняется со временем t. Скорость можно вычислить, интегрируя уравнение dv=adt.
Рассмотрим частицу ускорение со скоростью v1 в случайном движении. Если частица вдруг изменит свое направление и скорость от v1 к V2 после временного интервала t1 к т2.Тогда ускорение a1 частицы
a1=v2-v1/t2-t1
Если в момент t1= 0, v1= 0, а при t2= 30 секунд, v2= 3 м / с, то
a1=3-0/30-0=3/30=0.1m/s2
Опять же, частица меняет направление и достигает скорости v3 в момент t3.
Теперь ускорение из-за изменения скорости частицы становится
a1=v3-v3/t3-t3
Если в t3= 60 секунд v3 = 8 м / с,
a1=8-3/60-30=5/30=0.167m/s2
Следовательно, изменение ускорения теперь из-за случайного движения частицы равно
Δа=а2-a1=0.167-0.1=0.067 м/с2
Что составляет примерно 0.07 м/с.2
Problem5: Если ускорение частицы задается уравнением a=6t2+4t, найти скорость частицы в момент времени t=2 с.
Решение: а=6t2+ 4т
дв/дт=6t2+ 4т
дв=(6t2+4т)дт—————(13)
Вышеупомянутое уравнение является переменным со временем t, поэтому оно называется переменным ускорением, потому что время не является постоянным.
Интегрирующее уравнение (13)
∫dv=∫6t2+4дт
v=6t3/3+4т2/2
v=2t3+ 2т2
v=2(т3+t2)
Когда время t = 2 секунды
v=2(23+22)
v = 2 (8 + 4)
v=2*12=24 м/с
Следовательно, скорость частицы составляет 24 м / с.
Как найти скорость с помощью ускорения и радиуса?
Когда объект ускоряется по кругу, он создает центростремительную силу, направленную к центру круга.
Если r — радиус круга, а m — масса объекта, то центростремительная сила, действующая на объект, определяется выражением
Fc=мв2/r
Так как Фc=ма
ма=мв2/r
а=в2/ г—(14)
v=√ar—(15)
Следовательно, скорость прямо пропорциональна квадратному корню из произведения ускорения и радиуса круга.
Как найти скорость с помощью ускорения и угла?
Ускорение определяется как отношение изменения угловой скорости во времени.
Для объекта, движущегося по круговой траектории, скорость и, следовательно, ускорение объекта измеряются в единицах изменения угла θ.
а=dω/dθ
Используя приведенное выше уравнение (4)
ю = ю0+ в
Так как ω = dθ /dt
Следовательно,
dθ/dt=ω0+ в
dθ=(ω0+ат) дт
Интегрируя это уравнение
∫dθ=∫(ω0+ат) дт
θ=ω0+1/2 в2
ω0=θ т-1-1/2 в -(16)
Вышеприведенное уравнение показывает связь между скоростью omega _0, ускорением «а» и углом θ.
Problem6: Угловая скорость двигателя увеличивается с 1800 об/мин до 2400 об/мин за 10 секунд. Найти угловое ускорение и количество оборотов мотора за это время?
Начальная угловая скорость в рад / сек.
ω0=2π*1800
=2π*1800/60=60π рад/с
Конечная угловая скорость в рад / сек.
ω =2π*2400
=2π*2400/60=80πрад/с
Угловое ускорение a=ω-ω0/t
a=(80-60)π/10=2π рад/с2
Угловое ускорение двигателя 2π рад/с.2
Угловое смещение во времени t определяется выражением
θ=ω0t+1/2 в2
=60π*10+1/2 * 2 Пи π *102
=600π +100π=700π
Число оборотов = 700π/2π=350
Следовательно, двигатель делает 350 оборотов в секунду.
Как найти скорость с помощью ускорения и силы?
Нормальная сила определяется как произведение массы и ускорения, тогда как сила, приложенная к объекту, равна отношению проделанной работы и смещения объекта.
При центростремительном движении сила пропорциональна квадрату скорости объекта, отслеживающего круговой путь, и массе объекта и обратно пропорциональна удалению объекта от центра кругового пути.
При прямолинейном движении конечная скорость объекта связана с ускорением по уравнению
v = u + при
Поскольку F = ma
а=Ф/м
Подставив это в приведенное выше уравнение
v=u+F/мт
Когда объект совершает круговое движение, скорость связана с ускорением соотношением
а=в2/r
Следовательно, скорость связана с силой уравнением
v2=Фр/м
Подробнее о Как определить конечную скорость без ускорения: факты, проблемы, примеры.
Часто задаваемые вопросы
Как ускорение зависит от времени и скорости?
Ускорение изменяется во времени и равно изменению скорости объекта во времени.
Ускорение зависит от времени и скорости объекта соотношением
v=u+at. Следовательно, a=vu/t
В чем разница между скоростью и скоростью?
Скорость — это скалярная величина, тогда как скорость — это векторная величина.
Скорость измеряется с точки зрения пути, пройденного объектом за время t, тогда как скорость не касается пути, пройденного объектом, а зависит от его начального и конечного положения.
Почему мы испытываем внезапный рывок назад при ускорении автомобиля?
При разгоне изменяется скорость движущегося автомобиля.
Изменение скорости одновременно изменяет импульс автомобиля и испытывает силу, которая ощущается на теле. Это может быть представлено соотношением как F=ma=mdv/dt=d/dt(mv)=dp/dt