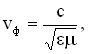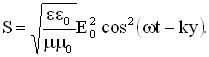Как определить скорость распространения волны по уравнению
274 дн. с момента
до конца учебного года
Длина волны. Скорость распространения волны.
Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
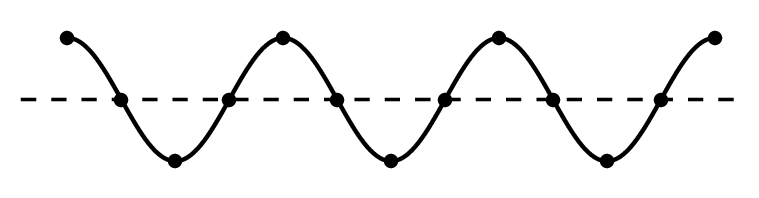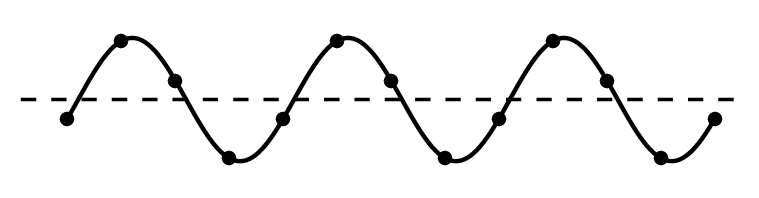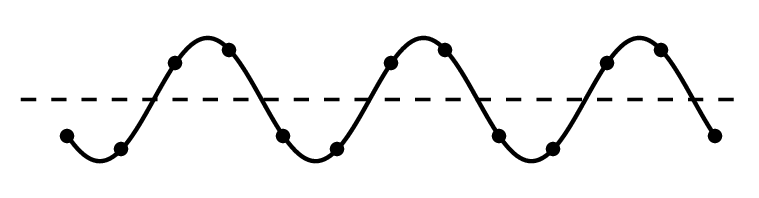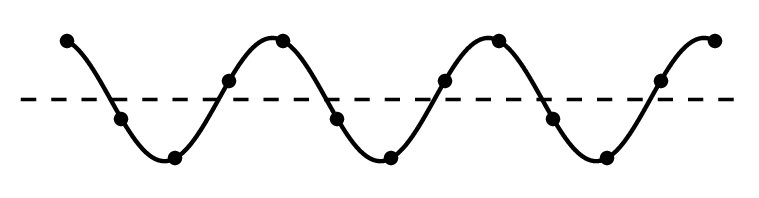
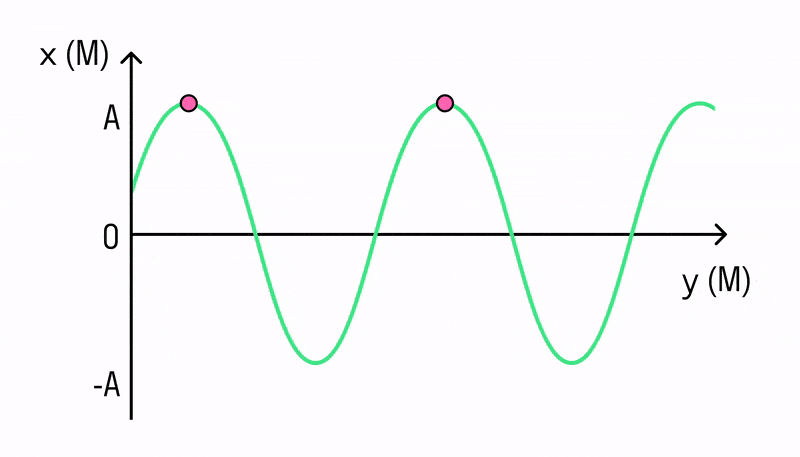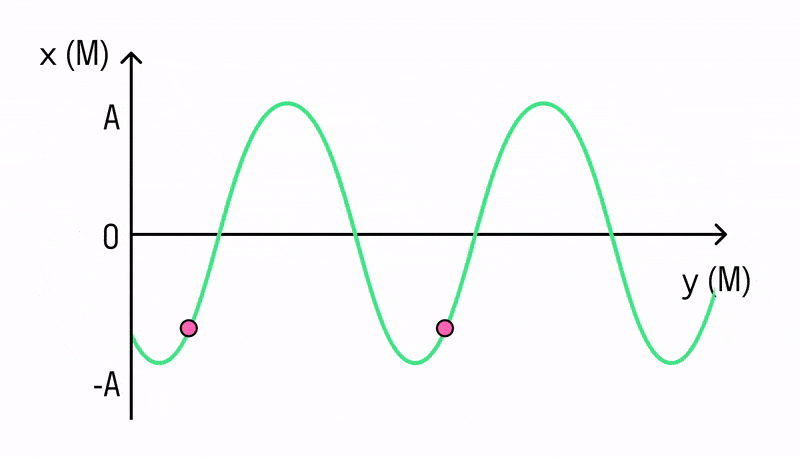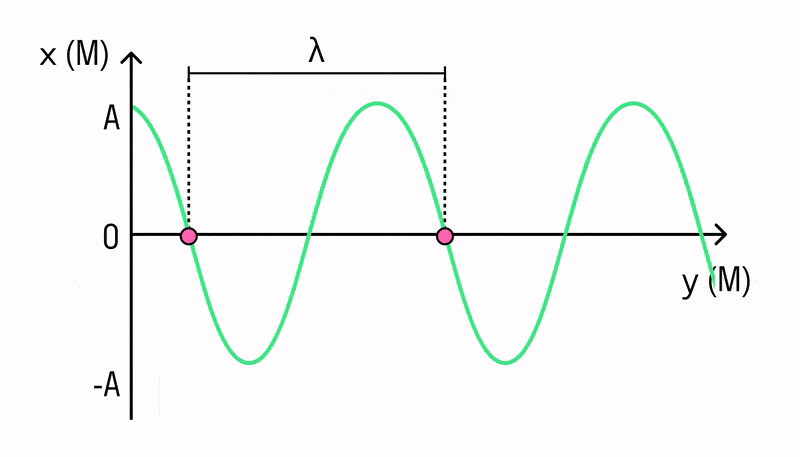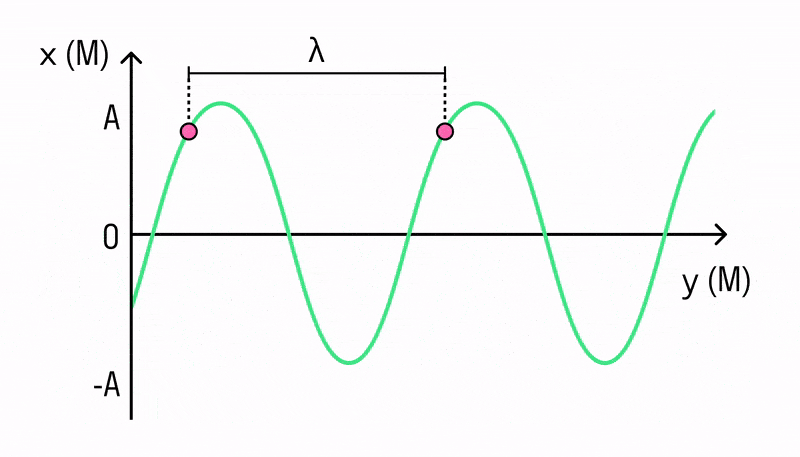
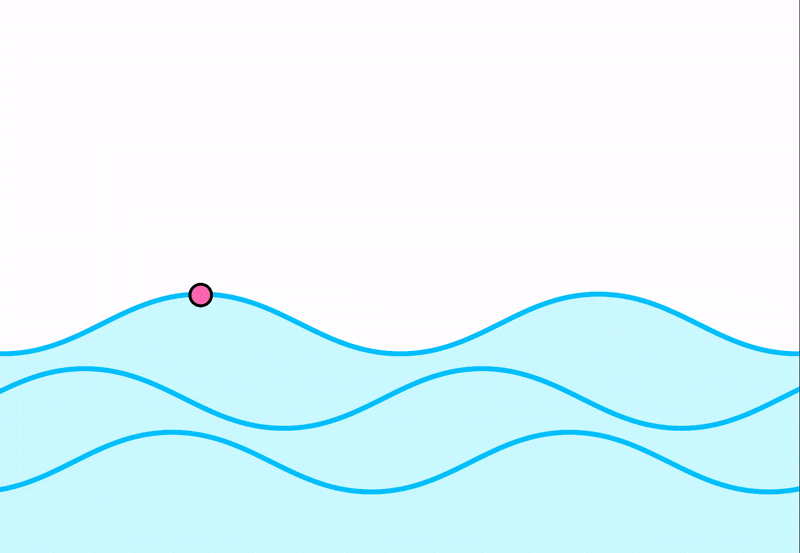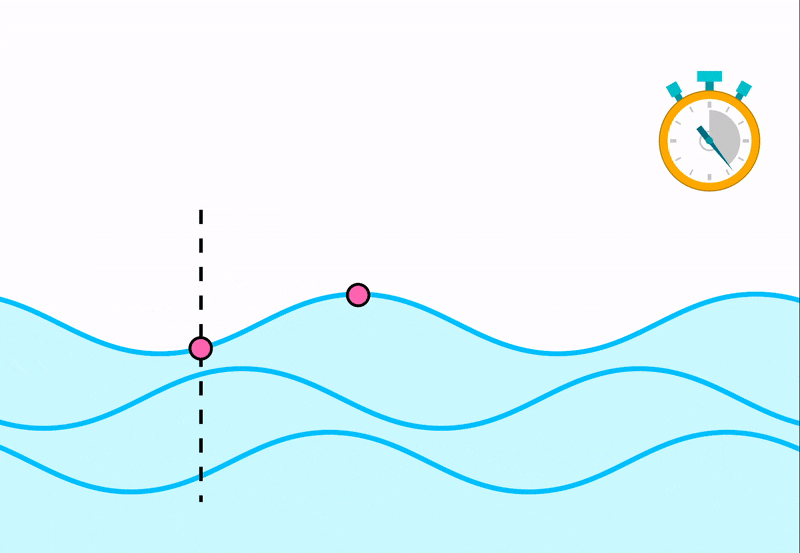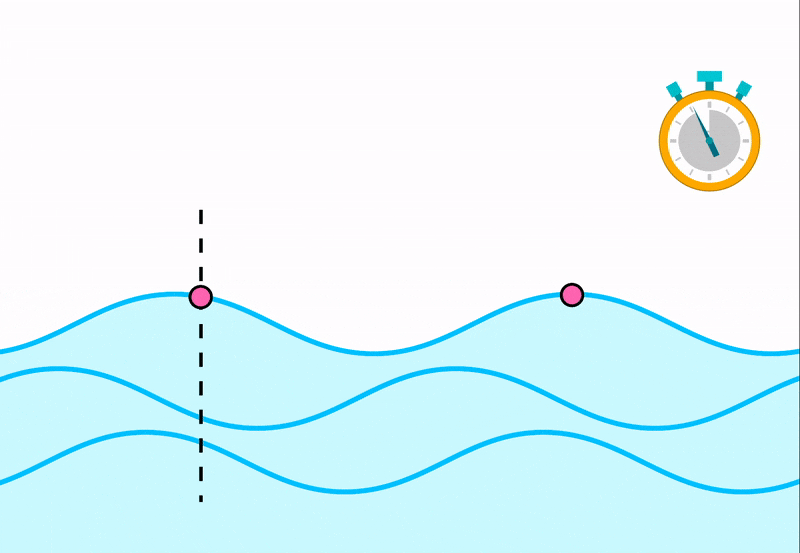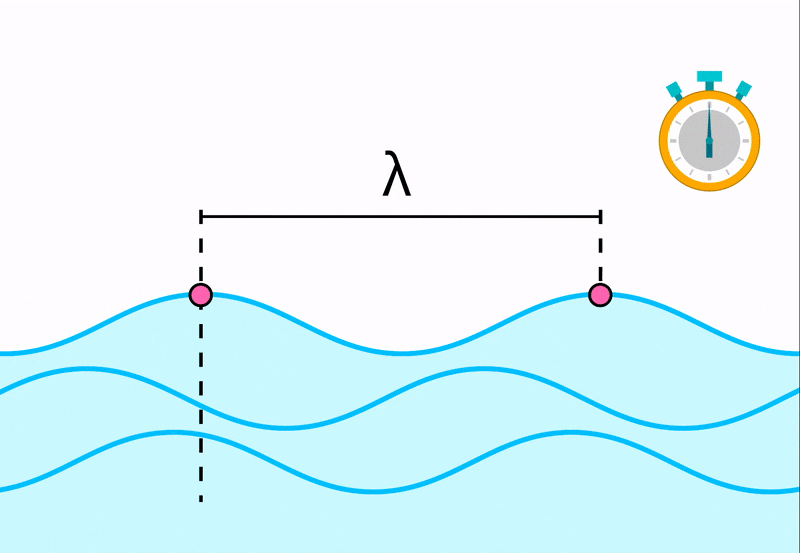
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
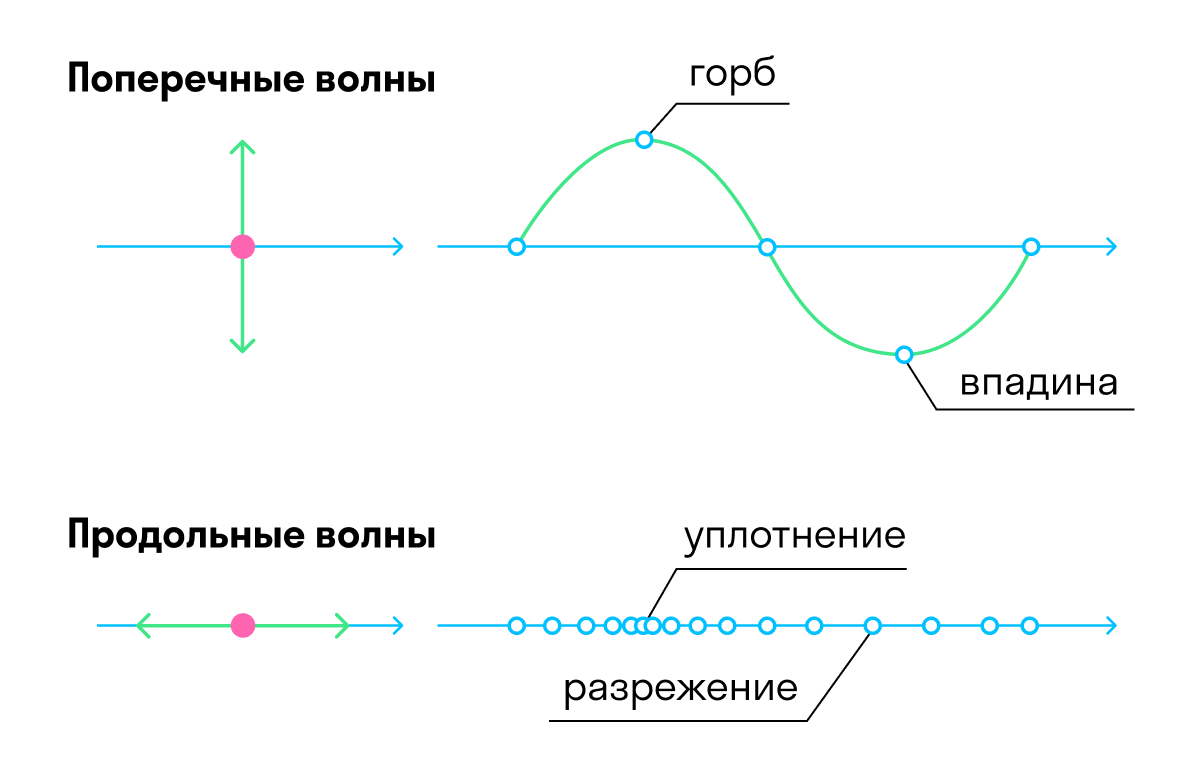
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λ = υ T . Так как период Т и частота v связаны соотношением T = 1 / v, то скорость волны:
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну:
длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [ λ ] = 1 м
скорость распространения волны [ v ] = 1м/с
период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц
Длина и скорость волны.
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
,
где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.
Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:
,
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
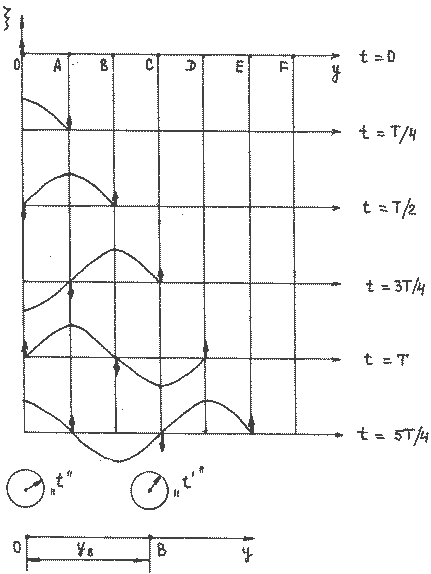
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Волновое движение в физике — формулы и определение с примерами
Содержание:
Волновое движение:
Процесс распространения колебаний в упругой среде называют механической волной. Для механических волн нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию, она должна обладать инертными и упругими свойствами.
Различают поперечные и продольные волны. Продольные волны могут распространяться в любых средах: твердых, жидких и газообразных; поперечные – только в твердых средах.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. Волны переносят энергию колебаний.
Изучив страницу, вы сможете:
- исследовать образование стоячих звуковых волн в воздухе;
- объяснять механизм образования стоячих волн, определять узлы и пучности, используя графический метод;
- исследовать интерференцию от двух источников на поверхности воды;
- объяснять принцип Гюйгенса и условия наблюдения дифракционной картины механических волн.
Уравнение бегущей волны
Колебательное движение тела в упругой среде является источником механической волны.
Волну, переносящую энергию, называют бегущей волной.
В однородной среде скорость распространения волны остается величиной постоянной. Смещение y (x, t) от положения равновесия частиц среды при распространении волны зависит от координаты x на оси 0х, вдоль которой распространяется волна, и от времени t по закону:
где
Введем волновое число тогда уравнение бегущей волны примет вид
Смещение точек упругой среды в волне, бегущей в противоположном направлении выбранной оси 0х, можно определить по формуле:
Вспомните! Основные характеристики волн. Волны, созданные источником, совершающим гармонические колебания, характеризуются амплитудой колебания частиц среды A, частотой длиной волны и скоростью распространения
Длиной волны называют расстояние между двумя соседними точками на оси 0х, колеблющимися в одинаковых фазах. Расстояние, равное длине волны , волна пробегает за период Т, следовательно, В однородных средах скорость распространения волны величина постоянная.
Физический смысл волнового числа
Запишем формулу (2), выразив циклическую частоту через период с учетом определения длины волны получим:
Бегущая волна обладает двойной периодичностью – во времени и в пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны Волновое число является пространственным аналогом циклической частоты
Фронт волны и волновая поверхность
Волна за время, равное периоду колебаний, достигает точек пространства, расположенных от источника на расстоянии длины волны. Совокупность этих точек представляет собой фронт волны, который отделяет колеблющиеся точки среды от точек, не вовлеченных в колебательное движение. Фронт волны от точечного источника представляет собой сферу, от плоской пластины – плоскость, от струны – форму цилиндра (рис. 79–81).
Фронт волны – это геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Направление распространения волны указывает луч, который перпендикулярен фронту волны.
В волне можно рассмотреть множество поверхностей, все точки которых совершают колебания синфазно, их называют волновыми поверхностями. При множестве волновых поверхностей, фронт волны только один.
Геометрическое место точек пространства, которые совершают колебания в одинаковой фазе в данный момент времени, называют волновой поверхностью.
Стоячие волны
Уравнение стоячей волны При отражении от более плотной среды волна, изменив свое направление на обратное, меняет фазу на то есть на противоположную. В результате сложения падающей и отраженной волн образуется стоячая волна. Она имеет вид, представленный на рисунке 83. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.
Получим уравнение стоячей волны путем сложения уравнений бегущих волн:
Заменив волновое число его значением запишем уравнение стоячей волны в виде:
Координаты точек пучностей и узлов определяются из условий наибольшего и наименьшего значений амплитуды. При образуется пучность с амплитудой равной 2 А (рис. 84). Расстояния от источника стоячей волны до пучностей равны:
При образуются узлы, амплитуда колебаний в этой точке равна 0. Расстояния от источника волны до узлов равны:
Расстояния между двумя соседними пучностями или двумя соседними узлами равны:
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не переносится в другие части струны. В каждом таком отрезке происходит дважды за период превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Отсутствие переноса энергии является отличительной особенностью стоячей волны.
Пример:
Уравнение бегущей волны, изображенной на рисунке (рис. 85): . Уравнение отраженной волны:
А. Получите уравнение стоячей волны как сумму падающей и отраженной волн.
В. Полученное выражение запишите, заменив волновое число и циклическую частоту через длину волны и период.
С. Определите положение узлов и пучностей.
Дано:
Решение: А. Уравнение стоячей волны определятся сложением уравнений бегущих волн:
В.
С. При образуется пучность с амплитудой 2А. Расстояние от источника до пучностей
С. Расстояние от узлов определим из условия тогда
Ответ:
Интерференция волн
Если в некоторой среде несколько источников возбуждают механические волны, то они распространяются независимо друг от друга. Все точки среды принимают участие в колебаниях, вызванных каждой волной в отдельности. Наложение волн, в результате которой появляется устойчивая картина чередующихся максимумов и минимумов колебаний частиц среды, называют интерференцией.
Интерферировать могут только волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Такие волны называют когерентными, их создают источники, колеблющиеся с одинаковой частотой и постоянным значением сдвига фаз.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Интерференция бывает стационарной и нестационарной. Стационарную интерференционную картину могут давать только когерентные волны: например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников (рис. 87).
Запомните! Волны называют когерентными, если их источники совершают колебания одной частоты с постоянным сдвигом фаз.
Условие максимума и минимума при интерференции двух волн
Амплитуда колебаний при наложении волн определяется в соответствии с принципом суперпозиции (рис. 88). Если в некоторой точке среды накладываются гребни когерентных волн, то происходит усиление колебаний, амплитуда принимает значение, равное сумме амплитуд. Если накладывается гребень одной волны с впадиной другой волны, то при равенстве амплитуд отдельно взятых волн данная точка пространства не совершает колебания. Если амплитуды отличаются, то колебания в этой точке совершаются с амплитудой равной разности амплитуд распространяющихся волн.
Для определения результата интерференции волн, распространяющихся от двух источников А и В, находящихся на расстоянии от точки С, достаточно определить разность хода волн и сравнить с длиной волны. Если разность хода равна целому числу длин волн, то в точке С произойдет наложение гребней или впадин, амплитуда колебаний возрастет (рис. 89). Выполняется условие максимума:
где − разность хода волн, – натуральное число, равное 0, 1, 2, 3 … Разность хода лучей соответствует разности фаз колебаний:
так как волна за период пробегает расстояние равное длине волны периоду Т соответствует фаза
Минимум колебаний в рассматриваемой точке среды наблюдается в том случае, если от двух когерентных источников распространяются волны со сдвигом фаз, равным нечетному числу p, а разность хода лучей кратна нечетному числу полуволн. В этом случае колебания происходят в противофазе (рис. 90).
Возьмите на заметку:
Интерференция волн приводит к перераспределению энергии колебаний между частицами среды. Это не противоречит закону сохранения энергии, так как в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.
Распространение волн. Принцип Гюйгенса – Френеля
На основе принципа Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, невозможно объяснить, почему источники вторичных волн создают фронт только по направлению распространения волны. Для объяснения явлений распространения волны французский физик О. Френель в 1815 г. дополнил принцип Х. Гюйгенса представлениями о когерентности и интерференции вторичных волн. При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается. Огибающая фронты вторичных волн является фронтом результирующей волны (рис. 92).
Дифракция механических волн
Вторичные волны, созданные точками среды, которые находятся на краю отверстия или препятствия, искривляются и волна огибает препятствие (рис. 93 а–г).
Дифракция – это явление огибания волнами препятствий.
Все волны способны огибать препятствия, если длина волны соизмерима с размерами препятствия. Дифракция становится заметной, если размеры препятствия меньше длины волны.
Физика в нашей жизни:
Струнные музыкальные инструменты
Интересно знать! Адырна (рис. 96 а) – один из древнейших казахских струнных инструментов. В его форме отобразилась воинственность кочевников-казахов: он напоминает изогнутый лук воина. Деревянный корпус инструмента легкий, так как он пустотелый. Струны изготавливают из кусков специально выделанной кожи или сплетенных из верблюжьей шерсти нитей. Музыкант играет, перебирая струны. Их в инструменте 13. Жетыген (рис. 96 б) – семиструнный музыкальный инструмент. Он имеет прямоугольную форму, изготовлен из дерева, струны – из конского волоса. Легенда о жетыгене раскрывает причину использования именно семи струн. Старик, потерявший семерых сыновей, вылил свое горе, исполняя кюи о них. Вспоминая каждого из сыновей, он натягивал новую струну на музыкальном инструменте.
Условие возникновения стоячей волны в струне
Стоячая волна в струне возникает только в том случае, если длина струны равняется целому числу длин полуволн:
Набору значений длин волн соответствует набор возможных частот Каждая из частот и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота называется основной частотой, все остальные частоты называются гармониками.
В отличие от груза на пружине или маятника, у которых имеется единственная собственная частота, струна обладает бесконечным числом собственных резонансных частот. На рисунке 96 в изображены несколько типов стоячих волн в струне. Стоячие волны различных типов могут одновременно присутствовать в колебаниях струны.
Визуализация звуковых волн
Существует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни (рис. 97). Немецкий физик Эрнст Хладни получал узор, посыпая пластинку песком и проводя по краю смычком. Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Песок скапливался и лежал неподвижно в узлах, а на участках, где отраженная волна усиливала бегущую, песок смещался.
Интересно знать! В Шотландии есть рослинская капелла св. Матвея, на одной из арок которой есть 213 резных каменных кубов, с вырезанным на них геометрическим рисунком. Многие исследователи пытались понять, что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел со своим сыном, пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни и пришли к выводу, что на кубах записаны ноты. Собрав ноты воедино и творчески обработав их, они представили миру произведение «Рослинский Мотет».
Итоги:
Глоссарий
Волновая поверхность – геометрическое место точек, имеющих одинаковую фазу колебаний.
Дифракция – явление огибания волнами препятствий.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Когерентные волны – волны, имеющие одинаковую частоту и постоянный сдвиг фаз.
Механическая волна – процесс распространения колебаний в упругой среде.
Фронт волны – геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Распространение колебаний в упругих средах. Продольные и поперечные волны
Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. В качестве примера достаточно вспомнить, что измерение пульса осуществляется на запястье, хотя сердце расположено внутри грудной клетки. Такие явления связаны с распространением механических волн.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме.
Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц за большой промежуток времени равно нулю.
Рассмотрим основные характеристики волны.
Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.
Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.
Основными характеристиками волны являются (рис. 208):
- амплитуда (A) — модуль максимального смещения точек среды из положений равновесия при колебаниях;
- период (T) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны);
- частота— число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;
- скорость— скорость перемещения гребня волны (это не скорость частиц!):
- длина волны— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника
Рассмотрим колебания источника волны, происходящие с циклической частотой и амплитудой А:
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией
где k — волновое число фаза волны.
Выражение х(t, r) называется уравнением плоской волны, распространяющейся (бегущей) вдоль направления радиус-вектора
Бегущую волну можно наблюдать, проведя следующий опыт: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна, описываемая уравнением плоской волны.
Рассмотрим классификацию бегущих волн по направлению колебаний частиц среды, в которой они распространяются.
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 209).
При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в воздухе и жидкости.
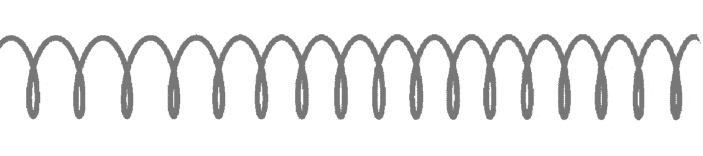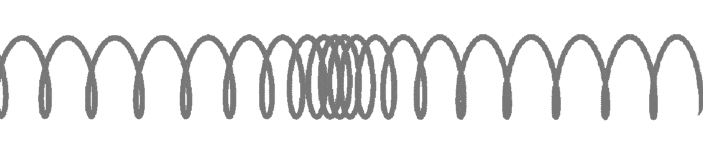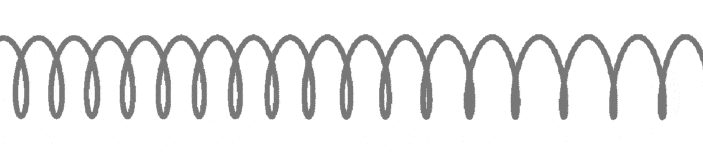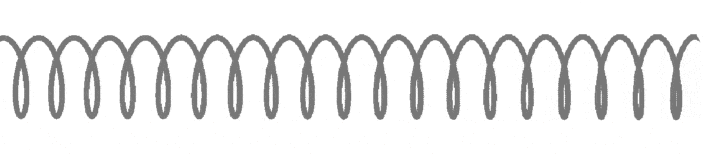
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. С помощью длинной пружины можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно пружине (рис. 210).
Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.
Продольные колебания симметричны относительно линии распространения ВС, и их действие на любой регистрирующий прибор не изменяется, если прибор будет поворачиваться вокруг направления распространения.
Действие поперечных волн на регистрирующий прибор зависит от того, в какой плоскости, проходящей через линию распространения, происходит колебание. Эта особенность поперечных волн носит название поляризации. Если колебания происходят в одной плоскости, то волну называют плоско или линейно поляризованной. Если конец вектора колебаний, например вектора смещения, скорости, напряженности электрического поля, описывает эллипс или окружность, то волну называют эллиптически или циркулярно-поляризованной.
До сих пор мы рассматривали волны, распространяющиеся в какой-либо среде. Волны, которые распространяются на границе раздела двух сред, называются поверхностными волнами. Примером данного типа волн служат волны на поверхности воды.
Звуковые волны. Скорость звука. Ультразвук
Звуком называются колебания среды, воспринимаемые органами слуха.
Раздел физики, в котором изучаются звуковые явления, называется акустикой.
Звуковая волна — упругая продольная волна, представляющая собой зоны сжатия и разрежения упругой среды (например, воздуха), распространяющиеся в пространстве с течением времени. Таким образом, в процессе распространения звуковой волны меняются такие характеристики среды, как давление и плотность.
Звуковые волны классифицируются по частоте следующим образом:
- инфразвук
- слышимый человеком звук
- ультразвук
- гиперзвук
Многие животные могут воспринимать ультразвуковые частоты. Например, собаки могут слышать звуки до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
Звуковые волны приносят человеку жизненно важную информацию — с их помощью мы общаемся, наслаждаемся мелодиями, узнаем по голосу знакомых людей. Мир окружающих нас звуков разнообразен и сложен, однако мы достаточно легко ориентируемся в нем и безошибочно можем отличить пение птиц от шума городской улицы.
Одной из важнейших характеристик звуковых волн является спектр. Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.
В сплошном спектре присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.
В
дискретном спектре — конечное число волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.
По типу спектра звуки разделяются на шумы и музыкальные тона.
Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).
Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию па различных музыкальных инструментах.
Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить
основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.
Любой звук, помимо частоты, характеризуется интенсивностью.
Интенсивность I — это энергия переносимая волной в единицу времени = 1 с через единичную площадку площадью расположенную перпендикулярно к направлению распространения волны:
Другими словами, интенсивность любой волны — мощность, переносимая волной через единичную площадку, расположенную перпендикулярно к направлению распространения волны.
Единицей интенсивности в СИ является ватт на метр в квадрате
Чтобы вызвать звуковые ощущения, волна должна обладать некоторой минимальной интенсивностью, называемой порогом слышимости.
С возрастом порог слышимости человека возрастает.
Интенсивность звуковых волн, при которой возникает ощущение боли, называют порогом болевого ощущения или болевым порогом. Интенсивность звука, улавливаемого ухом человека, лежит в широких пределах: от (порог слышимости) до (порог болевого ощущения). Человек может слышать и более интенсивные звуки, но при этом он будет испытывать боль.
Реактивный самолет может создать звук интенсивностью мощные усилители на концерте в закрытом помещении — до поезд метро — около
Уровни интенсивности звука L определяют обычно, используя шкалу, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б самый слабый звук, который воспринимает наше ухо. Единица названа в честь изобретателя телефона А. Г. Белла. Измерение уровня интенсивности в децибелах проще, поэтому принято в физике и технике.
Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле
где I — интенсивность данного звука, — интенсивность соответствующая минимально возможной интенсивности звука, улавливаемого ухом человека.
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.
Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это связано с тем, что восприятие звука — процесс не только
физический, но и физиологический. Действительно, человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).
Основными физиологическими характеристиками звука являются громкость, высота и тембр.
Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах, т. е. его способностью улавливать звуки различных частот. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 Гц до
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://www.calc.ru/Dlina-I-Skorost-Volny.html
http://www.evkova.org/volnovoe-dvizhenie-v-fizike
Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) — это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ — фаза волны; $k=frac{2pi }{lambda }$ — волновое число; $lambda $ — длина волны; $omega $ — циклическая частота; $varphi $ — начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ — период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны — это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ — модуль объемной упругости вещества; $rho =const$ — плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ — показатель адиабаты; $p$ — давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ — модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ — модуль сдвига среды; $rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период — величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.
Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.
Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.
Электромагнитные волны — это те волны, которые мы потрогать не можем.
- Например, радиоволны, Wi-Fi и свет.
Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 108 м/с. И источники у них разные.
Волны также принято делить на продольные и поперечные:
Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
Морская волна — продольная или поперечная?
На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
- λ — длина волны [м]
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны
T = t/N
T — период [с]
t — время [с]
N — количество колебаний [—]
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
𝑣 = S/t
𝑣 — скорость [м/с]
S — путь [м]
t — время [с]
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
𝑣 = λ/T
𝑣 — скорость [м/с]
λ — длина волны [м]
T — период [с]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
- Возьмем формулу скорости:
- Нам известна длина волны, но не дан период. Период вычисляется по формуле:
- Теперь подставляем величины в формулу
𝑣 = λ/T
T = t/N
T = 40/10 = 4 с
𝑣 = λ/T
𝑣 = ¼ = 0,25 м/с
Ответ: 𝑣 = 0,25 м/с
Резонанс
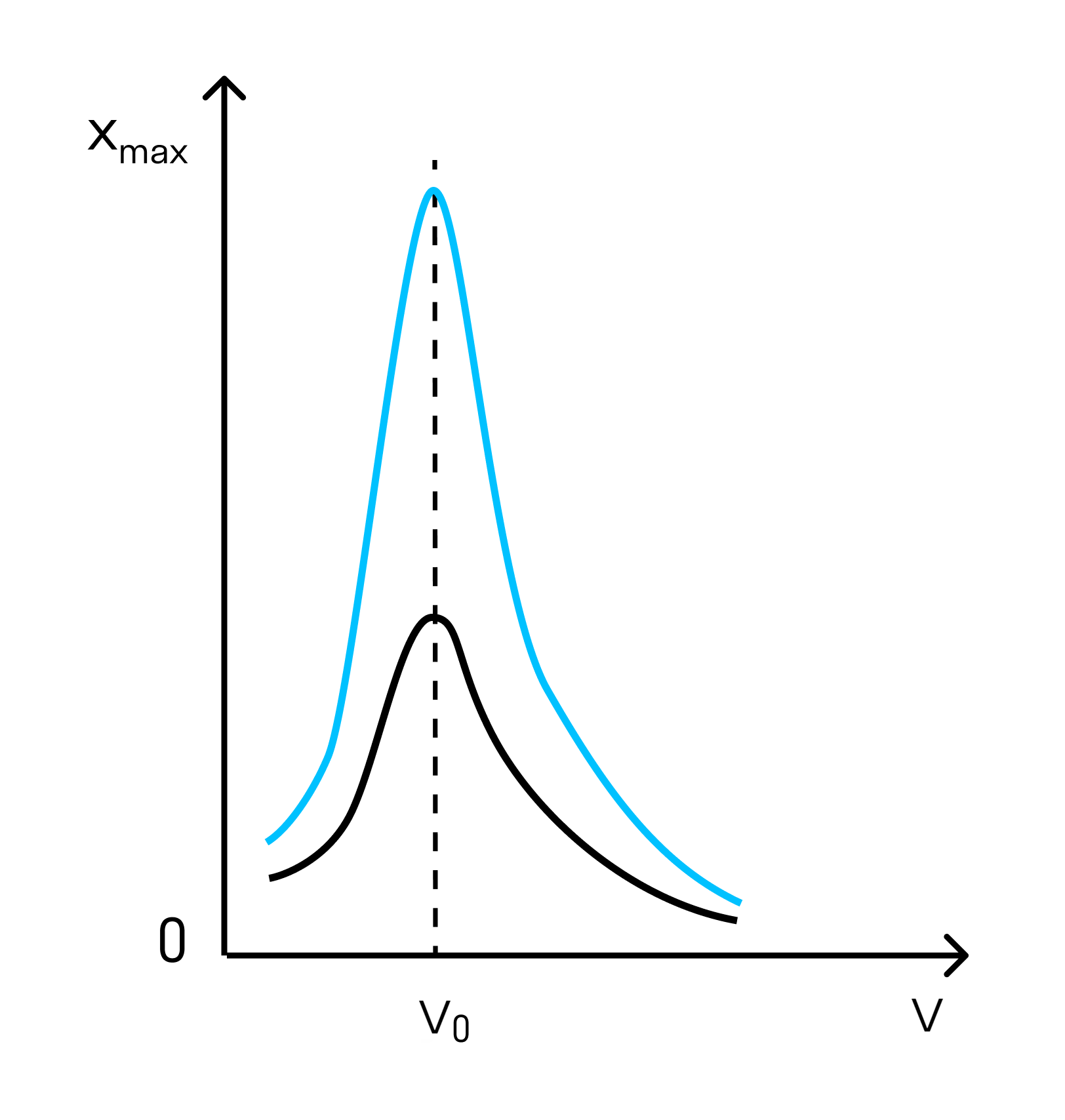
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
ν — частота [Гц]
t — время [с]
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
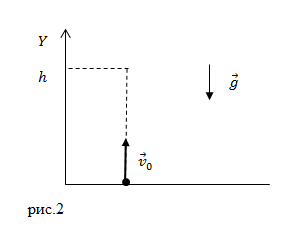
«Бросая
в воду камушки,
смотри
на круги, ими образуемые,
иначе
такое бросание
будет
пустою забавою»
Козьма
Прутков
Задача
1.
уравнение бегущей волны имеет вид ).
Найдите частоту волны, скорость её распространения и длину.
|
ДАНО: |
РЕШЕНИЕ Запишем уравнение бегущей волны в общем виде По условию задачи задано уравнение Сопоставляя эти два уравнения можно определить, что Циклическую частоту также можно рассчитать по формуле Тогда частота волны Длину волны можно рассчитать по формуле |
|
|
Ответ:
= 1 Гц,
= 4 м/с,
= 4 м.
Задача
2.
В воздухе звук проходит 1,1 км на 2,6 с медленнее, чем в воде. Принимая
скорость звука в воздухе равной 330 м/с, определите скорость звука в воде.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем формулу, по которой Исходя из этого, запишем Преобразуем последнюю формулу и выразим из неё скорость |
|
|
Ответ:
1500 м/с.
Задача
3.
Два человека бросают разные камни в воду на разное расстояние от берега, но
волны приходят к берегу одновременно. Расстояние между двумя ближайшими
гребнями волны от первого камня равно 2 см, а расстояние между двумя ближайшими
гребнями волны от второго камня — 2,5 см. Найдите соотношение расстояний, на
которые были брошены камни, если известно, что обе волны имеют одинаковую
частоту.
|
ДАНО: |
РЕШЕНИЕ Пройденный путь можно рассчитать по формуле
Используя соотношение, Скорость распространения волны определяется как С учётом данной формулы пройденные расстояния могут быть Тогда отношение пройденных расстояний равно |
|
|
Ответ:
второй камень был брошен на расстояние в 1,25 раза большее, чем первый.
Задача
4.
бегущая по шнуру волна распространяется со скоростью 30 см/с. Известно,
что в момент времени t = 2 с
центральная точка шнура в первый раз отклоняется от положения равновесия в
положительном направлении на максимальное расстояние. Найдите длину шнура, если
длина бегущей волны равна 2 см.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем уравнение бегущей волны в общем виде Циклическая частота определяется по формуле Скорость распространения волны равна Тогда циклическая частота будет определяться по формуле Запишем уравнение для Необходимо обратить Преобразуем данное уравнение |
|
|
Ответ:
119 см.
Задача
5.
Навстречу друг другу едут два автомобиля с сиренами. Первый автомобиль едет со
скоростью 45 м/с и частота колебаний его сирены равна 500 Гц, а второй
автомобиль едет со скоростью 50 м/с и частота колебаний его сирены составляет
550 Гц. Водитель какого автомобиля будет слышать более высокий звук? Какова
будет частота этого звука? Скорость звука в воздухе принять равной 330 м/с.
|
ДАНО: |
РЕШЕНИЕ Для простоты рассмотрим Автомобиль является Скорость распространения волны Запишем закон сложения скоростей Таким образом, в системах В соответствии с этим, Необходимо обратить внимание, |
|
|
Ответ:
водитель первого автомобиля услышит более высокий звук, частота которого
составит 708,3 Гц.
1. Упругие волны
1.1. Упругие продольные и поперечные волны
1.2. Характеристики бегущих волн
1.2.1. Длина волны
1.2.2. Фазовая скорость волны
1.2.3. Фазовая скорость различна для разных сред
1.2.4. Фронт волны. Волновая поверхность
1.2.5. Уравнение бегущей волны
1.2.6. Волновое уравнение
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
1.3. Энергия упругих волн
1.4. Принцип суперпозиции волн. Групповая скорость
1.5. Интерференция волн. Стоячие волны
2. Звуковые волны
3. Электромагнитные волны
Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.
Процесс распространения колебаний в пространстве называется волной.
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.
1. Упругие волны
1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.
Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.
Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.
Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.
Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.
1.1. Упругие продольные и поперечные волны
Все волны делятся на продольные и поперечные.
Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.
Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.
Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.
1.2. Характеристики бегущих волн
1.2.1. Длина волны
Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.
Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна
).
Если точки разделены расстоянием , их колебания происходят в противофазе.
1.2.2. Фазовая скорость волны
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.
Фазовая скорость — это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны , фазовой скорости
и периода колебаний Т задается соотношением:
.
Учитывая, что , где
— линейная частота волны,
— период, а циклическая частота волны
, получим разные формулы для фазовой скорости:
.
Для волнового процесса характерна периодичность по времени и по пространству.
Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой:
. Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом:
.
Таким образом. Можно добавить еще одно уравнение для фазовой скорости:
.
1.2.3. Фазовая скорость различна для разных сред
В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
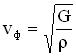
где — модуль сдвига среды,
-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
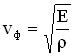
где Е — модуль Юнга, — плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением: 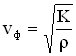
где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, — плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой: 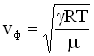
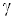
— молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (
) и от его термодинамического состояния (Т).
1.2.4. Фронт волны. Волновая поверхность
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
Если известно положение фронта волны в некоторый момент времени и скорость волны , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
1.2.5. Уравнение бегущей волны
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О — центр (источник) колебаний, она колеблется по закону:
,
где — смещение точки О от положения равновесия,
— частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.
Через промежуток времени процесс колебаний дойдет до точки В, и она будет колебаться по закону:
.
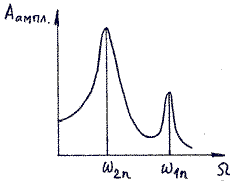
Рисунок 2.1.1.
Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и
связаны между собой соотношением
или
. Расстояние между точками О и В обозначим
. Фазовая скорость волны равна
, тогда
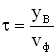
и
и формулы
и
, можно записать уравнение колебаний точки В в разных видах:
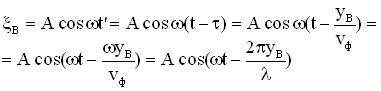
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:
,
где — волновое число (см. определение выше).
Это уравнение и есть уравнение для смещения любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина
— фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.
Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.
Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:
.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.
1.2.6. Волновое уравнение
Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:
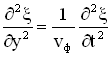
— фазовая скорость волны.
Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что есть функция двух переменных t и y.
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
,
то скорость этой точки есть величина , а ускорение —
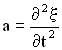
,
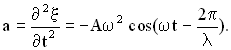
1.3. Энергия упругих волн
В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме равна:
, где
— объемная плотность среды.
Если выбранный объем записать как , где S – площадь его поперечного сечения, а
— его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком
через его поверхность:
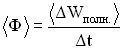
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.
Эта величина определяется соотношением:
,
где 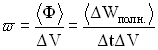
— фазовая скорость волны. Так как фазовая скорость волны
— вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:
.
Величина , вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.
Интенсивностью волны называется модуль среднего значения вектора Умова 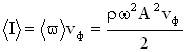
1.4. Принцип суперпозиции волн. Групповая скорость
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
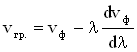
1.5. Интерференция волн. Стоячие волны
1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.
В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна
, т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.
Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.
2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники и
испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника
, а от второго —
.
Колебания точки М под действием волн от двух источников и
описываются уравнениями:
,
. Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”):
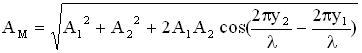
), если
, где
Величина
называется разностью хода двух волн. Условие максимума при интерференции имеет вид:
. Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (
), если
, (
). Условие минимума при интерференции имеет вид:
. Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид:
,
Суммарное смещение
частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений
и
:
.
Это и есть уравнение стоячей волны. Величина 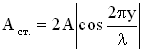
) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.
В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:
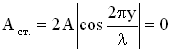
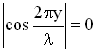
для
Итак, координаты узлов задаются формулой:
.
Расстояние между двумя соседними узлами равно .
Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:
.
Это уравнение можно получить из условия максимума амплитуды
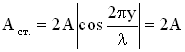
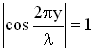
(
).
Расстояние между двумя соседними пучностями равно .
4. Изменение фазы волны при ее отражении.
Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на
радиан соответствует появлению дополнительного хода луча, равного
.
2. Звуковые волны
1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.
Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.
2. Избыточное звуковое давление. Уравнение звуковой волны.
Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.
Если — давление и плотность невозмущенной среды (среды, по которой не проходит волна), а
— давление и плотность среды при распространении в ней волнового процесса, то величина
называется избыточным давлением. Величина
есть максимальное значение избыточное давление (амплитуда избыточного давления).
Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:
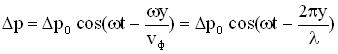
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.
Если ввести величину избыточной плотности и ее амплитуды
так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так:
. 3. Объективные и субъективные характеристики звука.
Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.
К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.
Таблица 3.
| Субъективные Характеристики | Объективные характеристики |
| Высота звука | Высота звука определяется частотой волны |
| Тембр (окраска звука) | Тембр звука определяется его спектром |
| Громкость (сила звука) | Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды) |
Остановимся на некоторых определениях.
Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.
Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).
Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.
Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.
3. Электромагнитные волны
1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.
Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:
где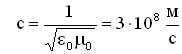
,
— электрическая и магнитная постоянные,
,
— соответственно диэлектрическая и магнитная проницаемость среды.
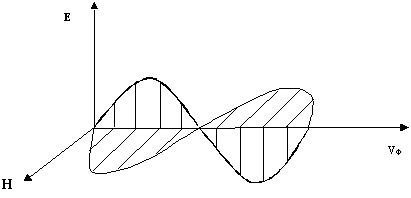
2. Электромагнитные волны — поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).
Для сравнения ориентации тройки векторов , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.
Рисунок 2.1.4
Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
Такие волны называются плоско (или линейно) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).
4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.
Стоячая электромагнитная волна состоит из двух стоячих волн — магнитной и электрической, колебания которых сдвинуты по фазе на .
5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: 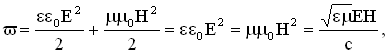
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
соответственно объемная плотность энергии этой волны
Значение объемной плотности энергии волны меняется за период от 0 до .Среднее за период значение энергии равно:
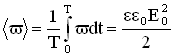
6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова — Пойнтинга:
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны: — фазовая скорость волны,
среднее значение объемной плотности энергии поля волны.
Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.