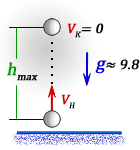
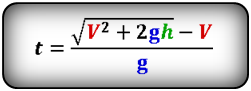
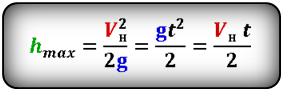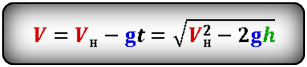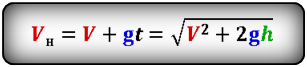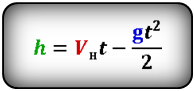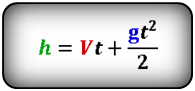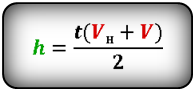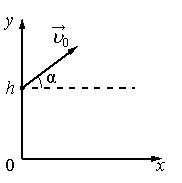Как найти скорость с которой бросили мяч - Исправление недочетов и поиск решений вместе с Examum.ru

1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту

h_max
— максимальная высота достигнутая телом за время t

V_к — конечная скорость тела на пике, равная нулю

V_н — начальная скорость тела

t — время подъема тела на максимальную высоту h

g ≈ 9,8 м/с² — ускорение свободного падения

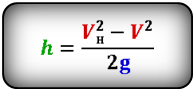
Формула максимальной высоты (h_max):

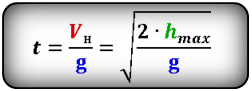
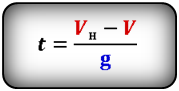
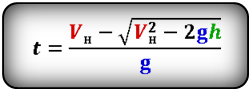
Формула времени за которое тело достигло максимальную высоту (t):

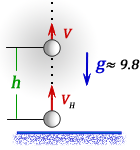
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести

h — расстояние пройденное телом за время t

V_н — начальная скорость тела

V — скорость тела в момент времени t

t — время подъема за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Формула скорости тела в момент времени t (V):

Формула начальной скорости тела (V_н):

Формулы высоты тела в момент времени t (h):

Формулы времени, за которое тело достигло высоту h (t):

Подробности

Опубликовано: 04 августа 2015

Обновлено: 13 августа 2021

Источник

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

v_min = v₀cosα = v_h

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

v_max = v_o = v

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

l = s_x = v_0xt_полн = v₀cosα t_полн

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀cosα, данная формула принимает вид:

x = v₀cosα t

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

v₀sinα = gt_под

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

Важные факты!

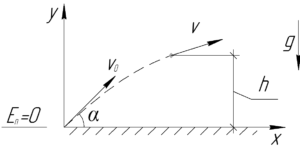
График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

t_полн = t_пад + t_под

Уравнение координаты x:

x = v₀cosα t

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Задание EF17562

С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.

Алгоритм решения

1.Записать исходные данные.

2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.

3.Выбрать нулевой уровень для определения потенциальной энергии.

4.Записать закон сохранения энергии.

5.Решить задачу в общем виде.

6.Подставить числовые значения и произвести вычисления.

Решение

Запишем исходные данные:

• Время падения стального шарика: t = 0,4 c.

• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.

• Угол наклона плиты: α = 30^о.

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p

Потенциальная энергия шарика в точке А равна:

E_pA = mgH

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

EpB=mgl1

Перед ударом кинетическая энергия шарика равна:

EkB=mv22

Согласно закону сохранения энергии:

EpA=EpB+EkB

mgH=mgl1+mv22

Отсюда высота H равна:

H=mgl1mg+mv22mg=l1+v22g

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h−l1=v2sin2β2g=v2sin2(90−2α)o2g

Отсюда:

l1=h−v2sin2(90−2α)o2g

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

v=gt

Следовательно:

H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g

H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)

H=1,4−10·0,422(sin2(90−60)o−1)

H=1,4−5·0,16(sin230o−1)

H=1,4−0,8((12)2−1)=1,4−0,8(14−1)

H=1,4+0,6=2 (м)

Ответ: 20

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17980

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Установить вид механического движения, исходя из условий задачи.
Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
Определить, как зависят эти величины от времени.
Установить соответствие между графиками и величинами.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

Ответ: 42

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18741

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

v_x = v₀ cosα

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 43.3k

Источник

Условие задачи:

Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча на высоте – 10 м. Сопротивлением воздуха пренебречь.

Задача №2.8.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(upsilon_0=20) м/с, (h=10) м, (upsilon-?)

Решение задачи:

Эту задачу можно решать разными способами: либо используя методы кинематики, либо используя законы сохранения энергии. Причем второй способ более быстрый, поэтому выберем его.

Понятно, что по закону сохранения энергии полная механическая энергия мяча будет сохраняться, так как нет сил сопротивления воздуха.

[E = const]

Кинетическая энергия камня в момент броска равна сумме кинетической и потенциальной энергии камня на некоторой высоте.

[{E_{к1}} = {E_{к2}} + {E_{п2}}]

Кинетическая энергия тела в любой точке определяется по формуле ({E_к} = frac{{m{upsilon ^2}}}{2}), где (upsilon) – скорость тела в этой точке, а потенциальная – по формуле ({E_п} = mgh), где (h) – высота над землей в этой точке. Тогда:

[frac{{mupsilon _0^2}}{2} = frac{{m{upsilon ^2}}}{2} + mgh]

[upsilon _0^2 = {upsilon ^2} + 2gh]

[upsilon = sqrt {upsilon _0^2 – 2gh} ]

Численно скорость мяча на высоте 10 м равна:

[upsilon = sqrt {{{20}^2} – 2 cdot 10 cdot 10} = 14,1; м/с = 51; км/ч]

Ответ: 51 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.22 Подъемный кран поднимает груз массой 8 т на высоту 15 м. Определить время
2.8.24 Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной

Источник

Мяч брошен вертикально вверх Каковы его скорость и ускорение?

В высшей точке скорость частицы равна нулю и ее ускорение равно ускорению свободного падения действует в нисходящем направлении. 4 июня 2014 г.

Какова скорость и ускорение мяча, брошенного вверх?

Если вы бросите мяч вверх со скоростью 9,8 м/с, скорость будет равна 9,8 м/с в направлении вверх. Теперь мяч находится под действием силы тяжести, которая на поверхности Земли заставляет все свободно падающие объекты испытывать вертикальное ускорение –9,8 м./с2.

Когда мяч брошен вертикально вверх, его скорость и ускорение будут равны?

В высшей точке скорость частицы нуль и его ускорение равно ускорению силы тяжести, действующей в направлении вниз.

При броске мяча вертикально вверх его ускорение равно?

Как сказано выше, это ускорение есть не что иное, как ускорение свободного падения, вызванное гравитационным притяжением или силой, действующей со стороны Земли на шар. Его значение обычно принимают за 9,8 м/с^2.

Чему равно ускорение мяча, брошенного вверх?

Ответ: Вы подбросили мяч прямо вверх, поэтому его направление остается вверху. … Во время движения мяча вверх, а затем вниз ускорение постоянно, 9,8 м/с2 (ускорение свободного падения). Направление движения мяча таково, что он поднимается, останавливается, а затем снова опускается.

Какова скорость мяча, брошенного вертикально вверх в высшей точке?

ноль Вопрос: Когда мяч брошен вертикально вверх, он продолжает движение вверх, пока не достигнет определенного положения, а затем падает вниз. В этой высшей точке, его скорость мгновенно равна нулю.

См. также объяснение того, как инверсия магнитного поля свидетельствует о расширении морского дна.

Когда мяч брошен вертикально вверх на максимальную высоту, его скорость равна нулю?

Скорость частицы на максимальной высоте равна ноль, потому что это поворотный момент. Ускорение действует на частицу на всем пути и направлено вниз.

Какова начальная скорость мяча, брошенного вверх?

9,8 м/с2 Вопрос: Мяч, брошенный вертикально вверх, достигает максимальной высоты 30 м над поверхностью Земли. На максимальной высоте скорость мяча равна: Ответ: 0 м/с. Мгновенная скорость любого снаряда на максимальной высоте равна нулю.

…

Объекты, запущенные вверх.

Переменная	Ценность
в	0 м/с
Δу	НАЙТИ
а	-9,8 м/с2
т	0,40 с

Когда мяч брошен вертикально вверх на максимальную высоту, его скорость равна нулю, а значит, на частицу не действует ускорение?

Ответ: вариант г правильный.. хотя на максимальной высоте скорость равна нулю, все равно есть ускорение, потому что даже тогда земля притягивает его и действует на него силой, а ускорение зависит от силы, которая исходит из второго закона Ньютона. .

Когда мяч брошен вертикально вверх со скоростью v0?

Когда мяч брошен вертикально вверх со скоростью v0, достигает максимальной высоты h. Если кто-то хочет утроить максимальную высоту, то мяч должен быть брошен со скоростью.

Как найти скорость подброшенного вверх мяча?

Как найти ускорение брошенного мяча?

Как найти скорость тела, брошенного вверх?

Скорость тела, брошенного вертикально вверх, уменьшается от максимального значения до нуля через некоторое время tu. Если начальная скорость обозначена как vi, нулевая скорость произошла в момент времени, равный tu, то уравнение скорости имеет вид v = vi — (г * т) где g = ускорение свободного падения, равное 9,8 м/с^2.

Чему равна конечная скорость мяча?

Конечная скорость мяча равна в_ф = -14,7 м/с, принимая вниз, чтобы быть отрицательным направлением. Время от момента отрыва мяча от руки ребенка до момента его удара о землю составляет 2,00 с.

Когда мяч брошен вертикально вверх, его скорость в высшей точке мгновенно становится равной нулю, ускоряется ли мяч, находясь в высшей точке?

В самой верхней точке скорость действительно нуль. Однако после этого он моментально меняется. Если бы ускорение было равно нулю, скорость мяча не изменилась бы, и он навсегда остался бы в воздухе. Ускорение – это скорость изменения скорости.

Смотрите также, что использовал Христофор Колумб для навигации

Когда тело брошено вертикально вверх, какова его конечная скорость?

Ответ: когда тело брошено вертикально вверх, его конечная скорость при достижении максимальной высоты будет равно нулю.

Когда тело брошено вертикально вверх, чему равна его скорость в высшей точке, равное ускорению тела?

Поскольку ускорение из-за гравитационной силы постоянно действует вниз, и это является причиной того, что скорость нуль в высшей точке, следовательно, скорость равна нулю из-за ускорения.

Когда мяч достигнет максимальной высоты, какова его скорость?

0 м/с Когда снаряд достигает максимальной высоты, вертикальная составляющая его скорости равна мгновенно ноль (v_у = 0 м/с).

Что произойдет, если мяч подбросить вертикально вверх на максимальную высоту?

Тело, брошенное вертикально вверх, замедляется под действием земного притяжения. Его скорость уменьшается до тех пор, пока он достигает максимальной высоты, где скорость равна нулю. Затем он равномерно ускоряется вниз под действием силы тяжести.

Когда мяч брошен вертикально вверх, гравитационная потенциальная энергия мяча?

Когда мяч брошен вертикально вверх, кинетическая энергия энергии мяча превращается в потенциальную энергию мяча. Но полная энергия шара остается постоянной во время его движения. Так что вариант 1 правильный. Это потому, что в начале мяч имеет высокую кинетическую энергию и не имеет потенциальной энергии.

Мяч, брошенный вертикально вверх, пролетит расстояние 19,6 м?

Таким образом, начальная скорость мяча равна 19,6 м/с Это означает, что мяч был брошен вверх со скоростью 19,6 м/с. Таким образом, мячу требуется 2 секунды, чтобы достичь самой высокой точки земли. Другими словами, мячу потребуется в общей сложности 2+2=4 секунды, чтобы вернуться к бросающему.

Когда частица брошена вертикально вверх, ее скорость на одной трети ее максимальной высоты составляет 10 корней 2 метра в секунду. Максимальная высота, которую она достигает, равна?

Когда частица брошена вертикально вверх, ее скорость на одной трети максимальной высоты составляет 10√2 м/с. Максимальная высота, достигнутая им. (1) 20√2 м.

Чему равно ускорение мяча по величине и направлению в тот момент, когда мяч находится на максимальной высоте?

Причиной ускорения мяча является сила тяжести. Все время, пока мяч находится в воздухе, его ускорение вниз составляет 9,8 м/с2 при условии, что это происходит на поверхности Земли. Обратите внимание, что ускорение может быть либо 9,8 м/с2, либо -9,8 м/с2.

…

Объекты, запущенные вверх.

Переменная	Ценность
т	0,40 с

Что произойдет, если предмет бросить вертикально вверх?

Студенты должны всегда помнить, что для вертикального движения тела вверх знак ускорения свободного падения должен быть отрицательным и что для движения вниз знак ускорения свободного падения должен быть положительным.

Как называется выброс предмета вертикально вверх в высшей точке тела?

Когда вы подбрасываете мяч в воздух, его скорость уменьшается, пока он на мгновение не остановится в самом верху движения мяча. Его ускорение −9,8 мс−2 в самом верху, так как тело движется вверх против силы тяжести. Другими словами, ускорение свободного падения g=9,8 мс-2↓.

Каково ускорение тела, брошенного вверх в высшей точке?

В высшей точке снаряда его скорость равна нулю. В высшей точке снаряда, его ускорение равно нулю. Скорость изменения положения begin{align*}xend{align*} меняется со временем по пути снаряда.

Каково ускорение тела в его высшей точке при броске вверх?

если частица брошена вертикально вверх, то в высшей точке скорость равна нулю, поэтому ускорение, действующее на тело в высшей точке, будет равно г.= соотв..

Каковы будут скорость и ускорение шарика вверх на максимальной высоте?

На максимальной высоте скорость становится равной нулю. Следовательно, скорость наверху равна нулю, а ускорение равно ускорению силы тяжести (g).

Когда предмет брошен вертикально вверх, действует сила тяжести?

Ускорение силы тяжести равно 9,8 м/с² .

На какую максимальную высоту поднимется тело, брошенное вверх со скоростью 19,6 м/с, если G = 9,8 м с2?

Какой максимальной высоты достигнет тело, брошенное вверх со скоростью 19,6 м/с, примем G 9,8 М с2? Таким образом, камень 1 может достичь максимальной высоты 19,6 метра за 2 секунды от земли, если его бросить в 19. 6 м/с.

Как доказать, что время подъема равно времени спуска?

1 ответ

Время спуска t1 секунд, конечная скорость объекта v м/с. Пройденное расстояние будет таким же, как если бы предмет был брошен вверх.
Из уравнения (1) и (2) мы видим, что u = v.
т1 = т. время подъема = время спуска.

См. также, как военачальники получили власть в городах-государствах.

Когда частица брошена вертикально вверх, ее скорость составляет одну треть от ее?

Когда частица брошена вертикально вверх, ее скорость на одной трети максимальной высоты равна 10√2 м/с.

Когда частица брошена вертикально вверх, ее скорость составляет одну четвертую максимальной высоты?

Его скорость на четверти максимальной высоты равна 20 мс−1.

Каково ускорение тела, брошенного вертикально?

Мяч брошен вертикально вверх со скоростью 25,0 м/с. а) На какую высоту он поднимается? (б) Как долго

Теория предмета, брошенного вертикально вверх

Подброшенный вверх мяч, какова его скорость и ускорение на вершине?

Движение снаряда мяча, брошенного вверх | Уровень физики

Источник

Подбросим мяч вертикально вверх. Он поднимется на какую-то высоту, после чего упадет вниз.

Земля притягивает мяч, значит на мяч действует нескомпенсированная сила притяжения. Как гласит второй закон Ньютона, скорость мяча из-за этого меняется.

Движение тела под действием силы тяжести, называется свободным падением. Когда тело падает свободно, оно испытывает невесомость.

Для удобства будем рассматривать отдельно свободное движение мяча вверх и, его свободное падение вниз.

Движение вверх

Рассмотрим рисунок 1. В левой части рисунка — 1а) изображено движение мяча вверх, а в правой – 1б) – движение вниз. Сплошным кружком обозначено начальное положение мяча, а пунктирным – конечное. Красными стрелками обозначена скорость мяча на различных высотах.

Рис. 1. Свободное движение мяча вверх и вниз под действием силы тяжести

При движении вверх скорость тела уменьшается, так как вектор ускорения и вектор скорости направлены в противоположные стороны (рис. 1а). Движение вверх равнозамедленное.

Выражение для скорости при движении мяча вверх:

[ large v_{y} = v_{0y} — g cdot t_{text{вверх}} ]

Вертикальное перемещение мяча при его движении вверх выражается такой формулой:

[ large h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} ]

В верхней точке траектории скорость мяча будет равна нулю. Эта точка для движения вверх будет конечной, а для движения вниз – начальной.

Поэтому, для движения вверх нулю равна конечная скорость мяча (v_{y}=0), а для движения вниз – его начальная скорость (v_{0y}=0).

Движение вниз

При движении вниз – наоборот, скорость будет увеличиваться, так как векторы скорости и ускорения сонаправлены (рис. 1б). Движение вниз равноускоренное.

Выражение для скорости при движении мяча вниз:

[ large v_{y} = v_{0y} + g cdot t_{text{вверх}} ]

Вертикальное перемещение при движении вниз выражается формулой:

[ large h = v_{0y} cdot t_{text{вверх}} + g cdot frac{t_{text{вверх}}^2}{2} ]

Таким образом, под действием силы тяжести мяч движется по вертикали, меняя свою скорость.

Пока мяч находится в полете, он не давит на опору и не растягивает подвес. Проще говоря, он находится в невесомости (ссылка) – то есть, не имеет веса.

Масса есть всегда, а вес тела (ссылка) может отсутствовать! Кроме того, одна и та же масса в различных ситуациях может обладать разным весом.

Из рисунка 1 так же, следует, что

если тело при падении вернется на уровень, с которого оно стартовало, то:

— скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет ( large left|vec{v_{0y}} right|= left|vec{v_{y}} right|) ;

— время подъема равняется времени спуска ( large t_{text{вверх}} = t_{text{вниз}} );

Когда перемещение вверх не равно перемещению вниз

Рассмотрим теперь следующий рисунок. На рисунке 2а представлен случай, когда путь, пройденный вверх больше пути, пройденного при движении вниз. Предположим, мы подбросили мяч вертикально вверх и, он упал на крышу какого-то строения, например, гаража.

Рис. 2. Пути, скорости и время свободного полета вверх и вниз будут различаться

В таком случае на подъем потребуется больше времени, чем на спуск

[ t_{text{вверх}} > t_{text{вниз}} ]

И скорость, с которой мяч подбрасывали вверх будет больше скорости, с которой мяч ударится о крышу

[ left|vec{v_{0y}} right|> left|vec{v_{y}} right|]

На рисунке 2б путь при движении вверх меньше пути вниз. Такое может быть, если мы заберемся на крышу гаража и, находясь на крыше, подбросим мяч вертикально вверх.

Теперь на спуск мяча до земли потребуется больше времени, чем на подъем

[ t_{text{вверх}} < t_{text{вниз}} ]

И скорость, с которой мяч ударится о землю, окажется больше скорости, с которой мы его подбрасывали вверх, находясь на крыше гаража.

[ left|vec{v_{0y}} right|< left|vec{v_{y}} right|]

Примечания:

Все тела, независимо от их массы, на планету падают с единым ускорением свободного падения (vec{g});
Ускорение (vec{g}) не является постоянной величиной, оно может меняться;
У различных планет и других небесных тел ускорение (vec{g}) отличается от земного;
На различных высотах над Землей ускорение (vec{g}) будет разным;
Из-за вращения Земли на экваторе ускорение (vec{g}) меньше, чем на полюсах.

Источник