Как найти скорость сближения решения

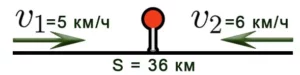
Если они движутся в одном направлении, объекты могут находиться как близко, так и далеко друг от друга. В этом случае они как бы «конкурируют» за общую дистанцию и «действуют друг против друга». Поэтому их общая скорость равна их разности скоростей.

Решение задач на движение. Формулы, схемы, встречное движение

Очень легко рисовать диаграммы для задач на движение. Они помогают визуализировать проблему и найти правильное решение. В сложных случаях или если ученик не может найти решение, рекомендуется дополнить диаграмму таблицей, в которой параметры скорости, времени и расстояния указаны в заголовке. Подробнее об этом ниже.

1. Простые задачи на движение
2. Решение
3. Обратные задачи на движение
4. Как найти скорость, если известно время и расстояние
5. Как найти время, когда известны скорость и расстояние
6. Схемы задач на встречное движение
7. Решение
8. Задачи на движение в одном направлении
9. Шпаргалка по решению задач на скорость, время и расстояние

Простые задачи на движение

Простые задачи о путешественниках, лыжниках, мотоциклистах и других движущихся объектах (есть даже задачи о черепахах) решаются уже в первых классах. На этих примерах легко понять, как составлять диаграммы.

Задача 1. Он прибыл в пункт B через 3 часа. Он дошел до точки А. Он шел со скоростью 5 км/ч. Каково расстояние между этими двумя точками?

Постройте диаграмму для решения задачи: Прямая линия, соединяющая точки A и B, является общим расстоянием. Стрелка показывает направление движения путешественника. Над стрелкой укажите скорость, если она известна. Поместите время или расстояние ниже (или выше) сегмента:

Если вы не смогли решить задачу с помощью диаграммы, я предлагаю вам воспользоваться таблицей:

Скорость	Время	Расстояние
5 км/ч	3 ч	? км

Чтобы решить задачу с помощью таблицы, запомните правила:

• Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
• Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы: V = S : t )
• чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы: t = S : t

Решение

5 x 3 = 15 км — расстояние между пунктами A и B.

Обратные задачи на движение

Как найти скорость, если известно время и расстояние

Чтобы не запутаться в различных условиях задачи, составьте задачу в обратном порядке по сравнению с первым примером:

Задача 2: Расстояние между пунктами A и B равно 15 км. Путешественник преодолел это расстояние за 3 часа. С какой скоростью ехал путешественник?

Скорость	Время	Расстояние
? км/ч	3 ч	15 км

Как найти время, когда известны скорость и расстояние

Задача 3 Расстояние между двумя точками равно 15 км. Пешеход двигался со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти все расстояние?

Скорость	Время	Расстояние
5 км/ч	? ч	15 км

Решение простых задач на движение: скорость, время и расстояние

В простых задачах на движение обычно имеется движущийся объект, для которого необходимо определить неизвестную величину: Скорость, время или расстояние. В этом случае формула применяется в своем первоначальном виде:

Задача 1. Автомобиль двигался со скоростью 85 км/ч в течение 2 часов. Первое задание дается в первой форме. Определите расстояние. Решение: Вычислите расстояние по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.

Задача 2: Велосипедист проехал 60 км за 5 часов. Определите скорость. Решение: Рассчитайте скорость велосипедиста по следующей формуле: V = S:t = 60 км : 5 ч = 12 км/ч.

Задача 3: Мотоциклист проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он ехал со скоростью 15 км/ч. Сколько времени ему понадобилось, чтобы преодолеть это расстояние? Решение: Рассчитайте время в пути мотоциклиста

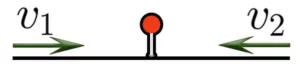
Когда они движутся в противоположных направлениях, скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью разделения. Скорость разделения определяется по следующей формуле:

При решении таких задач лучше всего нарисовать схему движения, чтобы облегчить решение.

Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)

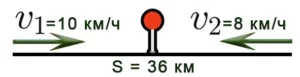
Задача 5: Два велосипедиста отправились в путь одновременно, чтобы встретиться в двух пунктах, расстояние между которыми 36 км. Скорость первого велосипедиста составляет 10 км/ч, а скорость второго велосипедиста — 8 км/ч. Через сколько часов они встретятся? Решение: 1) Определите скорость приближения: V = 10+8 = 18 км/ч. 2) Определите время: t = S:V = 36 : 18 = 2 ч.

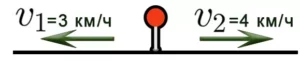
Задача 6: Два пешехода одновременно выходят из одного и того же места в противоположных направлениях. Скорость первого пешехода — 3 км/ч, второго — 4 км/ч. Каким будет расстояние между ними через 30 минут? Решение. 3) Найдите расстояние: S=V × t = 7 × 0,5 = 3,5 км.

Задача 7. Два автобуса одновременно выехали из двух пунктов, расстояние между которыми 300 км, на встречу. Они встретились через 2 часа. Найдите скорость второго автобуса, если первый автобус движется со скоростью 70 км/ч. Решение. 1) Мы знаем расстояние и скорость, поэтому найдите скорость по формуле. Это скорость конвергенции. 2) Определим скорость второго автобуса: 150-70 = 80 км/ч.

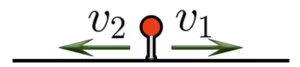
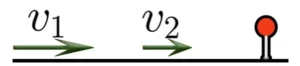
Когда два объекта движутся в одном направлении и один объект «догоняет» другой, расстояние между ними уменьшается. Скорость сближения в таком движении определяется по формуле:

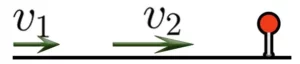
Когда два объекта движутся в одном направлении и один объект «отстает» от второго, расстояние между ними увеличивается. Скорость отделения в этом типе движения определяется по следующей формуле: Если объект движется в стоячей воде, расстояние между объектами увеличивается:

Если объект движется в стоячей воде (озере), его скорость называется скоростью самого объекта. То есть скорость объекта равна собственной скорости объекта.

Решение задач на движение в одном направлении: сближение и удаление

Обратите внимание, что плот — это тело, скорость которого равна нулю (V=0). Таким образом, плот может плыть только по течению и со скоростью течения.

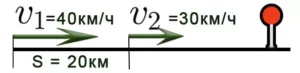
Проблема 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль движется со скоростью 40 км/ч, второй автомобиль движется со скоростью 30 км/ч. Через сколько часов первый автомобиль доедет до второго автомобиля? Решение. 1) Найдите скорость сближения машин.

2) Найдите время для расстояния (20 км) и скорости приближения (10 км/ч): 20:10=2 часа.

Задание 9. автомобиль

Задачи на движение в одном направлении

• Задачи на скорость сближения
• Задача на скорость удаления

Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.

Задачи на скорость сближения

Скорость сближения — это скорость, с которой объекты сближаются друг с другом.

Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Задача на скорость удаления

Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.

Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.

Памятка «Учимся решать задач на движение»

В задачах на движение  рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

S = V ● t

Скорость  — это частное от деления расстояния на время движения

V = S : t

Время – это частное от деления расстояния на скорость движения

t = S : V

Задачи на встречное движение

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

 Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

Схема к задаче:

 

Решение:

S = V ● t

V сближ. = 1V + 2V

1 способ:

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

2 способ:

1) 12 + 14 = 26 (км/ч) – скорость сближения

2) 26 • 3 = 78 (км)

Ответ: расстояние между посёлками 78 км.

 Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

Схема к задаче:

 

Решение:

V сближ. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ: машины встретятся через  2 часа.

 Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

Схема к задаче:

 

Решение:

V = S : t

2V = V сближ. — 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ: 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. 

V удал. = 1V + 2V

 Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

Схема к задаче:

 Решение:

S = V ● t

1 способ

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

3)36 + 42 = 78 (км) 

2 способ

V удал. = 1V + 2V

S = V ● t

1)12 + 14 = 26 (км/ч) – скорость удаления

2)26 • 3 = 78 (км)

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

 Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

Схема к задаче:

 

Решение:

V удал. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

Схема к задаче:

  

Решение:

V = S : t

2V = V удал. — 1V

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.

Математика

5 класс

Урок № 35

Задачи на движение

Перечень вопросов, рассматриваемых в теме:

1. Понятия скорости, времени, расстояния.
2. Формулы нахождения скорости, времени, расстояния.
3. Понятия скорости сближения, скорости удаления.

Глоссарий по теме

Расстояние – это длина от одного пункта до другого.

Большие расстояния, в основном, измеряются в метрах и километрах.

Расстояние обозначается латинской буквой S.

Чтобы найти расстояние, надо скорость умножить на время движения:

S = v ∙ t

Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Скорость обозначается латинской буквой v.

Чтобы найти скорость, нужно расстояние разделить на время движения:

v = S : t

Время – это продолжительность каких-то действий, событий.

Время движения обозначается маленькой латинской буквой t.

Чтобы найти время, нужно расстояние разделить на скорость движения:

t = S : v

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010

Дополнительная литература

1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014

2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.

3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010

Теоретический материал для самостоятельного изучения

Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.

Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.

Рассмотрим задачу:

Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?

Решение:

Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.

Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:

200 м : 50 с = 4

Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч). 

У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:

200 м : 50 с = 4 (м/с)

Скорость движения первого школьника составляет 4 метра в секунду.

Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:

200 м : 100 c = 2 (м/с)

Скорость движения первого школьника – 4 (м/с).

Скорость движения второго школьника – 2 (м/с).

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.

Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.

Рассмотрим задачу:

От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?

Решение:

Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:

1200 : 600 = 2 (мин)

Ответ: мы доедем до спортивной секции за 2 минуты.

Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

S = v ∙ t

Рассмотрим задачу:

Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?

Решение:

Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:

v = 60 (м/мин)

t = 15 (минут)

S = v ∙ t = 60 ∙ 15 = 900 (метров)

Ответ: мы прошли 900 метров.

Если известно время и расстояние, то можно найти скорость:

v = S : t

Рассмотрим задачу:

Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?

Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:

S = 800 метров

t = 8 минут

v = S : t = 800 : 8 = 100 (м/мин)

Ответ: скорость школьника была 100 м/мин.

Если известна скорость и расстояние, то можно найти время:

t = S : v

Рассмотрим задачу:

От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?

Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?

Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:

S = 600 метров

v = 120 (м/мин)

t = S : v = 600 : 120 = 5 (минут).

Ответ: мы дойдём до спортивной секции за 5 минут.

Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.

Задачи на сближение.

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Задача.

Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.

Решение:

1. Найдём скорость сближения велосипедистов:

13 км/ч + 15 км/ч = 28 км/ч

1. Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:

28 ∙ 3 = 84 км

Ответ: расстояние между населёнными пунктами 84 км.

Задачи на скорость удаления.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Рассмотрим задачу:

С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?

Решение:

1. Определим скорость удаления. Для этого сложим их скорости:

60 + 130 = 190 км/ч.

Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.

1. Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:

190 ∙ 2 = 380 км.

Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.

Задачи на движение объектов в одном направлении.

В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Рассмотрим задачу:

Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?

Решение:

1. Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:

130 км/ч − 90 км/ч = 40 км/ч

1. Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:

40 ∙ 3 = 120 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.

Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.

Задача.

Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Решение:

1. Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:

90 ∙ 3 = 270 метров

1. Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:

85 ∙ 3 = 255 метров

1. Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):

900 + 255 = 1155 м

1155 – 270 = 885 м

Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):

900 – 270 = 630 м

630 + 255 = 885 м

Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.

1. Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?

В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:

90 ∙ 1 = 90 м

85 ∙ 1 = 85 м

900 + 85 – 90 = 985 – 90 = 895 м

Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:

90 ∙ 3 = 270 м

85 ∙ 3 = 255 м

900 + 255 – 270 = 1155 – 270 = 885 м

Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.

А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:

900 : 5 = 180 минут.

Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

	S	v	t
1.	135 км	9 км/ч	____ ч
2.	____ м	12 м/с	4 с
3.	132 м	____ м/мин	11 мин

Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:

1. Надо найти время: t = S : v

135 : 9 = 15 часов.

1. Надо найти расстояние: S = v ∙ t

12 ∙ 4 = 48 м.

1. Надо найти скорость: v = S : t

132 : 11 = 12 м/мин.

Верный ответ:

	S	v	t
1.	135 км	9 км/ч	15 часов
2.	48 м	12 м/с	4 с
3.	132 м	12 м/мин	11 мин

№2. Тип задания: единичный / множественный выбор

Выберите верный ответ к задаче:

Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?

Варианты ответов:

1. 70
2. 30
3. 270
4. 240

Эта задача относится к типу задач на сближение, т.е. нам надо:

1. сложить скорости мотоциклиста и автомобилиста:

60 + 30 = 90 км/ч – скорость сближения;

1. узнать, сколько километров они пройдут за 3 часа вместе. Для этого:

90 ∙ 3 = 270 км;

1. из общего расстояния нам осталось вычесть пройденное:

300 – 270 = 30 км

Верный ответ: 2. 30 км.

Для решения задач на движение по прямой используется одна основная формула:

где:

• Скорость (V) — расстояние, пройденное за единицу времени.
• Время (t) — время в пути.
• Расстояние (S) — пройденный путь, или расстояние.

Зная эту формулу (для расстояния), вы можете легко  вывести из неё формулу для скорости, или времени.

Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.

Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.

Все задачи на движение делятся на следующие типы:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решение простых задач на движение: скорость, время и расстояние

В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:

Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние. 
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.

Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.

Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь? 
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.

В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах,  то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.

Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.

Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)

При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:

При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле: 

При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.

Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся? 
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.

Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.

Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.

Решение задач на движение в одном направлении: сближение и удаление

Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:

Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:

Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.

Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.

Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.

2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.

Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.

Решение задач на движение по реке

Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:

• по течению реки → скорость увеличивается;
• против течения реки → скорость уменьшается.

Таким образом, в задачах рассматривают 2 скорости: 

• Скорость собственная — Vs;
• Скорость течения реки — Vt.

Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается. 
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.

Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится. 
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.

Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок? 
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.

Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt  – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt  – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону:  t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону:  t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.

Больше задач на движение Ваш ребёнок может решить, скачав программы:

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Полезные советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
• При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.