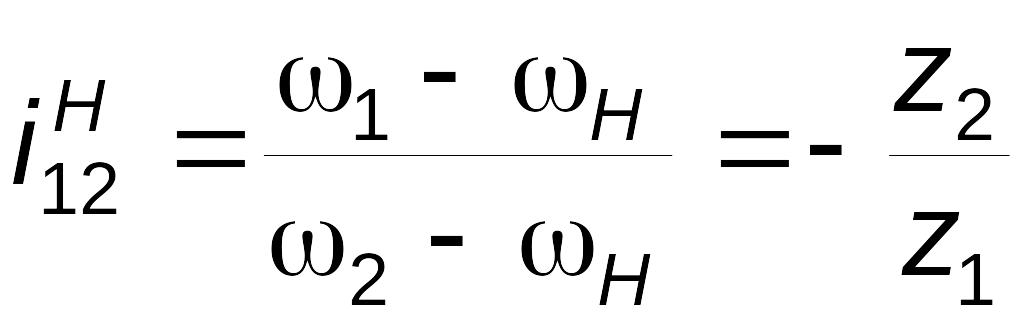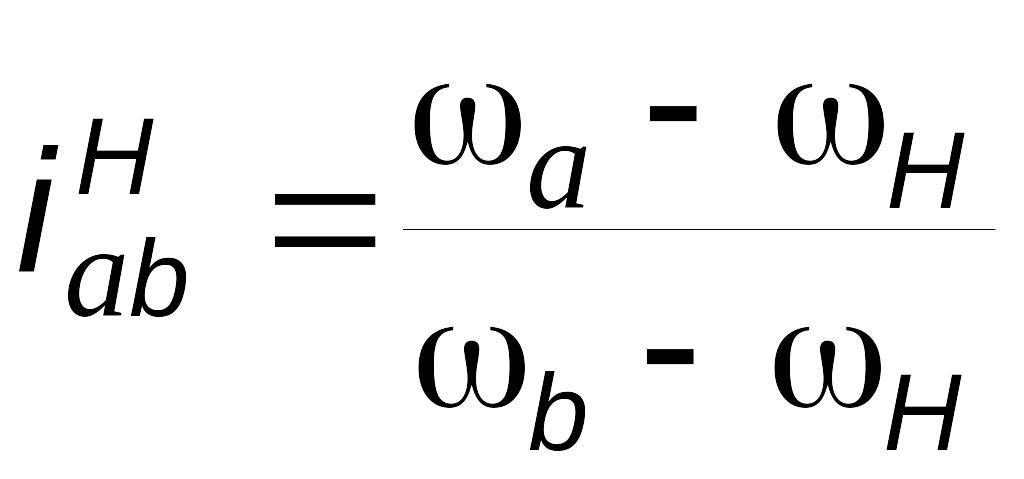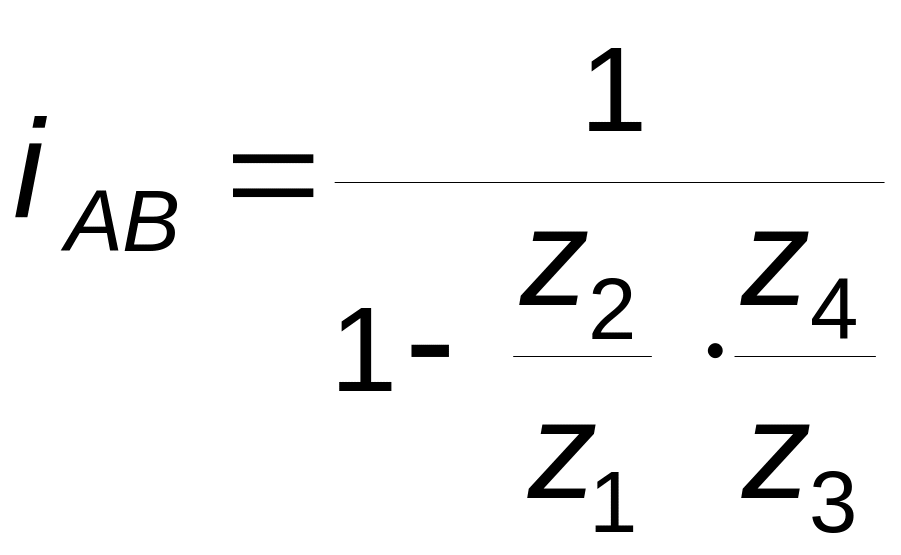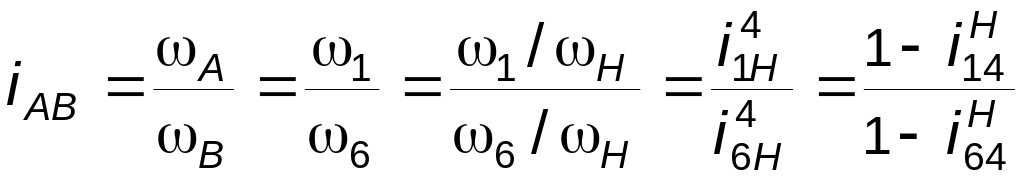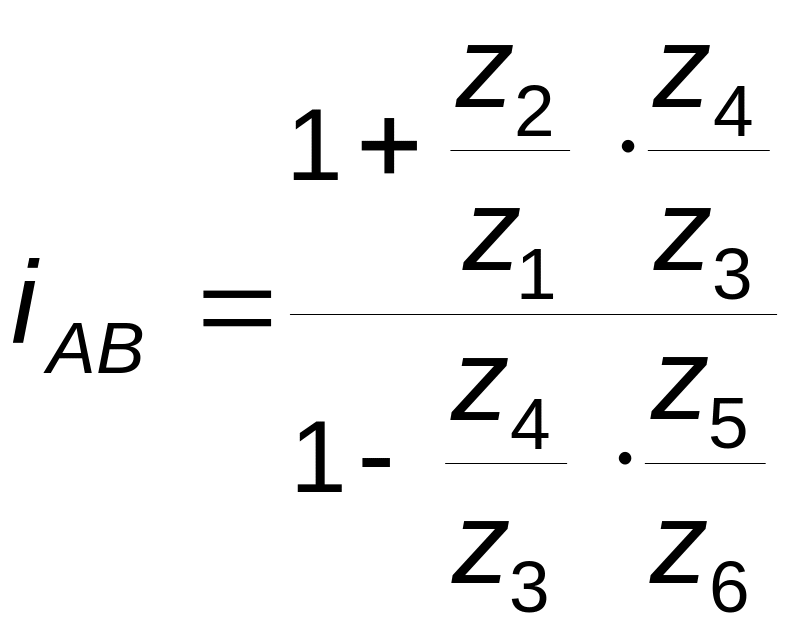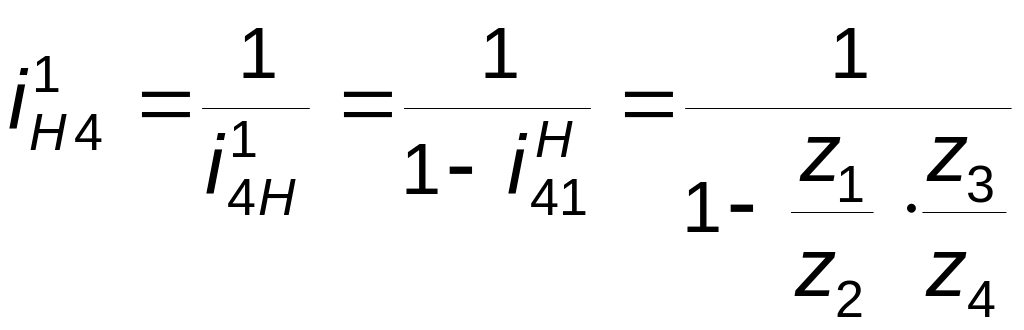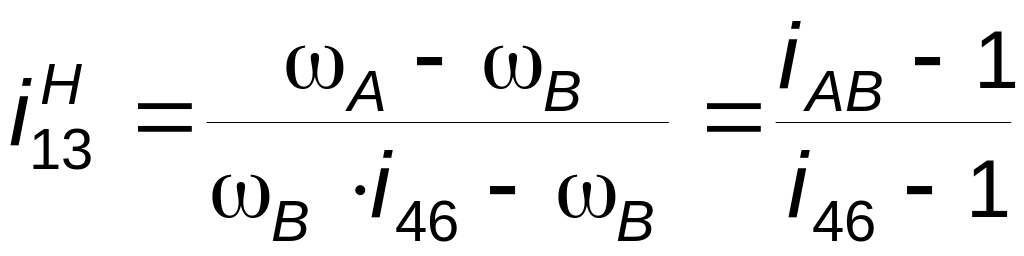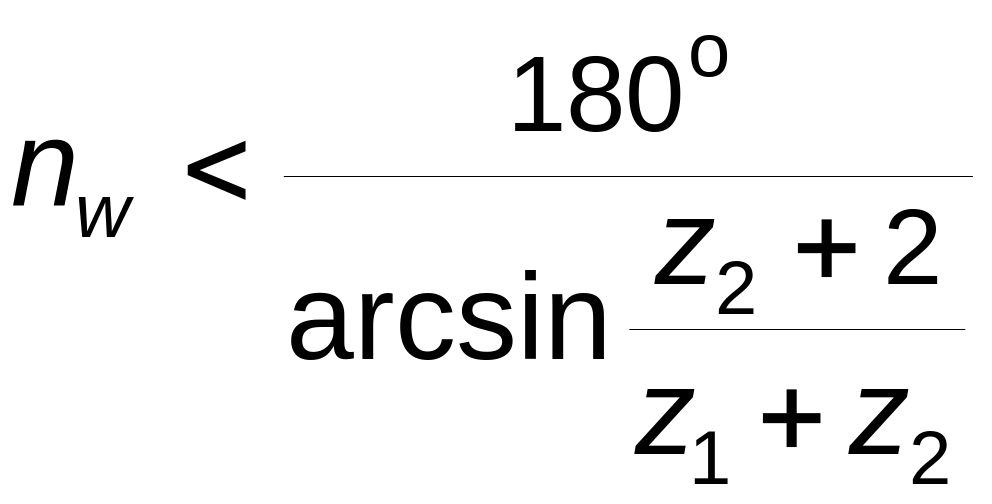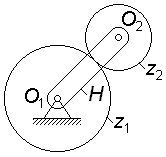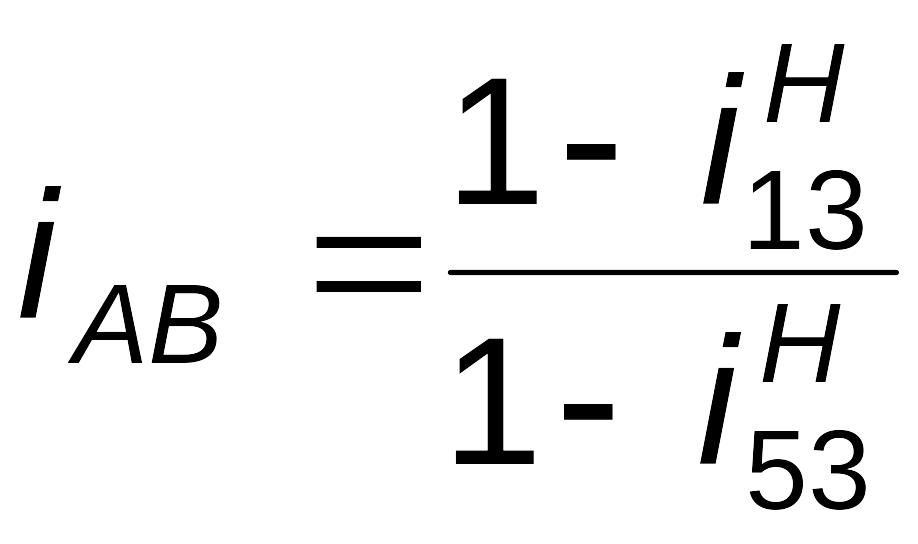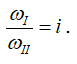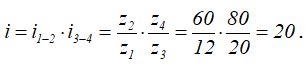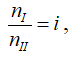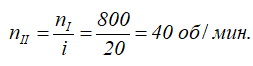Загрузить PDF
Загрузить PDF
В машиностроении передаточное отношение является показателем отношения частоты вращения двух или более сцепленных шестерен. Как правило, когда мы имеем дело с двумя шестернями, и ведущая шестерня (получающая поворачивающую силу непосредственно от двигателя) больше ведомой шестерни, то последняя вращается быстрее (и наоборот). Формула для вычисления: передаточное отношение = T2/ T1, где T1 — количество зубьев первой шестерни, Т2 — количество зубьев второй шестерни.[1]
Две шестерни
-
1
Для того чтобы определить передаточное отношение, у вас должно быть по крайней мере две шестерни, сцепленных друг с другом; такое сцепление называется зубчатой передачей. Как правило, первая шестерня является ведущей шестерней (крепится к валу двигателя), а вторая — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть сколь угодно много шестерен. Они называются промежуточными.
- Сейчас рассмотрим зубчатую передачу с двумя шестернями. Для определения передаточного отношения эти шестерни должны быть сцеплены друг с другом (то есть их зубья сцеплены и одна шестерня поворачивает другую). Например, дана небольшая ведущая шестерня (шестерня 1) и большая ведомая шестерня (шестерня 2).
-
2
Посчитайте количество зубьев на ведущей шестерне. Простейший способ найти передаточное отношение между двумя шестернями — сравнить количество зубьев на каждой из них. Начните с определения количества зубьев на ведущей шестерне. Вы можете сделать это вручную или посмотреть на маркировку шестерни.
- В нашем примере допустим, что меньшая (ведущая) шестерня имеет 20 зубьев.
-
3
Посчитайте количество зубьев на ведомой шестерне.
- В нашем примере допустим, что большая (ведомая) шестерня имеет 30 зубьев.
-
4
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В зависимости от условий задачи вы можете записать ответ в виде десятичной дроби, обыкновенной дроби или в виде отношения (х:у).
- В нашем примере: 30/20 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
- Такое передаточное отношение означает, что меньшая ведущая шестерня должна совершить полтора оборота, чтобы большая ведомая шестерня совершила один оборот. Это имеет смысл, так как ведомая шестерня больше, а значит вращается медленнее.[2]
Реклама
Более двух шестерен
-
1
Зубчатая передача может включать сколь угодно большое количество шестерен. В этом случае первая шестерня является ведущей шестерней (крепится к валу двигателя), а последняя — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть несколько промежуточных шестерен; они используются для изменения направления вращения или для сцепления двух шестерен (когда сцепление напрямую невозможно).[3]
- Рассмотрим пример, приведенный выше, но теперь ведущей шестерней станет шестерня с 7 зубьями, а шестерня с 20 зубьями превратится в промежуточную шестерню (ведомая шестерня с 30 зубьями остается той же).
-
2
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни. Помните, что при определении передаточного отношения зубчатой передачи с несколькими шестернями важно знать только количество зубьев ведомой шестерни и количество зубьев ведущей шестерни, то есть промежуточные шестерни на значение передаточного отношения не влияют.
- В нашем примере: 30/7 = 4,3. Это означает, что ведущая шестерня должна совершить 4,3 оборота, чтобы ведомая (большая) шестерня совершила один оборот.
-
3
Если необходимо, найдите передаточные отношения для промежуточных шестерен. Для этого начните с ведущей шестерни и двигайтесь в направлении ведомой шестерни. При каждом новом вычислении передаточного отношения для промежуточных шестерен рассматривайте предыдущую шестерню в качестве ведущей (и делите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни).
- В нашем примере передаточные отношения для промежуточной шестерни: 20/7 = 2,9 и 30/20 = 1,5. Заметьте, что передаточные отношения для промежуточной шестерни отличаются от передаточного отношения всей зубчатой передачи (4,3).
- Также заметьте, что (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Реклама
-
1
Определите частоту вращения ведущей шестерни. Используя передаточное отношение и частоту вращения ведущей шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (rpm).
- Рассмотрим пример зубчатой передачи, описанной выше (с тремя шестернями). Здесь частота вращения ведущей шестерни равна 130 оборотам в минуту. Вычислим частоту вращения ведомой шестерни.
-
2
Подставьте соответствующие значения в формулу: S1 × T1 = S2 × T2, где S1, Т1 — частота вращения и количество зубьев ведущей шестерни; S2, Т2 — частота вращения и количество зубьев ведомой шестерни.
- В нашем примере нужно найти S2, но по этой формуле вы можете найти любую переменную.
- 130 rpm × 7 = S2 × 30
-
3
Теперь просто обособьте неизвестную переменную на одной стороне уравнения, чтобы получить ответ. Не забудьте приписать к нему соответствующую единицу измерения.
- В нашем примере:
- 130 rpm × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30,33 rpm = S2
- Другими словами, если ведущая шестерня вращается со скоростью 130 оборотов в минуту, ведомая шестерня будет вращаться со скоростью 30,33 оборотов в минуту. Это имеет смысл, так как ведомая шестерня значительно больше, а значит вращается намного медленнее.
Реклама
Советы
- Для того, чтобы понять принцип передаточного отношения в действии, покатайтесь на велосипеде! Обратите внимание, что проще всего ехать в гору, когда у вас небольшая шестерня спереди, а большая сзади. Хотя педалями легче крутить меньшую шестерню, понадобится множество вращений, чтобы заставить заднее колесо вращаться, то есть скорость велосипеда будет ниже.
- Мощность, необходимая для движения нагрузки, может увеличиваться или уменьшаться (относительно мощности двигателя) посредством зубчатой передачи. При проектировании двигателя необходимо учитывать передаточное отношение, чтобы мощность двигателя соответствовала характеру будущей нагрузки. Повышающая система (в которой обороты вала нагрузки выше, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при меньших скоростях вращения ведущего вала.
- С другой стороны, понижающая система (в которой обороты вала нагрузки ниже, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при больших скоростях вращения ведущего вала.
Реклама
Об этой статье
Эту страницу просматривали 257 873 раза.
Была ли эта статья полезной?
Как рассчитать передаточное отношение шестерен механической передачи.
В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев. Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев.
Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.
Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.
Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.
Итак, рассмотрим пример расчета с использованием двух шестерен.
Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.
В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.
Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.
Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.
Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.
Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.
В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.
Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Определим теперь частоту вращения.
Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.
Будем использовать формулу: S1 × T1 = S2 × T2,
Где:
S1 – частота вращения желтой (ведущей) шестерни,
Т1 – количество зубьев желтой (ведущей) шестерни;
S2- частота вращения красной шестерни,
Т2 – количество зубьев красной шестерни.
В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.
340 rpm × 7 = S2 × 40
2 380 =S2 × 40
2 380 40 = S2
59,5 об/мин = S2
Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.
Целью кинематического
анализа является определение угловых
скоростей звеньев и передаточных
отношений.
Передаточное
отношение между звеньями a
и b
определяется как отношение их угловых
скоростей (или частот вращения):
.
(3.1)
Угловые скорости и
частоты вращения связаны соотношениями
;
.
Очевидно,
что перестановка индексов у величины
приводит к получению обратной величины,
т.е.
.
Если оси вращения
звеньев a
и b
параллельны, то передаточному отношению
и угловым скоростям
и
присваиваются знаки «+» или «-» по
следующим правилам:
|
|
|
|
|
Рис. 3.1 |
Рис. 3.2 |
любое
из двух возможных направлений вращения
принимают за положительное (обычно
положительным считают направление
вращения входного вала механизма), тогда
угловая скорость каждого звена
кинематической цепи приобретает вполне
определенный знак;
при
одинаковом направлении угловых скоростей,
входящих в (3.1), они имеют одинаковые
знаки и, следовательно, определяют
положительное передаточное отношение.
Очевидно,
что для пары внутреннего зацепления
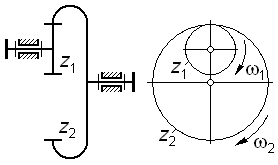
(рис. 3.1) передаточное отношение
,
(3.2)
а
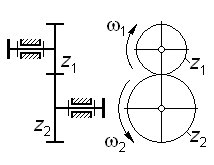
для пары внешнего зацепления (рис. 3.2) —
.
(3.3)
Кинематика рядовых
механизмов
Зубчатый
механизм, у которого все звенья вращаются
вокруг неподвижных осей, называют
рядовым.
Такой механизм может быть одноступенчатым
(рис. 3.1 и 3.2) и многоступенчатым
(рис. 3.3
и 3.4).
В многоступенчатом
рядовом механизме число ступеней
совпадает с числом зацеплений, его общее
передаточное отношение определяют как
произведение передаточных отношений
всех последовательно соединенных
ступеней.
|
|
|
|
|
Рис. 3.3 |
Рис. 3.4 |
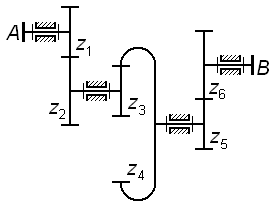
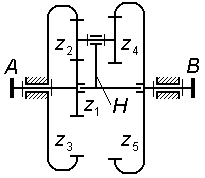
Так
для трехступенчатого механизма по рис.
3.3 общее передаточное отношение
определится по формуле
.
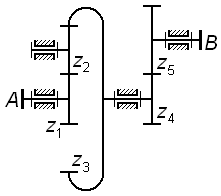
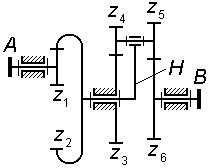
На
рис. 3.4 также представлен трехступенчатый
механизм, у которого колеса
образуют соосную кинематическую цепь
и, кроме того, колесо
участвует одновременно в двух зацеплениях
– в одном как ведомое, в другом как
ведущее (такие колеса называют связанными);
для этого механизма
.
Отметим,
что при
(выходной вал B
вращается
медленнее входного вала A)
механизм называют редуктором,
а при
— мультипликатором.
Кинематика
планетарных и дифференциальных
механизмов
Планетарные
и дифференциальные механизмы включают
в себя колеса, оси которых являются
подвижными. Рычаг, на котором расположены
эти оси, называют водилом,
а колёса с подвижными осями — сателлитами.
Ось вращения водила является центральной
осью механизма.
Колёса, которые вращаются или могут
вращаться относительно центральной
оси и при этом зацепляются с сателлитами,
называют центральными
или
солнечными.
В
планетарную ступень входят: водило;
сателлиты, размещенные на этом водиле;
колёса, которые зацепляются с этими
сателлитами.
|
|
|
Рис. 3.5 |
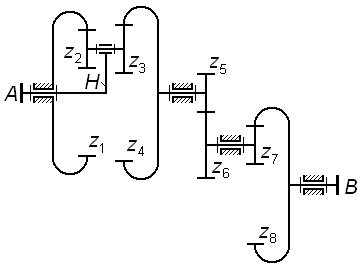
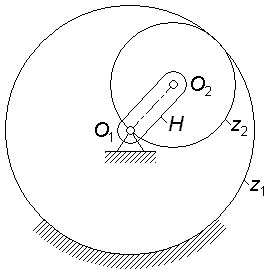
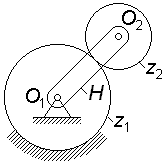
На
рис. 3.5 представлен простейший планетарный
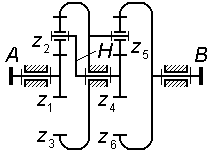
механизм, состоящий из водила H,
центрального колеса
и сателлита
.
Колесо
и водило H
вращаются относительно центральной
оси механизма.
Сателлит
совершает сложное вращательное движение,
состоящее из двух: вокруг своей
геометрической оси и одновременно,
вместе с водилом, вокруг центральной
оси механизма.
У этого механизма две
степени свободы
,
поэтому
его называют дифференциальным
механизмом, или
дифференциалом.
Кинематику такого механизма можно
описать формулой
;
(3.4)
здесь
— абсолютные угловые скорости
соответствующих звеньев (величины
алгебраические – положительные или
отрицательные),
— передаточное отношение обращенного
механизма (т.е.
такого воображаемого рядового механизма,
который получают из заданного планетарного
мысленной остановкой водила).
Из
(3.4) видно, что для кинематической
определимости этого механизма из трех
угловых скоростей две должны быть
заданы, т.е. механизм действительно
является дифференциалом.
Общий вид формулы
(3.4), пригодный для описания кинематики
практически любого планетарного
механизма, имеет вид
;
(3.5)
ее
называют формулой Р.Виллиса. Здесь a
и b
– любые два колеса одной
и той же планетарной
ступени,
— передаточное отношение от a
к b
в обращенном (рядовом) механизме, это
отношение всегда выражается через числа
зубьев колес.
Величины
угловых скоростей
и
могут быть любыми; в частности, при
(т.е. колесо b
неподвижно) отношение
и тогда формула Р.Виллиса приобретает
вид
.
(3. 6)
Формула (3.5) более
универсальна и пригодна для любого
планетарного механизма, тогда как (3.6)
можно применять только для таких
планетарных ступеней, у которых имеются
неподвижные колеса (рис. 3.6 – 3.8).
|
|
|
|
|
Рис. 3.6 |
Рис. 3.7 |
Рис. 3.8 |
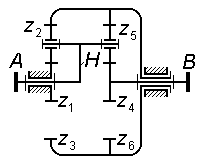
На
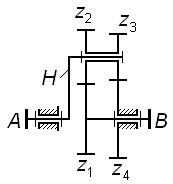
рис. 3.6 показана схема редуктора
Джемса с двухвенцовым сателлитом.
Для него
,
(3. 7)
передаточное отношение
обращенной ступени
;
(3. 
сопоставляя (3.7) и (3.8),
найдем передаточное отношение редуктора
.
(3. 9)
Таким
же способом найдем передаточное отношение
редуктора Джемса
с одновенцовым сателлитом (рис.
3.7):
,
(3.10)
;
(3. 11)
.
(3. 12)
Для
редуктора Давида
(рис. 3.8), также имеющего неподвижное
колесо в составе ступени, входным звеном
является водило H,
что отличает эту схему от двух других
при выводе формулы для
:
;
(3.13)
;
(3. 14)
.
(3. 15)
В
этих примерах показано применение
формулы Виллиса в виде (3.6), хотя было бы
вполне корректным и допустимым
использование ее в виде (3.5).
Все
схемы по рис. 3.6 – 3.8 имеют в своем составе
три центральных звена — два центральных
колеса и водило; каждое из этих звеньев
нагружено вращающим моментом либо от
источника движения, либо от потребителя
мощности (ведомого звена), либо моментом
от стойки. Такие звенья называют основными
и в соответствии с их видом и количеством
(в данном случае — два колеса и водило)
подобным схемам присвоено обозначение
типа 2KH.
|
|
|
Рис. |
На
рис. 3.9 приведена схема планетарного
механизма, содержащего четыре центральных
звена: три колеса —
,
,
и води-
ло H.
Однако водило в этой схеме не является
основным звеном, т.к. оно не может быть
нагружено никаким внешним вращающим
моментом, поэтому данный механизм
отнесен к типу 3K
(т.е. символ H
в обозначение типа механизма не входит).
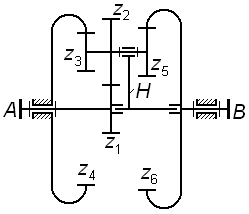
Найдем
передаточное отношение
этого механизма:
.
(3.16)
Обращенный
механизм для данной схемы представляет
собой разветвляющуюся рядовую
кинематическую цепь, каждой из двух ее
ветвей соответствует свое передаточное
отношение:
;
.
(3.17)
После очевидных
подстановок получаем
.
(3.18)
|
|
|
Рис. 3.10 |
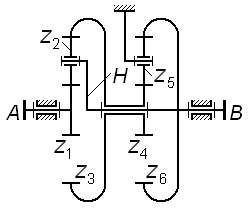
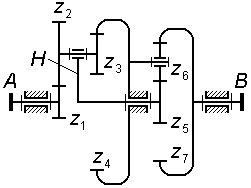
Кинематика
комбинированных механизмов с
последовательным соединением рядовых
и планетарных ступеней
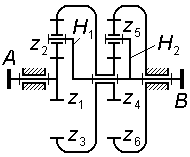
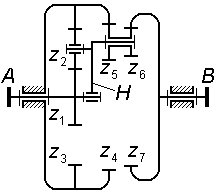
На
рис. 3.10 показан комбинированный
механизм, который
содержит:
планетарную
ступень типа 2KH
(редуктор Давида с двумя внутренними
зацеплениями), включающий в себя водило
H,
сателлиты
и
,
центральные колеса
и
;
рядовую
ступень вне-шнего зацепления
и
;
рядовую
ступень вну-треннего зацепления
и
.
Найдем
передаточное отношение механизма:
принимая во внимание, что
,
,
и
,
запишем
;
(3.19)
;
(3.20)
;
;
(3.21)
после
необходимых подстановок получаем
.
(3.22)
Как
видно из (3.19), при
последовательном соединении ступеней
общее передаточное отношение
комбинированного механизма равно
произведению передаточных отношений
всех ступеней. Единственная трудность
при анализе таких механизмов – корректно
выделить планетарные ступени и для них
написать правильные формулы передаточных
отношений.
Кинематика
замкнутых механизмов
|
|
|
Рис. 3.11 |
Проанализируем
структуру комбинированного механизма,
представленного на рис. 3.11; он включает
в себя: дифференциальную ступень (
)
и рядовую кинематическую цепь (
).
Кинематика дифференциальной
ступени описывается формулой Р.Вил-лиса
;
(3.23)
если
бы любые две из трех угловых скоростей
могли у этой ступени быть независимыми,
то данный механизм имел бы две степени
свободы. Однако, поскольку
и
,
то угловые скорости
дифференциала связаны между собой
соотношением
.
(3.24)
Таким
образом, звенья
и H
дифференциала имеют жесткую кинематическую
связь в виде рядовой цепи (
);
эта цепь как бы замыкает дифференциальную
ступень, и механизмы такого типа обычно
называют замкнутыми
дифференциалами.
Если
учесть соотношения
и
,
то (3.23) можно записать в виде
;
(3.25)
тогда
передаточное отношение механизма
.
(3.26)
Впредь
для анализа кинематики подобных
механизмов можно придерживаться такой
методики:
1)
выделить в схеме дифференциальную
ступень, содержащую водило, размещенные
на нем сателлиты и центральные колеса,
зацепляющиеся с этими сателлитами; для
выделенной ступени написать формулу
Р.Виллиса по типу (3.23), ни одна из угловых
скоростей не должна быть равна нулю
(т.е. ступень не должна содержать
неподвижных колес);
2)
выделить в схеме замыкающую кинематическую
цепь, связывающую между собой какие-то
центральные звенья дифференциальной
ступени; если эта цепь рядовая, то
написать для нее формулу по типу (3.24);
3)
написать уравнения внутренних
кинематических связей (для данного
механизма – формулы
и
);
4)
написать уравнения внешних кинематических
связей (для данного механизма — формулы
и
);
5)
используя зависимости, полученные в
пунктах 2 – 4, выразить каждую угловую
скорость, входящую в формулу Р.Виллиса
(п. 1) через
или
,
чтобы получить уравнение по типу (3.25);
из этого уравнения вывести формулу для
.
Синтез
зубчатых механизмов. Особенности синтеза
планетарных и непланетарных соосных
механизмов
Синтез
зубчатого механизма включает в себя
решение ряда задач, начиная с выбора
его кинематической схемы и заканчивая
подбором параметров этой схемы.
В
данном пособии схема механизма всегда
считается заданной и основное внимание
уделено проблемам подбора чисел зубьев
и некоторых других параметров
кинематических схем.
При
подборе чисел зубьев колес в первую
очередь стремятся обеспечить требуемую
величину передаточного отношения;
решение этой задачи синтеза почти всегда
многовариантно, поскольку связано при
заданном
с необходимостью решения неопределенных
уравнений видов (3.2), (3.3), (3.9), (3.12), (3.15),
(3.18), (3.22), (3.26) и т.д.
Введем
понятие – передаточное
число u;
оно характеризует пару зацепляющихся
друг с другом колес и его вычисляют по
формуле
;
(3.27)
здесь
— большее из чисел зубьев колес пары,
— меньшее. Таким образом, величина u
всегда положительна и она не может быть
меньше единицы.
Выбирая
из множества вариантов подбора чисел
зубьев наиболее приемлемый (с точки
зрения проектировщика), следует по
возможности
руководствоваться рекомендациями:
не
использовать колеса с числами зубьев
и
;
не
применять пары внешнего зацепления с
и пары внутреннего зацепления с
.
При
подборе чисел зубьев колес планетарных,
дифференциальных, а также рядовых
соосных кинематических цепей (как,
например, часть механизма, состоящая
из колес (
)
на рис. 3.4), необходимо принимать во
внимание еще некоторые специфические
требования.
Условие
соосности. Это
условие выражает факт равенства межосевых
расстояний в зацеплениях центральных
колес и сателлитов. Например, для схемы
по рис. 3.4 должно соблюдаться равенство
,
которое можно привести к виду
;
(3.28)
для
схемы по рис. 3.6 аналогичное условие
выглядит как
,
или
;
(3.29)
в
равенствах типа (3.28) и (3.29) участвуют
суммы (для пар внешнего зацепления) или
разности чисел зубьев колес (для пар
внутреннего зацепления).
|
|
|
Рис. 3.12 |
Условие
соседства.
Планетарные механизмы редко выполняют
с одним сателлитом; обычно их ставят
два или более, что позволяет разделить
передаваемую мощность на несколько
параллельных потоков в соответствии с
числом сателли-тов
.
При
многосателлитном исполнении механизма
соседние сателлиты не должны касаться
друг друга вершинами зубьев; это
требование выполняется, если расстояние
между осями соседних сателлитов больше
их диаметра вершин. Так, для варианта
схемы по рис. 3.12 должно соблюдаться
неравенство
.
В
общем виде это условие можно записать
так
;
(3.30)
здесь
— межосевое расстояние в зацеплении
центральных колес и сателлитов («радиус»
водила);
—
наибольший из диаметров вершин соосных
сателлитов, принадлежащих одной
планетарной ступени.
Неравенству
(3.30) обычно придают вид, которым удобнее
пользоваться, когда диаметральные
размеры колес еще неизвестны:
;
(3.31)
здесь
— наибольшее из чисел зубьев соосных
сателлитов, принадлежащих данной
планетарной ступени;
—
сумма или разность чисел зубьев,
участвующих в условии соосности.
Для схемы по рис. 3.6
условие (3.31) имеет вид
(3.32)
(у
такого механизма всегда
).
Условие
сборки. Сборка
механизма с одним сателлитом (
)
осуществима всегда, если числа зубьев
колес удовлетворяют условию соосности.
Если
,
то при установке на водиле второго и
последующих сателлитов их зубья должны
быть введены во впадины одновременно
двух центральных колес; это выполнимо
далеко
не всегда.
Как
показывает анализ, сборка многосателлитного
планетарного механизма осуществима
тогда и только тогда, когда числа зубьев
его колес и количество сателлитов
удовлетворяют так называемому условию
сборки (или
сцепляемости). Это условие всегда
записывается в виде некоторого выражения:
сборка механизма возможна только в том
случае, если значение этого выражения
целочисленно.
Рассмотрим
способ формирования выражения для
проверки собираемости планетарной
многосателлитной ступени. Пусть
передаточное отношение обращенного
механизма имеет вид
;
(3.33)
здесь
M
и N
– числитель и знаменатель выражения
для
;
отметим, что
— величина алгебраическая, т.е. положительная
или отрицательная. Вид выражения для
условия сборки полностью определяется
строением (3.33) и здесь встречаются два
случая.
Если
выражение (3.33) записано для той части
механизма, в которой сателлит является
связанным колесом (в таком случае его
число зубьев отсутствует в этом
выражении), то условие сборки для
соответствующей части механизма имеет
вид
;
(3.34)
здесь
— знак «+» или «-», всегда противоположный
знаку величины
;
Ц
– любая целая величина.
Если
у той части механизма, для которой
записана формула (3.33), сателлит двухвенцовый
(числа зубьев обоих венцов обязательно
присутствуют в этой формуле), то условие
сборки принимает вид
;
(3.35)
здесь
и Ц
имеют тот же смысл, что и в (3.34); B
– общий наибольший делитель чисел
зубьев венцов сателлитов, участвующих
в
записи (3.33) (обычно величина B
имеет индексы, указывающие на номера
этих венцов в кинематической схеме).
Рассмотрим
в качестве примеров взаимосвязь формул
для передаточного отношения обращенного
механизма и соответствующих условий
сборки для некоторых кинематических
схем, приведенных выше.
Табл. 3.1
|
Номер рисунка |
Формула передаточного обращенного |
Номера зубчатых венцов сателлитов |
Формулы условий |
|
Рис. 3.6 |
|
|
|
|
Рис. 3.7 |
|
|
|
|
Рис. 3.8 |
|
|
|
|
Рис. 3.9 |
|
||
|
|
|
|
|
|
Рис. 3.10 |
|
|
Обращенный
механизм для редуктора 3К (рис. 3.9)
представляет собой разветвляющуюся
кинематическую цепь; для каждой из двух
ветвей записывается своя формула
передаточного отношения и свое условие
сборки.
В
заключение добавим, что обращенный
механизм является по определению рядовым
и притом соосным механизмом; поэтому
все описанные особенности синтеза
планетарных механизмов без каких-либо
оговорок и ограничений распространяются
на рядовые соосные механизмы.
|
Задача
Сколько неподвижно, соотношение чисел зубьев |
|
|
Задача
Сколько совершит один оборот; колесо неподвижно, соотношение чисел зубьев . |
|
|
Задача
Определить
если . |
|
|
Задача
Сколько относительно водила H, неподвижно, соотношение чисел зубьев . |
|
|
Задача
Определить
если |
|
|
Задача
Сколько совершит один оборот; колесо неподвижно, соотношение чисел зубьев . |
|
|
Задача
Сколько , неподвижно, соотношение чисел зубьев . |
|
|
Задача
Сколько относительно водила H, неподвижно, соотношение чисел зубьев . |
|
|
Задача
Найти
Соотношение . |
|
|
|
Задача
Для |
|
Задача
Для , |
|
|
Задача
Для |
|
|
Задача
Для , |
||
|
|
Задача
Для |
|
|
Задача
Для , при |
||
|
Задача
Для |
||
|
Задача
Считая, найти частоту относительного вращения |
|
|
|
|
Задача
Считая, найти частоту относительного вращения , |
|
|
Задача
Формулу передаточного
редуктора |
|
|
|
Задача
Для |
||
|
|
Задача
Для , |
|
|
Задача
Для |
|
|
|
|
Задача
Для
Рассчитать при
|
|
|
Задачи
Формулу |
||
|
К задаче 3.24
|
К задаче 3.25
|
К задаче 3.26
|
|
|
Задача
Для , |
|
|
Задача
Для при |
|
Задача
|
Вал
Найти относительно водила H, |
|
Задача
Вал относительно вала водила H, . |
|
|
Задача
|
Вал = 25; найти относительно вала A, |
|
Задача
Вал , = 25; найти относительно вала A, . |
|
|
Задача |
Вал , = 25; найти относительно вала A, . |
|
Задача
Выходной и относительно вала водила, если |
|
|
Задача
|
Выходной , = 31; и относительно входного вала, если . |
|
Задача
Передаточное |
|
|
Задача
Вал относительно вала A, |
|
|
Задача
Вал , . относительно водила H, |
|
|
Задача
|
Выходной . |
|
Задача
Входной ; |
|
|
Задача
Определить относительно вала A, и передаточное отношение редуктора .
Выходной |
|
|
Задача
|
Определить относительно вала водила и частота вращения выходного вала |
|
Задача
Частота |
|
|
Задача
|
Частота |
|
Задача
Передаточное
выразить через числа |
|
|
Задача
Рассчитать редуктора при следующих соотношениях |
|
Задача 3.46
Водило неподвижно.
Определить и |
|
|
Задача
|
Рассчитать редуктора, если числа зубьев колес . |
|
Задача
Подобрать и редуктора, обеспечивающих получение |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи по определению угловой скорости шестерни ведомого вала редуктора по заданной угловой скорости колеса ведущего вала и передаточному числу
Задача
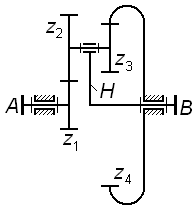
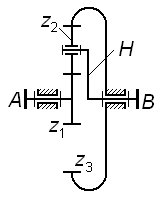
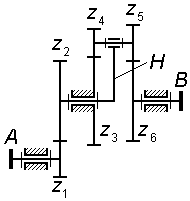
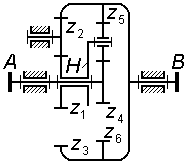
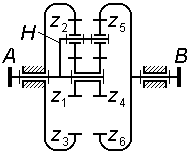
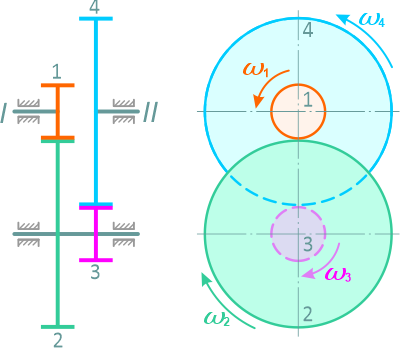
Редуктор обеспечивает вращение валов I и II, имеющих общую геометрическую ось, с различными угловыми скоростями (рисунок 1.10).
Рис. 1.10
Определить угловую скорость вала II, соответствующую угловой скорости вала I, равной n1=800 об/мин, если числа зубьев шестерен соответственно равны: z1=12, z2=60, z3=20, z4=80.
Другие примеры решений >
Помощь с решением задач >
Решение
Передаточное число редуктора равно отношению угловой скорости ведущего вала к угловой скорости ведомого:
При этом угловые скорости ведущего и ведомого валов равны угловым скоростям жестко соединенных с ними шестерен:
ωI = ω1, ωII = ω4.
Для получения зависимости между угловыми скоростями шестерен 1 и 4 следует определить передаточное число передачи, состоящей из двух пар колес:
Пользуясь угловыми скоростями, выраженными в об/мин, имеем:
откуда
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Расчет зубчатой передачи
Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).
Назначение. Зубчатые передачи относятся к механическим передачам зацепления с непосредственным контактом и применяются для изменения скорости или направления вращения ведомого звена с соответствующим изменением крутящего момента, получения точных перемещений, при необходимости точного соответствия скоростей и положений ведущего и ведомого звеньев в произвольный момент времени. Зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее — колесом. Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными, пересекающимися и перекрещивающимися осями.
|
|
|
|
|
|
а |
б |
в |
г |
|
|
|
|
|
|
д |
е |
ж |
з |
|
|
|
|
|
|
и |
к |
л |
м |
Рис. 81. Виды зубчатых передач: а – внешнего зацепления прямозубая, б – внешнего зацепления косозубая, в – внутреннего зацепления прямозубая, г – внешнего зацепления реечная, д – внешнего зацепления шевронная, е – коническая прямозубая, ж – коническая косозубая, з – коническая круговая, и – коническая круговая — гипоидная, к – внешнего зацепления винтовая, л – передача с круговыми зубьями, м — планетарная.
Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.
Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.
Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают 10, а для закрытой
25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать
0,99.
Геометрический расчет. Передаточное отношение передачи
, (14.1)
где — число зубьев шестерни и колеса соответственно.
Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:
1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.
2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.
При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.
Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:
, (14.2)
где и
— начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус — к передаче с внутренним зацеплением.
Стандартизированы номинальные значения межосевых расстояний aw, мм:
1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800
2-й ряд — — 71; 98; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900.
Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:
. (14.3)
Делительные диаметры для зубчатых колес прямозубой передачи
d = zm, (14.4)
для косозубой и шевронной
. (14.5)
где т — модуль зацепления основная характеристика размеров зубчатых и червячных колес. Для обеспечения взаимозаменяемости и унификации инструмента для изготовления модули цилиндрические и конические эвольвентных зубчатых колес стандартизованы: для цилиндрических колес — значения нормальных модулей, для конических — значения окружных делительных модулей в диапазоне 0,05..100мм.
1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;
2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.
Ширина венца цилиндрического зубчатого колеса определяется по одной из формул
, (14.6)
или
, (14.7)
где — коэффициент ширины зубчатого венца по межосевому расстоянию, а
— коэффициент ширины зубчатого венца по диаметру шестерни.
Коэффициенты и
связаны зависимостью:
. (14.8)
Значения коэффициентов ширины венца зубчатых колес по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.
Рис. 82. Обозначения элементов зубчатого зацепления.
Для заданного числа зубьев и
, коэффициентов смещения исходного контура
и
, угла наклона зубьев
основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:
|
Параметр |
Шестерня |
Колесо |
|
Делительный диаметр |
|
|
|
Основной диаметр |
|
|
|
Начальный диаметр |
|
|
|
Диаметр вершин зубьев |
|
|
|
Диаметр впадин зубьев |
|
|
|
Межосевое расстояние |
|
|
|
Делительный угол профиля в торцевом сечении |
|
|
|
Коэффициент торцевого перекрытия |
|
|
|
Рабочая ширина зубчатого венца |
|
|
|
Коэффициент осевого перекрытия (при ширине венца |
|
|
|
Основной угол наклона |
|
Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:
— шестерни ; (14.9)
— колеса ,
где — угловая скорость зубчатого колеса; п — частота вращения зубчатого колеса;
— начальный диаметр цилиндрического зубчатого колеса.
Окружная сила цилиндрической зубчатой передачи Ft

где — крутящий момент на шестерне.
Сила давления между зубьями в цилиндрической прямозубой передаче
. (14.11)

, и радиальная сила
, в конической прямозубой и цилиндрической косозубой передачах — окружная сила
, радиальная сила
, и осевая сила Fa.
Радиальная сила в цилиндрической передаче
, (14.12)
Осевая сила, действующая на колесо косозубой цилиндрической передачи
, (14.13)
Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности () размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.
Проектные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние

где — коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430,
— момент на зубчатом колесе передачи в
,
— коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84;
— допускаемое контактное напряжение в МПа.
Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на контактную прочность.
Коэффициент ширины венца по межосевому расстоянию для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении
= 0,315…0,4; для зубчатых колес из закаленных сталей
= 0,25…0,315; при симметричном расположении зубчатых колес относительно опор
= 0,4…0,5; для передвижных зубчатых колес коробок скоростей
= 0,1…0,2. Принимаются стандартные значения
.
Допускаемое контактное напряжение
, (14.15)
где — предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1);
— коэффициент безопасности; ZR — коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv — коэффициент, учитывающий окружную скорость передачи; KHL — коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9…1; ZR =1,0 при
мкм, ZR =0,95 при
мкм и ZR =0,9 при
мкм. Коэффициент Zv = 1…1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v << 5м/с Zv = 1. При приближенном расчете можно принимать
.
Коэффициент долговечности KHL определяют в зависимости от отношения — базового числа циклов нагружения при котором определяется предел контактной выносливости и
— эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают в зависимости от твердости НВ рабочей поверхности зубьев либо по формуле
. (14.16)
При эквивалентном числе циклов нагужения зубьев колес больше базового коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов
нагружения зубьев меньше базового то

Если при расчете колес из нормализованной или улучшенной стали , то принимают
.
Таблица 14.1. Предел контактной выносливости при базовом числе циклов
|
Термическая обработка |
Твердость поверхностей зубьев |
|
|
Нормализация или улучшение |
|
|
|
Объемная закалка |
|
|
|
Поверхностная закалка |
|
|
|
Цементация или нитроцементация |
|
|
|
Азотирование |
|
|
Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой
, (14.18)
где с — число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; — частота вращения рассчитываемого зубчатого колеса,
; t — продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
, (14.19)
где Tmax — максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; — передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения
.
Допускаемое контактное напряжение для зубьев прямозубых передач определяют раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых передач, в которых зубья шестерни значительно превышают твердость зубьев колеса, расчетное контактное напряжение
, (14.20)
где и
— допускаемые контактные напряжения зубьев шестерни и колеса, вычисляемые по формуле (14.15);
— минимальное допускаемое напряжение из этих двух допускаемых напряжений.
Полученный по формуле (14.14) межосевое расстояние следует округлить до ближайшего большего стандартного значения. При проектировочном расчете числом зубьев
шестерни задаются, а число зубьев колеса
. Для зубчатых передач без смещения рекомендуется принимать
зубьев для обеспечения отсутствия подрезание зубьев. Для уменьшения габаритных размеров тихоходных зубчатых передач допускается
зубьев. В быстроходных передачах в целях уменьшения шума рекомендуется принимать
зубьев.
Расчет зубьев на изгибную прочность. Предварительное значение модуля зубчатой передачи определяется из условия проектного расчета зубьев на изгиб.

Рис. 85. Коэффициент формы зуба.
где — коэффициент для прямозубых передач
=14, для косозубых и шевронных
=11,2;
— коэффициентом формы зуба, который определяется по рис.85;
— коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, который определяется по рис.86;
— момент на шестерне передачи в
,
— число зубьев шестерни; а
— коэффициент ширины зубчатого венца по диаметру шестерни, который определяется по формуле (14.8),
допускаемые напряжения при изгибе зубьев.
Для косых зубьев коэффициент YF определяют не по действительному числу зубьев z, а по эквивалентному по зависимости
. (14.22)
Допускаемое напряжение на изгиб для зубьев
, (14.23)
где — предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений (табл.14.2);
— коэффициент безопасности зубьев на изгиб;
— коэффициент долговечности зубьев на изгиб;
— коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья;
; коэффициент безопасности
=1,7…2,2 (большие значения для литых заготовок).
Рис. 86. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на изгибную прочность. Схемы расположения колес показаны на рис.84.
Таблица 14.2 Пределы выносливости материалов зубчатых колес на изгиб
|
Вид термообработки и марка стали |
Твердость зубьев |
|
|
|
на поверхности |
в сердцевине |
||
|
Цементация легированных сталей: |
|||
|
содержание Ni более 1% Cr 1% и менее (например, 20ХН2М, 12ХН2, 12ХН3А) |
57-63 |
32-45 |
950 |
|
стали марок 18ХГТ, 30ХГТ, 12Х2Н4А и др. |
57-63 |
32-45 |
800 |
|
Нитроцементация легированных сталей: |
|||
|
25ХГМ |
57-63 |
32-45 |
1000 |
|
25ХГТ, 30ХГТ и др. |
57-63 |
32-45 |
750 |
|
Заделка при нагреве ТВЧ по всему контуру: |
|||
|
стали пониженной прокаливаемости (например, 55ПП) |
58-62 |
28-35 |
900 |
|
стали марок 60ХВ, 60ХН и др. |
54-60 |
25-35 |
700 |
|
стали марок 35ХМА, 40ХН и др. |
48-60 |
25-35 |
600 |
|
Нормализация или улучшение |
НВ |
180-350 |
1,35НВ+100 |
|
Азотирование легированных сталей |
— |
24-40 |
18HRCсерд+50 |
Коэффициент долговечности определяют в зависимости от отношения
— базового числа циклов нагружения при котором определяется предел контактной выносливости и
— эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. При эквивалентном числе циклов нагружения зубьев колес больше базового
коэффициент долговечности
=1.
В случае когда эквивалентное число циклов нагружения зубьев меньше базового, то

Для зубчатых колес с твердостью поверхности зубьев , а также со шлифованной переходной поверхностью зубьев показатель корня т=6, для зубчатых колес с
и нешлифованной переходной поверхностью т=9. Базовое число циклов нагружений зубьев изгибом
.
Эквивалентное число циклов перемены напряжений NFE. при работе передачи с постоянной нагрузкой
, (14.25)
где с — число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; — частота вращения рассчитываемого зубчатого колеса,
; t — продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
, (14.26)
где Tmax — максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; — передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения , показатель степени принимается согласно рекомендациям к формуле (14.24).
Значение коэффициента принимают: при односторонней нагрузке на зубья
, а при двусторонней
= 0,7…0,8 (большее значение при НВ > 350).
При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости
, (14.27)
где — коэффициент для прямозубой передачи
=1400, для косозубой и шевронной
=850.
Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния и модуля
определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.
Проверочные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
— для прямозубых передач

— для косозубых передач

где ,
— коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления;
— коэффициент динамической нагрузки, возникающей в зацеплении.
Таблица 14.3 Значения коэффициента динамических нагрузок
|
Степень точности |
Твердость поверхностей зубьев |
υ, м/с |
|||||
|
1 |
2 |
4 |
6 |
8 |
10 |
||
|
6-я |
а |
||||||
|
б |
|||||||
|
7-я |
а |
||||||
|
б |
|||||||
|
8-я |
а |
||||||
|
б |
|||||||
|
9-я |
а |
||||||
|
б |
Примечания: 1. Твердость поверхности зубьев: а) и
или
и
; б)
и
. 2. 3начения
в числителе относятся к прямозубым передачам, а в знаменателе — к косозубым.
Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а — для расчета на контактную прочность, b – для расчета на изгибную прочность.
Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент определяются по графикам на рис.87. Коэффициент динамической нагрузки
определяют по таблице 14.3.
Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями : а — для расчета на контактную прочность, b – для расчета на изгибную прочность.
При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:

где — максимальное расчетное напряжение при перегрузке зубьев максимальным моментом
;
— допускаемое максимальное контактное напряжение для зубьев;
— расчетное контактное напряжение, вызываемое расчетным моментом
и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском
, где
— предел текучести материала зубьев при растяжении; для зубьев с термообработкой — цементация, контурная закалка после нагрева ТВЧ —
; для азотированных зубьев
. Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.
Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
, (14.31)
где — коэффициент учитывающий перекрытие зубьев;
— коэффициент наклона зубьев;
— коэффициент распределения нагрузки между зубьями;
— коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи,
— коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.
При подстановке окружной силы по зависимости (14.10) формула (14.31) преобразуется к виду
.
Коэффициент, учитывающий перекрытие зубьев
.
При приближенных расчетах для для косозубых передач и прямозубых передач принимают .
Коэффициент наклона зубьев для прямозубых передач , для косозубых определяется по зависимости
, (14.32)
при
.
Коэффициент неравномерности распределения нагрузки для прямозубых передач принят , а для косозубых коэффициент
определяются по графикам на рис.87. Коэффициент динамической нагрузки
определяют по таблице 14.4
Таблица 14.4 Значения коэффициента динамических нагрузок
|
Степень точности |
Твердость поверхностей зубьев |
υ, м/с |
|||||
|
1 |
2 |
4 |
6 |
8 |
10 |
||
|
6-я |
а |
||||||
|
б |
|||||||
|
7-я |
а |
|
|||||
|
б |
|||||||
|
8-я |
а |
||||||
|
б |
|||||||
|
9-я |
а |
||||||
|
б |
Примечания: 1. Твердость поверхности зубьев: а) и
или
и
; б)
и
. 2. 3начения
в числителе относятся к прямозубым передачам, а в знаменателе — к косозубым.
Если материал зубчатых колес одинаковый, то расчет зубьев на изгиб производят по шестерне, у которой толщина зубьев у основания меньше и соответственно коэффициент формы зубьев YF больше, чем у зубьев колеса. Если материал зубьев шестерни более прочный по сравнению с материалом зубьев колеса, что обычно и принимается, то расчет зубьев на изгиб нужно производить по тому зубчатому колесу, для которого отношение имеет меньшее значение. Рекомендуется материал зубьев шестерни и колеса принимать таким, чтобы отношение
для обоих зубчатых колес было примерно одинаковым.
Если известно напряжение изгиба для зуба шестерни, то для зуба колеса условие прочности на изгиб запишется в виде
. (14.33)
При действии кратковременных перегрузок зубья проверяют на пластическую деформацию или хрупкий излом при изгибе от максимальной нагрузки:
, (14.34)
где — максимальное расчетное напряжение на изгиб в зубьях при их перегрузке максимальным моментом
;
— допускаемое максимальное напряжение на изгиб для зубьев;
— расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом
и определяемое по формуле (14.31).
Значение допускаемых максимальных напряжений
на изгиб для зубьев принимают: при твердости поверхности зубьев
, где
— предел текучести материала зубьев при растяжении; при твердости
, где
— предел прочности материала зубьев при растяжении. Расчет зубьев по формуле (14.34) производят для менее прочного колеса передачи.
Задача 14.1. Выполнить расчет зубчатой передачи. Выполнить проектный и проверочный расчеты (на контактную и изгибную прочность) косозубой зубчатой передачи быстроходной ступени двухступенчатого цилиндрического редуктора. Параметры циклограммы нагружения шестерни: момент на шестерне , продолжительность работы
;
,
;
,
. Частота вращения шестерни
. Передаточное число
, передача нереверсивная. Марка стали колес — сталь 40ХН. Способ упрочнения — закалка при нагреве ТВЧ до твердости поверхности зубьев
.
Решение. Проектный расчет зубчатой передачи.
Принимаем коэффициент ширины по межосевому расстоянию из стандартного ряда значений .
Коэффициент ширины по диаметру шестерни по формуле (14.8)
.
Ориентировочное значение коэффициента неравномерности распределения нагрузки определяем по рис.84. Твердость зубьев
соответствует твердости
, согласно зависимостям на рис.88. Для схемы ІІ, при твердости зубьев
(рис.84.):
.
Предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений определяем по таблице 14.1.
=
Рис.88. Зависимости для определения твердости в единицах
Коэффициент запаса прочности .
Базовое число нагружений для материала шестерни и колеса по формуле (14.16)
Эквивалентное число циклов нагружений зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.19) с учетом того, что частота вращения на всех режимах одинакова и равна . (При постоянном нагружении эквивалентное число циклов определяется по зависимости (14.18))
=
==
= циклов.
Эквивалентное число нагружений зубьев колеса
циклов.
Коэффициенты долговечности для зубьев шестерни и колеса по формуле (14.17)


Допустимые контактные напряжения по формуле (14.15), с учетом
— для шестерни
;
— для колеса
.
Так как твердость поверхности зубьев шестерни и колеса одинаковы, то в качестве расчетного допускаемого контактного напряжения принимаем меньшее значение
.
Расчетное межосевое расстояние определяем по формуле (14.14) для косозубой передачи

Принимаем наибольшее значение из стандартного ряда .
Находим предел усталости зубьев при изгибе по табл. 14.2. для стали 40ХН с упрочнением ТВЧ .
Базовое число циклов нагружений зубьев изгибом .
Эквивалентное число циклов нагружений изгибом зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.26) с учетом (14.24) и того, что частота вращения на всех режимах одинакова и равна :
=
=
= циклов.
Для зубьев колеса эквивалентное число циклов нагружений изгибом
циклов.
Коэффициенты долговечности для зубьев шестерни и колеса на изгиб с учетом того, что и
, то
.
Допускаемое напряжение на изгиб для зубьев шестерни определим по формуле (14.23) при и
.
Предварительно принимаем коэффициент формы зуба шестерни .
Расчетная ширина венца зубчатого колеса
.
Принимаем стандартный размер ширина венца .
Ширина зубчатого венца шестерни .
Принимаем .
По известному значению межосевого расстояния ориентировочно определяем модуль зацепления по зависимости (14.27) для косозубой передачи
мм.
Принимаем стандартное значение модуля зацепления мм.
Предварительное значение угла наклона зубьев принимаем из диапазона . Принимаем
.
Число зубьев шестерни по межосевому расстоянию и модулю определим по зависимости:
.
Принимаем число зубьев шестерни .
Число зубьев колеса
.
Уточнение угла наклона зубьев по межосевому расстоянию и числу зубьев
0,96 и
.
Принимаем коэффициент коррекции при изготовлении зубьев .
Расчет геометрических, кинематических и силовых параметров для выполнения проверочных расчетов.
Делительные диаметры колес зацепления:
— шестерни 166,67мм;
— колеса 333,33мм.
Начальные диаметры:
— шестерни 166,67мм;
— колеса 333,33мм.
Диаметр вершин зубьев:
— шестерни 176,67мм,
— колеса 343,33мм.
Диаметр впадин зубьев:
— шестерни 154,17мм,
— колеса 320,83мм.
Делительный угол профиля зуба в торцевом сечении


Угол зацепления передачи при
.
Коэффициент торцевого перекрытия:

=1,66.
Коэффициент осевого перекрытия
=
1,12.
Окружная скорость
Принимаем при такой скорости 8-ую степень точности (табл.14.5) с шероховатостью поверхности зубьев мкм.
Таблица 14.5 Степени точности зубчатых передач
|
Степень точности |
Окружная скорость колес, м/с, не более |
Область применения |
|
|
прямозубых |
косозубых |
||
|
6 — я |
15 |
30 |
Скоростные передачи, делительные механизмы |
|
7 — я |
10 |
15 |
Передачи при повышенных скоростях и умеренных нагрузках или наоборот |
|
8 — я |
6 |
10 |
Передачи общего машиностроения, не требующие особой точности |
|
9 — я |
2 |
4 |
Тихоходные передачи с пониженными требованиями к точности |
Проверочные расчеты зубчатого зацепления на контактную прочность зубьев.
Определяем по графику на рис.87. а коэффициент неравномерности распределения нагрузки в зависимости от скорости и 8-ой степени точности изготовления
Определяем по таблице 14.3 коэффициент динамической нагрузки для твердости поверхности зубьев
при скорости
и 8-ой степени точности изготовления
=1,045.
Коэффициент неравномерности
1,26.
Расчет зубьев на контактную прочность выполняем по зависимости (14.29)
Следовательно, условие контактной прочности зубьев выполнено. Допускается превышение над
до 5%.
Проверочный расчет на изгибную прочность зубьев. Определяем по графику на рис.87 а коэффициент неравномерности распределения нагрузки на изгиб в зависимости от скорости и 8-ой степени точности изготовления
.
Определяем по графику на рис.86 б коэффициент неравномерности распределения по длине контактных линий на изгиб в зависимости от схемы зацепления и твердости зубьев
.
Определяем по таблице 14.3 коэффициент динамической нагрузки на изгиб для твердости поверхности зубьев
при скорости
и 8-ой степени точности изготовления
=1,07.
Эквивалентное число зубьев косозубой передачи определяем по формуле (14.22)
— для шестерни ,
— для колеса .
Коэффициент формы зубьев колес принимаем по графику рис.85. в зависимости от эквивалентного числа зубьев:
— для шестерни 3,75,
— для колеса 3,62.
Коэффициент учитывающий угол наклона зубьев определяем по формуле (14.32)
=
=0,88.
Коэффициент, учитывающий перекрытие зубьев передачи
=
0,6.
Окружную силу в зацеплении определим по формуле (14.10)
=
25200Н.
Расчетные напряжения изгиба в зубьях
— для шестерни
,
— для колеса
.
Следовательно, условие прочности зубьев на изгиб обеспечивается.
Задача 14.2. Определить размеры открытой конической зубчатой передачи. Передаваемая мощность N=3,5·103Вт. Передаточное числа i = 4.Частота вращения ведущего вала Передача нереверсивная.
Решение. Углы при вершинах начальных конусов
Выбираем материал зубчатых колес. Материал шестерни – сталь Ст.5, материал колеса – чугун СЧ 21–40 т. к. передача открытая расчет будет производится только из условия прочности зубьев на изгиб.
Допускаемые напряжения изгиба для шестерни
где ;
для колеса
где — предел прочности чугуна СЧ 21-40 на растяжение.
Задаемся числом зубьев шестерни Тогда
Сравнительная прочность зубьев шестерни и колеса на изгиб:
для шестерни
для колеса
Таким образом, расчет следует вести по колесу.
Задаемся:
Расчетный момент на ведущем валу
Здесь принято предварительно K=1,5.
Момент расчетный на ведомом валу (валу колеса) без учета потерь в зацеплении и подшипниках
Максимальный модуль зацепления при коэффициенте износа γ = 1,2
Принимаем из ряда стандартных значений модулей (по ГОСТ 9563-80).
По найденному определяем размеры колес:
Углы конусов выступов
Тогда
.
Длина зуба
Средний модуль