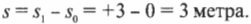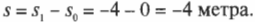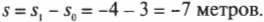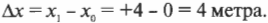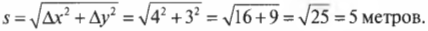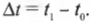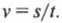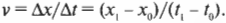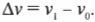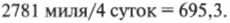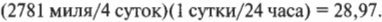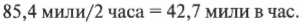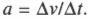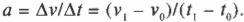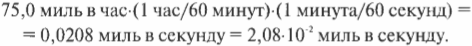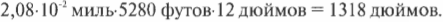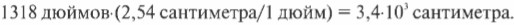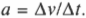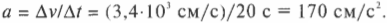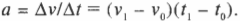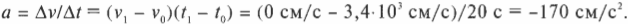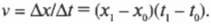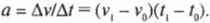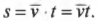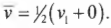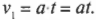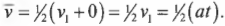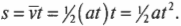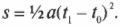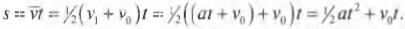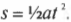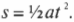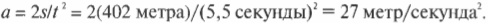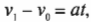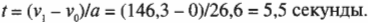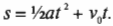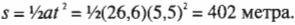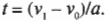to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
- Прямолинейное равномерное движение на координатной прямой
- Уравнение прямолинейного равномерного движения
- Удобная система отсчета для решения задачи о прямолинейном движении
- График движения x=x(t)
- Как найти уравнение движения по графику движения?
- График скорости vx=vx(t)
- Как найти путь и перемещение по графику скорости?
- Задачи
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin{gather*} x=x_0+s=x_0+vt\ x=20+10t end{gather*}
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:
- если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)
В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) — координата в начальный момент времени, (v_x) — проекция вектора скорости движения.
Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:
- если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
 |
Построим графики зависимости координаты от времени для нашего примера:
x=20+10t — машина движется вправо (в направлении оси OX) |
п.5. Как найти уравнение движения по графику движения?
Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$
п.6. График скорости vx=vx(t)
В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Содержание:
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
Определение и формула скорости
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:
$$v=frac{d s}{d t}=dot{s}(2)$$
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$
Следовательно, вектор скоростив декартовых координатах можно представить:
$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$
где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$
в сферической системе координат:
$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:
$$v=frac{s}{t}(8)$$
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$
где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
$$bar{v}=bar{v}_{0}+bar{a} t$$
где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с2
В СГС: [v]=см/с2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:
$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорость материальной точки является функцией от времени вида:
$$v=10left(1-frac{t}{5}right)$$
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
$$x=10 cdot 10-(10)^{2}=0(m)$$
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
$$10 t-t^{2}=-10(2.3)$$
При решении уравнения (2.3) нам подойдет корень равный:
$$t_{3}=5+6=11 (c)$$
Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$
Читать дальше: Формула средней скорости.
В этой главе. . .
- Изучаем скорость перемещения
- Разбираемся с разными видами скорости
- Замедляемся и разгоняемся
- Исследуем связь между ускорением, временем и перемещением
- Связываем скорость, ускорение и перемещение
Представьте себе, что вы участвуете в гонке “ Формула-1” и в гоночном автомобиле мчитесь навстречу славе. Скорость огромна, ветер свистит, а уверенность в победе высока, ведь отрыв от соперников значителен и осталось пройти последний поворот. Похоже, что ближайший преследователь, чемпион прошлого года, также прилагает значительные усилия — в зеркале заднего вида на мгновение показалась серебристая обшивка его болида. Необходимо что-то предпринять, поскольку преследователь очень быстро сокращает отставание.
Вам известно все или почти все о скорости и ускорении. С такими знаниями вы знаете, что нужно делать: жмете на педаль газа, и болид ускоряется. Знание законов изменения скорости позволило с легкостью пройти последний поворот. А вот и взмах клетчатого флага на финише, к которому вы пришли за рекордное время. Отлично! Безусловно, вам помогло знание именно тех тем, которые излагаются в этой главе: перемещение, скорость и ускорение.
Наверняка у вас уже есть интуитивное представление об этих понятиях, иначе вы не смогли бы управлять автомобилем или даже велосипедом. Перемещение описывает изменение места расположения, скорость характеризует быстроту перемещения, а ускорение знакомо всякому, кому приходилось перемещаться в автомобиле. С этими понятиями люди сталкиваются ежедневно, а физика поможет организовать их изучение. Знание этих физических понятий позволяет планировать дороги и транспортные развязки, строить и запускать космические корабли, отслеживать движение планет, предсказывать погоду, а также… приводит нас в бешенство в дорожной пробке.
Понимание законов физики включает понимание основ движения, и именно этой теме посвящена данная глава. Приступаем.
Содержание
- Передвигаемся и перемещаемся
- Разбираемся с осями
- Измеряем скорость
- Подробнее о скорости: что же это такое
- Смотрим на спидометр: мгновенная скорость
- Движемся постоянно: равномерная скорость
- Движемся вперед и назад: неравномерное движение
- Жмем на секундомер и определяем среднюю скорость
- Средняя скорость и неравномерное движение
- Ускоряемся и замедляемся
- Определяем ускорение
- Определяем единицу ускорения
- Положительное и отрицательное ускорение
- Среднее и мгновенное ускорение
- Равномерное и неравномерное ускорение
- Связываем ускорение, время и перемещение
- Не такие уж и далекие связи
- Выводим более сложные соотношения
- Связываем скорость, ускорение и перемещение
Передвигаемся и перемещаемся
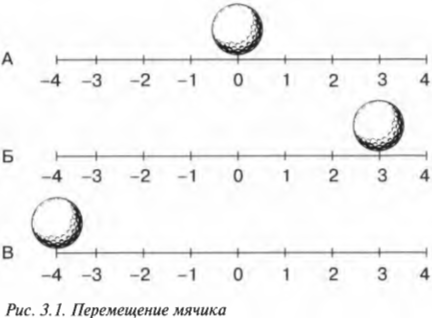
С точки зрения физики перемещение возникает при переходе какого-то объекта из точки 1 в точку 2. Попросту говоря, перемещение — это пройденное объектом расстояние. Рассмотрим, например, движущийся вдоль линейки мячик для игры в гольф, который показан на рис. 3.1. Допустим, что сначала мячик находится возле отметки 0 (схема А).
Пока что все в порядке. Допустим, что мячик сместился на новое место, например на 3 метра вправо (схема Б). В таком случае говорят, что мячик переместился, или произошло перемещение. В данном случае перемещение равно 3 метрам. В исходном положении мячик находился на отметке 0 метров, а в конечном положении — на отметке +3 метра.
В физике перемещение часто обозначают символом ( s ), т.е. в данном случае ( s ) равно 3 метрам.
Как и любое другое измерение в физике, перемещение выражается в некоторых единицах, обычно в сантиметрах или метрах. Но часто можно встретить и другие единицы: километр, дюйм, фут, миля или даже световой год (расстояние, которое проходит свет за один год и которое тяжело измерить обычной линейкой; оно приблизительно равно 9 460 800 000 000 километрам или 9 460 800 000 000 000 метрам).
Ученые любят очень подробно описывать разные ситуации. Например, исходное положение часто обозначают символом( s_0 )(или, в англоязычной литературе,( s_i ) где ( i ) обозначает “initial”, т.е. исходный). А конечное положение часто обозначают символом ( s_1 ) (или, в англоязычной литературе, ( s_f ) где ( f ) обозначает “final”, т.е. конечный). Таким образом, положения на схеме А и схеме Б на рис. 3.1 выражаются символами ( s_0 ) и ( s_1 ) соответственно. А перемещение ( s ) между ними равно их разности, т.е. конечное положение минус исходное положение:
Перемещения не обязательно должны быть положительными: они могут быть нулевыми или даже отрицательными. На схеме В на рис. 3.1 показана ситуация, когда неугомонный мячик переместился в новое положение у отметки -4 метра. Чему равно перемещение в этом случае? Ответ зависит от выбранного исходного положения. Исходное положение также часто называют начальной точкой (в которой начинается действие), которую можно выбрать произвольным образом. Если в качестве исходного положения выбрать положение 0 на линейке, то получим следующее перемещение:
Обратите внимание, что ( s ) отрицательно!
В качестве начальной точки можно выбрать отличное от 0 положение. Например, для перехода между исходным положением на схеме А на рис. 3.1 и конечным положением на схеме В получим следующее перемещение:
Величина перемещения зависит от выбора начальной точки. В простых задачах выбор начальной точки очевиден, а как быть в более сложных случаях, например, когда движение происходит не вдоль линейки?
Разбираемся с осями
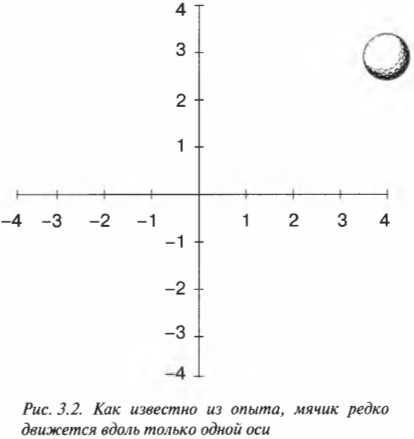
В реальном мире объекты редко движутся вдоль линеек, как мячик для гольфа на рис. 3.1. Часто движение происходит в двух или даже трех измерениях пространства. Чтобы измерить движение в двух пространственных измерениях, нужно иметь две пересекающиеся линейки, которые называются осями. Горизонтальную ось называют осью X, а вертикальную — осью Y, а при движении в трехмерном пространстве используют еще одну ось Z (если представить, что оси X и Y лежат в плоскости страницы, то ось Z как бы “торчит” из нее).
На рис. 3.2 показан пример движения мячика для гольфа в двумерном пространстве. Мячик движется из центра рисунка в верхний правый угол.
Используя оси, можно сказать, что мячик передвинулся на +4 метра по оси X и на +3 метра по оси Y. Новое положение мячика обозначается парой чисел (4; 3), где первое число относится к оси X, а второе — к оси Y, т.е. оно выражается в формате ( (x,y) ).
Чему равно перемещение? Изменение положения по оси X обозначается символом ( Delta x ) (греческий символ ( Delta ) произносится “дельта” и означает “изменение”) и равно: конечное положение минус исходное положение. Если мячик стартует из центра рисунка, т.е. из положения (0; 0), то изменение положения по оси X равно:
Аналогично, изменение положения по оси Y равно:
Допустим, что нужно вычислить величину суммарного перемещения по обеим осям X и Y. Иначе говоря, насколько далеко удалился мячик от исходного положения в центре рисунка? Это можно подсчитать на основе теоремы Пифагора, т.е. выполнить следующие вычисления:
Итак, величина перемещения мячика равна 5 метрам.
Согласно теореме Пифагора, сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Измеряем скорость
В предыдущих разделах рассматривалось движение в одном или двух пространственных измерениях. Однако реальные перемещения происходят за некоторый промежуток времени, т.е. с некоторой скоростью. Например, за какое время произошло перемещение на рис. 3.1 из исходного положения в конечное положение: за 12 лет или 12 секунд?
Остальная часть этой главы посвящена измерению скорости перемещений. Аналогично измерению перемещения в пространстве, можно измерять разницу во времени между началом и концом движения, которая обычно выражается следующим образом:
Здесь ( t_1 ) обозначает конечное время, ( t_0 ) — начальное время, а их разность — количество времени, необходимого для перемещения, например движения мячика от начального к конечному положению. Когда ученые хотят узнать, насколько быстро происходит это событие, то фактически это значит, что они хотят измерить скорость.
Подробнее о скорости: что же это такое
Наверняка вам известно из опыта, что скорость определяется следующим образом:
скорость = расстояние/время.
Например, если расстояние ( s ) пройдено за время ( t ), то скорость ( v ) равна:
Переменная ( v ) обозначает только величину скорости, но истинная скорость также имеет направление (более подробно это описывается в главе 4). Иначе говоря, скорость является вектором (векторы обычно обозначаются полужирным начертанием, например ( mathbf{v} )). Векторы обладают величиной и направлением, т.е., зная скорость, мы знаем не только быстроту, но и направление движения. Аналогично, перемещение в более общем смысле является вектором, т.е. характеризуется не только величиной, но и направлением смещения (более подробно векторы описываются в главе 4).
Достаточно просто, не так ли? Точнее говоря (физики очень любят точность), скорость равняется изменению положения, деленному на изменение времени. Потому скорость движения вдоль оси X можно выразить следующим образом:
В реальном мире скорость может принимать очень разные формы, некоторые из них описываются в следующих разделах.
Смотрим на спидометр: мгновенная скорость
Итак, у нас уже есть общее представление о скорости. Именно ее измеряет спидометр автомобиля, не так ли? Когда вы катите по прямолинейному шоссе, все, что нужно делать, — всего лишь следить за показаниями спидометра. “Уже 140 километров в час. Пожалуй, сбросим скорость до 120”. Именно так мы часто поступаем в жизни, а иначе говоря, так мы определяем мгновенную скорость.
Понятие мгновенной скорости играет важную роль в понимании физических процессов. В данный момент времени спидометр показывает 120 километров в час, значит, ваша мгновенная скорость равна именно этой величине. Если вы ускоритесь до 150 километров в час, то ваша мгновенная скорость станет равной этой новой величине. Мгновенная скорость — это скорость в данный момент времени. Спустя две секунды мгновенная скорость может стать совершенно другой.
Движемся постоянно: равномерная скорость
А что если долгое время автомобиль едет со скоростью 120 километров в час? В физике эта скорость называется равномерной (или постоянной), а в жизни она возможна только при движении на абсолютно ровных и прямолинейных дорогах, когда долгое время можно поддерживать движение без изменения скорости.
Равномерное движение с постоянной скоростью является простейшим видом движения, поскольку оно никак не меняется.
Движемся вперед и назад: неравномерное движение
Название этого типа движения говорит само за себя: неравномерное движение означает движение со скоростью, меняющейся со временем. Именно с такой скоростью мы чаще всего сталкиваемся в повседневной жизни. Вот как выглядит уравнение изменения скорости от исходной скорости ( v_1 ) до конечной скорости ( v_0 ):
Остальная часть этой главы посвящена ускорению, которое характеризует неравномерность движения.
Жмем на секундомер и определяем среднюю скорость
Выражение со скоростями не так уж неосязаемо, как может показаться. Измерения скорости можно сделать более конкретными. Допустим, что вам хочется совершить путешествие из Нью-Йорка в Лос-Анджелес, которые находятся на расстоянии около 2781 миль друг от друга. Если предположить, на это путешествие ушло 4 суток, то какой была ваша скорость?
Скорость можно найти, если поделить пройденное расстояние на затраченное на это время:
Итак, результат 695,3 получен, но в каких единицах он выражен?
В этом выражении мили делятся на сутки, т.е. результат равен 695,3 милям в сутки. Это не совсем стандартная единица измерений и вполне естественно было бы поинтересоваться: а сколько это миль в час? Для ответа на этот вопрос нужно перевести сутки в часы, как показано в главе 2. Поскольку в сутках 24 часа, то получим следующий результат:
Итак, получен более понятный результат 28,97 миль в час. Смущает лишь столь малая величина скорости, ведь обычно машины едут со скоростью в 2-3 раза быстрее, однако среднюю скорость для всего путешествия мы вычислили, разделив все расстояния на все время, включая время отдыха.
Среднюю скорость часто обозначают с помощью штриха над переменной: ( overline{v} ) .
Средняя скорость и неравномерное движение
Средняя скорость отличается от мгновенной, если только вы не движетесь равномерно, когда скорость вообще не меняется. А средняя скорость неравномерного движения, когда все расстояние делится на все время, может отличаться от мгновенной скорости.
Путешествуя из Нью-Йорка в Лос-Анджелес, вам наверняка придется провести несколько ночей в отелях, и во время вашего отдыха мгновенная скорость автомобиля равна 0 миль в час, а средняя скорость — 28,97 миль в час! Дело в том, что средняя скорость получена в результате деления всего расстояния на все время.
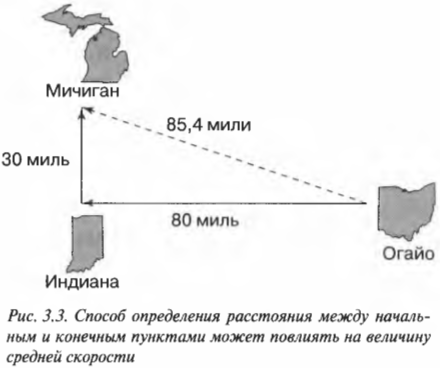
Средняя скорость может зависеть от фактически пройденного пути. Допустим, что, путешествуя по штату Огайо, вы решили подвезти попутчика в штат Индиана и погостить у вашей сестры в штате Мичиган. Все путешествие может иметь вид, показанный на рис. 3.3: первые 80 миль — в штат Индиана, а потом 30 миль — в штат Мичиган.
Если ехать со скоростью 55 миль в час, то для преодоления всего пути длиной 80 + 30 = 110 миль потребуется 2 часа. Но если взять расстояние по прямой между начальной и конечной точкой путешествия, которое равно 85,4 миль, то средняя скорость будет равна:
Таким образом, получена средняя скорость для расстояния от начальной до конечной точки путешествия вдоль пунктирной линии. Но если вам нужно определить скорость для каждого из двух отрезков фактически пройденного пути, то нужно измерить длину каждого из двух отрезков и разделить их на время их прохождения.
При движении с равномерной скоростью это можно сделать легко и просто, поскольку в таком случае средняя скорость равняется мгновенной скорости в любой точке пути.
Изучая движение, нужно учитывать не только скорость, но и направление движения. Именно по этой причине огромное значение имеет понятие вектора скорости. Более подробно векторы описываются в главе 4.
Ускоряемся и замедляемся
Как и в случае со скоростью, вам уже наверняка знакомо понятие ускорения. Ускорение характеризует быстроту изменения скорости. При выезде с подземной парковки порой приходится слышать визг шин — кто-то пытается ускориться, подрезать и обогнать вас на выезде. Вот он проскакивает перед вами буквально в нескольких сантиметрах и резко тормозит прямо перед вами, принуждая вас резко нажать на педаль тормоза. Именно в таких ситуациях очень полезно и важно знать основы физики.
Определяем ускорение
С точки зрения физики ускорение (( a )) — это изменение скорости (( Delta v )) за единицу времени (( Delta t )):
Это соотношение можно переписать иначе для известных начальной и конечной скоростей в начальный и конечный моменты времени соответственно:
Ускорение, как и скорость, является векторной величиной и часто обозначается полужирным начертанием: ( mathbf{a} ). Иначе говоря, ускорение, как и скорость, характеризуется направлением. Более подробно векторы описываются в главе 4.
Определяем единицу ускорения
Единицу ускорения можно легко определить, если проанализировать определение ускорения, в котором изменение скорости делится на изменение времени:
Подставляя единицы измерения, получим:
Итак, единица ускорения — это единица расстояния, деленная на единицу времени в квадрате. Иначе говоря, ускорение — это скорость изменения скорости.
Поскольку ускорение — это расстояние, деленное на время в квадрате, то среди единиц измерения можно встретить следующие: километр на секунду в квадрате, метр на секунду в квадрате, сантиметр на секунду в квадрате, миля на секунду в квадрате, фут на секунду в квадрате и т.д.
Шутки ради допустим, что вы едете со скоростью 75 миль в час и в зеркале заднего вида видите проблесковый маячок дорожного патруля. Жмете на тормоза и останавливаетесь спустя 20 секунд. Инспектор дорожного патруля подходит к вам и сообщает: “Выдвигались со скоростью 75 миль в час в зоне, где скорость движения ограничена величиной 30 миль в час”. Что можно ответить? Попробуйте поразить воображение инспектора своими познаниями физики.
Быстро подсчитайте величину своего замедления после сигнала инспектора, чтобы поразить его своим исключительным законопослушанием! Достаньте калькулятор и начните вводить в него данные. Преобразуйте величину скорости 75 миль в час в более впечатляющие единицы измерения, например в сантиметры в секунду. Для этого сначала преобразуйте единицу измерения скорости, т.е. выразите ее в милях в секунду:
Теперь попробуем преобразовать мили в секунду в более впечатляющие для инспектора единицы измерения, например в сантиметры в секунду. Как известно, 1 миля содержит 5280 футов, а 1 фут — 12 дюймов. Тогда пройденное расстояние в дюймах в секунду равно:
В главе 2 уже упоминалось, что 1 дюйм равен 2,54 сантиметрам, потому пройденное расстояние в сантиметрах в секунду равно:
Таким образом исходная скорость движения была равна 3,4⋅103 сантиметров в секунду, а конечная — 0 сантиметров в секунду. Это изменение скорости произошло за 20 секунд. Так чему же равняется ускорение? Напомним еще раз формулу ускорения:
Подставляя числа, получим:
Итак, ускорение равно 170 см/с2. Однако попробуем присмотреться к этому результату более внимательно и вспомнить точное определение ускорения:
Конечная скорость равна 0 см/с, а исходная — 3,4⋅103 см/с, так что подставляя значения в эту формулу, получим:
Иначе говоря, мы получили -170 см/с2, а не +170 см/с2, что с точки зрения физики (и законов дорожного движения) имеет большое значение. Если бы ваше ускорение было равно +170 см/с2, то конечная скорость через 20 секунд была бы равна 150 миль в час, а не 0 миль в час. Ни один инспектор дорожного движения не обрадовался бы такому конечному результату.
Теперь вам осталось только очаровательно улыбнуться и сказать инспектору: “Возможно, я ехал несколько быстрее, чем следовало, но я чрезвычайно законопослушный гражданин и, едва услышав вашу сирену, мгновенно затормозил с замедлением -170 см/с2”. Возможно, инспектор будет настолько впечатлен этим результатом и вашими познаниями физики, что отпустит вас без наказания.
Аналогично скорости, ускорение может принимать разный вид в разных физических задачах. Ускорение может быть положительным, отрицательным, средним, мгновенным, равномерным или неравномерным. В следующих разделах описываются некоторые такие ситуации.
Положительное и отрицательное ускорение
При решении физических задач всегда нужно внимательно следить за знаком используемой величины. Ускорение, как и скорость, может быть отрицательным или положительным. При торможении автомобиля его скорость меняется с положительной до 0, а потому ускорение имеет отрицательный знак.
Ускорение, как и скорость, обладает знаком.
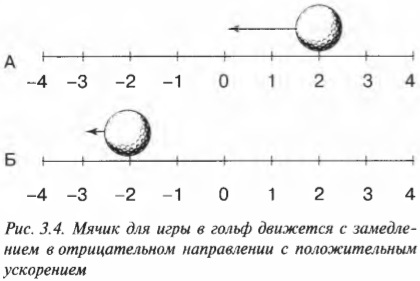
Не следует думать, что отрицательное ускорение всегда означает замедление, а положительное ускорение всегда означает ускорение. На рис. 3.4 показан пример ситуации, когда мячик для игры в гольф движется с замедлением из начального положения (схема А на рис. 3.4) в конечное положение (схема Б на рис. 3.4), но с положительным ускорением.
Поскольку отрицательная величина скорости уменьшается, то в целом ускорение мячика имеет положительную величину. Иначе говоря, для уменьшения отрицательной скорости нужно сделать положительное приращение скорости, т.е. ускорение при этом будет положительным.
Знак ускорения сообщает нам о том, как меняется скорость. Положительное ускорение означает, что скорость увеличивается в положительном направлении и уменьшается в отрицательном направлении. И наоборот, отрицательное ускорение означает, что скорость увеличивается в отрицательном направлении и уменьшается в положительном направлении.
Среднее и мгновенное ускорение
Аналогично скорости, ускорение может иметь мгновенное или среднее значение. Среднее ускорение равно отношению изменения скорости к изменению времени. Среднее ускорение обозначается штрихом сверху, ( overline{a} ), и вычисляется аналогично средней скорости, т.е. от конечной скорости отнимается начальная скорость и полученная разность делится на все время (т.е. на разность конечного и начального времени):
Это соотношение дает нам среднее ускорение, но фактическое ускорение в произвольный момент времени не всегда равно среднему ускорению. Например, в предыдущем примере после того, как вы заметили сигнал инспектора, вы очень сильно нажимаете педаль тормоза, и автомобиль тормозит с очень большим ускорением. Но перед самой остановкой вы отпускаете педаль тормоза, и ваш автомобиль тормозит с уже меньшим ускорением. Оба эти мгновенные значения отличаются от величины среднего ускорения, вычисленного после деления всего изменения скорости на все время торможения.
Равномерное и неравномерное ускорение
Движение с неравномерным ускорением означает движение с изменением ускорения. Например, при движении в городе часто приходится тормозить перед знаками и сигналами остановки движения, а потом снова разгоняться.
Однако существуют ситуации, когда ускорение остается неизменным во время движения, например ускорение свободного падения под действием силы притяжения Земли. Это ускорение в общем случае равно 9,8 метров в секунду в квадрате, направлено к центру Земли и неизменно.
Связываем ускорение, время и перемещение
Итак, в этой главе вы познакомились с четырьмя параметрами движения: ускорением, скоростью, временем и перемещением. Перемещение и время связаны следующим простым соотношением для скорости:
Аналогично, скорость и время связаны следующим простым соотношением для ускорения:
Однако эти соотношения связывают только по два “уровня” переменных, т.е. скорость с перемещением и временем, а ускорение со скоростью и временем. А как связать три “уровня” переменных, т.е. ускорение со временем и перемещением?
Допустим, что вы участвуете в гонке и после пробного заезда хотели бы знать ускорение, которое способен обеспечить ваш автомобиль по известному пройденному пути 402 метра за 5,5 секунд. Таким образом, получается задача, в которой нужно связать ускорение с перемещением и временем.
Итак, для решения этой задачи нужно вывести уравнение связи ускорения с перемещением и временем.
Работу с уравнениями можно заметно упростить, если использовать алгебраические подстановки, например использовать переменную ( v ) вместо разности ( v_1-v_0 ) и переменную ( t ) вместо разности ( t_1-t_0 ). В случае необходимости после получения решения можно сделать обратную подстановку, заменяя переменную ( v ) разностью ( v_1-v_0 ) и переменную ( t ) разностью ( t_1-t_0 ).
Не такие уж и далекие связи
Попробуем связать ускорение, перемещение и время, жонглируя разными переменными, пока не получим нужный результат. Перемещение равно средней скорости, умноженной на время:
Итак, у нас есть отправная точка. Какова средняя скорость автомобиля из предыдущего примера? Начальная скорость была равна 0, а конечная — очень большой. Поскольку ускорение было постоянным, то скорость росла линейно от нуля до конечного значения (рис. 3.5).
При постоянном ускорении средняя скорость равна половине суммы конечной и начальной скоростей:
Конечная скорость равна:
Тогда средняя скорость равна:
Теперь подставим это выражение для средней скорости в уравнение для перемещения ( s=overline{v}t ) и получим:
Теперь вместо переменной ( t ) можно подставить исходную разность конечного и начального моментов времени и получим:
Ура! Мы вывели одно из наиболее важных соотношений между ускорением, перемещением, временем и скоростью, которые используются в физических задачах.
Выводим более сложные соотношения
А что если движение началось не с нулевой начальной скоростью? Как в таком случае связать ускорение, время и перемещение? Как такое начальное значение скорости, например 100 миль в час, повлияет на величину пройденного расстояния? Поскольку расстояние равно скорости, умноженной на время, то искомое соотношение имеет следующий вид:
Такое выражение не так уж и легко запомнить, если, конечно, вы не обладаете фотографической памятью. Сложно даже запомнить более простую формулу связи между перемещением и временем для движения с постоянным ускорением, с нулевого начального момента и с нулевой начальной скоростью:
Если движение начинается не с нулевой скоростью, то к предыдущему выражению нужно добавить расстояние, которое было бы пройдено за то же время с начальной скоростью. Подобные соображения на основе здравого смысла значительно упрощают решение физических задач. Механическое запоминание формул без понимания их смысла не всегда поможет вам найти ошибку в вычислениях.
Так каким же было ускорение автомобиля в одном из предыдущих примеров? Теперь мы знаем, как связаны перемещение, ускорение и время, и для ответа на этот вопрос нужно применить алгебраические навыки. Итак, мы имеем:
После деления обеих частей на ( t^2 ) и умножения на 2 получим:
Великолепно! Подставляя числа, получим:
Итак, получилось, что ускорение автомобиля равно 27 метров в секунду в квадрате. Насколько велико это ускорение? Например, ускорение свободного падения в поле тяготения Земли, ( g ), равно около 9,8 метров в секунду в квадрате, т.е. ускорение автомобиля приблизительно равно ( 2,7g ).
Связываем скорость, ускорение и перемещение
До сих мы достаточно успешно справлялись со всеми предложенными задачами. А что если немножко усложнить их условия? Допустим, что в примере с автомобилем вам известно только ускорение 26,3 метров в секунду в квадрате и конечная скорость 146,3 метров в секунду, а нужно определить пройденное расстояние. Справитесь ли вы с таким заданием? Внимательный читатель уверенно ответит: “Никаких проблем, только дайте мне калькулятор”.
Прежняя задача в новой формулировке кажется более сложной, поскольку в прежних соотношениях всегда присутствовало время. Это значит, что, зная время движения, вы легко сможете решить задачу даже в новой более сложной формулировке. Чтобы определить время движения, достаточно знать ускорение, а также начальную и конечную скорости.
Поскольку:
то получим выражение для времени движения:
Теперь, зная время, можно определить пройденное расстояние по формуле:
Второй член можно исключить, потому что ( v_0 ) = 0. Итак, после подстановки чисел получим:
Как выглядит формула связи перемещения, ускорения и скорости? Для ее получения нужно найти выражение для времени движения:
Поскольку при движении с равномерным ускорением ( s=overline{v}t ), a ( overline{v}={}^1!/!_2(v_1-v_0) ), то получим:
Подставляя в эту формулу выражение для времени движения, получим:
После несложных алгебраических преобразований получим:
Перемещая член ( 2a ) в другую часть уравнения, получим еще одно важное соотношение, которое связывает скорость, ускорение и перемещение:
Уф, это выражение стоит запомнить!
После решения всех этих задач каждый читатель по праву может считать себя повелителем движения.
Глава 3. Утоляем жажду скорости
4.2 (84%) 5 votes