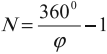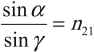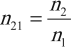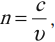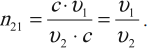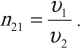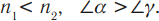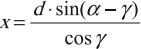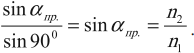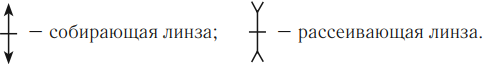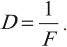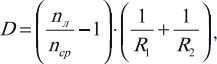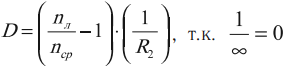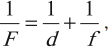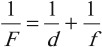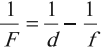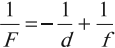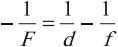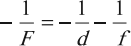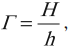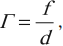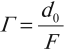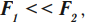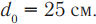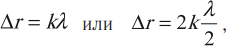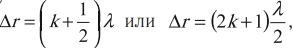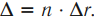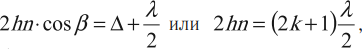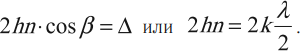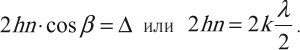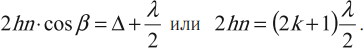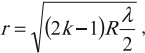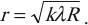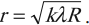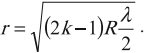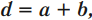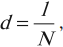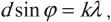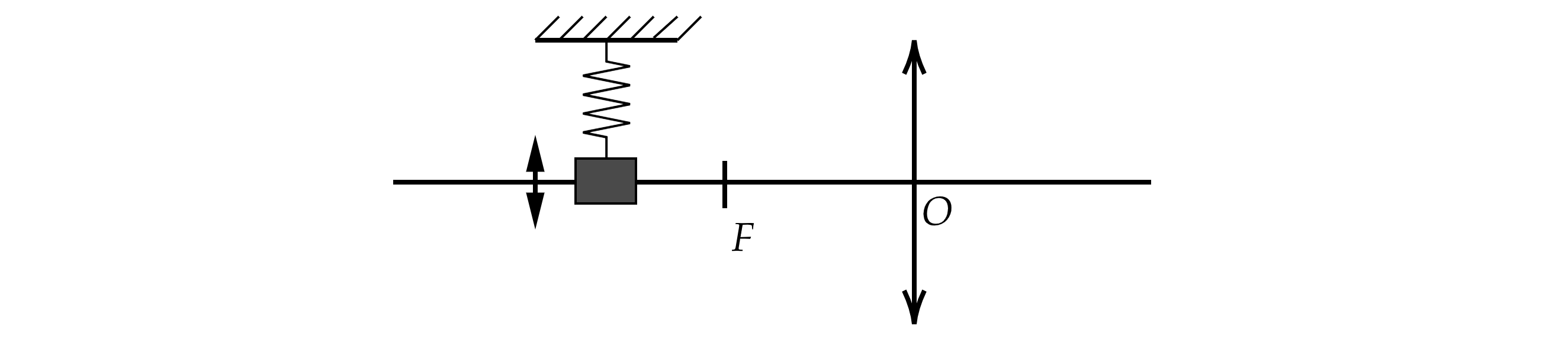Формула тонкой линзы — формула, связывающая три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы.
Условные обозначения:
- расстояние от предмета до линзы — d (м);
- расстояние от изображения до линзы— f (м);
- фокусное расстояние линзы — F (м).
Вывод формулы
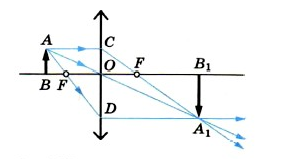
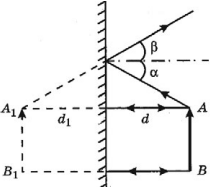
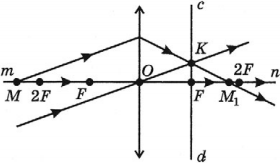
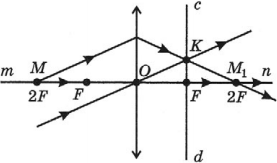
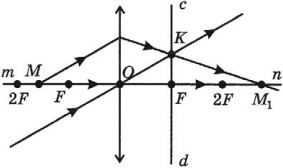
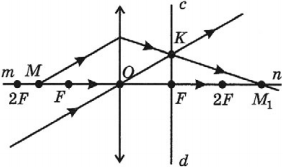
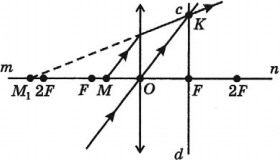
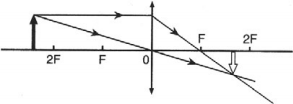
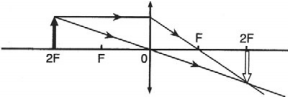
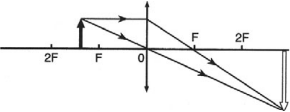
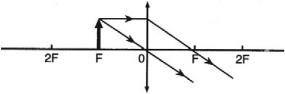
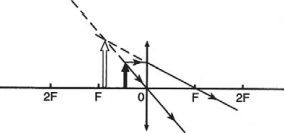
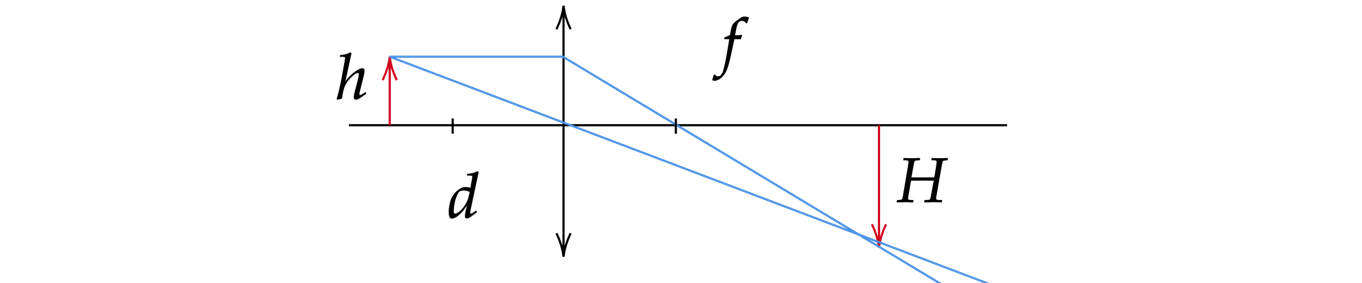
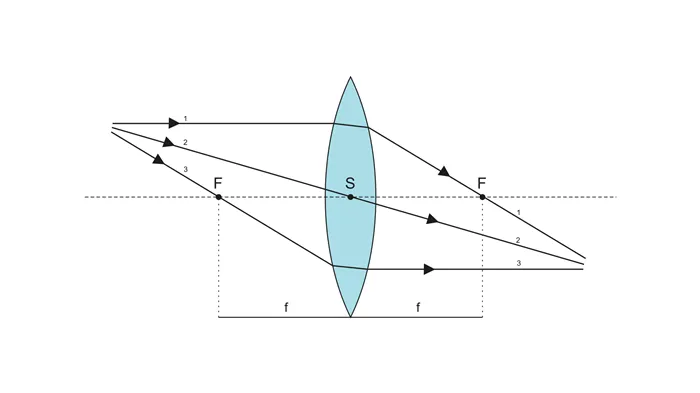
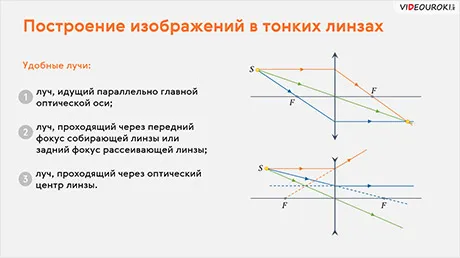
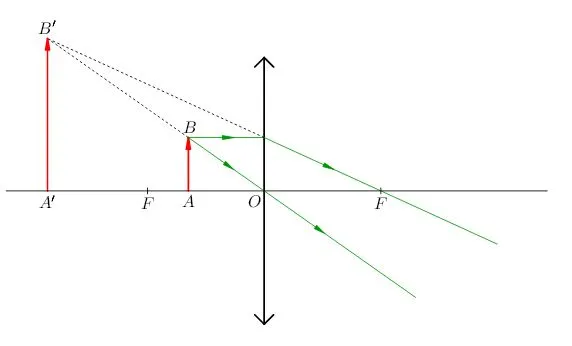
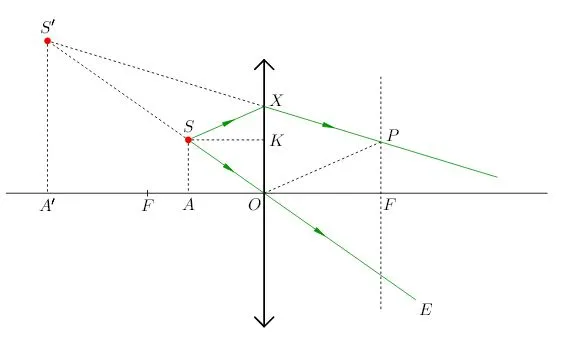
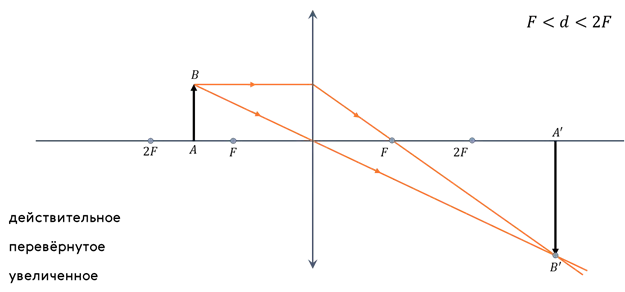
Обратимся к рисунку, который мы использовали для объяснения правила построения изображений в собирающих линзах:
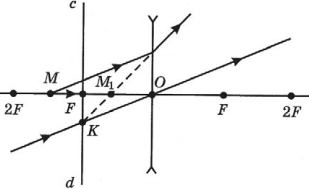
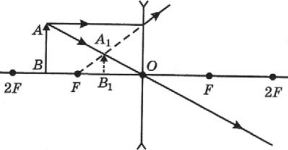
Видно, что треугольники АОВ и А1В1О подобные (по двум углам). Следовательно:
BOOB1=ABA1B1
По двум углам также являются подобными треугольники COF и FA1B1. Отсюда делаем вывод, что:
COA1B1=OFFB1
Линия предмета образует с частью главной оптической оси, перпендикуляром, проведенным из верхней точки к линзе, и частью самой линзы прямоугольник. Следовательно, его противоположные стороны равны:
AB=CO
Следовательно:
ABA1B1=COA1B1
Отсюда следует, что:
BOOB1=OFFB1
BO является расстоянием от предмета до линзы. Обозначим его за d. OB1 является расстоянием от линзы до изображения. Обозначим его за f. OF является фокусным расстоянием линзы. Обозначим его за F. FB1 является разностью расстояния от линзы до изображения и фокусного расстояния линзы. Поэтому это выражение мы можем записать так:
df=Ff−F
Избавимся от знаменателей и получим:
fd−Fd=fF
Или можно записать так:
fF+Fd=fd
Теперь все члены равенства поделим на произведение Ffd. В результате вычислений получим формулу тонкой линзы:
Формула тонкой линзы
1d+1f=1F
Поскольку величиной, равной обратной фокусному расстоянию, является оптическая сила, формулу тонкой линзы можно записать следующим образом:
1d+1f=D
Величины d, ƒ и F могут быть как положительными, так и отрицательными. Отметим (без доказательства), что при применении формулы тонкой линзы знаки нужно ставить перед членами уравнения согласно следующим правилам.
Правила расстановки знаков перед членами уравнения в формуле линзы
- Если линза собирающая, то ее фокус действительный, и перед членом 1F ставят знак «плюс» (1F).
- Если линза рассеивающая, то ее фокус мнимый, и перед членом 1F ставят знак «минус» (−1F).
- Если изображение действительное, то перед величиной 1d ставят знак «плюс» (1d).
- Если изображение мнимое, то перед величиной 1d ставят знак «минус» (−1d).
- Величина 1f всегда имеет знак «плюс», поскольку расстояние от предмета до линзы всегда положительное.
Иногда случается, что перед величинами F, f и d знаки неизвестны. Тогда при вычислениях перед ними ставят знаки «плюс». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.
Пример №1. Фокусное расстояние линзы равно 10 см. Найти расстояние от предмета до линзы, если расстояние от нее до изображения составляет 15 см.
Переводить в СИ единицы измерения не будем, поскольку они однородны. Так как все величины выражены в см, то и ответ будет выражен в см.
Применим формулу тонкой линзы:
1d+1f=1F
1d+115=110
Умножим выражение на 150d:
150+10d=15d
5d=150
d=30 (см)
Увеличение линзы
Раньше мы уже упоминали, что изображение, полученное в линзе, может быть увеличенным или уменьшенным. Различие размеров предмета и изображения характеризуется увеличением.
Определение
Линейное увеличение — отношение линейного размера изображения к линейному размеру предмета. Линейное увеличение обозначают буквой Γ.
Чтобы найти линейное увеличение изображения предмета в линзе, снова обратимся к первому рисунку этого параграфа. Если высота предмета АВ равна h, а высота изображения А1В1 равна Н, то:
Γ=Hh
Мы уже выяснили, что треугольники АОВ и ОА1В1 подобны. Поэтому:
Hh=|f||d|
Где H — высота изображения предмета, h — высота самого предмета.
Отсюда вытекает, что увеличение линзы равно:
Γ=|f||d|
Пример №2. Предмет имеет высоту h = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная от экрана на расстоянии f = 4 м, чтобы изображение указанного предмета имело высоту H = 1 м?
2 см = 0,02 м
Сначала применим формулы тонкой линзы:
1d+1f=1F
Она необходима, чтобы выразить фокусное расстояние линзы:
F=dfd+f
Расстояние от предмета до линзы неизвестно. Но его можно выразить из формулы увеличения линзы:
Γ=fd=Hh
Отсюда это расстояние равно:
d=fhH
Подставим полученное выражение в формулу фокусного расстояния линзы:
F=fhHffhH+f=f2hH·
Hfh+fH=fhH+h
F=fhH+h=4·0,021+0,02≈0,08 (м)=8 (см)
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
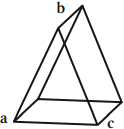
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
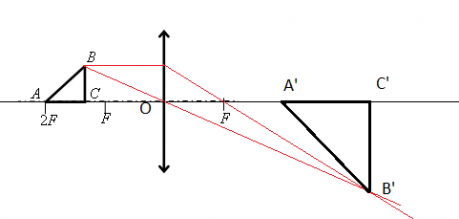
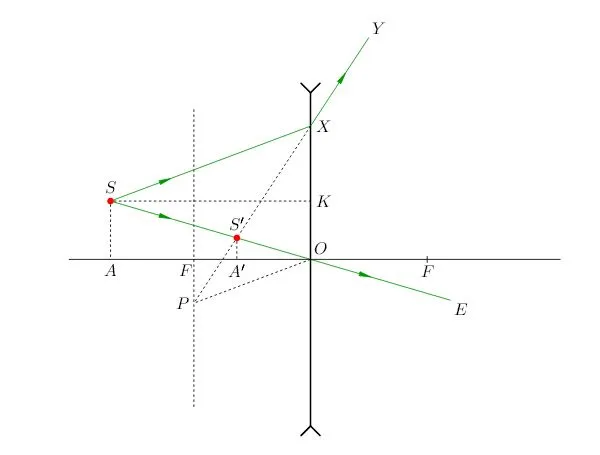
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17685
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Ответ:
а) 0,50 м
б) 0,75 м
в) 1,25 м
г) 1,50 м
Линза с фокусным расстоянием F=1м даёт на экране изображение предмета, увеличенное в 4 раза. Каково расстояние от предмета до линзы?
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы и формулу тонкой линзы.
3.Выразить из обеих формул расстояние от линзы до изображения предмета.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Фокусное расстояние линзы: F = 1 м.
• Увеличение линзы: Γ = 4.
Запишем формулу увеличения линзы и выразим из нее расстояние от линзы до изображения предмета:
Γ=fd
f=Γd
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Γd=dFd−F
Поделим на d и выразим расстояние от предмета до линзы:
Γ=Fd−F
d=FΓ+F=14+1=1,25 (м)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18124
Предмет высотой 6 см расположен на горизонтальной главной оптической оси тонкой собирающей линзы на расстоянии 30 см от её оптического центра. Высота изображения предмета 12 см. Найдите фокусное расстояние линзы.
Ответ:
а) 5 см
б) 10 см
в) 20 см
г) 36 см
Алгоритм решения
1.Записать известные данные.
2.Записать формулу увеличения линзы в двух вариантах и выразить из нее расстояние от изображения до линзы.
3.Записать формулу тонкой линзы и тоже выразить из нее расстояние от изображения до линзы.
4.Приравнять правые части выражений.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем известные данные:
• Расстояние от оптического центра линзы до предмета: d = 30 cм.
• Высота предмета: h = 6 см.
• Высота изображения: H = 12 см.
Так как все данные измеряются в сантиметрах, переводить единицы измерения величин в СИ нет необходимости. Просто ответ будет получен тоже в сантиметрах.
Запишем формулу увеличения линзы:
Γ=Hh=fd
Отсюда расстояние от изображения до линзы равно:
f=Hdh
Запишем формулу тонкой линзы и выразим из нее расстояние от линзы до изображения предмета:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Приравняем правые части последних выражений:
Hdh=dFd−F
Поделим на d, у множим на h(d –F) и выразим фокусное расстояние:
Hh=Fd−F
H(d−F)=hF
Hd−HF=hF
hF+HF=Hd
F(h+H)=Hd
F=Hdh+H=12·3012+6=20 (см)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19112
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
3.Записать формулу тонкой линзы и определить из нее расстояние от изображения до линзы.
4.Записать формулу линейного увеличения линзы двумя способами для вычисления радиусов окружностей, по которым движутся точка и ее изображение.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Фокусное расстояние линзы: F = 10 см.
• Расстояние от линзы до плоскости, в которой вращается точка: d = 15 см.
• Скорость вращения точки: v = 5 м/с.
10 см = 0,1 м
15 см = 0,15 м
Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.
Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:
Γ=Rr
Линейное увеличение также определяется формулой:
Γ=fd
Следовательно:
Rr=fd
Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:
Rr=dFd(d−F)=Fd−F
Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:
ω=vr=VR
Отсюда линейная скорость движения изображения равна:
V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
Оптика
Оптика – это раздел физики, в котором изучаются закономерности световых явлений, природа света и его взаимодействие с веществом.
Световой луч – это линия, вдоль которой распространяется свет.
Закон независимости световых лучей:
при пересечении световых лучей каждый из них продолжает распространяться в прежнем направлении.
Источник света – это тело, которое излучает свет.
При излучении света источник теряет энергию, при поглощении его внутренняя энергия увеличивается, т. е. распространение света сопровождается переносом энергии.
Виды источников света:
- тепловые – это источники, в которых излучение света происходит в результате нагревания тела до высокой температуры;
- люминисцентные – это тела, излучающие свет при облучении их светом, рентгеновскими лучами, радиоактивным излучением и т. д.
Точечный источник света – это источник, представляющий собой светящуюся материальную точку, т. е. источник, размеры которого малы по сравнению с расстоянием до освещаемого предмета.
Если источник света находится в бесконечности, то его лучи падают на поверхность параллельным пучком.
Свет – это электромагнитная волна с частотой от 1,5·1011 Гц до 3·1016 Гц.
Скорость света в вакууме: ( c ) = 3·108 м/с.
Содержание
- Прямолинейное распространение света
- Закон отражения света
- Построение изображений в плоском зеркале
- Закон преломления света
- Полное внутреннее отражение
- Линзы. Оптическая сила линзы
- Формула тонкой линзы
- Построение изображений в линзах
- Оптические приборы. Глаз как оптическая система
- Интерференция света
- Дифракция света
- Дифракционная решетка
- Дисперсия света
- Основные формулы по теме «Оптика»
Прямолинейное распространение света
Закон распространения света:
свет в прозрачной однородной среде распространяется прямолинейно.
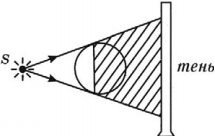
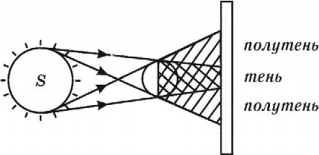
Экспериментальным доказательством прямолинейности распространения света является образование тени.
Тень – это область пространства, куда не попадает свет от источника.
Полутень – это область пространства, куда частично попадает свет от источника.
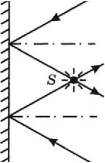
Если источник света точечный, то на экране образуется четкая тень предмета.
Если источник неточечный, то на экране образуется размытая тень (области тени и полутени).
Образованием тени при падении света на непрозрачный предмет объясняются такие явления, как солнечное и лунное затмения.
Закон отражения света
Отражение – это явление, при котором при падении световых лучей на непрозрачную гладкую поверхность они меняют направление распространения, возвращаясь в прежнюю среду.
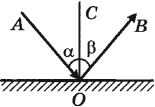
АО – падающий луч, ОВ – отраженный луч, СО – перпендикуляр
Угол падения – это угол между падающим лучом и перпендикуляром к отражающей поверхности.
Угол отражения – это угол между отраженным лучом и перпендикуляром к отражающей поверхности.
Законы отражения света
- Лучи падающий и отраженный лежат в одной плоскости с перпендикуляром, восстановленным в точку падения луча к отражающей поверхности.
- Угол отражения равен углу падения. ( anglebeta=anglealpha ), где ( alpha ) – угол падения, ( beta ) – угол отражения.
Виды отражения
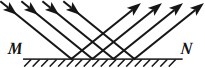
- Зеркальное – это отражение, при котором лучи, падающие на поверхность параллельным пучком, после отражения остаются параллельны.
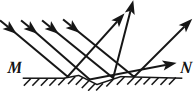
- Рассеянное – это отражение, при котором лучи, падающие на поверхность параллельным пучком, после отражения отклоняются в различных направлениях.
Если луч падает перпендикулярно отражающей поверхности, то угол падения равен нулю, и угол отражения тоже равен нулю. Поэтому луч отражается в обратном направлении.
Важно!
В оптике все углы отсчитываются от перпендикуляра к отражающей поверхности или к границе раздела сред.
Построение изображений в плоском зеркале
Построение изображения в плоском зеркале основано на законах отражения света.
Алгоритм построения изображения в плоском зеркале
- Проведите из данной точки на поверхность луч под произвольным углом. В точке падения луча на границу раздела сред проведите перпендикуляр.
- Отметьте угол падения ( alpha ).
- Постройте равный ему угол отражения ( beta ).
- Проведите из данной точки перпендикуляр к поверхности зеркала ( (alpha=0) ).
- Постройте равный ему угол отражения ( (beta=0) ) (эти лучи совпадают).
- Проведите пунктирной линией продолжения отраженных лучей за зеркало.
- Найдите точку пересечения продолжений отраженных лучей (эта точка является изображением данной точки в плоском зеркале).
- Аналогично постройте изображение второй точки.
- Соедините полученные изображения точек пунктирной линией.
Изображение предмета в плоском зеркале мнимое, прямое, по размерам равное предмету, находящееся за зеркалом на таком же расстоянии, на каком предмет находится перед зеркалом.
Важно!
Если на поверхность плоского зеркала падает сходящийся пучок лучей, то изображение получается действительным.
Если поверхность двух плоских зеркал образует угол ( varphi ), то количество изображений в такой системе зеркал можно определить по формуле:
где ( N ) – количество изображений.
Закон преломления света
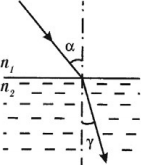
Преломление света – это изменение направления распространения светового луча на границе раздела двух сред.
Угол преломления – это угол между преломленным лучом и перпендикуляром к границе раздела двух сред.
( gamma ) – угол преломления
Законы преломления света
- Лучи падающий и преломленный лежат в одной плоскости с перпендикуляром, восстановленным в точку падения луча к преломляющей поверхности.
- Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред и равная относительному показателю преломления двух сред:
где ( n_{21} ) – относительный показатель преломления.
Первой является среда, в которой распространяется падающий луч, второй является среда, в которой распространяется преломленный луч.
Относительный показатель преломления равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:
где ( n_1 ) – абсолютный показатель преломления первой среды; ( n_2 ) – абсолютный показатель преломления второй среды.
Абсолютный показатель преломления показывает, во сколько раз скорость света в вакууме больше, чем в данной среде:
где ( c ) – скорость света в вакууме, ( v ) – скорость распространения света в данной среде.
Относительный показатель преломления показывает, во сколько раз скорость распространения света в первой среде больше, чем во второй:
Среда, у которой абсолютный показатель преломления больше, является оптически более плотной средой.
Среда, у которой абсолютный показатель преломления меньше, является оптически менее плотной средой.
Следствия закона преломления света
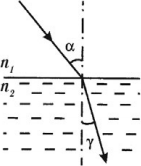
- Если свет падает из оптически менее плотной среды в оптически более плотную, то угол падения больше угла преломления:
- Если свет падает из оптически более плотной среды в оптически менее плотную, то угол падения меньше угла преломления:
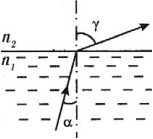
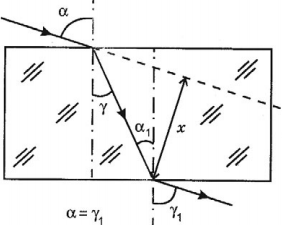
Если луч падает на плоско параллельную пластину, изготовленную из оптически более плотного вещества, чем окружающая среда, то луч не изменяет своего направления, а лишь смещается на некоторое расстояние.
( x ) – смещение луча от первоначального направления:
где ( d ) – толщина пластины.
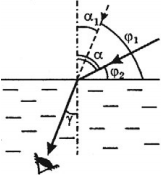
Важно!
Если в условии задачи говорится, что «кажется, что луч падает под углом ( varphi_1 ) к поверхности воды», то имеют в виду не кажущийся угол падения ( alpha_1 ), а угол между кажущимся падающим лучом и поверхностью воды ( varphi_1 ).
Полное внутреннее отражение
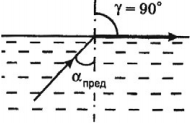
Если свет падает из оптически более плотной среды в оптически менее плотную среду, то с увеличением угла падения увеличивается угол преломления. При некотором значении угла падения угол преломления становится равным 90°. Преломленный луч будет скользить по поверхности раздела двух сред.
Предельный угол полного отражения – это угол падения, при котором угол преломления становится равным 90°:
Если вторая среда – воздух, ( n_2 ) = 1, то ( sinalpha_{пр.}=frac{1}{n_1}. ).
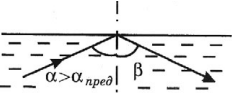
При дальнейшем увеличении угла падения угол преломления тоже увеличивается и наблюдается только отражение света. Это явление называется полным отражением света.
Применение явления полного внутреннего отражения
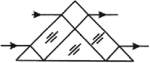
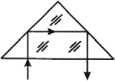
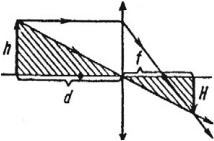
Треугольная призма – прозрачное тело, ограниченное с трех сторон плоскими поверхностями так, что линии их пересечения взаимно параллельны.
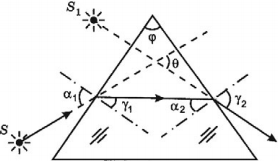
Если призма изготовлена из оптически более плотного вещества, чем окружающая среда, то луч, дважды преломляясь, отклоняется к основанию призмы, а мнимое изображение источника света смещается к вершине призмы.
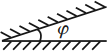
Преломляющий угол призмы – это угол, лежащий против основания.
Угол отклонения луча призмой – это угол между направлениями падающего на призму и вышедшего из призмы лучей.
( varphi ) – преломляющий угол,
( theta ) – угол отклонения луча призмой.
Важно!
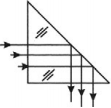
С помощью треугольной равнобедренной призмы с преломляющим углом 90° можно:
- повернуть луч на 90° (поворотная призма, используется в перископах);
- изменить направление луча на 180° (оборотная призма, используется в биноклях);
- изменить относительное расположение лучей.
Линзы. Оптическая сила линзы
Линза – это прозрачное тело, ограниченное двумя сферическими или криволинейными поверхностями, одна из которых может быть плоской.
Тонкая линза – физическая модель линзы, в которой ее толщиной можно пренебречь по сравнению с диаметром линзы.
Классификация линз
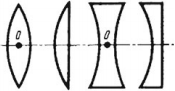
1. По форме:
- выпуклые – это линзы, у которых средняя часть толще, чем края;
- вогнутые – это линзы, у которых края толще, чем средняя часть.
2. По оптическим свойствам:
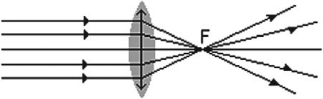
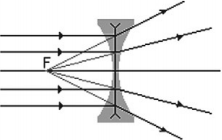
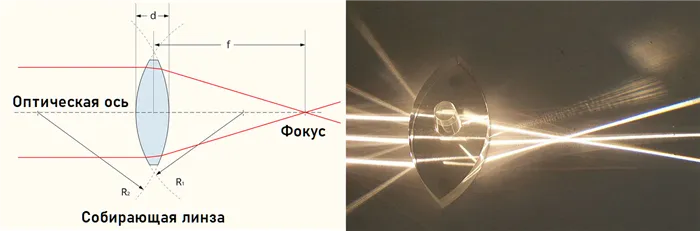
- собирающие – это линзы, после прохождения которых параллельный пучок лучей собирается в одной точке;
- рассеивающие – это линзы, после прохождения которых параллельный пучок лучей рассеивается.
Условные обозначения:
Величины, характеризующие линзу
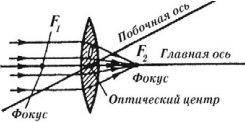
Главная оптическая ось – это прямая, проходящая через центры сферических поверхностей линзы.
Оптический центр линзы – это точка пересечения главной оптической оси с линзой, проходя через которую луч не изменяет своего направления.
Побочная оптическая ось – это любая прямая, проходящая через оптический центр линзы под произвольным углом к главной оптической оси.
Фокус линзы – это точка, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси.
Обозначение – ( F ).
Фокусное расстояние – это расстояние от оптического центра линзы до ее фокуса. Обозначение – ( F ), единица измерения – м.
Фокальная плоскость – это плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
Побочный фокус – это точка пересечения побочной оптической оси с фокальной плоскостью.
Оптическая сила линзы – это величина, обратная фокусному расстоянию.
Обозначение – ( D ), единица измерения – диоптрия (дптр):
1 дптр – это оптическая сила линзы с фокусным расстоянием 1 м.
Важно!
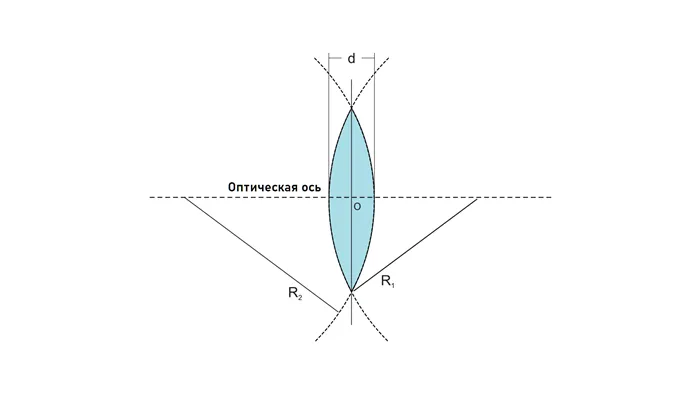
Оптическая сила линзы зависит от показателя преломления линзы и от радиусов кривизны сферических поверхностей, ограничивающих линзу:
где ( n_л ) – показатель преломления линзы, ( n_{ср} ) – показатель преломления среды, ( R_1 ) и ( R_2 ) – радиусы сферических поверхностей.
Если поверхности выпуклые, то ( R_1 ) > 0 и ( R_2 ) > 0, если поверхности вогнутые, то ( R_1 ) < 0 и ( R_2 ) < 0.
Если одна из поверхностей линзы плоская, например первая, то ( R_1toinfty ), а вторая поверхность выпуклая: ( R_2 ) > 0, то
Формула тонкой линзы
где ( F ) – фокусное расстояние линзы, ( d ) – расстояние от предмета до линзы, ( f ) – расстояние от линзы до изображения.
Правило знаков:
- ( F ) > 0, если линза собирающая; ( F ) < 0, если линза рассеивающая;
- ( d ) > 0, если предмет действительный; ( d ) < 0, если предмет мнимый (если на линзу падает сходящийся пучок лучей);
- ( f ) > 0, если изображение действительное; ( f ) < 0, если изображение мнимое.
Линза собирающая, предмет действительный, изображение действительное:
Линза собирающая, предмет действительный, изображение мнимо:
Линза собирающая, предмет мнимый, изображение действительное:
Линза рассеивающая, предмет действительный, изображение мнимое:
Линза рассеивающая, предмет мнимый, изображение мнимое:
Увеличение линзы – это величина, равная отношению линейных размеров изображения к линейным размерам предмета.
Обозначение – ( mathit{Gamma} ), единицы измерения – нет.
где ( H ) – линейный размер изображения, ( h ) – линейный размер предмета.
где ( f ) – расстояние от линзы до изображения, ( d ) – расстояние от предмета до линзы.
Важно!
При расчете увеличения линзы знаки ( f ) и ( d ) не учитываются.
Построение изображений в линзах
Для построения изображения в линзах следует помнить:
- луч, идущий вдоль главной оптической оси линзы, не преломляется;
- луч, проходящий через оптический центр линзы, не преломляется;
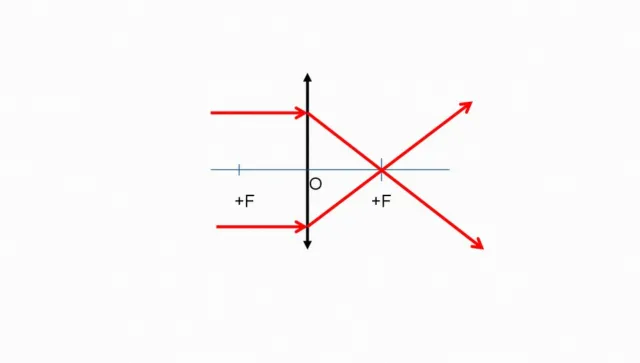
- луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
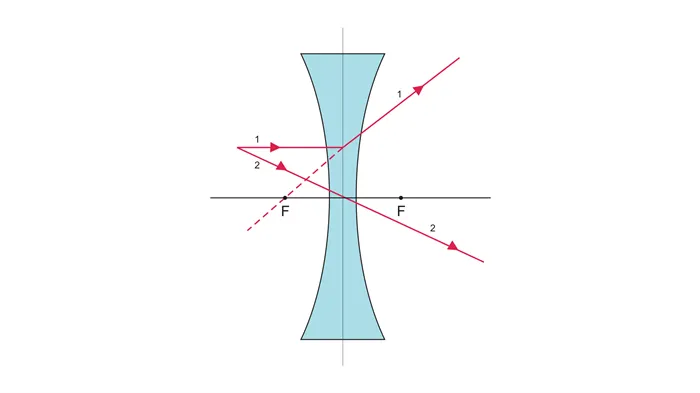
- луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
- луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
- произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
- произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.
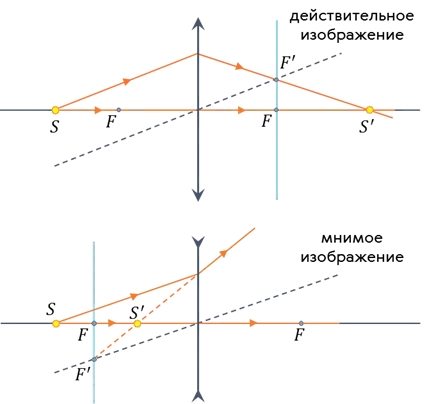
Изображение, даваемое тонкой линзой, может быть действительным или мнимым.
Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.
Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.
Построение изображений точки, даваемых собирающей линзой
- Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.
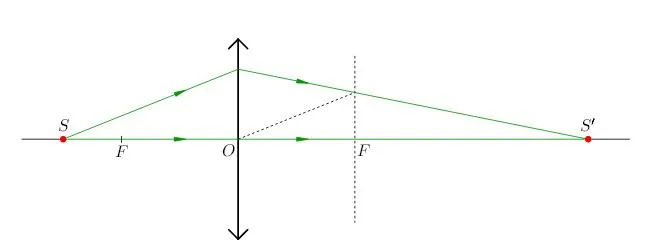
- Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.
- Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.
- Если точка находится в фокусе линзы, то его изображение находится в бесконечности.
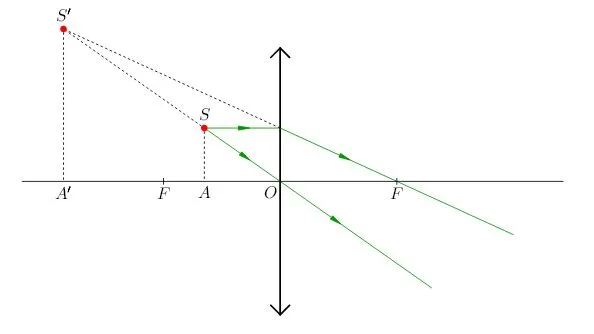
- Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.
Построение изображений предмета, даваемых собирающей линзой
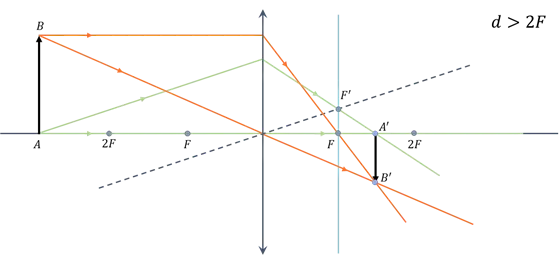
- Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.
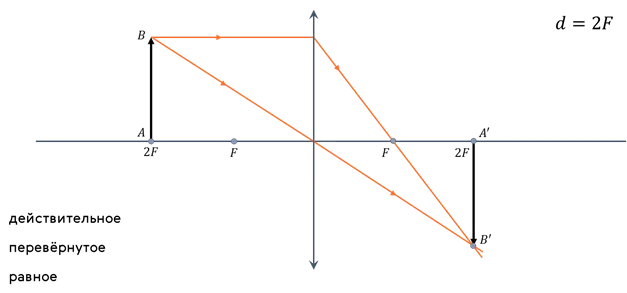
- Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.
- Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.
- Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.
- Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.
Построение изображений точки, даваемых рассеивающей линзой
В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.
Построение изображений предмета, даваемых рассеивающей линзой
Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.
Важно!
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние. Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.
При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.
Оптические приборы. Глаз как оптическая система
Оптические приборы – это устройства, предназначенные для получения на экране, светочувствительных пленках, фотопленках и в глазу изображений различных предметов.
Лупа – это короткофокусная двояковыпуклая линза, предназначенная для относительно небольшого увеличения изображения.
Увеличение лупы рассчитывается по формуле:
где ( d_0 ) – расстояние наилучшего зрения, ( d_0 ) = 0,25 м.
Для получения увеличенного изображения предмет помещают перед линзой на расстоянии немного меньше фокусного. Изображение получается мнимым.
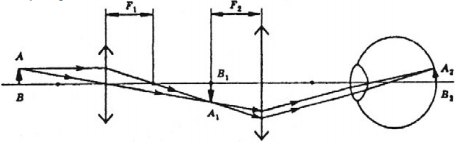
Микроскоп – это оптический прибор, предназначенный для рассматривания очень мелких предметов под большим углом зрения.
Микроскоп состоит из двух собирающих линз – короткофокусного объектива и длиннофокусного окуляра, расстояние между которыми может изменяться:
где ( F_1 ) – фокусное расстояние объектива; ( F_2 ) – фокусное расстояние окуляра.
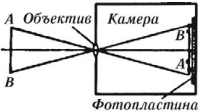
Фотоаппарат – прибор, предназначенный для получения действительных, уменьшенных, перевернутых изображений предметов на фотопленке.
Предметы могут находиться на разных расстояниях.
Мультимедийный проектор – оптическое устройство, с помощью которого на экране получают действительное, увеличенное изображение, снятое с источника видеосигнала.
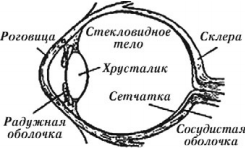
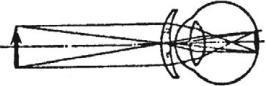
Человеческий глаз – оптическая система, подобная фотоаппарату.
Зрачок регулирует доступ света в глаз. Диаметр зрачка уменьшается при ярком освещении и увеличивается при слабом.
Хрусталик имеет форму двояковыпуклой линзы с показателем преломления 1,41. Он может изменять свою форму, в результате чего меняется его фокусное расстояние. При рассмотрении близких предметов хрусталик становится более выпуклым, при рассмотрении удаленных предметов – более плоским.
На сетчатке глаза образуется действительное, уменьшенное, перевернутое изображение предмета. Благодаря большому количеству нервных окончаний, находящихся на сетчатке, их раздражение передается в мозг и вызывает зрительные ощущения.
Зрение двумя глазами позволяет видеть предмет с разных сторон, т. е. осуществлять объемное зрение.
Если смотреть на предмет одним глазом, то, начиная с 10 м, он будет казаться плоским, если смотреть на предмет двумя глазами, то это расстояние увеличивается до 500 м.
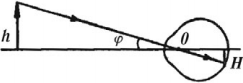
Угол зрения – это угол, образованный лучами, идущими от краев предмета в оптический центр глаза.
( varphi ) – угол зрения.
Аккомодация глаза – это свойство глаза, обеспечивающее четкое восприятие равноудаленных предметов путем изменения фокусного расстояния оптической системы.
Предел аккомодации – от ( infty ) до 10 см.
Расстояние наилучшего зрения – это наименьшее расстояние, с которого глаз может без особого напряжения рассматривать предметы:
Дефекты зрения
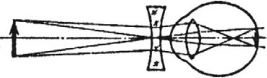
- Близорукость – это дефект оптической системы глаза, при котором ее фокус находится перед сетчаткой. Близорукий глаз плохо видит отдаленные предметы.
- Дальнозоркость – это дефект оптической системы глаза, при котором ее фокус находится за сетчаткой. Дальнозоркий глаз плохо видит близкие предметы.
Очки – это простейший прибор для коррекции оптических недостатков зрения.
Близорукость исправляют с помощью рассеивающих линз.
Дальнозоркость исправляют с помощью собирающих линз.
Интерференция света
Интерференция света – это явление перераспределения энергии в пространстве, происходящее в результате сложения когерентных волн, вследствие чего в одних местах возникают максимумы, а в других минимумы.
Когерентные волны – это волны, имеющие одинаковую частоту и постоянную во времени разность фаз.
Когерентные волны можно получить от одного источника в результате отражения, преломления или дифракции.
Два независимых источника света не могут быть когерентными, поэтому в опытах с интерференцией света световые пучки от одного источника разделяют на два пучка, заставляют их проходить разные расстояния, а потом соединяют.
Когерентными могут быть:
- волны, одна из которых падает на экран непосредственно от источника света, а другая создается его отражением в зеркале (зеркало Ллойда);
- волны, образованные отражением одной и той же волны от двух сдвинутых относительно друг друга поверхностей (тонкие пленки);
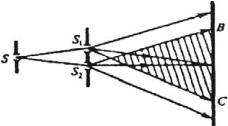
- волны, падающие от точечного источника на непрозрачную преграду с двумя узкими щелями, которые разделяют исходный пучок света на два когерентных пучка (опыт Юнга).
Интерференционная картина представляет собой чередование светлых (цветных) и темных полос.
Источником когерентных волн является лазер.
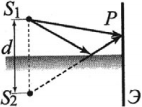
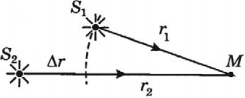
Геометрическая разность хода волн – это разность путей волн от двух когерентных источников ( S_1 ) и ( S_2 ) до точки пространства ( M ), в которой наблюдается интерференция.
Обозначение – ( Delta r ), единица измерения в СИ – м.
Условие максимума интерференции
Если геометрическая разность хода содержит целое число длин волн или четное число длин полуволн, то в месте их наложения друг на друга наблюдается усиление света – максимум:
где ( k ) = 0; 1; 2; 3… – порядок интерференционного максимума.
Условие минимума интерференции
Если геометрическая разность хода содержит нечетное число длин полуволн, то в месте их наложения друг на друга наблюдается ослабление света – минимум:
где ( k ) = 0; 1; 2; 3… – порядок интерференционного минимума.
Если свет распространяется в прозрачной среде с показателем преломления ( n ), то применяют понятие оптической разности хода.
Оптическая разность хода – это величина, равная произведению показателя преломления и геометрической разности хода волн.
Обозначение – ( Delta ), единица измерения в СИ – м.
Интерференция в тонких пленках
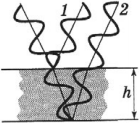
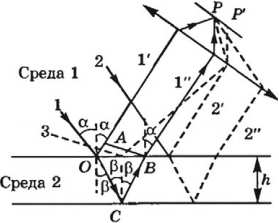
Наблюдаемое в природе радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах) объясняется интерференцией света, возникающей в результате отражения света от передней и задней поверхностей пленки. На тонкую прозрачную пленку толщиной ( h ) падает световая волна, ограниченная лучами 1 и 2. В точке О свет частично отразится от верхней поверхности пленки (волна 1′), а частично преломится и отразится от задней ее поверхности в точке С, преломившись в точке В, выйдет в воздух параллельно волне 1′. Волны 1′ и 1″ когерентны. (То же самое справедливо и для луча 2.)
Если на пути этих лучей поставить собирающую линзу, то они будут накладываться в ее фокальной плоскости и давать интерференционную картину. ( То же самое справедливо и для луча 2.)
Максимум освещенности поверхности тонкой пленки в отраженном свете:
где ( Delta=2kfrac{lambda}{2} ) – оптическая разность хода световых волн при отражении от верхней и нижней поверхности, ( k ) = 1; 2; 3… – целое число длин полуволн, укладывающихся в этой разности хода, ( beta ) – угол преломления.
Минимум освещенности поверхности тонкой пленки в отраженном свете:
Максимум освещенности поверхности тонкой пленки в проходящем свете:
Минимум освещенности поверхности тонкой пленки в проходящем свете:
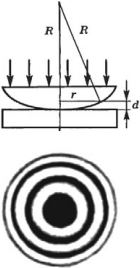
Примером интерференции являются кольца Ньютона, которые наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Воздушная прослойка постепенно утолщается от точки соприкосновения линзы к краям. Отраженные от верхней и нижней границ воздушной прослойки световые волны интерферируют между собой. При этом получается следующая картина: в точке соприкосновения наблюдается черное пятно, окруженное рядом концентрических светлых и темных колец убывающей ширины.
Радиус светлого кольца Ньютона в отраженном свете:
где ( R ) – радиус кривизны линзы, ( k ) – номер кольца, считая от центра интерференционной картины.
Радиус темного кольца Ньютона в отраженном свете:
Радиус светлого кольца Ньютона в проходящем свете:
Радиус темного кольца Ньютона в проходящем свете:
Важно!
При решении задач следует учитывать, в каком свете наблюдается интерференция: в отраженном или проходящем.
Использование интерференции света
- Интерферометры – это приборы, которые контролируют качество обработки поверхностей зеркал, точность изготовления деталей оптических инструментов и измерительных приборов.
- Просветление оптики – на поверхность линз наносят тонкую пленку с показателем преломления меньше, чем показатель преломления стекла. Подбирая толщину пленки и величину показателя преломления, добиваются «гашения отраженных волн», вследствие чего возрастает интенсивность света, пропускаемого линзой.
Дифракция света
Дифракция света – это явление отклонения волны от прямолинейного распространения при прохождении через малые отверстия и огибании волной малых препятствий.
Наилучшее условие для наблюдения дифракции создается, когда размеры отверстий или препятствий – порядка длины волны. Чтобы определить распределение интенсивности световой волны, распространяющейся в среде с неоднородностями, используют принцип Гюйгенса–Френеля.
Принцип Гюйгенса–Френеля
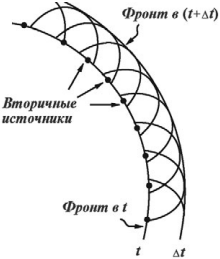
Каждая точка фронта волны является источником вторичных волн, которые интерферируют между собой. Поверхность, касательная ко всем вторичным волнам, представляет новое положение фронта волны в следующий момент времени.
Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой, поэтому амплитуда и фаза волны в любой точке пространства – это результат интерференции волн, излучаемых вторичными источниками.
Дифракционная решетка
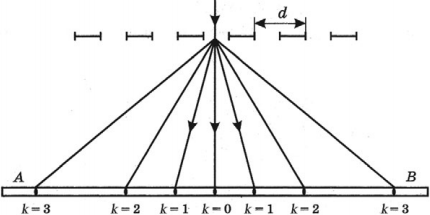
Дифракционная решетка – это оптический прибор, предназначенный для наблюдения дифракции света.
Дифракционная решетка представляет собой систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
Дифракционную решетку применяют для разложения света в спектр и измерения длин световых волн.
Период решетки – это величина, равная сумме ширины прозрачной и непрозрачной полос решетки.
Обозначение – ( d ), единица измерения в СИ – м.
где ( a ) – ширина прозрачной полосы; ( b ) – ширина непрозрачной полосы.
Если решетка регулярна, т. е. ее прозрачные и непрозрачные полосы имеют одинаковую ширину, то период решетки можно рассчитать, разделив ее длину на число штрихов:
где ( l ) – длина решетки, ( N ) – число штрихов.
Формула дифракционной решетки
где ( d ) – период решетки; ( varphi ) – угол дифракции; ( k ) = 0; 1; 2… – порядок максимума, считая от центрального ( k ) = 0 и расположенного напротив центра решетки; ( lambda ) – длина волны, падающей на решетку нормально к ней.
Если дифракционная решетка освещается белым светом, то при ( k ) ≠ 0 разным длинам волн будут соответствовать разные дифракционные углы. Поэтому положение главных максимумов ненулевого порядка будет различным. Центральный максимум (( k ) = 0) остается белым, т. к. при ( k ) = 0 для всех длин волн ( varphi ) = 0, т. е. положение главного максимума для всех длин волн одинаково. Все остальные максимумы имеют вид радужных полос, называемых дифракционными спектрами первого порядка (( k ) = 1), второго порядка (( k ) = 2) и т. д. Ближе к центральному максимуму находится фиолетовый край спектра, дальше всего – красный, т. к. ( lambda_{фиол}<lambda_{кр} ), то и ( varphi_{фиол}<varphi_{кр} ).
Важно!
Поскольку углы, под которыми наблюдаются максимумы первого и второго порядка, не превышают 5°, можно вместо синусов углов использовать их тангенсы.
Дисперсия света
Дисперсия света – это зависимость показателя преломления среды от длины волны (частоты) падающего на вещество света.
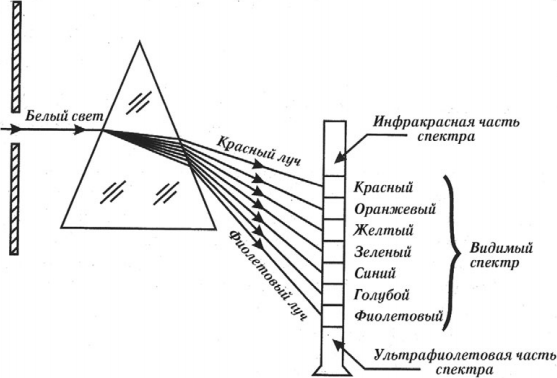
Опыт Ньютона (1672)
Из-за дисперсии световые волны с различной длиной волны поразному преломляются веществом, что приводит к разложению белого света на цветные монохроматические лучи – спектр.
Для лучей света различной цветности показатели преломления данного вещества различны, т. к. различны скорости распространения электромагнитных волн, у которых разная длина волны. Луч красного света преломляется меньше из-за того, что красный свет имеет в веществе наибольшую скорость, а луч фиолетового цвета преломляется больше, так как скорость для фиолетового цвета наименьшая. Это объясняется особенностями взаимодействия этих волн с электронами, входящими в состав атомов и молекул вещества среды, где они движутся.
Дисперсией света объясняется такое природное явление, как радуга.
Основные формулы по теме «Оптика»
Оптика
3 (60.87%) 115 votes
Тема .
№29 Электродинамика. Квантовая физика (Расчетная задача высокого уровня сложности)
.
04
Скорость изображения в различных оптических системах
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
№29 электродинамика. квантовая физика (расчетная задача высокого уровня сложности)
Решаем задачи
Показать ответ и решение
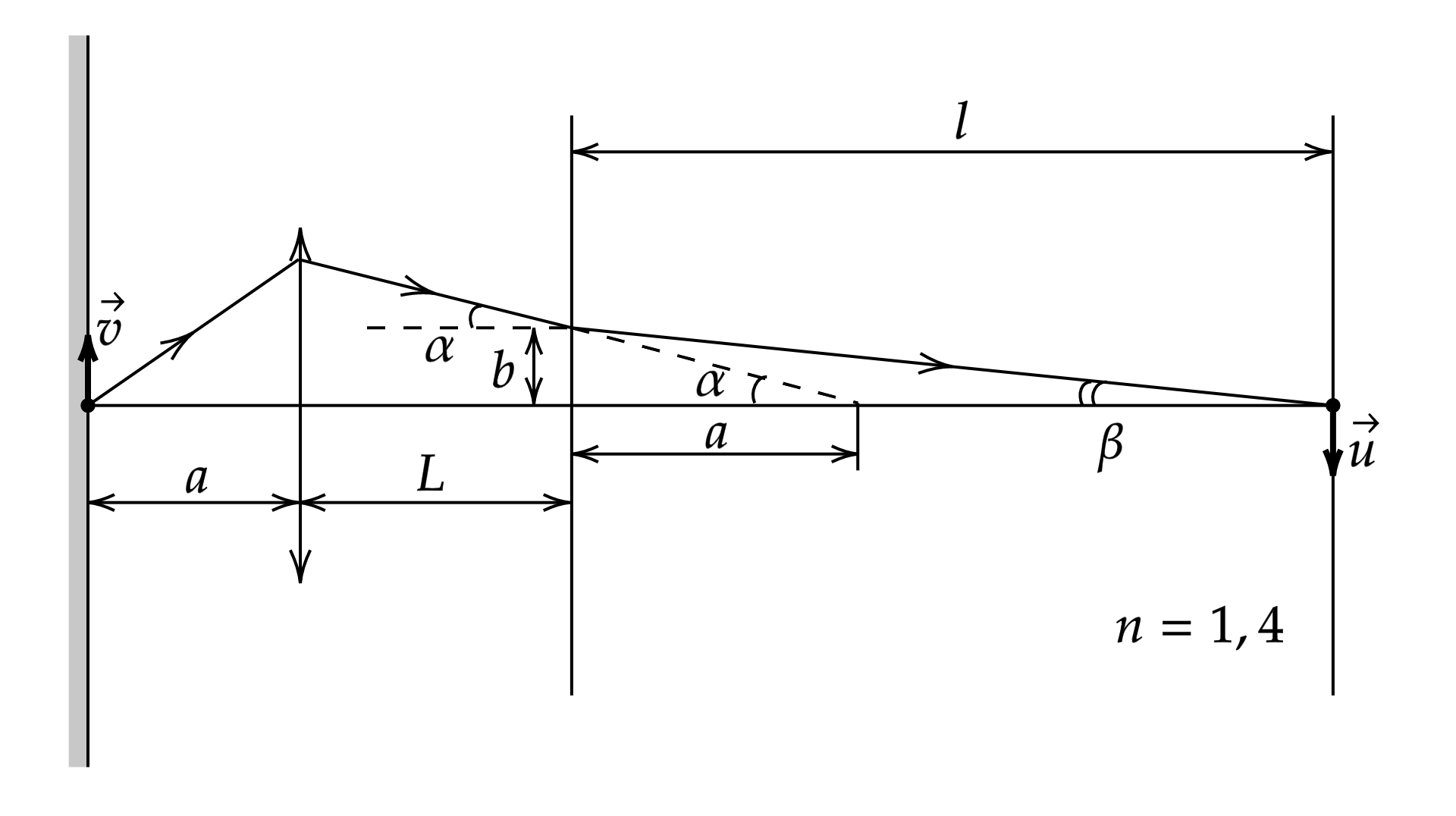
Из тригонометрии , так как углы малые, то
. Тогда
отношение
По закону Снеллиуса или с учетом малости углов
Тогда см – расстояние от линзы до изображения, если бы система состояла только
из линзы.
Запишем формулу тонкой линзы
Поперечное увеличение
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: Сделан поясняющий рисунок,
записан закон Снеллиуса, записана формула тонкой линзы)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
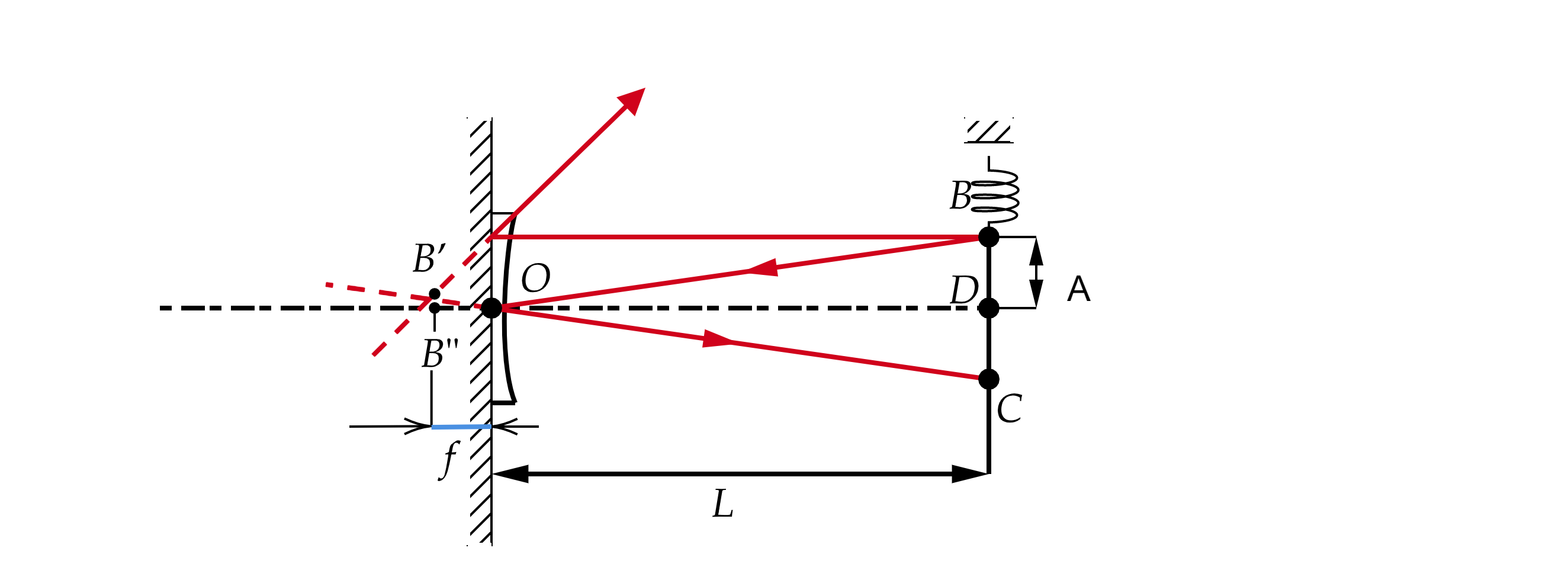
1) Изобразим ход лучей для момента, когда груз находится в максимальном удалении от главной
оптической оси (точка ). Изображение
получается после двойного прохождения лучами линзы и
отражения в зеркале (см. рис.).
Тогда по формуле тонкой линзы:
Двойка в правой части возникает из-за двойного прохождения лучами линзы. Откуда
2) На рисунке расстояние от грузика до главной оптической оси равно , а расстояние от
изображения до главной оптической оси равно
. ИЗ подобия треугольников
и
можно найти:
Пусть , тогда
Возьмём производную по времени от :
Грузик колеблется с циклической частотой:
При этом колебания описываются уравнением
где – начальная фаза колебаний (в данном случае
). Взяв производную от
получим
где – максимальная скорость грузика. В момент прохождения главной оптической оси
скорость изображения грузика максимальна, значит, можно найти
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сделан поясняющий рисунок,
записана формула токной линзы, записано уравнение колебаний, записана формула циклической
частоты)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
1) Запишем формулу тонкой линзы при отсутствии зеркала:
где – расстояние от линзы до действительного изображения
.
Откуда
2) Пусть см – расстояние между зеркалом и линзы. Так как
, то
является
мнимым предметом для зеркала. Для того, чтобы на экране наблюдалось резкое изображение должно
выполняться равенство:
откуда искомая величина
3) Найдём увеличение линзы:
Скорости изображения, полученного в линзе, и источника
связаны формулой:
При этом зеркало не меняется скорость, следовательно, максимальная скорость изображения на
экране:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
тонкой линзы, записана формула увеличения, сказано при каком условии изображение будет
резким)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Груз на пружине совершает гармонические колебания перпендикулярно главной оптической оси
собирающей линзы с оптической силой 5 дптр (см. рисунок). С помощью этой линзы получено чёткое
изображение груза на экране, находящемся на расстоянии 0,5 м от линзы. Максимальная скорость
изображения равна 1 м/с. Определите максимальную скорость самого груза, считая груз материальной
точкой.
Показать ответ и решение
Пусть расстояние от линзы до предмета , расстояние от линзы до изображения
, увеличение линзы
,
– максимальное значение скорости груза,
– максимальное значение скорости
изображения.
Груз и изображение груза совершают колебания с одинаковой циклической частотой . Так как
колебания груза описываются уравнением:
где – амплитуда,
– начальная фаза.
Отсюда скорость описывается уравнением:
Тогда Если амплитуда колебаний груза равна , а амплитуда колебаний изображения
, то по
формуле увеличения:
Отсюда:
Запишем также формулу тонкой линзы:
где – оптическая сила линзы.
Отсюда:
Тогда объединяя (1) – (3), получим:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формулы тонкой
линзы, связи фокусного расстояния и оптической силы линзы, увеличения, даваемого линзой,
формулы кинематического описания гармонического движения для координаты и скорости
(или формула связи амплитуды колебания координаты с амплитудой колебания скорости)
)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Висящий на пружине груз совершает вертикальные колебания, двигаясь перпендикулярно главной
оптической оси линзы с фокусным расстоянием см. На экране, который можно перемещать,
получено изображение груза. При этом максимальная скорость изображения оказалась в 8 раз больше
максимальной скорости груза.
1) Найдите расстояние между грузом и линзой.
2) Найдите фокусное расстояние собирающей линзы, которую надо поместить вплотную к первой
линзе, чтобы максимальная скорость изображения уменьшилась в 4 раза по сравнению с предыдущей.
(«Физтех», 2012)
Показать ответ и решение
1) Запишем формулу тонкой линзы:
где – расстояние от линзы до предмета,
– расстояние от линзы до изображения.
Увеличение равно:
где – скорость изображения,
– скорость предмета.
Так как максимальная скорость изображения оказалась в 8 раз больше максимальной скорости груза,
то , отсюда
Тогда из формулы тонкой линзы:
2) Если расстоянием между линзами можно пренебречь, то оптическая сила системы из двух линз
равна сумме оптических сил линз, то есть
где – оптическая сила первой линзы,
– оптическая сила второй линзы.
Запишем формулу тонкой линзы:
где – расстояние от линзы до предмета,
– расстояние от линзы до изображения.
Увеличение равно:
где – скорость изображения,
– скорость предмета.
Так как максимальная скорость изображения уменьшилась в 4 раза по сравнению с предыдущей, то
максимальная скорость изображения оказалась в 2 раз больше максимальной скорости груза, то есть
, отсюда
Тогда из формулы тонкой линзы:
Отсюда
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения, записана формула оптической силы линзы)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Груз массой 0,1 кг, прикрепленный к пружине жесткостью 0,4 Н/м, совершает гармонические колебания
с амплитудой 0,1 м. При помощи собирающей линзы с фокусным расстоянием 0,2 м изображение
колеблющегося груза проецируется на экран, расположенный на расстоянии 0,5 м от линзы. Главная
оптическая ось линзы перпендикулярна траектории груза и плоскости экрана. Определите
максимальную скорость изображения груза на экране.
Сборник задач «1000 задач»
Показать ответ и решение
При колебаниях выполняется закон сохранения энергии, из которого можно выразить максимальную
скорость груза:
где – амплитуда колебания.
Максимальная скорость на экране изображения расположенном на расстоянии
от линзы,
пропорциональна скорости груза, движущегося на расстоянии от плоскости тонкой линзы и может
быть найдена из подобия треугольников:
По формуле тонкой линзы можно найти
Тогда
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: закон сохранения энергии для
гармонических колебаний, записана формула тонкой линзы, найдено отношение скоростей
изображения и источника)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью
м/с движется точечный источник света. Расстояние между плоскостями см. Центр окружности
находится на главной оптической оси линзы. Фокусное расстояние линзы = 10 см. Найдите скорость
движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в
линзе.
Демоверсия 2019
Показать ответ и решение
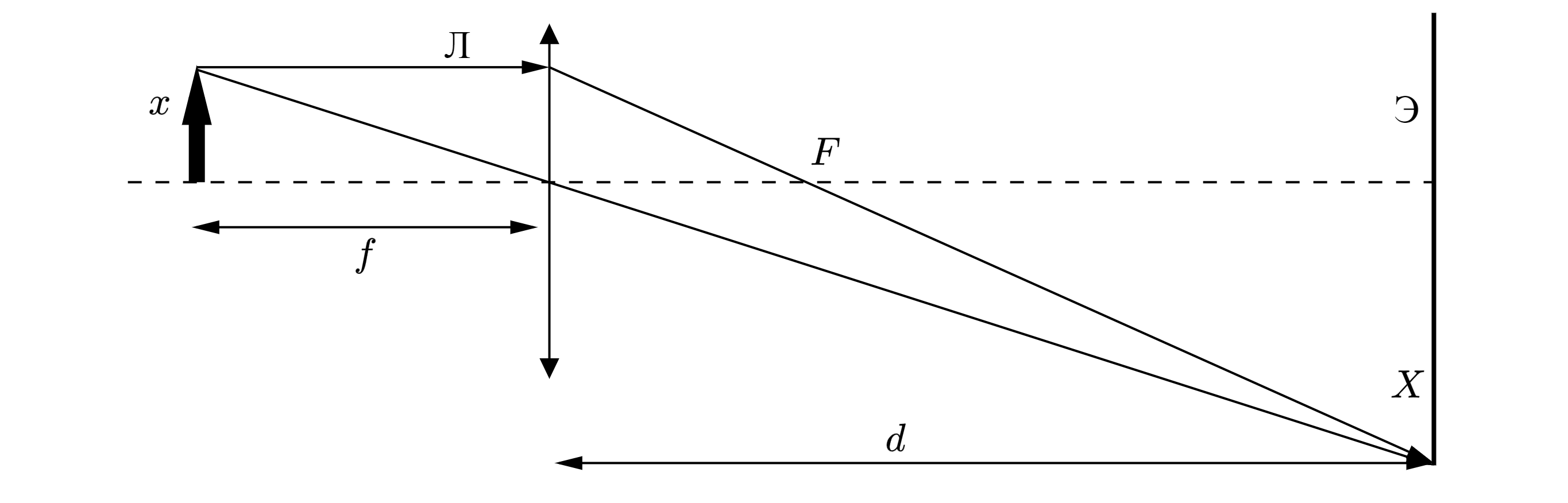
Сделаем рисунок:
Согласно формуле тонкой линзы, расстояние от предмета до линзы , расстояние от линзы до
изображения и фокусное расстояние
связаны соотношением
Отсюда расстояние от линзы до изображения составляет
Линейное увеличение для изображения предмета тонкой линзой равно
где – расстояние от главной оптической оси до изображения источника света,
– расстояние от
главной оптической оси до источника света.
Изображение и источник света вращаются относительно главной оптической оси на разных расстояниях,
но с одним и тем же периодом. При движении по окружности скорость может быть найдена
как
Запишем отношение скоростей изображения и источника света и выразим отсюда скорость
изображения
Подставим числа
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула тонкой линзы,
формула увеличения, даваемого линзой, доказано равенство угловых скоростей движения предмета и
его изображения, записаны формулы для угловой и линейной скоростей движения точки, сделан
верный чертеж с указанием хода лучей)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник, находящийся на главной оптической оси собирающей линзы на расстоянии от нее, в
полтора раза большем фокусного, начинает смещаться со скоростью 4 мм/с перпендикулярно оси. С
какой скоростью движется изображение источника?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– растояние от изображения до линзы
– расстояние от предмета до оси
– расстояние от изображения до оси
Возьмем производную по времени
где – скорость изображения,
– скорость источника
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник находится на главной оптической оси собирающей линзы с фокусным
расстоянием 6 см на расстоянии 8 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в
направлении, перпендикулярном оптической оси. С какой скоростью движется изображение
источника?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Перейдем в систему отсчета, связанную с линзой. В ней источник движется со скоростью 3
мм/с.
Увеличение линзы равно:
– скорость предмета относительно линзы
– скорость изображения источника в системе отсчета, связанной с линзой
Чтобы узнать скорость изображения, надо перейти обратно в неподвижную систему отсчета, для
этого необходимо:
Критерии оценки
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула тонкой
линзы, записана формула увеличения)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Точечный источник движется со скоростью 2 мм/с вдоль главной оптической оси собирающей линзы с
фокусным расстоянием 8 см. С какой скоростью движется изображение источника в тот момент, когда
источник находится от линзы на расстоянии 10 см?
Показать ответ и решение
Формула тонкой линзы для собирающей линзы:
где – фокусное расстояние,
– расстояние от предмета до линзы
– расстояние от изображения до линзы
Возьмем производную по времени
Заметим, что – скорость предмета,
– скорость изображения.
Тонкие линзы. Ход лучей.
-
Понятие тонкой линзы.
-
Оптический центр и фокальная плоскость.
-
Ход луча через оптический центр.
-
Ход лучей в собирающей линзе.
-
Ход лучей в рассеивающей линзе.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: линзы, оптическая сила линзы
Взгляните ещё раз на рисунки линз из предыдущего листка: эти линзы обладают заметной толщиной и существенной кривизной своих сферических границ. Мы намеренно рисовали такие линзы — чтобы основные закономерности хода световых лучей проявились как можно более чётко.
к оглавлению ▴
Понятие тонкой линзы.
Теперь, когда эти закономерности достаточно ясны, мы рассмотрим очень полезную идеализацию, которая называется тонкой линзой.
В качестве примера на рис. 1 приведена двояковыпуклая линза; точки и
являются центрами её сферических поверхностей,
и
— радиусы кривизны этих поверхностей.
— главная оптическая ось линзы.
 |
| Рис. 1. К определению тонкой линзы |
Так вот, линза считается тонкой, если её толщина очень мала. Нужно, правда, уточнить: мала по сравнению с чем?
Во-первых, предполагается, что и
. Тогда поверхности линзы хоть и будут выпуклыми, но могут восприниматься как «почти плоские». Этот факт нам очень скоро пригодится.
Во-вторых, , где
— характерное расстояние от линзы до интересующего нас предмета. Собственно, лишь в таком случае мы и
сможем корректно говорить о «расстоянии от предмета до линзы», не уточняя, до какой именно точки линзы берётся это самое расстояние.
Мы дали определение тонкой линзы, имея в виду двояковыпуклую линзу на рис. 1. Это определение без каких-либо изменений переносится на все остальные виды линз. Итак: линза является тонкой, если толщина линзы много меньше радиусов кривизны её сферических границ и расстояния от линзы до предмета.
Условное обозначение тонкой собирающей линзы показано на рис. 2.
 |
| Рис. 2. Обозначение тонкой собирающей линзы |
Условное обозначение тонкой рассеивающей линзы показано на рис. 3.
 |
| Рис. 3. Обозначение тонкой рассеивающей линзы |
В каждом случае прямая — это главная оптическая ось линзы, а сами точки
— её
фокусы. Оба фокуса тонкой линзы расположены симметрично относительно линзы.
к оглавлению ▴
Оптический центр и фокальная плоскость.
Точки и
, обозначенные на рис. 1, у тонкой линзы фактически сливаются в одну точку. Это точка
на рис. 2 и 3, называемая оптическим центром линзы. Оптический центр находится на Пересечении линзы с её главной оптической осью.
Расстояние от оптического центра до фокуса называется фокусным расстоянием линзы. Мы будем обозначать фокусное расстояние буквой
. Величина
, обратная фокусному расстоянию, есть оптическая сила — линзы:
.
Оптическая сила измеряется в диоптриях (дптр). Так, если фокусное расстояние линзы равно 25 см, то её оптическая сила:
дптр
Продолжаем вводить новые понятия. Всякая прямая, проходящая через оптический центр линзы и отличная от главной оптической оси, называется побочной оптической осью . На рис. 4 изображена побочная оптическая ось — прямая .
 |
| Рис. 4. Побочная оптическая ось, фокальная плоскость и побочный фокус |
Плоскость , проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость, таким образом, параллельна плоскости линзы. Имея два фокуса, линза соответственно имеет и две фокальных плоскости, расположенных симметрично относительно линзы.
Точка , в которой побочная оптическая ось пересекает фокальную плоскость, называется побочным фокусом. Собственно, каждая точка фокальной плоскости (кроме
) есть побочный фокус — мы ведь всегда сможем провести побочную оптическую ось, соединив данную точку с оптическим центром линзы. А сама точка
— фокус линзы — в связи с этим называется ещё главным фокусом.
То, что на рис. 4 изображена собирающая линза, никакой роли не играет. Понятия побочной оптической оси, фокальной плоскости и побочного фокуса совершенно аналогично определяются и для рассеивающей линзы — с заменой на рис. 4 собирающей линзы на рассеивающую.
Теперь мы переходим к рассмотрению хода лучей в тонких линзах. Мы будем предполагать, что лучи являются параксиальными, то есть образуют достаточно малые углы с главной оптической осью. Если параксиальные лучи исходят из одной точки, то после прохождения линзы преломлённые лучи или их продолжения также пересекаются в одной точке. Поэтому изображения предметов, даваемые линзой, в параксиальных лучах получаются весьма чёткими.
к оглавлению ▴
Ход луча через оптический центр.
Как мы знаем из предыдущего раздела, луч, идущий вдоль главной оптической оси, не преломляется. В случае тонкой линзы оказывается, что луч, идущий вдоль побочной оптической оси, также не преломляется!
Объяснить это можно следующим образом. Вблизи оптического центра обе поверхности линзы неотличимы от параллельных плоскостей, и луч в данном случае идёт как будто через плоскопараллельную стеклянную пластинку (рис. 5).
 |
| Рис. 5. Ход луча через оптический центр линзы |
Угол преломления луча равен углу падения преломлённого луча
на вторую поверхность. Поэтому второй преломлённый луч
выходит из плоскопараллельной пластинки параллельно падающему лучу
. Плоскопараллельная пластинка лишь смещает луч, не изменяя его направления, и это смещение тем меньше, чем меньше толщина пластинки.
Но для тонкой линзы мы можем считать, что эта толщина равна нулю. Тогда точки фактически сольются в одну точку, и луч
окажется просто продолжением луча
. Вот поэтому и получается, что луч, идущий вдоль побочной оптической оси, не преломляется тонкой линзой (рис. 6).
 |
| Рис. 6. Луч, идущий через оптический центр тонкой линзы, не преломляется |
Это единственное общее свойство собирающих и рассеивающих линз. В остальном ход лучей в них оказывается различным, и дальше нам придётся рассматривать собирающую и рассеивающую линзу по отдельности.
к оглавлению ▴
Ход лучей в собирающей линзе.
Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный главной оптической оси, после прохождения линзы собирается в её главном фокусе (рис. 7).
 |
| Рис. 7. Параллельный пучок собирается в главном фокусе |
Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном фокусе собирающей линзы находится точечный источник света, то на выходе из линзы получится световой пучок, параллельный главной оптической оси (рис. 8).
 |
| Рис. 8. Преломление пучка, идущего из главного фокуса |
Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно, тоже соберётся в фокусе — но в побочном. Этот побочный фокус отвечает тому лучу, который проходит через оптический центр линзы и не преломляется (рис. 9).
 |
| Рис. 9. Параллельный пучок собирается в побочном фокусе |
Теперь мы можем сформулировать правила хода лучей в собирающей линзе. Эти правила вытекают из рисунков 6-9,
1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус (рис. 10).
 |
| Рис. 10. К правилу 2 |
3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч (рис. 11).
 |
| Рис. 11. К правилу 3 |
В частности, если падающий луч проходит через фокус линзы, то после преломления он пойдёт параллельно главной оптической оси.
к оглавлению ▴
Ход лучей в рассеивающей линзе.
Переходим к рассеивающей линзе. Она преобразует пучок света, параллельный главной оптической оси, в расходящийся пучок, как бы выходящий из главного фокуса (рис. 12)
 |
| Рис. 12. Рассеяние параллельного пучка |
Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фокусе позади линзы.
Если параллельный пучок падает на линзу наклонно, то после преломления он также станет расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе , отвечающем тому лучу, который проходит через через оптический центр линзы и не преломляется (рис. 13).
 |
| Рис. 13. Рассеяние наклонного параллельного пучка |
Этот расходящийся пучок создаст у нас иллюзию светящейся точки, расположенной в побочном фокусе за линзой.
Теперь мы готовы сформулировать правила хода лучей в рассеивающей линзе. Эти правила следуют из рисунков 6, 12 и 13.
1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус (рис. 14).
 |
| Рис. 14. К правилу 2 |
3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса (рис. 15).
 |
| Рис. 15. К правилу 3 |
Пользуясь правилами хода лучей 1–3 для собирающей и рассеивающей линзы, мы теперь научимся самому главному — строить изображения предметов, даваемые линзами.
Разберем задачи ЕГЭ по теме: Тонкие линзы.
1. На экране с помощью тонкой линзы получено изображение предмета с пятикратным увеличением. Экран передвинули на 30 см вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получилось изображение с трехкратным увеличением. На сколько пришлось передвинуть предмет относительно первоначального положения?
Дано:
Г₁=5
Г₂=3
а = 30 см = 0,3 м.
Найти:
Δd — ?
Решение.
При решении этой задачи главным является создание модели, которая поясняет изменения в увеличении линзы и позволяет правильно определить перемещение экрана и предмета. На представленных ниже рис.1 и рис.2 выполнены все необходимые построения для двух случаев задачи. Так как увеличение линзы уменьшается, то предмет смещается в сторону двойного фокуса. Именно в этом случае возможно уменьшение изображения, по сравнению с первым случаем.
Особое внимание надо обратить на фразу, что изображение снова стало резким. Это возможно только при выполнении всех соотношений в формуле тонкой линзы
Для каждого случая запишем формулу тонкой линзы и учтем соотношения между d и f через значение увеличения (Г), даваемое линзой.
Г₁
, отсюда
Г₂
, отсюда
Тогда формулы (1) и (2) примут вид:
Остается решить следующую систему из двух уравнений:
Решение этой системы можно провести с подстановкой численных значений.
(м). Тогда
(м)
(м)
(м)
(м).
Ответ: 0,02 м
2. На оси ОХ в точке находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием
см, а в точке
см – тонкой собирающей линзы. Главные оптические ос обеих линз лежат на оси ОХ. На рассеивающую линзу вдоль оси ОХ падает параллельный пучок света из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой
см. Найдите фокусное расстояние собирающей линзы
.
Дано:
см = -0,2 м
см = 0,2 м
см = 0,6 м
Найти:
— ?
Решение
На рисунке представлен ход лучей через систему рассеивающей и собирающей линз. При решении подобных задач необходимо рассматривать отдельно ход лучей сквозь каждую линзу.
Рассмотрим сначала ход лучей через рассеивающую линзу. Для этого воспользуемся формулой тонкой линзы и учтем, что , так как на рассеивающую линзу падает параллельный пучок света из области
. Тогда дробь
и формула примет вид:
Перед стоит знак (-), так как линза рассеивающая и она дает всегда мнимое изображение.
Поэтому (м).
В точке S сформировалось мнимое изображение светового пучка, который падает на собирающую линзу из области
Теперь отдельно рассмотрим собирающую линзу. Для нее расстояние будет равно 0,4 м (согласно рисунку). Применим для собирающей линзы формулу тонкой линзы с учетом
и
. Расстояние
;
(м).
(м) = 20 (см).
Ответ: 20 см.
3. Точечный источник света движется со скоростью v вокруг главной оптической оси собирающей линзы в плоскости, параллельной плоскости линзы на расстоянии d=15 см от линзы. Фокусное расстояние линзы F= 10 cм. Скорость движения изображения точечного источника света V=10 м/с. Найдите скорость движения источника света.
Дано:
d=15 см = 0,15 м
F= 10 см = 0,1 м
V=10 м/с
Найти: v-?
Решение.
Для решения этой задачи воспользуемся формулой тонкой линзы.
Проведем расчет для определения расстояния от линзы до изображения.
(м).
Полученный результат говорит о том, что увеличение линзы Г>1.
Г =
Точечный источник и его изображение будут двигаться с разными линейными скоростями, но в тоже самое время период их обращения, частота обращения и угловые скорости у них будут равными. Радиусы окружностей, которые будут описывать источник света и его изображения, будут отличаться в 2 раза. Радиус окружности изображения R будет превышать радиус окружности источника r в 2 раза или
Воспользуемся формулой равенства периодов обращения.
(м/с)
4. Точечный источник света S расположен на расстоянии 40 cм от оптического центра тонкой собирающей линзы с фокусным расстоянием 0,2 м на её главной оптической оси АВ. На сколько сместиться вдоль прямой АВ изображение источника, если линзу повернуть на угол =30° относительно оси, перпендикулярной плоскости рисунка и проходящей через оптический центр линзы? Сделайте пояснительный чертеж, указав ход лучей в линзе для обоих случаев её расположения.
Дано:
cм = 0,4 м
F = 0,2 м
= 30°
Найти:
— ?
Решение.
Применим формулу тонкой линзы для первого случая.
(м).
Применим формулу тонкой линзы для второго случая.
Здесь необходимо учесть, что (м).
(м).
Изображение источника во втором случае также формируется на прямой АВ. Для нахождения расстояния необходимо
(м).
Таким образом, изображения источников в обоих случаях получились на прямой АВ на расстоянии (м).
Ответ: 0,14 м.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Тонкие линзы. Ход лучей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Как правило, типы тонких линз записываются следующим образом. Сумма инверторов расстояний от объекта до линзы, сумма расстояний от линзы до изображения равна обратной величине фокусного расстояния.
Тонкие линзы. Построение изображений.
Использование кода: изготовление изображений линз, тонкие типы линз.
Правило маршрута лучей света в тонких линзах, сформулированное в предыдущем выпуске, приводит к самому важному утверждению.
Теорема об образе. Если перед линзой находится яркая точка, то после преломления линзы все лучи света (или их продолжение) пересекаются в одном и том же месте.
Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы.
Точка называется образом точки.
Если сами преломленные лучи пересекаются в этой точке, изображение называется действительным. Лучи видны на экране, потому что энергия лучей сосредоточена в этой точке.
Если преломленный луч пересекает точку, но его непрерывность (это происходит, когда преломленный луч отклоняется после линзы) называется иллюзорной. Энергия не концентрируется в точке и поэтому не может быть получена на экране. Фантастические образы появляются благодаря состоянию нашего мозга. Сфокусируйте ветвящиеся лучи на иллюзорном перекрестке и покажите, что видите светлое место на этом перекрестке. Фантастический образ существует только в нашем сознании.
Теорема об изображении служит основой для создания изображений с тонкими линзами. Докажите теорему для аспирированных и диффузных линз.
Собирающая линза: действительное изображение точки.
Сначала рассмотрим изогнутые линзы. Как минимум — расстояние пятна от объектива, фокусное расстояние объектива. Есть два радикально разных случая. И (и промежуточный случай). Мы рассмотрим эти случаи один за другим, каждый из которых описывает характеристики точечного источника и изображение более широкого объекта.
Первый случай:. Прожектор находится дальше от линзы, чем левая фокальная плоскость (рис. 1).
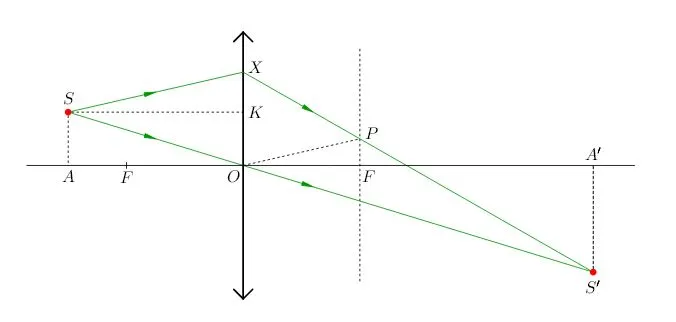 |
| Рис. 1. Случай a>f: действительное изображение точки S |
Радиус, проходящий через зрительный центр, не преломляется. Возьмите любой радиус и постройте точку пересечения преломленного радиуса с радиусом, показав, что положение точки не зависит от выбора радиуса (другими словами, точка одинакова для всех лучей). Таким образом, после пересечения линз преломления в точке и доказательства теоремы об образе все лучи выходят.
Точка находится путем планирования дальнейшего хода радиуса. Мы знаем, как это сделать: проводим визуальную ось, параллельную лучу, в месте ее пересечения с уровнем фокуса падающего фокуса и преломляем луч до разреза в луче.
Теперь мы ищем расстояние от точки до линзы. Расстояние определяется только и, то есть положением источника и свойствами линзы, так что расстояние дается только и не зависит от конкретного луча.
Перпендикулярно главной визуальной оси. Также спроектируйте его параллельно главной зрительной оси, т.е. перпендикулярно линзе. Вы получаете три набора подобных треугольников.
В результате получается следующая цепочка равенств (количество типов над символом равенства указывает на то, что пара одинаковых треугольников приводит к этому равенству).
Однако соотношение (4) переписывается в виде.
Таким образом, существует необходимое расстояние от точки до линзы.
Как видите, это не зависит от выбора балки. Поэтому все радиусы после преломления линзы проходят через точку, которую мы сделали. Эта точка будет истинным изображением источника.
В этом случае доказывается теорема об образе.
Практическая важность теоремы об образах заключается в следующем. Все лучи источника пересекаются после линзы в какой-то точке, поэтому достаточно получить два луча, которые наиболее подходят для построения изображения — его идолов. Какие два?
Если источник находится не на главной зрительной оси, то подходят следующие лучи
— Радиус, проходящий через зрительный центр линзы — без преломления — и радиус, параллельный главной зрительной оси, после прохождения преломления через камин.
Структура изображения с этими лучами показана на рисунке 2.
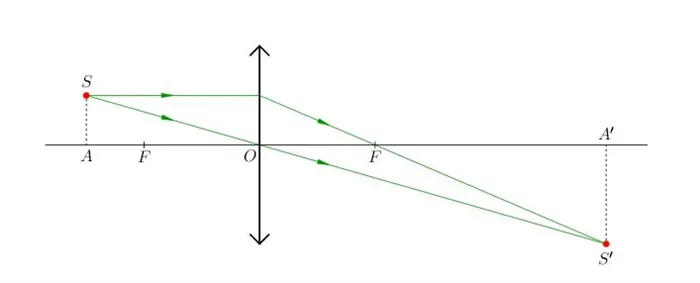 |
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если точка находится на главной визуальной оси, подходит только один радиус, который перемещается вдоль главной визуальной оси. Второй радиус должен быть «неловким» (рис. 3).
Собирающая линза: действительное изображение предмета.
Рассмотрим изображение объекта. Напомним, что мы все еще находимся в этом случае. Можно выделить три характерные ситуации.
1. Изображение объекта является реальным, перевернутым и увеличенным (рис. 4, показан двойной фокус). Тип объектива не является фактором, определяющим, является ли он таковым (почему?) так и есть.
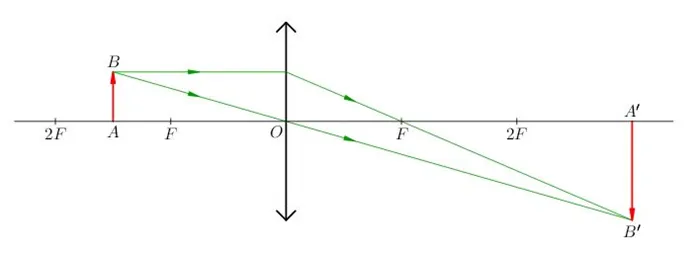 |
| Рис. 4. : изображение действительное, перевёрнутое, увеличенное |
Такая ситуация возникает, например, при включенных фарах на слайдах и фарах в фильмах. Эти визуальные средства дают на экране эффектное изображение того, что происходит в фильме. Если вы когда-либо представляли слайды, то знаете, что для того, чтобы слайд появился на экране, его нужно ввести вверх ногами, а не вверх ногами.
Причина приведения размера изображения к размеру объекта называется линейным расширением линзы и обозначается G- (это заглавная буква греческого «гамма»).
В зависимости от схожести треугольников, в зависимости от
Тип (8) используется во многих задачах, где имеет место линейное увеличение линзы.
2 … В данном случае тип (6) указывает на это. ( Линейное расширение линзы, обусловленное (8), является унитарным. Это означает, что размер изображения равен размеру объекта (рис. 5).
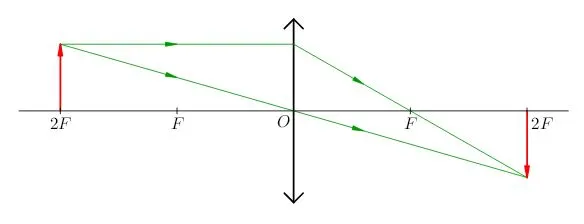 |
| Рис. 5.a=2f: размер изображения равен размеру предмета |
3 … В данном случае тип объектива указывает на то, что (почему?). Линейное увеличение линзы меньше единицы — изображение получается реальным, перевернутым и уменьшенным (рис. 6).
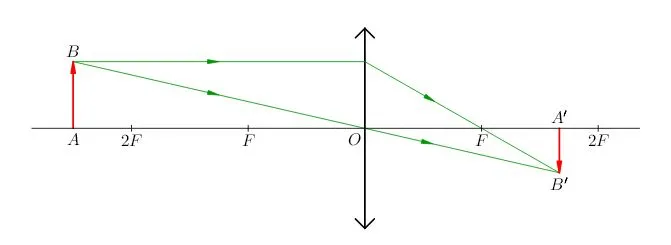 |
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Это общая проблема для многих визуальных приборов. Для изображения удаленных объектов используются камеры, бинокли, телескопы, короче говоря, объективы. Когда объект удаляется от линзы, его холостой размер уменьшается, и он перемещается ближе к фокальной плоскости.
Проверка первого дела завершена. Перейдем ко второму случаю. Он не обладает большой вместимостью.
Линзы являются коллекционными и могут быть разбросаны. Рассеивающие линзы, с другой стороны, тоньше в центральной части, в то время как коллекционные линзы толще в центре, чем по краям.
Построение изображения в линзах
Вы уже знаете, что линза — это прозрачное тело, которое фокусирует (собирает) или рассеивает. Но каковы свойства изображения, создаваемого линзой, и можно ли сделать его таким же, как у зеркала?
Основная функция линзы в зрительной системе заключается в фокусировке или рассеивании входящих лучей света симметрично вокруг оптической оси (см. рис. 1). В случае круглого театра или амфиктилоса зрительная ось — это линия, соединяющая центры сфер, определяющих линзу. Эта ось также является осью симметрии объектива.
Рисунок.
Зрительная ось определяет центр линзы. Графически линза показана на рисунке 2 ниже.
Рис. 2. Как определить центр выпуклой линзы.
Свет дважды изгибается при прохождении через линзу: один раз при входе в линзу и второй раз при выходе из нее.
Когда лучи света, идущие параллельно зрительной оси, проходят через собирающую линзу, они пересекаются в точке на зрительной оси. Эта точка называется фокусной точкой объектива и обозначается F. Расстояние этой точки от центра S линзы называется фокусным расстоянием F (см. рис. 3).
Рис. 3. Фокус F и фокусное расстояние F амбиентного объектива
ПРИМЕЧАНИЯ. Фокусная точка (F) фокусирующей линзы — это точка пересечения всех лучей света после их прохождения из линзы и параллельно зрительной оси перед входом в линзу.
Фокусное расстояние (f) объектива — это расстояние от фокуса (F) до центра линзы.
В случае большого мышления падающий пучок света отклоняется — лучи света, попадающие в линзу, мыслят о своем продолжении в одной точке. Это называется великим сосредоточением многих мыслей (см. рисунок 4). Он находится на той же стороне, что и источник линзы.
Рисунок 4. Средоточие многих мыслей
Как формируется изображение с помощью собирающей линзы?
Чтобы увидеть, какое изображение можно получить с помощью монтажного объектива, давайте проведем эксперимент.
Эксперимент 1: Наблюдайте за изображением, создаваемым линзой.
Что вам нужно?
- фонарик;
- кусок черного картона размером больше стекла фонарика;
- ножницы;
- скотч (липкая лента);
- большая лупа;
- белая картонная коробка (экран).
- Вырежьте стрелку в черной картонной коробке.
- С помощью скотча приклейте черный картон к экрану фонарика.
- Расположите лупу, фонарь и экран на оптической оси лупы.
- Измените положение фонаря и экрана для получения четкого изображения.
Какие выходы доступны?
Изменяя положение экрана и линзы по отношению к лупе, можно получить различные изображения: одно увеличенное, уменьшенное, перевернутое, прямое. Как вы знаете, централизованная линза не обязательно увеличивает наблюдаемый объект. Как это произошло?
Как и в случае с зеркалами, геометрические изображения с лучами света (см. рис. 5) помогают ответить на вопросы, поставленные в кратком изложении экспериментов, специально посвященных линзам.
Рисунок 5. Лучи света, используемые для построения изображения на коллекционной линзе
Если необходимо построить изображение с помощью собирающего объектива, обычно выбирают два из трех перечисленных ниже лучей.
- луч, параллельный оптической оси – после прохождения через линзу он проходит через фокус;
- луч, проходящий через центр линзы – после прохождения через линзу его направление (путь) не меняется;
- луч, проходящий через фокусную точку – после прохождения через линзу выходит параллельно оптической оси.
Последнее утверждение относится к тонкой линзе, использованной в эксперименте. Затем толщина линзы игнорируется и рисуется в виде линии, заканчивающейся стрелкой.
Изображение точки формируется разрезом как минимум двух лучей или их продолжением.
Положения объектов и положения изображений по отношению к признакам результирующего изображения обобщены в таблице 1 ниже.
| Положение объекта, x | Положение изображения, y | Особенности изображения |
| x > 2f | f < y < 2f | Перевернутое, действительное, уменьшенное |
| x = 2f | y = 2f | Перевернутое, действительное, имеет те же размеры, что и объект |
| 2f > x > f | y > 2f | Перевернутое, действительное, увеличенное |
| x = f | лучи проходят через линзу и параллельны друг другу | Без изображения |
| x < f | изображение появляется на той же стороне, что и объект | Прямое, мнимое, увеличенное |
Таблица 1. Характеристики изображения, создаваемого собирающей линзой
Из таблицы 1 можно сделать вывод, что особенности изображения, формируемого собирающей линзой, зависят от расстояния объекта от линзы.
Как создается изображение при использовании рассеивающей линзы?
Со многими идеями дело обстоит иначе. Лучи, падающие параллельно линзе, расходятся после выхода из линзы. Как и выше, расширение луча было преломлено, чтобы пересечь точку SO -Calcaled Fantastic Pocal Point (см. Рисунок 6).
Рисунок 6.Лучи, используемые для построения изображений с помощью пространственных линз.
Рассеивающие объективы (и съемочные объективы) требуют только два луча света для создания изображения.
- падающий луч, параллельный оптической оси – после прохождения через линзу падающий луч движется таким образом, что его продолжение проходит через мнимую фокусную точку;
- луч, проходящий через центр линзы – при прохождении через линзу он не меняет направления.
Помните! Многое продумано до мелочей, и в результате изображение всегда получается прямым, уменьшенным и великолепным.
Линза определяется как прозрачный, однородный материал с плоской поверхностью, сферической поверхностью и двумя преломляющими полированными поверхностями.
Собирающая линза
Если толщина линзы в центре больше, чем по краям, то лучи света, проходящие через линзу, искривляются по зрительной оси. В результате после профилактики такой линзой пучки света, параллельные зрительной оси, концентрируются в точке за линзой в зрительной оси фокальной плоскости.
Если луч падает на линзу, не параллельную оптической оси, он также сходится в точке, но эта точка находится в другой точке фокальной плоскости.
В любом случае луч, падающий на линзу, толщина которой в центре больше, чем по краям, будет сходиться в одной точке. Поэтому такая линза называется собирающей.
Рис. 2: Путь лучей в сходящейся линзе
Изображение, даваемое собирающей линзой
Чтобы построить изображение точки, заданной линзой, постройте путь лучей в линзе и проследите путь двух произвольных лучей, исходящих из точки. Если лучи пересекаются после прохождения через линзу, то в месте пересечения появляется изображение.
Поскольку лучи, проходящие через сходящуюся линзу, преломляются в направлении главной оптической оси, два луча, выходящие из одной точки, после прохождения через линзу пересекаются и образуют истинное изображение.
Следующие два луча обычно используются для построения изображения точки, полученного с помощью сходящейся линзы:
- луч, проходящий сквозь оптический центр линзы: он не будет преломляться, пройдёт сквозь линзу без изменений;
- луч, перпендикулярный линзе: после прохождения через линзу он будет направлен точно в фокус линзы.
Построив эти два луча, можно найти точку пересечения. Эта точка будет расположена за собирающей линзой и даст истинное изображение. Расстояние до изображения определяется типом тонкой линзы:
Точки O1 и О2 — центры сферических поверхностей, O1o2 — первичная оптическая ось, O — оптический центр, F — первичный фокус, F’ — вторичный фокус, OF’ — вторичная оптическая ось, F — фокальная плоскость.
Изображения, даваемые линзой
Посмотрев этот видеоурок, мы вспомним, что такое линза и для чего она используется. Мы рассмотрим основные характеристики тонких линз. Мы узнаем, как строятся изображения в тонкой линзе. Мы научимся определять характеристики изображений, полученных с помощью тонких линз. Мы также получим формулу для тонкой линзы.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
キットの他のビデオコースにアクセスするには、リストを購入して個人アカウントに追加する必要があります。
Конспект урока «Изображения, даваемые линзой»
В предыдущем уроке мы говорили о том, что линза — это прозрачное тело, ограниченное кривыми (чаще всего сферическими) или кривыми и плоскими поверхностями. Он используется для управления световыми лучами, то есть для изменения направления лучей.
Пока что мы с вами не знаем, как создать изображение предмета в тонкой линзе? На этот вопрос и ответит наш курс.
Сначала рассмотрим, как изобразить точечный источник света в монтажно-рассеивающей линзе. Для этого мы в основном будем использовать три «удобных луча» — лучи, путь которых после прохождения через линзу известен заранее:
1) лучи, идущие параллельно главной оптической оси, поскольку после дифракции в линзе они проходят через ее главный фокус (или проходят через ее расширения).
2) Из закона обратимости световых лучей следует, что лучи, проходящие через линзу через ее фокус, после преломления будут двигаться параллельно главной оптической оси — это второй набор лучей.
3) третий набор лучей выбирается в предположении, что лучи, проходящие через оптический центр линзы, не меняют направления.
Точка пересечения преломленных лучей на собирающей линзе или их проекций на рассеивающую линзу дает нам положение изображения точечного источника света.
Давайте усложним проблему. Предположим, что точечный источник света расположен на главной оптической оси линзы. Давайте найдем, где формируется образ:
Изображение в собирающей линзе реальное, так как формируется на пересечении самих преломленных лучей, а в рассеивающей линзе — мнимое, так как формируется на пересечении продолжений преломленных лучей.
Теперь рассмотрим, как формируются изображения протяженных объектов на разных расстояниях от собирающей линзы.
Во-первых, рассмотрите объект съемки за объективом с двойным фокусом.
Охарактеризуем полученное изображение. Во-первых, она реальна, так как получается при пересечении преломленных лучей. Во-вторых, она перевернута. И в-третьих, она уменьшена, о чем свидетельствует структура.
Обратите внимание, что если объект перпендикулярен главной зрительной оси, его изображение также будет перпендикулярно ей. Зная это, вы можете создать изображение точки B и отбросить его перпендикулярно главной оптической оси. Это делается следующим образом.
Аналогичным образом можно создавать и характеризовать изображения объектов, находящихся на других расстояниях от объектива.
Объект находится во втором фокусе объектива.
Объект находится между первым и вторым фокусами линзы.
Например, на киноэкране изображение такого типа. Он увеличен — экран намного больше, чем пленка, на которой был записан фильм. Изображения на экране действительно светятся. Чтобы пленка не оказалась перевернутой, потому что изображение на ней перевернуто, проектор также оснащен системой линз, каждая из которых помогает изменить направление световых лучей.