Как найти собственную скорость лодки
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.

Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. — 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. — Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
441-Х2=0
Х2=441
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Источники:
- решение задач на течение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание материала
- Скорость тела. Средняя скорость тела
- Видео
- Задача с рыбаком и лодкой
- Ширина русла и водоносность
- Задача с моторной лодкой
- Формулы, которые необходимо запомнить
- Движение по реке. Скорость течения реки
Скорость тела. Средняя скорость тела
Решение задач на движение опирается на хорошо известную из курса физики формулу
позволяющую найти путь S , пройденный за время t телом, движущимся с постоянной скоростью v .
Сразу же сделаем важное
Замечание 1. Единицы измерения величин S , t и v должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.
В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости, которая вычисляется по формуле
 |
(1) |
Например, если тело в течение времени t1 двигалось со скоростью v1 , в течение времени t2 двигалось со скоростью v2 , в течение времени t3 двигалось со скоростью v3 , то средняя скорость
 |
(2) |
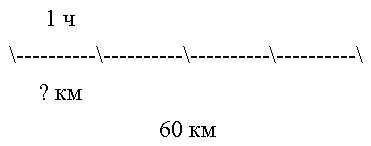
Задача 1. По расписанию междугородный автобус должен проходить путь в 100 километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на 25 минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на 20 км/час. Какова скорость автобуса по расписанию?
Решение. Обозначим буквой v скорость автобуса по расписанию и будем считать, что скорость v измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.
Рис. 1
Тогда


v + 20 – скорость автобуса во второй половине пути (в км/час);

В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:
Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:
Решим это уравнение:
По смыслу задачи первый корень должен быть отброшен.
Ответ. 40 км/час.
Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение. Воспользовавшись формулой (2), получаем
Ответ. 90 км/час.
Задача 3. Первую половину пути поезд шел со скоростью 40 км/час, а вторую половину пути – со скоростью 60 км/час. Найдите среднюю скорость поезда на протяжении всего пути.
Решение. Обозначим буквой S длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.
Рис. 2
Тогда


Следовательно, время, за которое поезд прошел весь путь, равно
В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути
Ответ. 48 км/час.
Замечание 2. Средняя скорость поезда в задаче 3 равна 48 км/час, а не 50 км/час, как иногда ошибочно полагают, вычисляя среднее арифметическое чисел (скоростей) 40 км/час и 60 км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по формуле (1).
Видео
Задача с рыбаком и лодкой
Разобравшись, как найти скорость течения реки, решим следующую задачу. Известно, что рыбак на лодке должен проплыть по реке 10 км. Проведя необходимые измерения, он установил, что течение в реке составляет 1 м/с. Какое время рыбаку понадобиться для того, чтобы по течению проплыть указанное расстояние, не используя при этом дополнительные средства тяги (мотор, весла).
Переводим скорость из м/с в км/ч, получаем 3,6 км/ч. Тогда искомое время будет равно:
t = S/v = 10/3,6 ≈ 2,8 ч.
Ширина русла и водоносность
Для более глубокого понимания вопроса, как найти скорость течения реки, важно знать еще один момент. Дело в том, что одна и та же река в разных местах может течь с различной скоростью. Причиной является изменение площади сечения ее русла, которое внешне связано с изменение ширины. Справедливости ради отметим, что не только изменение ширины, но и колебания в глубине влияют на быстроту течения воды (чем глубже, тем медленнее).
В виду сказанного выше, о скорости перемещения воды в реке имеет смысл говорить, если на достаточно длительном участке (километры и более) параметры ее русла колеблется незначительно, и река не имеет на этом участке притоков.
Более надежной характеристикой для любой реки является ее водоносность. Под водоносностью понимают объем воды, проходящий через вертикальное сечение русла за единицу времени. Водоносность не зависит от параметров русла, однако, она так же, как и скорость, изменится, если на рассматриваемом участке реки имеется приток.
В данной статье мы ограничимся предоставленной информацией о водоносности и перейдем к вопросу, как найти скорость течения реки.
Задача с моторной лодкой
Моторная лодка совершает каждый день переходы по реке из пункта A в пункт B. Дистанция между A и B составляет 7 км. Известно, что скорость лодки по течению равна 8 км/ч. Чему равна скорость течения, если на путь вниз по реке лодка затрачивает на 10 минут больше времени, чем при движении вверх по ней.
В данном случае мы не знаем ни скорость моторной лодки, ни скорость воды в реке. Обозначим первую как y, а вторую как x. Тогда можно записать следующие четыре уравнения:
x + y = 8;
S/t1 = x + y;
S/t2 = y — x;
t2 — t1 = 1/6
Первое уравнение отражает скорость лодки по течению, второе и третье уравнения связывают время и скорость при движении вниз и вверх по реке соответственно. Четвертое уравнение следует из условия задачи о разности времен прямого и обратного пути между пунктами A и B.
Сначала найдем из этих уравнений время t1 и t2:
t1 = 7/8 = 0,875 ч;
t2 = 1/6 + 7/8 = 1,0417 ч
Для определения скорости x воды в реке вычтем из второго третье уравнение, получим:
S/t1 — S/t2 = 2*x =>
x = S/2*(1/t1 — 1/t2)
Подставляем в это равенство рассчитанные величины t1 и t2, а также расстояние между пунктами S, получаем, что вода в реке течет со скоростью 0,64 км/ч.
Формулы, которые необходимо запомнить
Помимо приведенной выше информации, для решения задач на скорость течения реки следует запомнить несколько формул. Перечислим их.
Скорость течения является величиной постоянной, а вот скорость тела (лодки, катера, пловца) в общем случае может меняться, как по величине, так и по направлению. Для равномерного прямолинейного движения справедливой будет формула:
S = v*t
Где S — пройденный путь, v — скорость перемещения тела. Если движение происходит с ускорением a, тогда следует применять формулу:
S = a*t2/2
Помимо этих формул, для успешного решения задач следует уметь пользоваться тригонометрическими функциями при разложении векторов скорости на составляющие.
Теперь перейдем к решению конкретных задач.
Движение по реке. Скорость течения реки
В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.
По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.
Задача 4. Моторная лодка прошла по течению реки 14 км, а затем 9 км против течения, затратив на весь путь 5 часов. Скорость лодки в стоячей воде 5 км/час. Найдите скорость течения реки.
Решение. Обозначим буквой v скорость течения реки и будем считать, что скорость v измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.
Рис. 3
Тогда
5 + v – скорость, с которой лодка шла по течению реки (в км/час);

5 – v – скорость, с которой лодка шла против течения реки (в км/час);

Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:
Решим это уравнение:
По смыслу задачи первый корень должен быть отброшен.
Ответ. 2 км/час.
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.
Решение. Обозначим vс (км/ч) скорость лодки в стоячей воде и обозначим vр (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.
Рис. 4
Рис. 5
Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:
 |
(3) |
Если ввести обозначение
то, воспользовавшись формулой
vс = xvр ,
перепишем уравнение (3) в виде
 |
(4) |
Умножая уравнение (4) на vр , получим
По смыслу задачи первый корень должен быть отброшен.
Ответ. 7,5 .
Теги
Через уравнение.
S — пройденный путь, растояние, которое прошла, например, лодка. (км)
t — время, за которое она прошла расстояние S. (часов, минут)
V — собственная её скорость (км/ч, м/ч)
Такие задачи решаются далее: если известны: (под формулы подставляем числа)
t и V, то перемножаем — t * V, получаем S.
t и S, то расстояние делим время — S : t, получаем V
S и V, также — S : V, получаем t
Также если в задаче указана V (её ищем)
по течению, то V собственная + V по течению
против течения, то V собств. — V прот. теч.
Тогда формулы звучат так: если известны:
t и V, то t * (V с. +/- V) = S
t и S, то S : t = V с. +/- V
V и S, то S : (V c. +/- V) = t
Теперь ещё раз:
V c. — собственная скорость
V c. + V — скорость + скорость по теч.
V c. — V — скорость + скорость прот. теч.
Ну так чтоли… Плохой из меня учитель(((
Данный материал представляет собой систему
задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй — в ручей. Что же
произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в
ручейке — поплывет, так как вода в нем «бежит»
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке –
плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.
Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.
Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке,
собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути
разделить на время.
Чтобы найти время, необходимо длину пути
разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.
Такое движение называют движением по течению.
А в обратную сторону – движением против
течения.
Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4
часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
«помогает» плыть, а в другую — «мешает».
Рис.1
Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.
Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите собственную скорость
лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
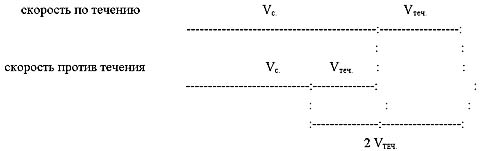
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
Vс. — собственная скорость,
Vтеч. — скорость течения,
V по теч. — скорость по течению,
V пр.теч. — скорость против течения.
Тогда можно записать следующие формулы:
V no теч = Vc + Vтеч ;
V np. теч = Vc — V теч.;
Попытаемся изобразить это графически:
Рис. 2
Вывод: разность скоростей по течению
и против течения равна удвоенной скорости
течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч — Vnp. теч ): 2
Задача.
1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните
таблицу:
|
V С. |
Vтеч. |
Vпо теч. |
Vпр.теч. |
|
|
1 |
12 км/ч |
3 км/ч |
||
|
2 |
23 км/ч |
25 км/ч |
||
|
3 |
24 км/ч |
20 км/ч |
||
|
4 |
4 км/ч |
17 км/ч: |
||
|
5 |
5 км/ч |
18 км/ч |
||
|
6 |
42 км/ч |
34 км/ч |
* — при решении п.6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.