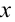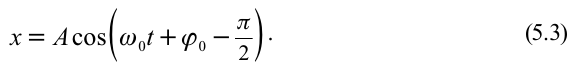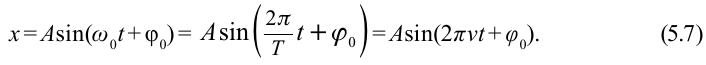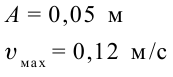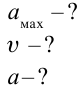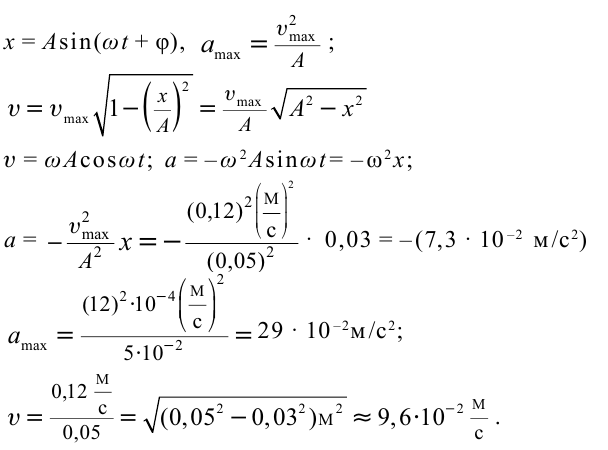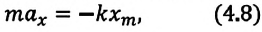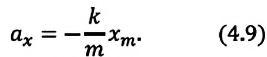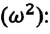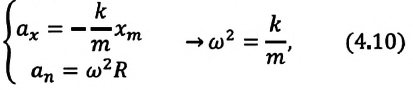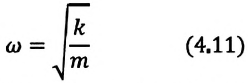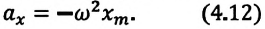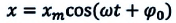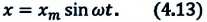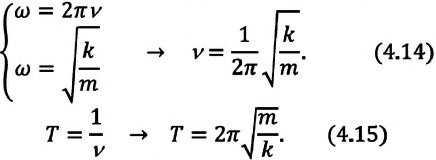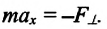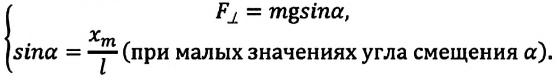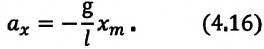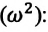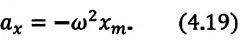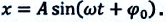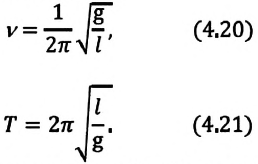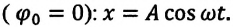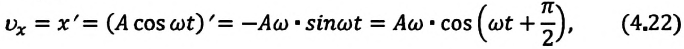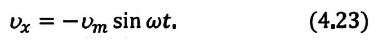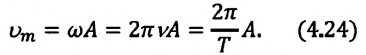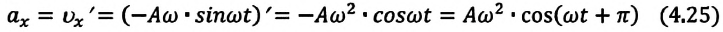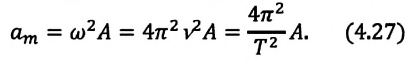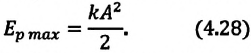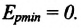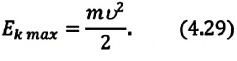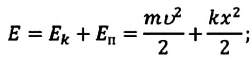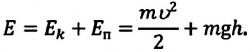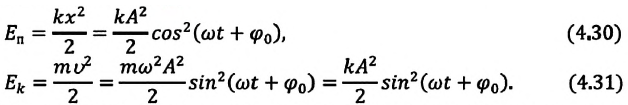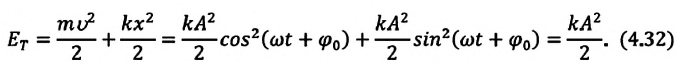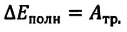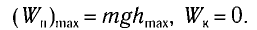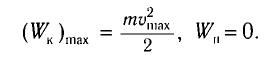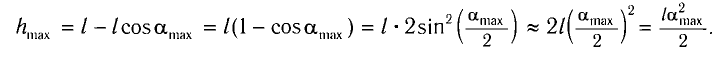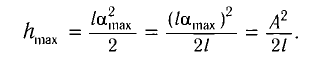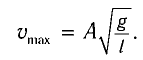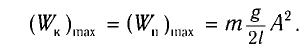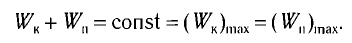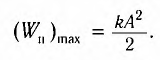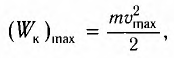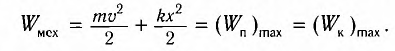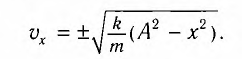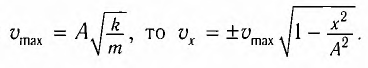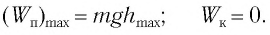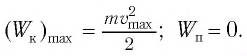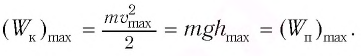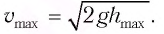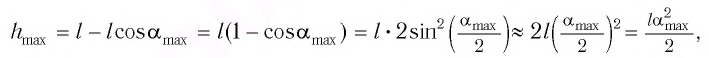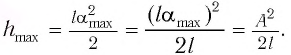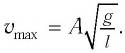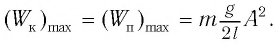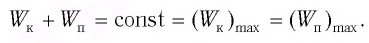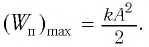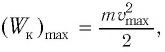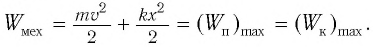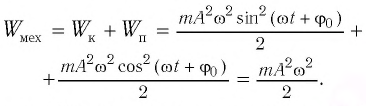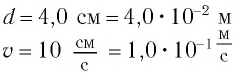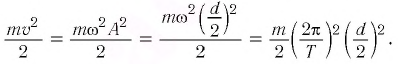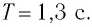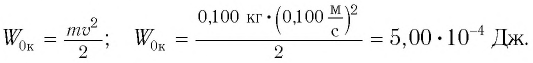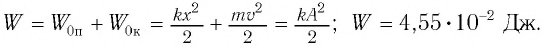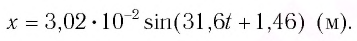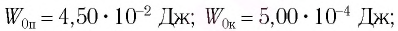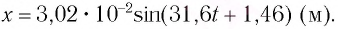Существуют различные
методы описания гармонических колебаний.
Приведём некоторые из них.
-
Аналитический
метод
Задаётся уравнение
колебаний гармонического осциллятора
х=Аsin(ωt+φ0)
по которому и
определяется смещение его от положения
равновесия в любой момент времени.
-
Графический
метод

график гармонического колебания
(рис.6.4) х=Аsin(ωt+φ0).
По оси абсцисс (ОХ) откладывается время
t
или фаза колебаний ωt+φ0,
по оси ординат (ОУ) – смещение х от
положения равновесия.
3. Метод векторной
диаграммы
Э
метод состоит в следующем. Гармоническое
колебание может быть задано с помощью
вектора, длина которого равна амплитуде
А колебания, а направление образует с
осью х угол, равный начальной фазе
колебания (рис. 6.5). Если привести этот
вектор во вращение с угловой скоростью
ω0,
то проекция конца вектора на ось х будет
перемещаться в пределах от +А до -А, а
колеблющаяся величина будет изменяться
со временем по закону
x
= Asin(ω0t+φ0),
совершая гармоническое колебание.
§ 6.1.6 Скорость и ускорение колеблющейся точки
Чтобы
найти скорость материальной точки при
гармоническом колебании, возьмем
производную от смещения колеблющейся
точки x
= Asin(ω0t+φ0)
по времени:
(6.18)
где
υmax
= Аω0
— максимальная скорость (амплитуда
скорости).
На
основании тригонометрических формул
преобразуем (4.18):
(6.19)
Сравнивая
выражения для смещения и скорости
замечаем, что фаза скорости
на больше фазы смещения, т.е. скорость
опережает по фазе смещение на
Продифференцировав (4.18), найдем
ускорение:
(6.20)
где
аmax
= А ω02
— максимальное ускорение (амплитуда
ускорения).
Вместо
(6.20) запишем
а
= аmax
соs
[π + (ω0t+φ0)] (6.21)
Из
сравнения (6.21) и (6.17) следует, что фазы
ускорения и смещения различаются на π,
т. е. эти величины изменяются в противофазе.
Это значит, что при положительном
максимальном смещении ускорение
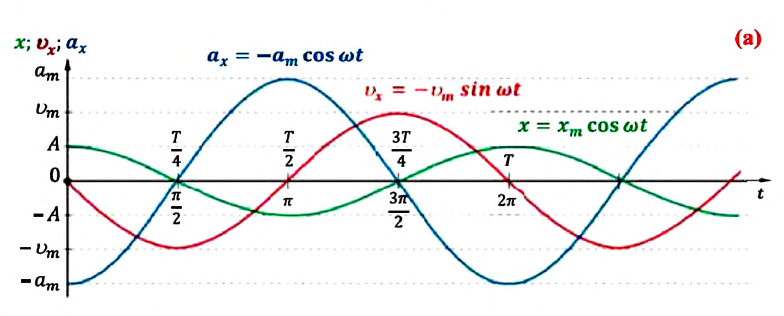
максимально, но отрицательно. На рисунке
показаны графические зависимости
смещения, скорости и ускорения от времени
(рис.6.6, а) и их векторные диаграммы
(рис.6.6, б) .
§ 6.1.7 Кинетическая и потенциальная энергии колебательного движения
Гармонический
осциллятор обладает как кинетической,
так и потенциальной энергией, которые
последовательно переходят друг в друга
при колебаниях осциллятора. Полная
энергия осциллятора равна сумме
кинетической и потенциальной энергии:
Е
= Ек+Еп
(6.22)
Кинетическая
энергия осциллятора, колеблющегося по
гармоническому закону, вычисляют по
формуле:
(6.23)
с
учётом mω2
=
k
Потенциальную
энергию колебательного движения найдём,
исходя из формулы для потенциальной
энергии упругой деформации:
(6.24)
Складывая
кинетическую и потенциальную энергию,
получим полную механическую энергию
материальной точки, колеблющейся по
гармоническому закону:

Полученное
выражение показывает, что энергия
гармонического осциллятора от времени
не зависит, т.е. с течением времени
остаётся величиной постоянной, а зависит
только от квадрата амплитуды и частоты.
При
отсутствии сил трения полная механическая
энергия системы не изменяется:
(6.26)
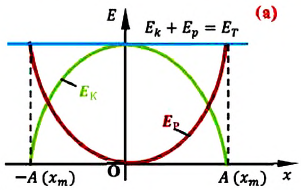
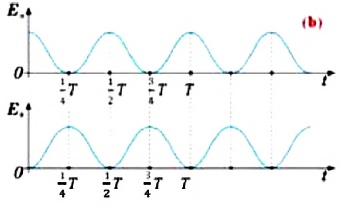
Графически
зависимости кинетической, потенциальной
и полной механической энергий колеблющейся
системы от времени показаны на рис. 4.7,
а.
Потенциальная
яма (ограниченная область пространства,
в которой потенциальная энергия меньше,
чем в не её), соответствующая гармоническому
колебанию, изображена на рис. 6.7, б. Она
определяется зависимостью
.
Отложив на оси ординат полную механическую
энергию Е, по графику определяют интервал
координат (-А, +А), за пределы которого
частица, обладающая такой энергией,
выйти не может.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 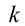
Если груз, который находится в равновесии, потянем вправо на расстояние 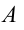
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
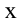
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 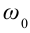
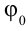
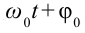
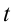
Из математики известно, что 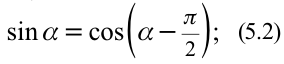
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 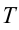

б) частота колебания 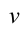
Единица
c) циклическая частота 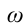
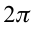
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
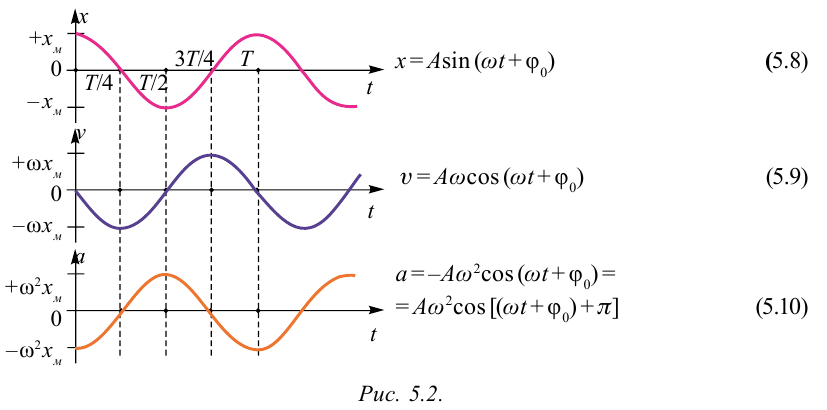
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
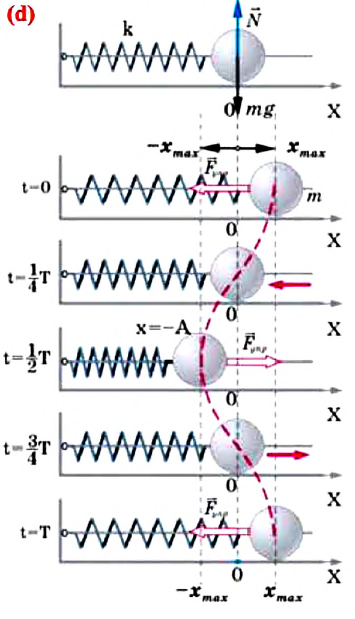
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 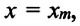
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 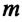
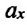
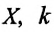
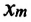
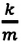
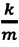
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 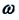
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 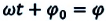
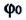
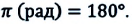
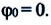

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
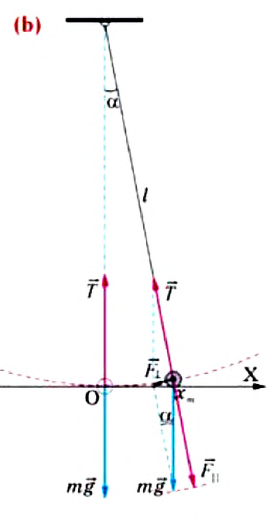
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 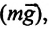
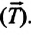
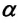
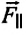
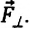
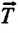
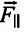
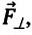
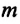
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 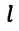
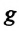
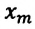
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 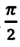
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 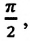
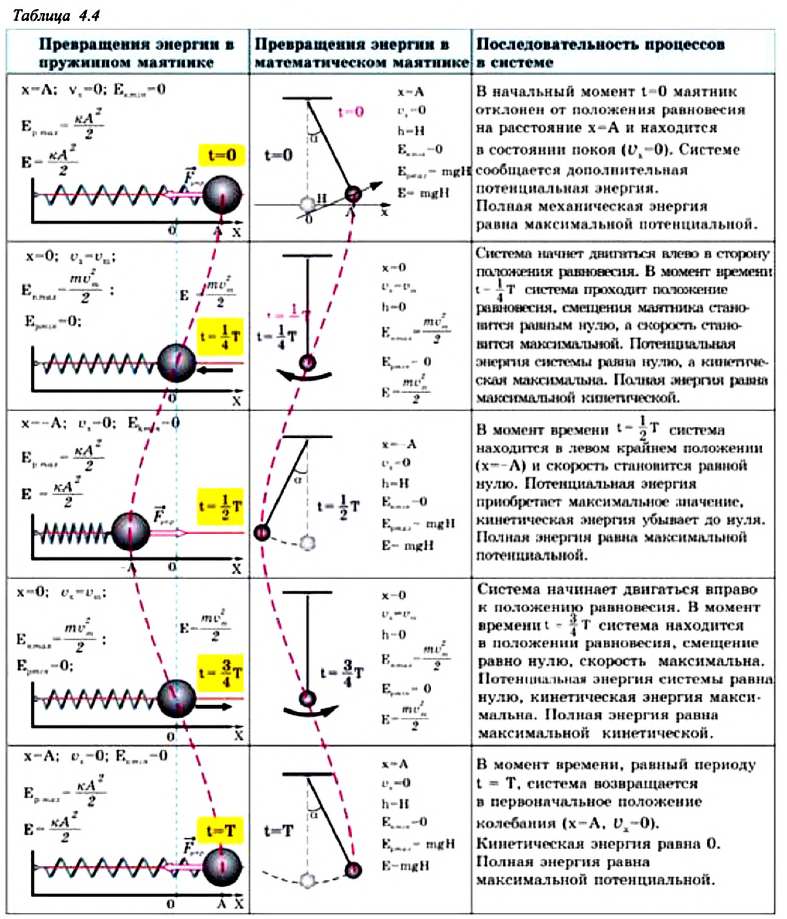
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 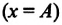
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 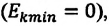
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 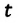
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
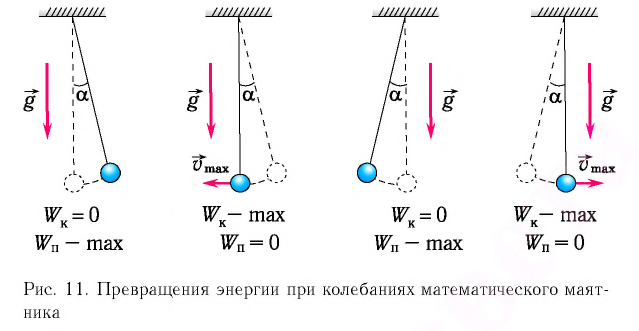
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
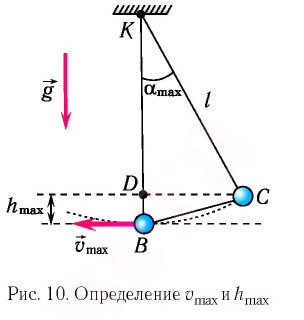
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
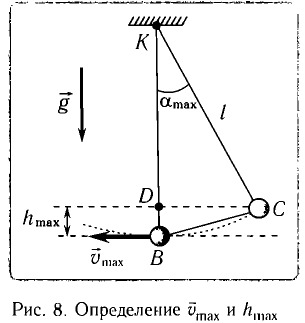
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
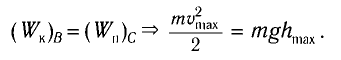
Отсюда найдем модуль максимальной скорости маятника:
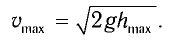
Высоту 
Если колебания малые, то 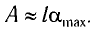
Отсюда
Подставив выражение для 
Подставляя выражения для 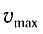

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 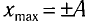
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
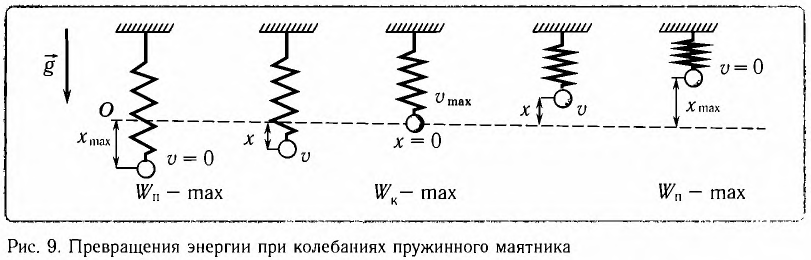
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 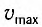
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 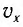
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 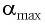
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 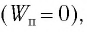
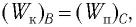
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 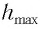
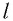
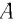
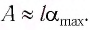
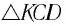
или
Подставив выражение (3) для 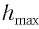
Подставляя выражения (3) для 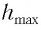
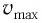
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
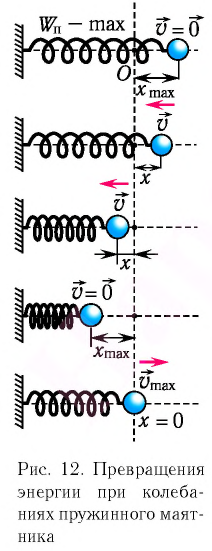
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 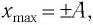
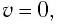
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 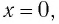
где 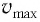
В положениях между крайними точками полная энергия
С учетом выражений для координаты 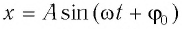
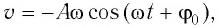
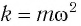
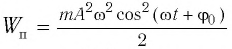
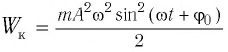
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 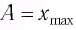
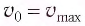
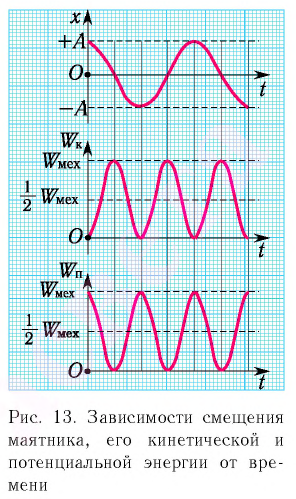
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 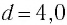
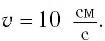
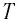
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 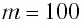
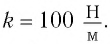
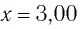
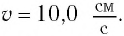
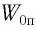
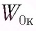
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 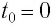
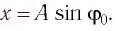
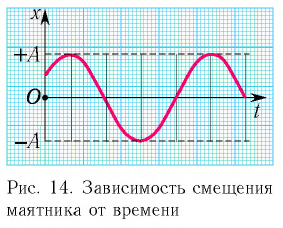
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
Содержание книги
Предыдующая страница
§17. Механические колебания
17.4 Качественный анализ движения материальной точки.
Во многих случаях характер поведения механической системы может быть проанализирован без точного решения уравнений движения. В данном разделе мы рассмотрим один из методов такого качественного анализа.
Пусть материальная точка массы m может двигать вдоль прямой, с которой мы совместим ось Ox декартовой системы координат. Для расчета закона движения этой точки используется уравнение второго закона Ньютона
(~ma = F) , (1)
где a — ускорение точки, F — сумма всех сил, действующих на материальную точку (точнее сумма проекций сил на выбранную ось). В общем случае силы, действующие на тело, могут быть постоянными, а также зависеть от времени, координаты точки, от ее скорости. Поэтому с математической точки зрения уравнение (1) следует рассматривать как уравнение относительно неизвестной функции x(t) — закона движения. Помимо самой неизвестной функции в это уравнение входят ее производные[1]: первая производная x′ = υ(t) — мгновенная скорость точки, вторая производная x′′ = a — ее ускорение. При задании начальных условий (начальной координаты и начальной скорости) это уравнение имеет единственное решение, которое и определяет точный закон движения материальной точки. Однако, в большинстве случаев точное решение уравнения (1) вызывает значительные математические трудности, поэтому очень часто его решают численно с помощью компьютера. Один из простейших методов такого численного решения был рассмотрен нами при изучении кинематики.
Если сумма всех сил, действующих на тело, равна нулю, движение такого тела является равномерным. Если все силы, действующие на тело, постоянны (как по величине, так и по направлению), то и их сумма также постоянна. В этом случае движение тела является равноускоренным и его описание не вызывает никаких сложностей.
17.4.1 Автономные системы.
Многие из уже изученных нами сил зависят от положения тела (его координаты). Такими силами являются силы всемирного тяготения, силы электростатического взаимодействия, силы упругости. Если на тело действую только такие силы, то уравнение движения (1) приобретает вид
(~ma = F(x)) . (2)
Такая физическая система, уравнения движения корой не содержат в явном виде ни времени, ни скорости частиц, называется автономной. Поведение таких систем можно качественно проанализировать на основании закона сохранения механической энергии. Преобразуем уравнение (1) следующим образом. Запишем выражение для ускорения[2] как «скорость изменения скорости» (~a = frac{Delta upsilon}{Delta t}) и умножим уравнение на Δx — малое изменение координаты тела
(~mfrac{Delta upsilon}{Delta t} Delta x = F(x) Delta x) . (3)
В этом уравнении величина (~mfrac{Delta upsilon}{Delta t} Delta x = m Delta upsilon frac{Delta x}{Delta t} = m upsilon Delta upsilon = Delta left( frac{m upsilon^2}{2} right)) есть изменение кинетической энергии тела на малом интервале изменения его координаты. Величина (F(x) Delta x = delta A) является работой, совершенной над телом на этом же интервале изменения координаты. Так как силы, действующие на рассматриваемое тело, зависят только от координаты, то работа этих сил может быть представлена как уменьшение потенциальной энергии тела (delta A = −Delta U) . Понятно, что потенциальная энергия является некоторой функцией от координаты тела U(x). Таким образом, проведенные математические преобразования приводят нас к уравнению закона сохранения механической энергии: увеличение кинетической энергии тела равно убыли его потенциальной энергии; или сумма кинетической и потенциальных энергий тела остается постоянной
(~frac{m upsilon^2}{2} + U(x) = operatorname{const}) . (4)
Константа в этом уравнении имеет смысл полной механической энергии движущегося тела E и может быть определена из начальных условий.
Связь между потенциальной энергией и действующей силой следует из сравнения выражений для работы произведенной над телом (F(x) Delta x = — Delta U) , откуда находим, что сила равна производной от потенциальной энергии по координате, взятой с противоположным знаком
(~F(x) = -frac{Delta U}{Delta x} = -U'(x)) . (5)
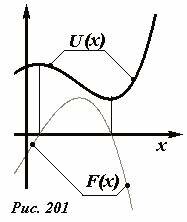
Связь между этими двумя функция может быть проиллюстрирована и графически (Рис. 201): если функция U(x) возрастает, то F(x) отрицательна; если U(x) убывает, то F(x) положительна; в точках экстремумов функции U(x) функция F(x) обращается в нуль. Следует также запомнить, что действующая сила всегда направлена в сторону убывания потенциальной энергии. Отметим также, что выражение (5) определяет потенциальную энергию с точностью до постоянного слагаемого – с этим, парадоксальным на первый взгляд, обстоятельством мы уже неоднократно встречались.
Подобный вывод мы уже проводили, при рассмотрении закона сохранения энергии. Здесь же подчеркнем, что сделанные нами преобразования носят математический характер, поэтому, если удалось получить уравнение движения вида (2), то всегда можно перейти к эквивалентному уравнению (4), в котором функция U(x) удовлетворяет соотношению (5) – не зависимо от того, является ли функция F(x) силой, а U(x) — потенциальной энергией. Напомним, для того, чтобы ввести понятие потенциальной энергии для того или иного вида взаимодействия, необходимо доказать, что это взаимодействие является потенциальным, то есть что работа не зависит от вида траектории, а определяется только начальным и конечным положением. Такие силы называются консервативными, и системы, в которых действую только такие силы, также называются консервативными. В некоторых случаях удается провести преобразование от уравнения (2) к уравнению (4) даже если нельзя говорить строго о потенциальной энергии, в такой ситуации функцию U(x) называют эффективной потенциальной энергией.
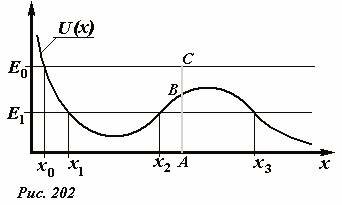
Дадим теперь наглядную геометрическую иллюстрацию уравнения (4). Для этого построим график зависимости потенциальной энергии тела от его координаты U(x) (На Рис. 201 приведен пример возможной зависимости). График зависимости потенциальной энергии от координаты называют потенциальной кривой. На этом же графике проведем горизонтальную прямую, соответствующую уровню полной механической энергии точки. Пусть, например, эта энергия равна E0 . В точке с произвольной координатой A длина вертикального отрезка AB равна потенциальной энергии тела, длина отрезка AC — есть полная энергия тела, следовательно, длина отрезка BC выражает кинетическую энергию рассматриваемого тела. Так как кинетическая энергия не может быть отрицательной, то тело не может находиться в тех точках оси, где потенциальная энергия больше его полной энергии. Таким образом, горизонтальная прямая, проведенная на уровне полной энергии отсекает на потенциальной кривой допустимые области движения тела: только те, где потенциальная кривая лежит ниже прямой полной энергии. Так для уровня энергии E0 (на Рис. 202) запрещенной является область x < x0 , то есть движение точки возможно только при x0 ≥ x. В точках пересечения уровня полной энергии с потенциальной кривой полная энергия равна потенциальной, следовательно, кинетическая энергия и скорость тела в этой точке обращается в нуль. Такие точки называются точками возврата.
Если полная энергия тела, в рассматриваемом примере уменьшится до значения E1, то для него возникнет еще одна запрещенная область движения x2 < x < x3. В этом случае движение тела возможно либо в ограниченной области x1 ≤ x ≤ x2 (понятно, что в этом случае тело будет совершать колебания между указанными точками), либо в неограниченной с одной стороны области x ≥ x3.
Таким образом, потенциальная кривая и уровень полной энергии определяют области движения тела.
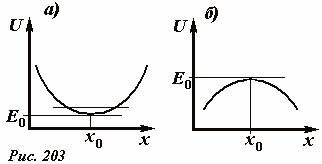
Весьма интересным случаем является совпадение уровня полной энергии E0 с минимумом потенциальной энергии (Рис. 203 а).
Область, в которой потенциальная кривая содержит точку минимума, часто называют потенциальной ямой. В этой ситуации разрешенная область движения сужается до единственной точки x0, которая является точкой равновесия: в этой точке сумма сил, действующих на тело равна нулю. Если же незначительно увеличить энергию тела, то оно начнет колебаться вокруг этой точки: при незначительном отклонении от положения равновесия возникают силы направленные к положению равновесия, стремящиеся вернуть тело в это положение. Такое положение равновесия называется устойчивым. Минимум потенциальной кривой указывает на точку устойчивого равновесия тела. Если полная энергия тела совпадает с максимумом потенциальной энергии (Рис. 203 б), в точке максимума тело также находится в состоянии равновесия, так как здесь сумма сил также равна нулю. Однако, при малом отклонении от этого положения скорость тела начинает возрастать – тело все дальше удаляется от положения равновесия. Такое положения равновесия является неустойчивым: при малом отклонении от него возникаю силы, стремящиеся еще дальше увести тело от этого положения. Так как в реальности, каждое тело подвержено незначительным внешним воздействиям, то тело в положении неустойчивого равновесия находиться длительное время не может.

Проведенные рассуждения становятся очевидными, если воспользоваться следующей аналогией (Рис. 204). В поле тяжести потенциальная энергия тела пропорциональна высоте (U = mgh), поэтому профиль потенциальной кривой совпадает с профилем поверхности, на которой находится рассматриваемое тело. Поэтому поведение тела в некотором потенциальном поле, описываем функцией U(x) полностью аналогично поведению шарика (чтобы трение было пренебрежимо малым), катающемуся по горке с профилем, совпадающим с потенциальной кривой.
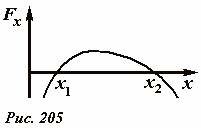
Анализ устойчивости положения тела можно провести и на основе рассмотрения зависимости результирующей силы от координаты. Для примера на Рис. 205 построен график зависимости проекции результирующей силы Fx, действующей на тело, от его координаты. Положениям равновесия соответствуют точки, в которых Fx = 0, на рисунке показаны две таких точки x1, x2. Что бы определить устойчивость необходимо мысленно сдвинуть тело на малое расстояние от положения равновесия. Так при смещении тела на небольшое расстояние δx в положительном направлении от точки x1 результирующая сила положительна, следовательно, тело продолжит движение в том же направлении. Аналогично, при смещении в отрицательном направлении возникнет отрицательная сила, которая еще дальше будет уводить тело от точки x1: следовательно, эта точка есть точка неустойчивого равновесия. Противоположна ситуация вблизи точки x2: при малом смещении тела от этой точки возникает сила противоположного знака, которая возвращает тело к точке x2, следовательно, это точка устойчивого равновесия.
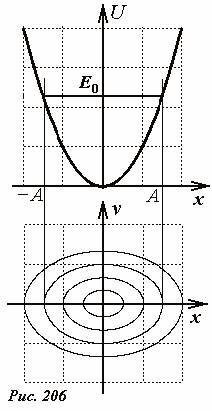
Наконец, еще одно общее рассуждение, касательно возможностей качественного анализа. Оказывается, потенциальные кривые прекрасно сочетаются с фазовыми траекториями — по заданной потенциальной кривой можно построить набор фазовых траекторий, соответствующих различным значениям полной энергии. Такой набор фазовых траекторий также называется фазовым портретом системы. Под графиком потенциальной кривой изобразим участок фазовой плоскости, так чтобы оси X были параллельны и начала их отсчета совпадали (рис.206).
Для примера рассмотрим потенциальную кривую, соответствующую гармоническим колебаниям. На графике потенциальной энергии зададим уровень полной энергии системы E0 горизонтальной прямой, точки пересечения которой с потенциальной кривой определяют крайние точки — проводя вертикальные прямые их можно отметить на фазовой плоскости. Величину скорости при произвольном значении координаты можно оценить из разности полной и потенциальной энергии. Если же пользоваться компьютером, то можно построить точно. Из уравнения (4) выразим зависимость скорости от координаты
(~upsilon = pm sqrt{frac{2}{m}(E_0 — U(x))}) .
Как следует из этого выражения фазовая траектория симметрична относительно оси x , что понятно с точки зрения здравого смысла: в процессе колебательного движения за один период тело проходит каждую точку дважды — один раз в одном направлении, другой в противоположном, причем модули скорости при прохождении одной точки одинаковы. Как и следовало ожидать, движение точки является колебательным (можно даже уточнить – колебания гармонические), так как фазовые траектории являются эллипсами.
17.4.2 Диссипативные системы.
Если на тело, движущиеся вдоль оси Ox, действуют силы, приводящие к уменьшению механической энергии системы, то такие силы (и такие системы) называются диссипативными[3]. Такие силы зависят от скорости, например, силы сопротивления воздуха, силы вязкого трения. Заметим, что даже сила сухого трения, подчиняющаяся закону Кулона-Амонтона, так же зависит от вектора скорости, так как эта сила всегда направлена в сторону противоположную вектору скорости.
С другой стороны, сила Лоренца, действующая на движущуюся заряженную частицу со стороны магнитного поля, также зависит от скорости, но не является диссипативной. Так как эта сила перпендикулярна вектору скорости, то она не совершает работы, следовательно, не изменяет энергии тела.
Качественно поведение таких систем также возможно проанализировать на основании рассмотрения потенциальной кривой. При наличии слабого затухания полная механическая энергия системы будет медленно уменьшаться, что соответствует медленному понижению уровня полной энергии.
Особенно наглядно можно провести такой анализ с помощью фазового портрета системы, построенного без учета потерь энергии.
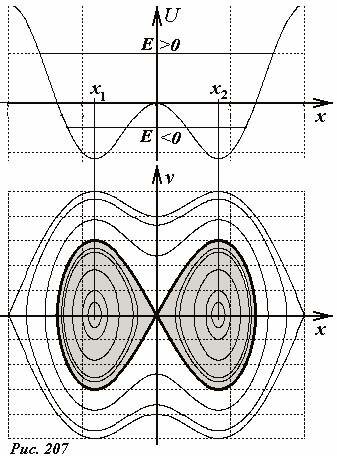
Пусть потенциальная кривая для некоторого тела имеет вид, показанный на рис. 207. Ниже построен фазовый портрет системы. Потенциальная кривая симметрична и содержит две точки минимума x1, x2 (две потенциальные ямы), соответствующие положениям устойчивого равновесия, разделенных точкой неустойчивого равновесия x = 0. В зависимости от величины полной энергии будет меняться и характер движения тела. Так при положительной энергии E > 0 тело движется симметрично относительно начала отсчета, огибая обе ямы. Когда тело проходит начало координат отсчета его скорость минимальна. Фазовые траектории в этом случае также симметричны и охватывают обе точки устойчивого равновесия x1, x2.
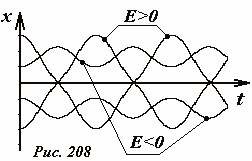
Если полная энергия тела отрицательна, то оно может двигаться только в одной из потенциальных ям – ему не хватает энергии, чтобы преодолеть потенциальный барьер, их разделяющий. В этом случае фазовые траектории также замкнуты, но охватывают только одну из точек устойчивого равновесия, какую именно — определяет начальное положение. Эта область на фазовом портрете на рисунке заштрихована. Графики зависимости координаты от времени для разных значений энергии и начальных положений точки показаны на рис. 208.
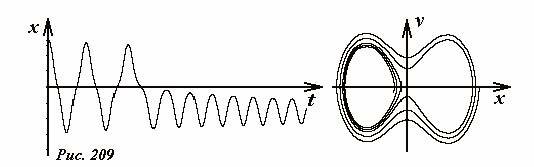
При наличии потерь малых потерь механической энергии фазовая траектория движения тела будет «сжиматься» переходя с одной фазовой траектории Рис. 207 на другую, соответствующую меньшей энергии. На рис. 209 показана одна из возможных фазовых траекторий, которая, в конце концов, придет к одному из положений устойчивого равновесия. Заметим, что предугадать в какую именно из двух потенциальных ям попадет тело практически невозможно: это зависит от начального положения тела, параметров сил трения, и даже если эти характеристики известны, может быть случайным.
17.4.3 Малые колебания в произвольных колебательных системах.
Проведенный анализ общих свойств колебательных систем показывает, что необходимым условием возможности колебательного движения в произвольной системе является наличие положения устойчивого равновесия. В этом случае при отклонении тела от положения равновесия возникнет возвращающая сила, направленная к положению равновесия. Под действием этой силы тело приобретет некоторую скорость, которая будет максимальна при достижении положения равновесия. Далее тело по инерции проскочит положение равновесия и отклонится от него в противоположную сторону. После чего процесс повторится. Таким образом, вторым условием возможности колебаний является наличие у системы инерционных свойств – тело нулевой массы свободно колебаться не может. При отсутствии сил трения процесс колебаний будет продолжаться бесконечно, если же силы трения значительны, то даже при наличии положения устойчивого равновесия колебания не возможны.
Рассмотрим теперь описание движения материальной точки вблизи положения устойчивого равновесия. Как и прежде будем основываться на уравнении второго закона Ньютона
(~ma = F_x(x)) , (1)
где Fx(x) — проекция результирующей силы на ось, вдоль которой движется тело.
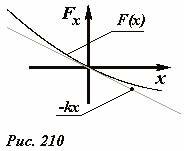
Совместим начало отсчета x = 0 с положением равновесия тела. В этой точке результирующая сила равна нулю Fx(0) = 0. Графически это выражается тем, что график зависимости Fx(x) пересекает ось Ox (Рис. 210) под некоторым отрицательным углом[4]. При малом отклонении от положения равновесия функцию Fx(x) можно приближенно заменить линейной[5]
(~F_x(x) approx — kx) . (2)
График этой приближенной функции является прямой линией. Очевидно, что наименьшая погрешность приближения будет достигнута в том случае, если построенная прямая будет являться касательной к графику функции Fx(x). Следовательно, коэффициент наклона построенной прямой должен совпадать с производной функции Fx(x) в точке равновесия x = 0
(~k = — F’_x(0)) . (3)
Таким образом, если произвольную силу вблизи положения равновесия заменить[6] линейным приближением (2) с коэффициентом пропорциональности (3), то уравнение движения преобразуется в уравнение гармонических колебаний
(~ma = — kx) , (4)
с частотой
(~omega = sqrt{frac{k}{m}} = sqrt{-frac{F’_x(0)}{m}}) . (5)
Аналогичный результат модно получить и с помощью энергетического подхода к описанию движения рассматриваемого тела. Так закон сохранения механической энергии выражается уравнением
(~frac{m upsilon^2}{2} + U(x) = E) , (6)
где E — сохраняющаяся полная механическая энергия тела, U(x) — его потенциальная энергия. Положению устойчивого равновесия соответствует точка минимума функции U(x).
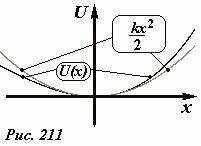
При малом отклонении от положения равновесия график этой функции можно приближенно описать параболой (Рис. 211)
(~U(x) approx frac{k x^2}{2}) . (7)
В этом выражении коэффициент пропорциональности k совпадает с коэффициентом в формуле (2). Для доказательства этого утверждения достаточно вспомнить формулу, связывающую потенциальную энергию с действующей силой: сила равно производной от потенциальной энергии, взятой с противоположным знаком (F_x = — U'(x)). Именно при записи приближенного выражения для потенциальной энергии в виде (7) из него непосредственно следует выражение (2):
(~F(x) = -left( frac{k x^2}{2} right)’ = — kx) .
Приближенная формула (7) для потенциальной энергии приводит к уравнению гармонических колебаний в форме
(~frac{m upsilon^2}{2} + frac{k x^2}{2} = E) . (8)
Подведем итог общего рассмотрения: вблизи положения устойчивого равновесия тело может совершать колебания, если возвращающая сила может быть представлена в виде (F_x(x) approx -kx), а потенциальная энергия в форме (U(x) approx frac{k x^2}{2}), то малые колебания являются гармоническими.
17.4.4 Математический маятник: не гармонические колебания.
Наиболее типичным и наглядным примером использования приближения малых колебаний является описание колебаний математического маятника. При больших углах отклонения использование приближения малых углов неприменимо, в этом случае необходимо искать решение точного уравнения движения
(~varepsilon = -frac{g}{l} sin varphi) , (1)
где ε — угловое ускорение маятника. К сожалению, это уравнение с математической точки зрения, очень сложно. Функции, являющиеся решениями этого уравнения при различных начальных условиях, не выражается через элементарные функции. Можно, конечно, решить это уравнение численно[7] с помощью компьютера. Мы не будем рассматривать эти методы, ограничимся указанием принципиальных отличий решений уравнений (1) от приближения малых углов. Важнейшим из них является не гармоничность колебаний. Конечно, решениями этого уравнения являются периодические функции, которые по теории Фурье можно представить в виде суммы (бесконечной) гармонических функций кратных частот. Иными словами, в колебаниях математического маятника появляются кратные частоты – обертона.
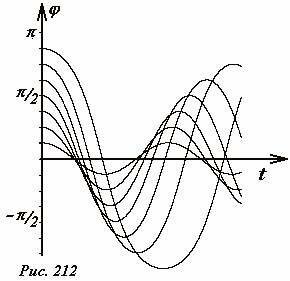
На Рис. 212 показаны графики зависимости угла отклонения маятника от времени при различных амплитудах колебаний, полученных с помощью численных расчетов. Конечно, определить на глаз являются ли полученными синусоидами, или нет невозможно.
Вторым важным отличием точного решения (1) от приближенного является зависимость периода колебаний от их амплитуды, что хорошо видно на Рис. 212. Покажем, как может быть рассчитана (опять же численно) эта зависимость. Пусть нить маятника отклонена на угол φ0. Разобьем диапазон изменения координаты [-φ0,φ0] точки на малые интервалы (~Delta varphi = frac{varphi_0}{N}), тем самым получим набор точек разбиения (varphi_k = k Delta varphi) , k = −N,−N + 1,… −1,0,+1,+2,…,+N.
Используя закон сохранения энергии для маятника
(~frac{m l^2 omega^2}{2} — mgl cos varphi = — mgl cos varphi_0) ,
мы можем вычислить скорости маятника ωk в момент прохождения точек φk
(~omega_k = sqrt{2 frac{g}{l} (cos varphi_k — cos varphi_0)}) .
На каждом интервале (Delta varphi_k = varphi_k — varphi_{k-1}) оценим среднюю скорость как среднее арифметическое значение скоростей на концах интервала (overline {omega_k} = frac{omega_k + omega_{k-1}}{2}). Тогда время Δtk, за которое маятник пройдет интервал (Delta varphi_k = varphi_k — varphi_{k-1}) можно найти по формуле (~Delta t_k = frac{Delta varphi_k}{overline {omega_k}} = frac{2 Delta varphi}{omega_k + omega_{k-1}}), после чего останется только просуммировать эти значения по всем интервалам разбиения — полученная сумма будет равна половине периода колебания. Такой метод также является приближенным, но уменьшение шага разбиения всегда будет приводить к увеличению точности расчетов. Замена средней скорости среднеарифметическим является точной при равноускоренном движении, поэтому это приближение соответствует приближению равноускоренного движения на малом интервале.
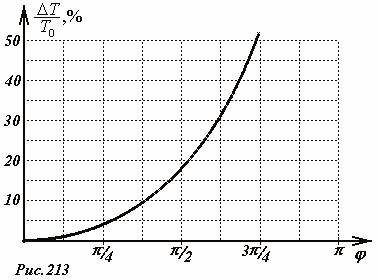
Не вдаваясь в технические детали расчета (при наличии времени и терпения его можно провести и на бумаге) приведем результаты расчета, полученные при разбиении диапазона изменения угла на двести равных интервалов. Результаты расчетов представлены на рис.213. Здесь, (~T_0 = 2pi sqrt{frac{l}{g}}) — период малых колебаний, (~frac{Delta T}{T_0} = frac{T — T_0}{T_0})- относительное изменение периода колебаний при увеличении их амплитуды.
Имея эту кривую, можно ответить на вопрос, какие же колебания можно считать «малыми»? Ответ зависит от той точности, которая для вас является достаточной. Так, при амплитуде колебаний (~varphi_0 = frac{pi}{4}) их период превышает период малых колебаний менее чем на 5%, а при амплитуде (~varphi_0 = frac{pi}{2}) период возрастает всего на 18%. Отметим, что полученная зависимость приближенно может быть описана формулой
(~T approx T_0 left(1 + frac{varphi^2_0}{16} right)) .
В заключение данного раздела укажем, что полученные результаты полностью подтверждаются экспериментальными данными.
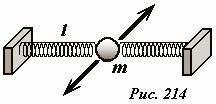
Рассмотрим еще один пример колебательной системы: небольшой шарик массы m расположен на гладкой горизонтальной поверхности и прикреплен с помощью двух пружин жесткости k длиной l к двум неподвижным упорам (Рис. 214). В положении равновесия все элементы системы находятся на одной прямой, при этом пружины не деформированы. Брусок совершает колебания в направлении перпендикулярном пружинам.
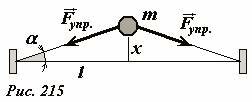
Положение шарика будем задавать его смещением x от положения равновесия. В процессе движения на шарик действуют силы упругости со стороны пружин (Рис. 215). Уравнение движения шарика имеет вид
(~ma = -2 F_{ynp} sin alpha) . (1)
Выразим силы упругости и синус угла отклонения через величину отклонения x, считая его малым. Для вычисления силы упругости воспользуемся законом Гука и приближенной формулой
(~F_{ynp} = k Delta l = k (sqrt{l^2 + x^2} — l) = kl left(sqrt{1 + frac{x^2}{l^2}} — l right) approx kl left( left( 1 + frac{1}{2} frac{x^2}{l^2}right) — l right) = frac{k x^2}{2 l}) .
Если считать отклонение малым, то и угол α также будет малым, поэтому
(~sin alpha approx operatorname{tg} alpha = frac{x}{l}) .
В этом приближении уравнение движения шарика будет иметь вид
(~ma = -frac{k}{2 l^2} x^3) . (2)
Таким образом, даже малые колебания шарика в рассматриваемой системе не являются гармоническими. Аналитического решения полученного уравнения (2) также не существует. Анализ этого уравнения показывает, что период колебаний шарика в этой системе сильно зависит от амплитуды (даже при малых амплитудах): он убывает обратно пропорционально амплитуде.
То, что период гармонических колебаний не зависит от амплитуды, является в некотором смысле «счастливым совпадением»: при возрастании амплитуды, с одной стороны», колебаний возрастает путь, проходимый телом, с другой – возрастает средняя скорость движения. Для гармонических колебаний эти два фактора полностью компенсируют друг друга! Для математического маятника – путь возрастает быстрее, чем средняя скорость, поэтому период его колебаний незначительно возрастает при возрастании амплитуды. В рассмотренном примере средняя скорость возрастает значительно быстрее, чем путь, проходимый шариком – в этом случае период колебаний быстро убывает при возрастании амплитуды.
Примечания
- ↑ Такие уравнения называются обыкновенными дифференциальными уравнениями.
- ↑ Для тех, кто уже познакомился с производными, можно было бы уже записывать эти математические преобразования на языке бесконечно малых величин. Но чтобы не пугать остальных мы сохраним пока прежние обозначения.
- ↑ от латинского dissipatio – рассеивание.
- ↑ Если угол наклона положителен (то есть функция возрастающая), то это положение равновесия будет неустойчивым.
- ↑ Часто силу, пропорциональную смещению называют квазиупругой.
- ↑ Такая замена возможна, если производная от функции Fx(x) в точке равновесия отлична от нуля. Возможны такие редкие ситуации когда это условие не выполняется – один из них мы рассмотрим позднее.
- ↑ Принципиальную возможность такого построения решения мы показали при изучении кинематики.
Следующая страница
Всюду в нашей жизни мы встречаемся с колебательными движениями, начиная от качаний маятника, колебаний рессор и сотрясений кузова автомобиля или вагона поезда до страшных, разрушительных колебаний коры нашей планеты. Фабричные трубы и высокие здания колеблются под действием ветра, подобно полотну ножовки, зажатому одним концом в тисках. Правда, такие колебания не так уж велики. Амплитуда колебаний вершины Эйфелевой башни в Париже (высотой 300 м) при сильном ветре около 50 см.
Колебания! Наш взгляд падает на маятник стенных часов. Неугомонно спешит он то в одну, то в другую сторону, своими ударами как бы разбивая поток времени на точно размеренные отрезки. «Раз-два, раз-два», — невольно повторяем мы в такт его тиканью. Качание влево и обратно вправо, в исходное положение, составляет полное колебание маятника, а время одного полного колебания называют периодом колебания. Число колебаний тела в секунду называется частотой колебания.
Изучение колебаний начинается с изучения движения простого нитяного маятника, который вы легко можете изготовить, подвесив небольшой металлический шарик на нитку. Уменьшая мысленно размеры шарика до материальной точки, а нити приписывая идеальные свойства: невесомость, абсолютную гибкость и отсутствие трения, мы придаем к теоретическому, так называемому «математическому маятнику».
Период колебания маятника выражается формулой 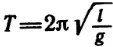
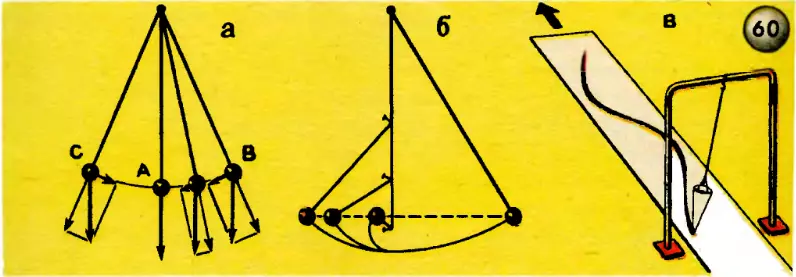
Как объяснить движение маятника, которые повторяются с одним и тем же периодом и могли бы продолжаться вечно, если бы маятник не встречал сопротивления движению в виде трения и не совершал бы работы, преодолевая это сопротивление? Очевидно, движение маятника происходит за счет сообщения ему энергии. Когда мы отводим маятник от вертикального положения, то сообщаем ему некоторый запас потенциальной энергии. Когда маятник опускается из точки B в точку A (рис. 60, а), потенциальная энергия, запасенная при подъеме переходит в кинетическую. Скорость маятника увеличивается, но не равномерно, потому что сила, сообщающая ускорение, уменьшается. В точке A скорость маятника будет наибольшей, поэтому маятник не может остановиться в этой точке, вследствие инерции он будет продолжать движение. Поскольку шарик привязан к нити, то подниматься в точку C он будет по дуге окружности. Высота подъема равна высоте опускания маятника. Это подметил еще Галилей в своем опыте, известном под названием «маятник Галилея» (рис. 60, б). Вбив по одной вертикальной линии, проходящей через положение равновесия маятника, гвоздики на различной высоте и пуская маятник, он подметил, что, обогнув гвоздик, маятник поднимался вправо на такую же высоту, с какой был опущен.
Колебания маятника — пример на закон сохранения энергии.
Колебания маятника — это гармонические колебания.
Что такое гармонические колебания, попробуем выяснить на опыте.
Подвесим воронку, склеенную из плотной бумаги и наполненную сухим, просеянным через частое сито песком, как показано на рисунке 60, в. Под воронку положим длинную полосу картона, выкрашенного в белый цвет. Пустив воронку качаться, как маятник, будем двигать картонную полоску равномерно в направлении, перпендикулярном к плоскости качания маятника. Высыпающийся из воронки песок «запишет» на картоне волнообразную линию, называемую синусоидой. Колебания, происходящие по закону синуса, называются синусоидальными или гармоническими. Происхождение слова «гармонический» уходит в даль веков, в историю Древней Греции, к учению Пифагора, искавшего начало всех начал в числах и учившего, что порядок и красота Вселенной основаны на числах.
Рассмотрев внимательно синусоиду, образованную на картоне, вы заметите, что песок ложится неодинаковой толщиной: чем ближе к вершине или впадине синусоиды, тем гуще насыпан песок. Это свидетельствует о том, что скорость маятника в этих точках была меньше, обращаясь в нуль в самых верхних и самых нижних точках кривой, т. е. в точках, где маятник менял свое движение на обратное. Среднее положение маятник проходил с максимальной, накопленной во время падения скоростью и потому оставлял тонкий след.
Большое значение при изучении колебательных процессов имеет понятие «фаза».
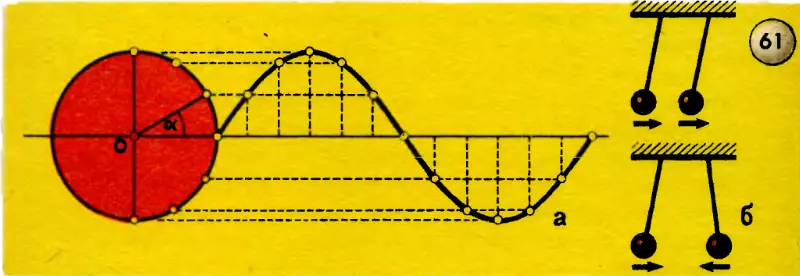
Фаза — слово греческое, в переводе на русский язык означает «проявление». В физике этим словом характеризуют стадию (ступень) развития периодического процесса, например: начало его, максимум развития, минимум и т. д. Однако такого определения фазы, как физической величины, недостаточно. Надо знать, как ее можно измерить. Для этого рассмотрим прием графического построения синусоиды (рис. 61, а). Из точки O как из центра опишем окружность и на продолжении горизонтального диаметра проведем горизонтальную линию (ось синусоиды). Представим, что по этой окружности равномерно вращается точка. Проекция радиуса-вектора, проходящего через последовательные положения точки, дадут нам значения соответствующих ординат точки синусоиды, а угол поворота радиуса вектора при этом, считая от горизонтальной оси против часовой стрелки, будет характеризовать положение точки на окружности, т. е. характеризовать стадию развития процесса. Этот угол называется фазовым углом или просто фазой. На рисунке 61, б показаны два маятника: вверху в одинаковых фазах, внизу в противоположных фазах колебания.
Маятник или другая колебательная система, приведенная в движение и предоставленная самой себе, совершает, как говорят, свободные колебания.
Предоставленный самому себе маятник будет продолжать качаться, но размахи его, амплитуды колебания, будут становиться все меньше и меньше, колебания будут затухать. Движение колеблющегося маятника переменное: то ускоренное, то замедленное, но это движение и не равномерно переменное. Как видно из чертежа, сила, сообщающая маятнику ускорение, уменьшается по мере уменьшения угла отклонения маятника от вертикального положения. В пружинном маятнике сила упругости растянутой или сжатой пружины непостоянна и сообщаемые маятнику ускорения тоже непостоянны. Такая зависимость ускоряющей силы от расстояния колеблющейся точки до положения равновесия является основным признаком гармонического движения. Гармоническими колебаниями называют поэтому колебания, вызванные силой, возрастающей пропорционально отклонению от положения равновесия. Колебания маятника можно считать гармоническими лишь при небольших отклонениях маятника от положения равновесия, не больших 10°.
В практике часто бывает необходимо поддержать колебания, не давать им затухать. Ясно, что для этого придется подводить к колеблющемуся телу энергию извне. В тех случаях, когда система приводится в колебательное движение действием какой-нибудь внешней, изменяющейся по модулю силы, мы будем иметь дело не со свободными, а с вынужденными колебаниями. Такие колебания, навязанные системе извне, будут происходить с частотой изменения силы, вызывающей эти колебания. Например, колебания фундамента двигателя являются вынужденными и происходят с частотой колебаний двигателя.
Непериодические изменения внешней силы, конечно, отражаются на частоте колебаний. Так, записанная на граммофонной пластинке речь или музыка повторятся мембраной патефона, приходящей в колебания с меняющейся частотой, а значит, воспроизводящей звуки различной высоты и громкости. Эти колебания вызваны толчками, которые получает иголка, двигаясь по дорожке звукозаписи. Если у вас есть граммофонная пластинка, то вы можете воспроизвести записанную на пластинке музыку или речь, приставив к равномерно вращающейся пластинке открытку или листок плотной бумаги.
В том случае, когда частота изменения внешней силы совпадает с собственной частотой колебательной системы, происходит увеличение амплитуды колебаний этой системы. Так, периодически подталкивая качели, в такт их собственным колебаниям, мы можем очень сильно раскачать их. Такое явление носит название резонанса и имеет огромное значение в технике. Настраивая радиоприемник на определенную частоту, вы приводите его в резонанс с радиовещательной станцией.
Опасные последствия, которые могут быть вызваны резонансом (разрушение мостов, потолочных перекрытий, фундаментов), описаны в любом учебнике физики.
Остановимся еще на одном виде колебаний — автоколебаниях. Так называются колебания, происходящие с собственной частотой колеблющейся системы, но под действием не переменной, а постоянной силы. Когда скрипач равномерно ведет смычок по струне скрипки, струна совершает собственные автоколебания, дающие звук определенного тона. Когда анкер часов своими палетами (зубьями) соприкасается с зубьями ходового колеса, они подталкивают их в направлении движения. В результате маятник колеблется с собственной частотой, зависящей только от его длины.
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
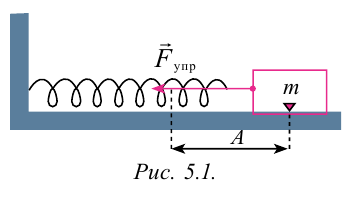
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Гармонические колебания в физике — формулы и определение с примерами
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 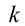
Если груз, который находится в равновесии, потянем вправо на расстояние 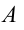
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
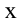
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 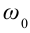
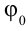
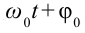
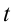
Из математики известно, что 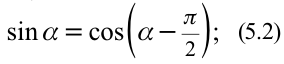
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 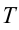

б) частота колебания 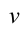
Единица 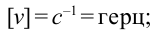
c) циклическая частота 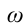
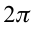
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 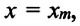
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 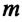
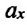
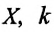
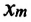
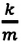
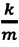
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 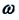
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 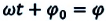
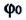
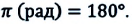
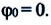

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 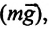
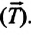
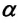
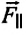
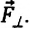
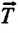
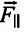
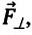
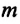
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 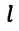
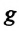
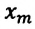
Для данной колебательной системы отношение 

Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 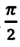
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 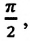
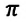
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 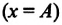
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 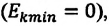
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 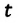
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
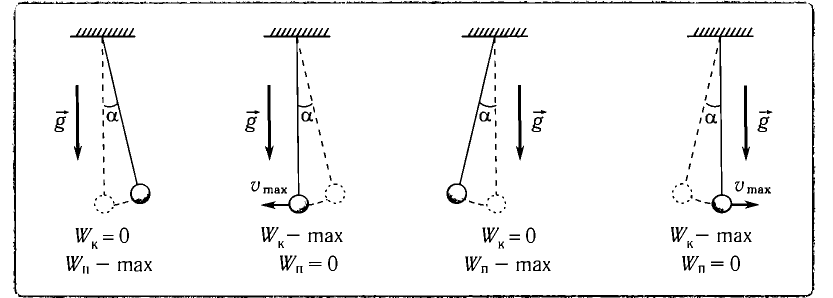
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
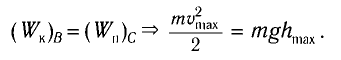
Отсюда найдем модуль максимальной скорости маятника:
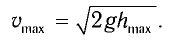
Высоту 
Если колебания малые, то 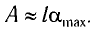
Подставив выражение для 
Подставляя выражения для 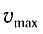

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 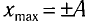
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 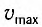
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 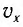
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 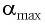
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 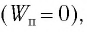
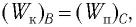
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 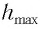
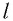
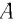
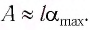
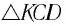
или
Подставив выражение (3) для 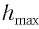
Подставляя выражения (3) для 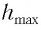
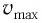
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 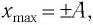
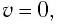
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 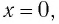
где 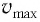
В положениях между крайними точками полная энергия
С учетом выражений для координаты 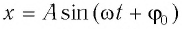
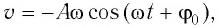
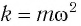
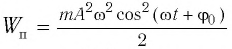
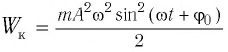
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 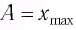
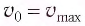
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 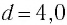
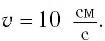
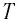
Дано:
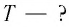
Решение
По закону сохранения механической энергии
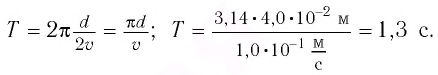
Ответ:
Пример №2
Груз массой 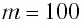
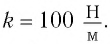
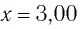
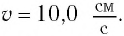
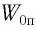
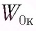
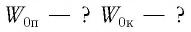
Решение Потенциальная энергия груза: 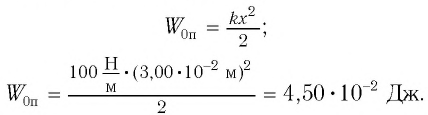
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда 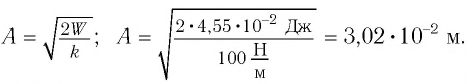
Циклическая частота: 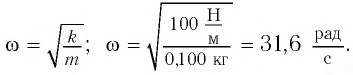
В начальный момент времени 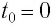
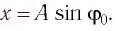
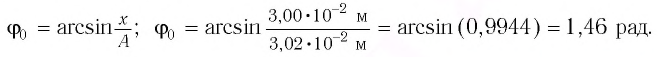
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение гармонических колебаний
п.1. Гармонические колебания как простейший периодический процесс
Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.
Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10 -14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·10 15 с
Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sint) и (cost) с периодом (T=2pi).
Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:
Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac<20><10>=4pi text <(рад/с)>end Получаем закон колебаний: (x(t)=5cos(4pi t))
п.2. Перемещение, скорость и ускорение при гармоническом движении
Пусть (x(t)) — координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acosomega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-Aomega sinomega t=Aomega cosleft(omega t+fracpi 2right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $$ v_m=Aomega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x»(t)=-Aomega^2 cosomega t=Aomega^2 cos(omega t+pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $$ a_m=Aomega^2 $$ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:
Из уравнения для ускорения получаем: $$ x»(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $$ Откуда следует:
Решением этого уравнения в общем виде будут: $$ x(t)=Asin(omega t+varphi_0) text<или> x(t)=A cos(omega t+varphi_0) $$ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.
п.3. Примеры
Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?
 |
Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения. |
По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end Уравнение движения грузика: $$ x»(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt<frac km>)
Общее решение уравнения: (x(t)=Acosleft(sqrt<frac km>+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt<frac km>, a_m=Afrac km $$ Ответ: (omega=sqrt<frac km>)
Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?
 |
Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g. |
Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?
 |
LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем. |
Напряжение на конденсаторе (U_C(t)=frac). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac<triangle I><triangle t>). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin U_c(t)=varepsilon_L(t)Rightarrow frac=-LI'(t)Rightarrow frac+LI'(t)=0 end Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin frac+LQ»(t)=0 end Получаем уравнение гармонических колебаний: $$ Q»(t)=frac<1>Q(t)=0, omega=frac<1><sqrt> $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac<1><sqrt>t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac=fraccosleft(frac<1><sqrt>t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac)
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac<sqrt>sinleft(frac<1><sqrt>t+varphi_0right)=frac<sqrt>cosleft(frac<1><sqrt>t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac<sqrt>)
Ток опережает колебания заряда и напряжения на (fracpi 2)
http://www.evkova.org/garmonicheskie-kolebaniya-v-fizike
http://reshator.com/sprav/algebra/10-11-klass/uravnenie-garmonicheskih-kolebanij/