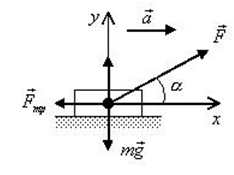
Enter the velocity before braking and the total stopping distance into the calculator to determine the Braking Acceleration.
- All Acceleration Calculators
- Braking Force Calculator
- Stopping Distance Calculator
- Brake Caliper Clamping Force Calculator
Braking Acceleration Formula
The following equation is used to calculate the Braking Acceleration.
Ab = V^2 / (2*SD)
- Where Ab is the Braking Acceleration (m/s^2)
- V is the velocity before braking (m/s)
- SD is the total stopping distance (m)
Braking acceleration is also often referred to as braking deceleration.
What are the units for Braking Acceleration?
The most common units for Braking Acceleration are m/s^2.
How to Calculate Braking Acceleration?
Example Problem:
The following example problem outlines the steps and information needed to calculate the Braking Acceleration.
First, determine the velocity before braking. In this example, the velocity before braking is determined to be 150 (m/s).
Next, determine the total stopping distance. For this problem, the total stopping distance is measured to be 10 (m).
Finally, calculate the Braking Acceleration using the formula above:
Ab = V^2 / (2*SD)
Inserting the values from above and solving the equation with the imputed values gives:
Ab = 150^2 / (2*10) = 1125 (m/s^2)
Перейти к содержимому
Задача №34. Ускорение при торможении и длина пути торможения автомобиля
Определить ускорение автомобиля при торможении и длину пути торможения, если автомобиль за время торможения равное 5 секундам снизил скорость с 10 метров в секунду до 5 метров в секунду.
Дано: v0=10 м/с; v1=5 м/с; t=5 с
Найти: a — ?; L — ?
Решение:
Ускорение при торможении определяем по формуле

Путь при торможении определяем по формуле

Ответ: ускорение автомобиля при торможении составило -1 метр в секунду в квадрате, путь при торможении равен 37,5 метрам
При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a
Задача «Разгон»
Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.
Решение.
Используем известную нам схему решения кинематических задач.
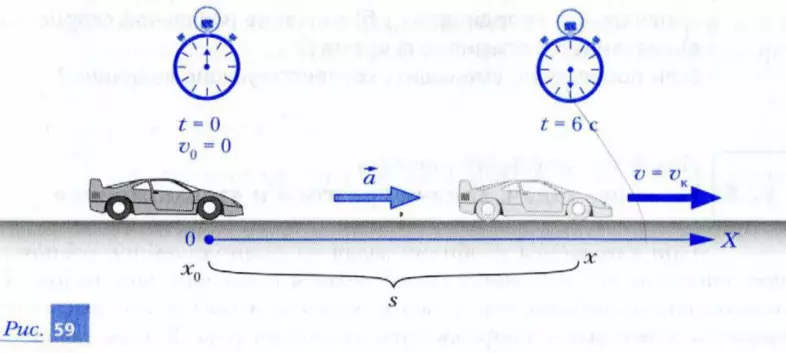
Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x0 = 0.
Шаг 3. По условию начальная скорость автомобиля v0 = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.
Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:
x = x0 + v0 · t + (a · t2) / 2 = 0 + 0 + (a · t2) / 2 = (a · t2) / 2.
Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:
v = v0 + a · t = 0 + a · t = a · t.
Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).
Шаг 5. Условие окончания разгона до скорости vк имеет вид:
v = vк.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = (a · t2) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = vк. (3) (условие окончания разгона)
Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:
vк = a · t,
a = vк/t; a = 30/6 = 5 (м/с2).
Подставив полученное значение a в уравнение (1), находим:
x = (a · t2) / 2 = (5 · 62) / 2 = 90 (м).
Ясно, что s = x — x0 = 90 — 0 = 90 (м).
Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.
Задача «Торможение»
Автобус движется со скоростью, модуль которой равен 20 м/с (72 км/ч). Водитель автобуса замечает на дороге кошку и нажимает на педаль тормоза. Определите длину тормозного пути автобуса, если модуль ускорения при торможении |a| = 4 м/с2.
Решение.
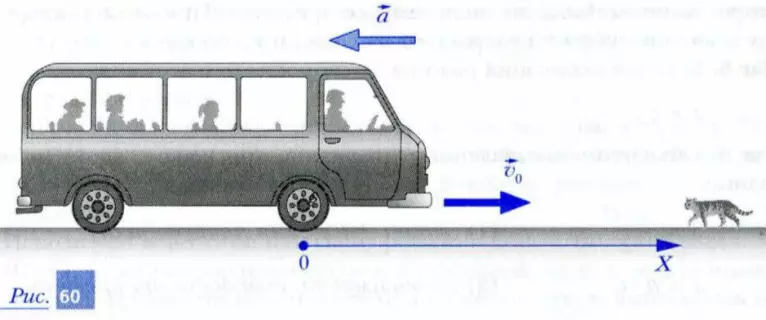
Шаг 1. Систему отсчета выберем так, как показано на рис. 60.
Шаг 2. Начальная координата автобуса x0 = 0.
Шаг 3. Значение начальной скорости автобуса v0 = 20 м/с.
Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:
x = x0 + v0 · t + (a · t2) / 2 = 0 + 20 · t — (4 · t2) / 2.
Внимание! Значение скорости автобуса уменьшается. Значит, направление вектора ускорения автобуса противоположно положительному направлению оси X. Поэтому мы подставили в формулу отрицательное значение ускорения (a = -4 м/с2). При этом направление вектора начальной скорости совпадает с положительным направлением оси X. Поэтому значение скорости v0 положительно. Такие же знаки у величин v0 и a будут и в шаге 4*.
Шаг 4* (новый). Зависимость значения скорости от времени имеет вид:
v = v0 + a · t = 20 — 4 · t.
Видно, что при отрицательном значении ускорения a = -4 м/с2 скорость автобуса со временем уменьшается. При этом за каждую секунду значение скорости изменяется на величину -4 м/с, т. е. уменьшается на 4 м/с.
Шаг 5. Запишем условие окончания торможения: v = 0, так как в искомый момент времени t автобус должен остановиться.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = 0 + 20 · t — (4 · t2) / 2, (1) (закон движения автобуса)
v = v0 + a · t = 20 — 4 · t, (2) (зависимость скорости от времени)
v = 0. (3) (условие окончания торможения)
Шаг 7. Решение уравнений. Чтобы найти тормозной путь, необходимо подставить в уравнение (1) время торможения автобуса. Эта величина нам неизвестна, но ее можно найти из уравнений (2) и (3). Для этого необходимо подставить в зависимость скорости от времени значение скорости в момент окончания торможения v = 0, после чего решить полученное уравнение:
20 — 4 · t = 0, t = 5 c.
Таким образом, автобус остановится через время t = 5 с.
Подставим найденное время торможения t = 5 с в уравнение (1) и найдем тормозной путь:
x = 20 · 5 — (4 · 52) / 2 = 50 (м).
Таким образом, длина тормозного пути автобуса равна 50 м.
Итоги
Если положительное направление оси X выбрать совпадающим с направлением движения тела, то все задачи на равноускоренное движение можно свести к двум типам:
1) задача «разгон» (a > 0, скорость тела увеличивается с течением времени);
2) задача «торможение» (a
Если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы, в течение каждого из которых тело движется только в одном направлении. При этом задача разделяется на несколько задач.
Упражнения
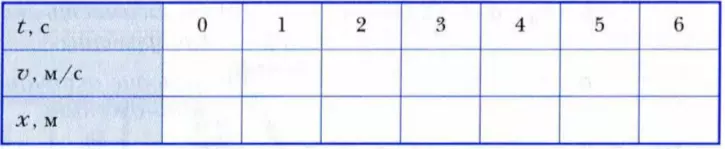
1. Заполните таблицу для разгоняющегося автомобиля, используя условия задачи 1 («разгон»). Как изменяются со временем: значение скорости; координата разгоняющегося автомобиля?
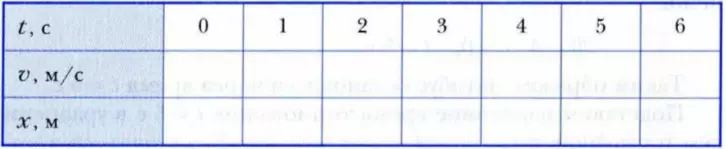
2. Заполните таблицу для тормозящего автобуса, используя условия задачи 2 («торможение»). Ответьте на вопросы: как изменяются со временем: значение скорости; координата тормозящего автобуса?
3. Найдите координату x автомобиля (см. рис. 57) в моменты времени 3, 5 и 8 с, если его начальная координата x0 = 30 м, значение начальной скорости v0 = 10 м/с, а значение ускорения a = 3 м/с2.
4. Решите задачу 2 («торможение») в общем виде. Представьте полученный ответ в виде
s = v02 / (2 · a).
Проведите анализ полученного ответа. Определите тормозной путь автобуса, если: а) v0 = 16 м/с; б) v0 = 115,2 км/ч.
5. Найдите путь, пройденный автомобилем, движение которого задано в упражнении 3, за промежуток времени от t1 = 2 с до t2 =5 с.
6. Два мотоциклиста, двигавшиеся прямолинейно, начинают одновременно тормозить перед светофором и так же одновременно останавливаются, проехав расстояние s = 100 м. Первый мотоциклист перед торможением двигался со скоростью, имеющей значение v1 = 72 км/ч, второй – со скоростью, имеющей значение v2 = 108 км/ч. Найдите значения ускорений мотоциклистов.
Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.
Кинематические характеристики движения
Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь — это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S — это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).

Скорость или как часто ее называют линейная скорость — это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).
Ускорение — третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с2).
Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.
Связь скорости и ускорения
Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:
v = v0 + a * t.
Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени. Поскольку v0 и a являются постоянными величинами, а v и t — это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v0), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).
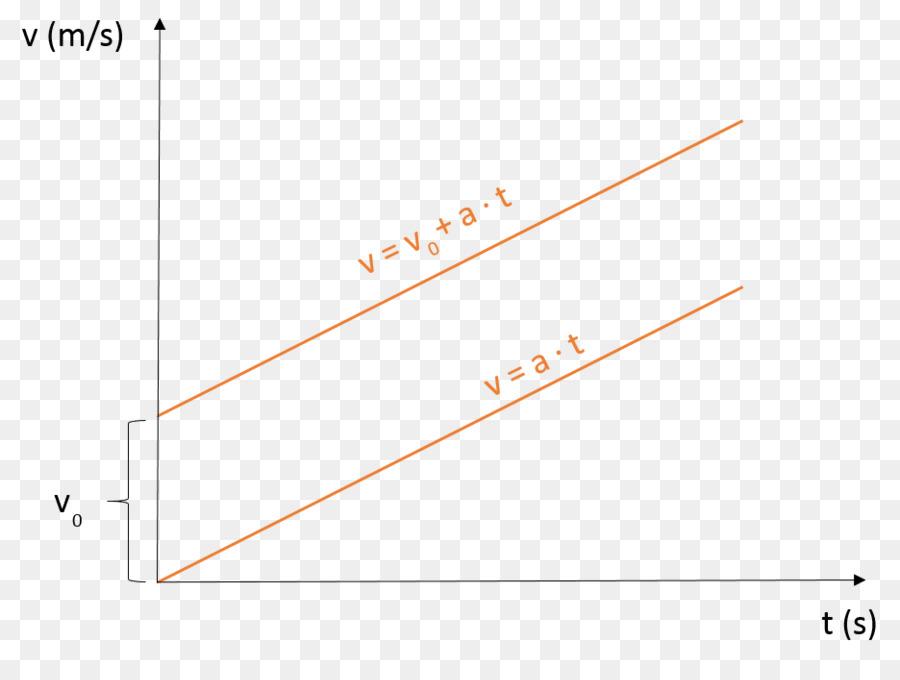
На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:
v = v0 — a * t.
Этот вид движения называется прямолинейным равнозамедленным.
Формулы пройденного пути
На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:
S = v0 * t + a * t2 / 2.
Первый член соответствует равномерному движению без ускорения. Второй член — это вклад в пройденный путь чистого ускоренного движения.
В случае торможения движущегося объекта выражение для пути примет вид:
S = v0 * t — a * t2 / 2.
В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.
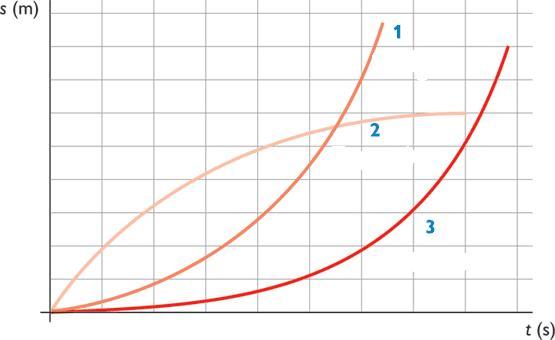
Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.
Далее в статье решим три разные задачи на использование приведенных формул.
Задача на определение времени движения
Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?
Расстояние, которое авто за 20 секунд пройдет, будет равно:
S1 = a * t12 / 2.
При этом скорость, которую он наберет за 20 секунд, равна:
v = a * t1.
Тогда искомое время движения t можно вычислить по следующей формуле:
t = (S — S1) / v + t1 = (S — a * t12 / 2) / (a * t1) + t1.
Здесь S — расстояние между A и B.
Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.
Задача на расчет пути торможения
Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.
Тормозной путь S можно рассчитать по следующей формуле:
S = v0 * t — a * t2 / 2.
Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:
v0 — a * t = 0;
a = v0 / t.
Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:
S = v0 * t — v0 * t / 2 = v0 * t / 2.
Подставляем значения из условия и записываем ответ: S = 145,8 метра.
Задача на определение скорости при свободном падении
Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?
Искомую скорость можно рассчитать по формуле:
v = g * t.
Где g = 9,81 м/с2.
Время падения тела определим из соответствующего выражения для пути S:
S = g * t2 / 2;
t = √(2 * S / g).
Подставляем время t в формулу для v, получаем:
v = g * √(2 * S / g) = √(2 * S * g).
Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ — тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме