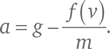Как найти скорость установившегося движения

Установившимся
(стационарным)
движением называется такое, при котором
скорость течения и все основные параметры
потока (давление, плотность и т.д.) не
изменяются с течением времени. В этом
случае время в число аргументов не
входит и скорость, например, является
функцией только координат:
и при этом

(1.4)

Примерами
установившегося движения могут служить:
движение воды в канале при постоянном
уровне воды, истечение жидкости из
отверстия при постоянном напоре,
истечение из водопроводного крана при
постоянном давлении и т.д.

Неустановившимся
(нестационарным)движением жидкости
называется такое, при котором в каждой
точке скорость течения и все остальные
параметры потока изменяются со временем.

Для
вектора скорости, например, в число
аргументов будет входить время:
и

(1.5)

Примерами
неустановившегося движения являются:
движение воды в реке при изменении
уровня в ней (в паводок), истечение через
отверстие в резервуаре при его опорожнении
и т.д. В некоторых случаях характер
движения будет зависеть от выбора
системы координат. Так, в координатной
системе, связанной с кораблем, плывущим
по реке (для человека, стоящего на палубе)
система волн и весь процесс обтекания
корабля будет установившимся, в то время
как в неподвижной системе (для человека,
стоящего на берегу) процесс волнообразования
при прохождении корабля будет
неустановившимся. Заметим, что изучение
установившегося движения гораздо проще,
чем неустановившегося.

1.3. Линии тока. Свойство линий тока

Линией
тока называется кривая, в каждой точке
которой вектор скорости в данный момент
времени направлен по касательной.

В случае
установившегося движения линии тока
совпадают с траекториями частиц жидкости.

Свойство
линий тока: линии тока не пересекаются
ни сами с собой ни с другимилиниями
тока.

П

Рис.
1.3

Рис.
1.4

а)

б)

рименим
способ доказательства от противного,
т. е. допустим, что линии токаIиIIпересеклись в точке
О, рис.1.3. Тогда, проведя касательные к
кривымIиIIв точке О, видим, что в этой точке частица
жидкости должна двигаться в разных
направлениях, что невозможно. Следовательно,
исходное допущение неверно, т.е. линии
тока не пересекаются ни сами с собой,
ни друг с другом.

Если
траектория фиксирует положение во
времени только одной частицы, то линия
тока в один и тот же момент времени
указывает направление скоростей многих
частиц. Иногда используется представление
о линии отмеченных частиц; это линия,
на которой находятся все частицы,
прошедшие через одну какую-либо точку
в пространстве. Линию отмеченных частиц
можно получить, если в поток жидкости
поместить трубку и вводить в неё краску.

Как
следует из определения, линия тока есть
такая линия, в каждой точке которой
нормальная составляющая скорости равна
нулю, т е. через линию тока нет перетекания.
Поэтому между двумя линиями тока
количество протекающей жидкости
постоянно и для несжимаемой жидкости
в местах, где линии тока сближаются,
величины скорости увеличиваются, и
наоборот, там где они расходятся, скорости
убывают. Если через поверхность
обтекаемого тела жидкость не протекает,
то эта поверхность есть поверхность
тока (поверхность, состоящая из линий
тока). Для плоского обтекания, рис. 1.4,
а, это будет линия тока О – О, которая в
отличие от других называется нулевой
линией тока. Совокупность линий тока
дает картину течения в данный момент
времени, что часто используется для
наглядного изображения особенностей
потока. Например, на рис. 1.4, б с помощью
линий тока изображена картина обтекания
плоской пластины, установленной
перпендикулярно потоку. В случае плоского
(двумерного) течения возможно элементарным
способом получить дифференциальное
уравнение линии тока. Для этого учтём,
что при течении в плоскости xoy
проекции вектора скорости определяются
так

.

Исключая
из этих равенств dt, получим
дифференциальное уравнение линии тока

.

С помощью
этого уравнения, если известны компоненты
вектора скорости
и,
возможно найти уравнение линии тока.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лекция N8

Основные режимы движения механизма.

Как отмечалось в предыдущей лекции №7 , процесс движения машины (механизма) в общем случае состоит из трех фаз (см. рис. 8.1):

1. Разгона; 2. Установившегося движения; 3. выбега.

Рис. 8.1

Фаза разгона характеризуется увеличением скорости начального звена. Это наблюдается при пуске машины в ход (см. рис. 8.1 режим I) или при переходе ее с меньшей скорости на большую (режим II)  ().

         Во время выбега скорость звена приведения уменьшается. Это происходит при остановке механизма (режим ), торможении или при переходе его с большей скорости на меньшую (режим ).

Рекомендуемые материалы

         Многие механизмы вообще не работают в цикловом режиме. Это характерно для целого ряда приборов. Их механизмы переходят из одного положения в другое, не совершая при этом замкнутого цикла (режим ).

При установившемся режиме скорость начального звена изменяется периодически. Причиной является периодический характер действия сил и моментов, приложенных к механизму, а также периодические изменения приведенного момента инерции механизма (). Среднее значение угловой скорости поддерживается на постоянном (среднем) уровне (режим III на рис. 8.1)

Исследование установившегося режима движения.

 Установившемся движением называется такое движение, при котором скорость начального звена является периодической функцией времени.

График  или  имеет вид периодической кривой изображенной на рис. 8.2.

Рис. 8.2

Как видно, из рис. 8.2 угловая скорость  колеблется относительно некоторого среднего значения , причем характер изменения угловой скорости периодически повторяется.

Угловая скорость начального звена может быть определена по формуле:

Время, по истечение которого скорость начального звена принимает свое первоначальное значение после чего характер ее изменения повторяется, называется временем цикла, или сокращенно циклом.

Установившееся движение имеет место только в том случае, если, т.е. сумма работ за цикл всех сил, приложенных к механизму, равна нулю.

Так как , то . Из этого заключения следует, что приращения кинематической энергии за цикл не происходит () и угловая скорость в начале и конце цикла одинакова.

При оценке изменения угловой скорости при установившемся режиме вводят два критерия:

1. средняя (номинальная) скорость

                                                                                              (8.1)

2. коэффициент неравномерности вращения

                                                                                   (8.2)

Проектируя определенный класс машин, конструктор должен обеспечивать для этого класс машин колебание «»  в данных пределах, которые выработаны многолетней инженерной практикой.

Совместны решения уравнений для  и  дает значения  и :

                                                                                            (8.3)

                                                                                            (8.4)

Отличие  и  от  составляют , т.е. обычно не более .

В установившемся режиме работают очень многие машины (станки, прессы, прокатные станы, текстильные, полиграфические и многие другие машины). Колебания угловой скорости ухудшают рабочий процесс машины, вызывают дополнительные динамические нагрузки, вследствие чего снижается долговечность и надежность машин, а иногда и качество продукции.

Поскольку колебания скорости, обусловленные периодическими воздействиями сил, полностью устранить нельзя, то нужно по возможности сократить их размах. Иными словами, величину коэффициента  надо сделать приемлемо малой.

Рассмотрим какими средствами можно решить эту задачу. Все звенья механизма обладают инертностью. Как известно из физики, это свойство состоит в том, что чем инертнее материальное тело, тем медленнее происходят изменения его скорости, вызываемые действием приложенных сил. Поэтому, чтобы получить вращение главного вала машины с циклической неравномерностью, не превышающей требуемой величины, инертность этого вала со всеми жестко связанными с ним деталями надо сделать достаточно большой. Для этого на главном валу машины надо закрепить добавочную массу, выполненную в виде колеса с развитым ободом и называемую маховиком. Его момент инерции должен быть таким, чтобы неравномерность вращения главного вала машины не превышала заданных пределов.

Как отмечалось в предыдущих лекциях:

Воздействие на  через  связано со значительными трудностями, а через  это сделать достаточно просто. В  входят моменты инерции звеньев связанных с главным валом (начальным звеном) постоянным передаточным отношением, в том числе и маховик.

Подбирая момент инерции дополнительной маховой массы (маховика), можно придать величине  такое значение, при котором вал звена приведения будет вращаться с допустимой степенью неравномерности.

Итак, основное назначение маховика состоит в ограничении колебаний угловой скорости главного вала машины в пределах, определяемых значением коэффициента неравномерности . Определение момента инерции маховика по заданным условиям движения (т.е. по заданному значению ) производится в процессе проектирования машины и составляет одну из задач ее динамического синтеза. Подчеркнем при этом, что свое основное назначение маховик может выполнить только при установившемся режиме.

Расчет маховых масс по методике Н.И. Мерцалова.

Решим обе задачи – и динамический синтез и динамический анализ — наиболее простым и наглядным методом Мерцалова, основанным на применении диаграммы . Сначала выполним динамический синтез, составив, прежде всего расчетную формулу для определения приведенного момента инерции I группы звеньев, необходимого для обеспечения заданного значения .

Для динамической модели:

Тогда используя уравнение теоремы об изменении кинетической энергии  можно записать:

(с достаточной степенью точности)

         Принибрегая маленькими значениями  и членами с этими значениями, т.е. , получим:

т.к. , то с учётом этого можно записать:

— формула Н.И. Мерцалова

                                             или                                       (8.5)

Формула 8.5 предназначается для расчета маховых масс по Мерцалову Способ Мерцалова основан на определении кинетической энергии всех звеньев механизма и последующим выделением из этой кинематической энергии той ее части, которая приходится только на звено приведения (модель) и на звенья, связанные с ним постоянным передаточным отношением. После этого легко определить искомое значение наибольшего периода кинетической энергии  

, где , тогда

                                                                                                        (8.6)

так как кинетическая энергия механизма                                  (8.7)

тогда  (8.8),                                а             (8.9)

Рис. 8.3

Проиллюстрируем сказанное графиками. Пусть известны диа­грамма  (верхняя кривая на рис. 8.3, а, построенная от­носительно оси ) и диаграмма  (рис. 8.3, б) кинетической энергии группы II звеньев, т. е. тех, приведенные моменты инерции которых переменны. Согласно уравнению (8.6), прибавим к сумме работ  значение кинетической энергии  всего механизма в начале цикла. Для этого сместим ось  на величину  вниз (рис.8.3, а), после чего верхняя кривая на рис. 8.3, а будет относительно оси  изображать кинетическую энергию Т всего механизма. Вычтем, согласно уравнению (8.6), из кинетической энергии Т кинетическую энергию  и получим нижнюю кривую на рис.8.3, а. Нижняя кривая, отнесенная к оси , и является кривой кинетической энергии . Отметим на этой кривой точку максимума Q и точку минимума N и по ним опреде­лим наибольший перепад

кинетической энергии , необходимый для подсчета  по уравнению (8.5).

Обратим внимание, что для подсчета  по формуле (8.5) надо знать не величину кинетической энергии  , а ее наибольшее измене­ние . Но  не зависит от начального значения , и, следовательно, для определения  не нужно знать числового значения , т. е. не нужно выявлять положение сдвинутой оси абсцисс .

Составим порядок определения момента инерции маховика по методу Мерцалова графическим способом:

· приведение сил и моментов; построение диаграммы суммар­ного приведенного момента ;

· построение диаграммы  способом графического интегрирования;

· приведение масс; построение диаграммы ;

· определение кинетической энергии по формуле  и переход к диаграмме ;

· построение диаграммы кинетической энергии  по уравне­нию (8.6) (без выявления положения сдвинутой оси абсцисс) и опре­деление ;

· подсчет по уравнению (8.5) и определение момента инер­ции маховика.

В таком же порядке нужно вести расчет и численным способом с применением ЭВМ.

На рис. 8.5 изображены графики, выполненные для расчета маховика по методу Мерцалова для машинной установки, состав­ленной из ДВС и электрогенератора (см. рис. 8.4, а). Механические характеристики, необходимые для расчета, заданы в функции пере­мещения (см. рис. 8.4, б, в) поскольку вал генератора вращается практически равномерно. Начальным звеном назначим коленчатый вал ДВС — звено 1. Рассмотрим особенности расчета.

Сначала надо сделать приведение движущей силы  и для одного полного цикла получить зависимость . Так как маховик может выполнить свое основное назначение только в условиях установившегося режима, то при его расчете непременно должно быть соблюдено основное энергетическое уравне­ние: . Это уравнение обусловливает обязательное соотношение между работами движущих сил и сил сопротивления, а именно: . Отсюда, учитывая, что , получим .

Подсчитав , нужно определить  (рис. 8.5). Признаком установившегося режима на рис. 8.5, а является то, что площадки над осью абсцисс и под ней равновелики, а на рис.8.5,  — то, что ордината кривой  в конце цикла равна нулю.

Так как механизм во взятом примере такой же, как и рассмотренный в лекции 7, то, используя формулы (7.22 – 7.25), заключаем, что в состав группы I входят звенья 1 и 4, а в состав группы II —  звенья 2 и 3. График приведен­ного момента инерции  представлен на рис. 8.5, в.

Кинетическая энергия  определяется уравнением . Пока задача динамического синтеза не завершена, точное текущее значение  еще не известно. Но вследствие малости коэффициента неравномерности справедливо приближенное равенство . Поэтому можно принять . Так как , то график  представляет собой одновременно и график , но выполненный в другом масштабе (рис. 8.5, в); соотношение между масштабами таково: . Таким образом, метод Мерцало­ва не является, строго говоря, точным, но вследствие малости ошибки вполне пригоден для практических расчетов.

Поскольку  подсчитано не вполне точно, график  (рис. 8.5, б и г), а вместе с ним и наибольший перепад  кинетической энергии (рис. 8.5, г) содержат некоторую ошибку. При  можно сделать уточнение величины  по формуле, предложенной Д. М. Лукичевым:   (см.: Лукичев Д. М. Расчет маховика машины// Вопросы теории механиз­мов и машин, 1953. № 23). В этой формуле  и  — значения кинетической энергии  в тех положениях п и q механизма, в которых кинетическая энергия  проходит свои крайние экстремумы; в уравнение (8.5) следует подставить .

Рис. 8.6

Определив , по уравнению (8.5) динамического синтеза при установившемся режиме подсчитываем  а затем . Во многих случаях момент инерции махо­вика  преобладает над ос­тальными моментами инерции I группы звеньев. Поэтому вся­кие изменения кинетической энергии  происходят прежде всего за счет изменений кинети­ческой энергии маховика.

Рассмотрим роль маховика. В процессе расширения газов. (см. рис. 8.4, в) ДВС вырабатывает энергии больше, чем потребляет генератор. Избыток ее идет на увеличение  (участок NQ на рис. 8.5, г), т. е. прежде всего на увеличение кинетической энергии маховика. Во время процесса сжа­тия газов ДВС сам потребляет энергию на совершение работы сжатия. Генератор в это время также продолжает забирать энергию с вала ДВС. Оба эти расхода энергии возмещаются за счет уменьше­ния  (участок QN на рис. 8.5, г), т.е. в основном за счет уменьшения кинетической энергии маховика.

Таким образом, маховик то накапливает кинетическую энергию, когда работа двигателя оказывается в избытке, то отдает часть ее. Чем больше  (а следовательно, и ) тем выше аккумулирующая способность маховика, тем меньше будут колебания  при колеба­ниях потока энергии, тем равномернее будет вращаться вал маши­ны, что видно из уравнения (8.5), решенного относительно :

                                                                                                        (8.10)

Аккумулирующая способность маховика используется не только для обеспечения допустимой неравномерности хода машин. Так, в автомашинах маховик содействует троганию автомобиля с места. Маховики непременно применяются в машинах ударного дейст­вия — молотах, прокатных станах и др., — помогая электродвига­телю во время удара. В настоящее время разрабатываются проекты транспортных машин, в которых маховик — механический аккуму­лятор — должен использоваться как экологически чистый и авто­номный источник энергии.

Выше было изложено решение задачи динамического синтеза, состоящей в определении момента инерции маховика , обес­печивающего требуемое условие движения, заданное коэффициен­том неравномерности . Теперь решим обратную задачу — задачу динамического анализа. При установившемся режиме известны все характеристики механизма, в том числе и , требуется определить закон движения, а затем и фактическое значение . Решение этой задачи также основано на применении диаграммы , которая строится по методу Мерцалова (рис. 8.5).

Проведем через начальную точку О» кривой  ось (показана на рис.8.5, г штрихами). Относительно этой новой оси кривая изобразит изменение кинетической энергии , которое выражается так:

Так как неравномерность вращения начального звена заведомо мала, то можно приближенно принять . Тогда, обозначив , получим

Но . Следовательно, при установившемся движении с малым значением коэффициента неравномерности  изменение кинетической энергии  приблизительно пропорционально изменению  угловой скорости начального звена. Поэтому кривая на рис. 8.5, г одновременно изображает как , так и , но в разных масштабах; соотношение между масштабами таково: . График   изображен на рис. 8.6.

Коэффициент неравномерности  определяют по формуле:

Угловое ускорение  начального звена при установившемся движении подсчитывают по уравнению

в котором . Значения  и  берут с соответствующих диаграмм (рис.8.5, а, в); . Производную  определяют графическим или численным дифференцированием функции (поскольку ) так как указано в лекции 7. В величинах  и  — нужно учитывать знак.

Угловое ускорение начального звена можно также выразить следующим образом:

Тогда  определяют по диаграмме  (рис. 8.6), применяя графи­ческое или численное дифференцирование.

Контрольные вопросы к лекции N8

«53 Знакочередующиеся (знакопеременные) ряды» — тут тоже много полезного для Вас.

1. Как оценивать неравномерность хода машины? Как её можно уменьшить?

2. Какие факторы вызывают периодические и непериодические колебания входного звена машины?

3. Сформулируйте основное назначение маховой массы (маховика)?

4. Какова цель установки маховика в машине? Чем следует руководствоваться при выборе места установки маховика в машине?

5. В каких случаях маховик необходим и когда он не требуется?

6. Выведите формулу для расчёта дополнительных маховых масс при постоянном приведённом моменте инерции машины?

Чтобы понять, как наблюдения за падающими телами привели Аристотеля к его теории падения тел, мы можем воспользоваться физическим принципом, Аристотелю неизвестным, – Вторым законом Ньютона. Он говорит нам, что ускорение a тела (темп возрастания его скорости) равно частному от деления полной силы F, действующей на тело, на его массу m:

На тело, падающее в воздухе, действуют две основные силы. Одна из них – сила тяготения, пропорциональная массе падающего тела:

F_т = mg.

Здесь g – постоянная величина, не зависящая от того, какое именно тело падает. Оно обозначает ускорение свободного падения тела в вакууме и вблизи земной поверхности, приблизительно равное 9,8 м/с за секунду. Вторая сила – сопротивление воздуха. Она выражается функцией f (v), значение которой пропорционально плотности воздуха, увеличивается с ростом скорости и зависит от формы и размера тела, но не зависит от его массы:

F_в = ?f(v) = kv.

В этой формуле знак минуса для силы сопротивления воздуха подставлен, потому что мы рассматриваем ускорение, направленное вертикально вниз, а для вертикально падающего тела сила сопротивления воздуха направлена вверх. Например, для тела, падающего сквозь среду значительной вязкости, ее сопротивление пропорционально скорости тела:

f(v) = kv.

В этой формуле k – положительная константа, которая зависит от размера и формы тела. В то же время, если мы рассмотрим, например, метеороид или ракету, входящую в разреженные верхние слои атмосферы, то будет работать другая формула:

f(v) = Kv?,

где K – другая положительная константа.

Подставив в формулу для полной силы, действующей на падающее тело, F = F_т + F_в выражения для сил тяготения и сопротивления и заменив затем полученной суммой множитель силы во Втором законе Ньютона, получаем:

Когда тело только-только отпустили и оно лишь начало падать, его скорость еще ничтожно мала, поэтому сила сопротивления воздуха не действует, и оно просто летит вниз с ускорением, равным g. По мере падения его скорость растет и сопротивление воздуха начинает уменьшать ускорение падения. В конце концов скорость становится такой, что слагаемое – f (v)/m сравнивается по модулю со слагаемым g в формуле выше и ускорение падает до близкой к нулю величины. Эта скорость называется установившейся скоростью падения и определяется как корень уравнения

f (v_уст) = gm.

Аристотель нигде не упоминал установившуюся скорость падения, но та скорость, которую можно определить по этой формуле, характеризуется теми же свойствами, которые он приписывал скоростям падающих тел. Поскольку f (v) – монотонно возрастающая функция от v, то установившаяся скорость возрастает с ростом массы m. В особом случае, когда f(v) = kv, установившаяся скорость падения прямо пропорциональна массе и обратно пропорциональна коэффициенту сопротивления:

Но в общем случае зависимость скорости падающих тел от времени может быть иной. Так или иначе, тяжелые тела приобретают присущую им установившуюся скорость только после продолжительного падения.