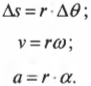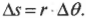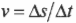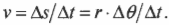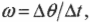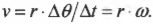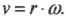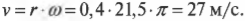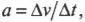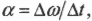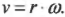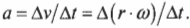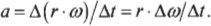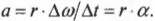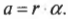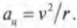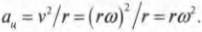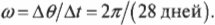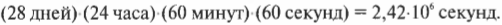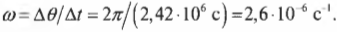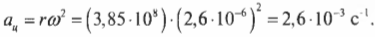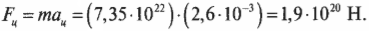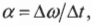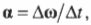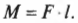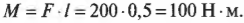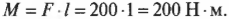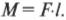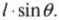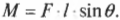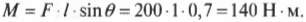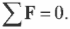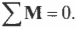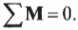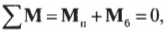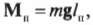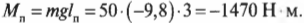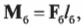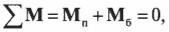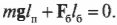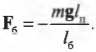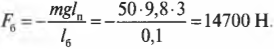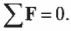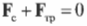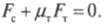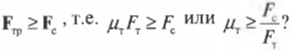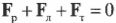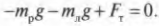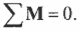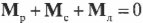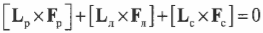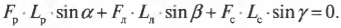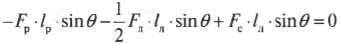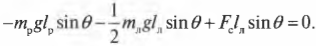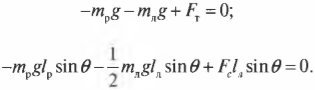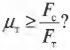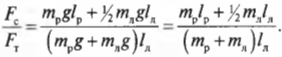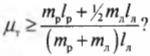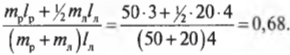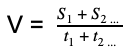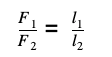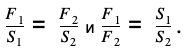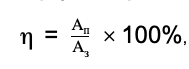|
Есть снаряд 5 грамм, к нему приложили силу в 1.5Н можно ли узнать его скорость какими-то методами? Если да, то какие еще параметры должны быть известны? Давайте представим, что эти параметры у нас есть. По какой формуле тогда будет высчитываться скорость движения данного тела? бонус за лучший ответ (выдан): 5 кредитов Никак без дополнительных параметров. Сила является причиной ускорения по второму занону Ньютона a=F/m. Но скорость в каждый момент времени находится по формуле v=v0+a*t. Поэтому, чтобы узнать скорость, требуется ещё знать её начальное значение и сколько времени с этого момента прошло. Но если речь идёт именно о снаряде, то всё многкратно усложняется. Сила приложена к снаряду только до момента вылета снаряда из ствола и к тому же непостоянна. Сама сила изменяется пропорционально давлению пороховых газов. Кривая давления представлена на рисунке Расчёт скорости и давления ведётся уже по баллистическим формулам, например таким: V=(al)/(b+l); v0=(aL)/(b+L); a=(v0(b+L))/L; P=((φmba^2)/S)*(l/(b+l)^3, где l — путь в стволе, L — длина нарезной части, a,b,φ — пороховые константы, S — площадь поперечного сечения ствола. Но даже в рогатке возникающая сила не постоянная, а обратно пропорциональна натяжению резины, и начальная скорость будет зависеть от этой переменной силы, массы и времени выстрела. Поэтому по тем данным (только сила и масса) практически ничего не вычислишь. система выбрала этот ответ лучшим Kuzmich291192 6 лет назад В данном случае необходимо применить 2 закон Ньютона, но не в привычной для нас форме, а в дифференциальной: F=(p2-p1)/t, где F — сила, приложенная к телу, p1 — импульс тела до приложения силы, p2 — импульс тела после приложения силы, t — время приложения силы. То есть, результирующее значение силы, приложенное к телу есть изменение импульса этого тела за единицу времени. Именно в таком виде Ньютон вывел свой закон. Применим данную формулу. Дано: m=5*10^(-3) кг F=1.5 H Найти: v-? Как я понимаю, начальная скорость снаряда равна 0, следовательно второй закон Ньютона примет вид: F*t=p Расписав импульс и выразив скорость, имеем: F*t=m*v v=F*t/m Из полученной формулы видно, что для нахождения скорости нам необходимо знать время. Действительно, чем больше времени сила будет прилагаться к телу, тем больше она тело разгонит (или же затормозит, если направление силы и направление скорости разнонаправленны). Предположим, что t=1 с. Тогда v=1.5*1/5*10^(-3) v=1500/5 v=300 (м/с). Таким образом, для нахождения скорости тела, в данном случае, мы должны знать силу, действующую на тело, массу тела, и время действия силы на тело (при условии, что тело находилось в состоянии покоя). SVFE48 4 месяца назад Можно рассчитать скорость снаряда, используя силу и массу снаряда, но необходима дополнительная информация. Формула для расчета скорости: Скорость = сила/масса В этом случае сила равна 1,5 Н, а масса равна 5 граммам. Чтобы использовать эту формулу, массу необходимо перевести в килограммы. 1 грамм = 0,001 килограмма 5 грамм = 5 * 0,001 = 0,005 килограмма Таким образом, скорость снаряда можно рассчитать как: Скорость = 1,5 Н / 0,005 кг = 300 м/с Важно отметить, что этот расчет дает только начальную скорость снаряда в момент приложения силы. Чтобы рассчитать конечную скорость, необходимо учитывать другие факторы, такие как сопротивление воздуха, гравитация и угол запуска. Для точного расчета конечной скорости снаряда необходимо знать следующие параметры: угол запуска начальная скорость масса снаряда сопротивление воздуха гравитационное ускорение время полета Когда эти параметры известны, уравнения движения можно использовать для расчета конечной скорости. Стоит отметить, что это упрощенный пример, и в реальных сценариях сопротивление воздуха и угол запуска являются критическими факторами, влияющими на конечную скорость снаряда. dmitriy861 6 лет назад Пусть меня кто то поправит если ошибаюсь, но по моему тут второй закон Ньютона. В общем виде это частное от силы разделённой на массу! Rafail 6 лет назад Если к телу массой 5 г приложить (и не убирать) силу в 1,5 Н, то она, согласно второму закону Ньютона, придаст ему ускорение а=F/m=1,5/0,005=300 м/c^2. Под действием этого ускорения тело начнёт увеличивать скорость по закону v=a*t, где t — время действия силы. Так что, зная формулу Вы можете рассчитать скорость тела в любой момент времени. Михаил Белодедов 6 лет назад Через секунду — 1,5/0,005 = 300 м/с. Через 2 секунды — 600 м/с. Через 3 секунды — 900 м/с. Через 4 секунды — 1,2 км/с. Через 5 секунд — 1,5 км/с. Через 10 секунд — 3 км/с. Через 20 секунд — 6 км/с. А через полминуты скорость достигнет 8 км/с и, если снаряд к тому времени не воткнётся в Землю, он начнёт удаляться от поверхности Земли. Если рассматривать данный вопрос с точки зрения школьных знания то F=m*a , F — сила, m — масса, a — ускорение. Что бы найти скорость в какой либо момент времени, достаточно ускорение умножить на время. Если же учитывать, что есть сила трения, то что сила прилагалась не равномерно и не постоянно, то тут нужны дополнительные данные. Чосик более года назад Мы знаем, что сила равна произведению массы объекта на ускорение. Мы знаем приложенную силу и массу объекта. F= 1.5Н m = 5 = 0.005 кг F = m*a a = F/m a = 1.5/0.005 = 300 м/с. Теперь необходимо связать скорость и ускорение. v=v0+a*t То есть, чтобы узнать скорость движения в определенный момент, необходимо знать время. владсандрович более года назад Скорость эта такая величина, которая в физике обозначается буковкой «V». Если же вы хотите ее найти, то нужно использовать правильную формулу и этой правильной формулой в конечном итоге является v = Ft/m. Буква F в ней обозначает силу, а t — время, а что касается буквы m, то она массу. Aleksandr6052 6 лет назад Скорость можно определить по формуле: v = Ft/m. Здесь v — скорость, F — сила, t — время, m — масса. То есть, чтобы успешно решить поставленную задачку нам недостаёт ещё одной физической величины, а именно — времени. Знаете ответ? |
В статье обсуждаются несколько подходов к вычислению скорости по силе и массе, а также решенные проблемы.
Чтобы вычислить скорость, мы должны понять, насколько далеко уходит масса объекта при приложении силы. Скорость объекта — это не что иное, как величина его вектора скорости. Вот почему мы можем рассчитать скорость по силе и массе, используя законы Ньютона, кинематическое уравнение движения и формулы работы-энергии.
Подробнее о том, как рассчитать массу по силе и расстоянию.
Как рассчитать скорость по силе и массе, используя второй закон Ньютона?
Давайте вычислим скорость по силе и массе, используя второй закон движения Ньютона.
Второй закон Ньютона связывает скорость изменения скорости или ускорение с приложенной силой и массой. Вычислять скорость из второго закона Ньютона, нам сначала нужно понять разницу между скоростью и скоростью, а затем вычислить значение скорости из скорости изменения скорости.
Согласно Второй закон Ньютона,
F = ma
]
F=m*[(vv0)/(тт0)
В то время как v0 — начальная скорость, v — конечная скорость.
Прежде чем рассчитывать скорость по закону Ньютона, давайте разберемся в разнице между скоростью и скоростью.
от силы и массы
Разница между скоростью и скоростью
| Скорость | Скорость |
| Это скалярная величина, связанная с расстоянием. | Это векторная величина, связанная со смещением. |
| Это ненулевая величина, которая всегда положительна. | Может быть нулевым, положительным и отрицательным. |
| Это может не быть равным скорости. | Разные скорости одного и того же объекта обладают одинаковой скоростью. |
| Единица СИ — метр в секунду (м / сек). | Единица СИ — километр / час (км / час). |
(Кредит: Shutterstock)
Когда автомобиль проехал определенное расстояние d за время t, мы называем его скорость v.
v=d/t
Как вы знаете, иногда нам нужно изменить направление во время движения из-за пробок или по другим причинам; в этом случае мы измеряем смещение вместо расстояния d в интервале времени t.
Уравнение (*) превращается в скорость v как,
Смещение — это кратчайшее расстояние между конечным и начальным расстоянием, но его величина меньше или равна общему расстоянию d.
(Кредит: Shutterstock)
Поскольку скорость не равна нулю или никогда не уменьшается со временем, величина скорости становится значением скорости, когда время приближается к нулю.
Это означает скорость v говорит нам, насколько быстро машина. В то время как скорость v говорит нам как о скорости автомобиля, так и о его направлении. Поэтому мы назвали скорость величиной вектора скорости.
Узнать больше об относительном движении.
Автомобиль массой 1000 кг в состоянии покоя проехал около 1 часа при силе 6 х 104 Применяется N. Рассчитайте скорость автомобиля.
Данный:
F = 6 х 104 N
m = 1000 кг
t = 1 час
Найти: v=?
Формула:
F = ma
Решение:
Скорость автомобиля рассчитывается с использованием Второй закон движения Ньютона.
F = ма
F=m*[(vv0)/(тт0)
Поскольку автомобиль изначально находится в состоянии покоя, v0 = 0 и t0 = 0
Следовательно,
Подставляя все значения,
Преобразуем скорость в скорость в метрах в секунду.
1 км = 1000 м
1 час = 3600 секунд
v=60*(1000/3600)
v = 60000/3600
v = 16.6
Автомобиль движется со скоростью 16.6 м / сек.
Подробнее о том, как рассчитать ускорение свободного падения.
Как рассчитать скорость по силе и массе, используя кинематическое уравнение движения?
Давайте вычислим скорость по силе и массе, используя второе кинематическое уравнение движения.
Второе кинематическое уравнение движения связывает общее пройденное расстояние объекта с начальной скоростью и ускорением. Когда мы внедрили формулу ускорения из второго закона Ньютона в кинематическое уравнение, мы получили формулу, которая рассчитывала скорость на основе приложенной силы и ее массы.
Второе кинематическое уравнение движения:
Узнать больше о кинематических уравнениях движения.
Парашютист массой 60 кг выпрыгивает из самолета и за 1 минуту достигает земли. Если сила, воздействующая на парашютиста по воздуху, составляет 800 Н, какова скорость парашютиста?
Данный:
m = 60 кг
t = 1 минута = 60 секунд
F = 800 Н
Найти: v =?
Формула:
Решения:
Скорость парашютиста рассчитывается с помощью второе кинематическое уравнение движения.
а=Ф/м
Но
Поскольку парашютист изначально находится в состоянии покоя относительно плоскости, следовательно, d0 = 0 и v0 = 0.
d=(1/2)*(Ф/м)*t2
С скорость v= d / t
vt=(1/2)*(Ф/м)*t2
v=фут/2м
Подставляем все значения
v=(800*60)/(2*60)
v = 48000/120
V = 400
Скорость парашютиста 400 м / сек.
Подробнее о преобразовании потенциала в кинетическую энергию.
Как рассчитать скорость по силе и массе, используя формулу работы-энергии?
Давайте вычислим скорость по силе и массе, используя формулу работы-энергии.
Когда покоящийся объект перемещается на определенное расстояние при приложении силы, он выполняет работу. Приложенная сила преобразует накопленную потенциальную энергию неподвижного объекта в кинетическую энергию для выполнения работы. Вот почему используется формула работы-энергии; мы можем вычислить скорость по силе и массе.
Компания формула работы является,
W = Fd
Поскольку работа, совершаемая телом, есть приобретение им кинетической энергии KE=(1/2)mv2
(1/2)мв2 =Fд
Узнать больше о выполненной работе.
Мужчина имеет горки массой 80 кг со скоростью 30 км / ч за 2 секунды, когда к нему прилагается сила 200 Н, когда он толкает горку на игровой площадке. Рассчитайте скорость скольжения человека.
Данный:
F = 200 Н
m = 80 кг
v=30км/ч=30*(1000/3600)
t = 2 часа
Найти: v=?
Формула:
(1/2)мв2=Fд
Решения:
Скорость скольжения человека рассчитывается с помощью формула работы-энергии в виде,
(1/2)мв2=Fд
Но скорость v = d / t
(1/2)мв2=Fdt
v=мв2/2 фута
Используя формулу работы и энергии, мы можем вычислить скорость в терминах силы, массы и скорости.
Подставляя все значения,
v=(72*106)/(28.8*105)
v = 25
Скорость скольжения человека 25 м / сек.
Узнайте больше о проделанной работе на уклоне.
Как рассчитать скорость по силе и массе с помощью формулы мощности?
Давайте рассчитаем скорость по силе и массе, используя формулу мощности.
Мощность любого объекта измеряется количеством его работы, выполненной за единицу времени. Поскольку проделанная работа объекта является произведением приложенной силы и пройденного расстояния. Следовательно, используя формулу мощности, мы можем рассчитать скорость объекта непосредственно из приложенной силы и ее мощности.
Компания формула мощности является,
P=Вт/т
W = Fd
Но работа сделана
P=Fd/т
v=d/t
Поскольку скорость
Р=Fv
(Кредит: Shutterstock)
Узнать больше о Power.
Если номинальная мощность двигателя составляет 500 Вт, он может выполнять работу при приложении силы 80 Н. Какая скорость у мотора?
Данный:
P = 500 Вт
1Вт=1кг.м2/s3
F = 80 Н
1Н=1кг.м2/s2
Найти: v=?
Формула:
P=Вт/т
Решения:
Скорость рассчитывается с использованием формула мощности,
P = Fv
v=П/Ф
Подставляя все значения,
В=500Вт/80Н
v = 40 м / сек
Скорость двигателя 40 м / сек.
В этой главе…
- Переходим от поступательного движения к вращательному движению
- Вычисляем тангенциальную скорость и тангенциальное ускорение
- Выясняем связь между угловым ускорением и угловой скоростью
- Разбираемся с моментом силы
- Поддерживаем вращательное движение
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!
Содержание
- Переходим от прямолинейного движения к вращательному
- Разбираемся с параметрами вращательного движения
- Вычисляем линейную скорость вращательного движения
- Вычисляем тангенциальное ускорение
- Вычисляем центростремительное ускорение
- Используем векторы для изучения вращательного движения
- Определяем направление угловой скорости
- Определяем направление углового ускорения
- Поднимаем грузы: момент силы
- Знакомимся с формулой момента силы
- Разбираемся с направлением приложенной силы и плечом силы
- Размышляем над тем, как создается момент силы
- Определяем направление момента силы
- Уравновешиваем моменты сил
- Простой пример: вешаем рекламный плакат
- Более сложный пример: учитываем силу трения при расчете равновесия
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- ( v=Delta{s}/Delta{t} ), где ( v ) — это скорость, ( Delta{s} ) — перемещение, a ( Delta{t} ) — время перемещения;
- ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
- ( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени;
- ( v^2_1-v^2_0=2aDelta{s} ), где ( v_1 ) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta{theta}/Delta{t} ), где ( omega ) — угловая скорость, ( Delta{theta} ) — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
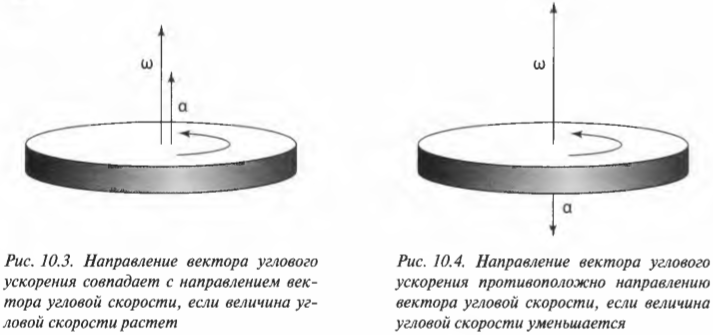
- ( alpha=Delta{omega}/Delta{t} ), где ( alpha ) — угловое ускорение, ( Delta{omega} ) — изменение угловой скорости, ( Delta{t} ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ), где ( omega_1 ) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
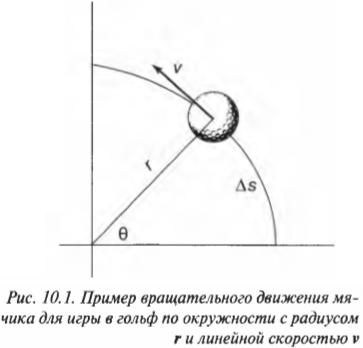
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf{r} ) и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).
Угловая скорость связана с линейной скоростью соотношением ( v=romega ), которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ), а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ), охватывающая угол ( Deltatheta ), равна:
Из формулы прямолинейного движения
путем подстановки выражения для ( Delta s ) получим:
Поскольку:
где ( omega ) — угловая скорость, ( Delta{theta} )— угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} ), то:
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:
Подставляя в нее значения, получим:
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
Подставим это выражение в предыдущую формулу линейного ускорения:
Поскольку радиус остается постоянным, то его можно вынести за скобки:
Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ), то:
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ), получим:
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
После подстановки этого значения в предыдущую формулу получим:
Средний радиус орбиты Луны равен 3,85·108 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Зная это ускорение и массу Луны, которая равна 7,35·1022 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
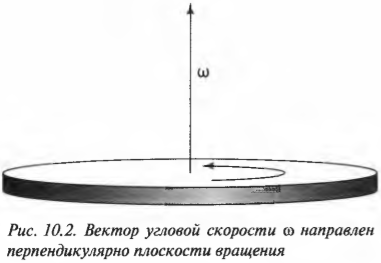
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t )— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где ( mathbf{alpha} ) — вектор углового ускорения, а ( Deltamathbf{omega} ) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
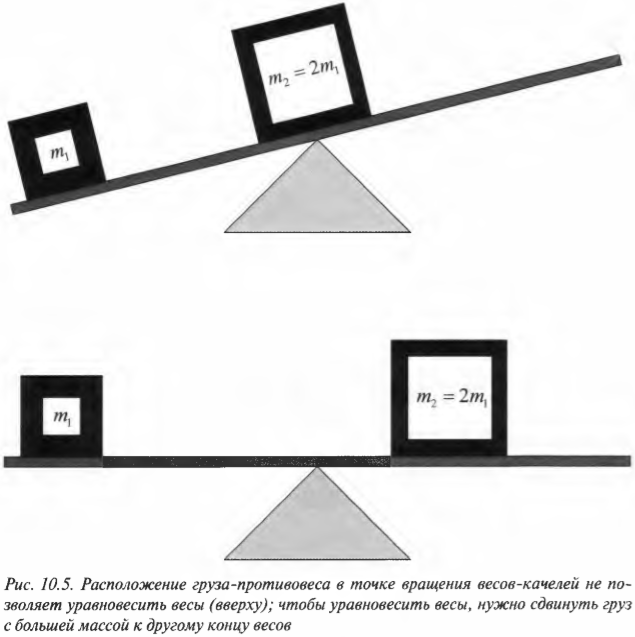
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ).
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
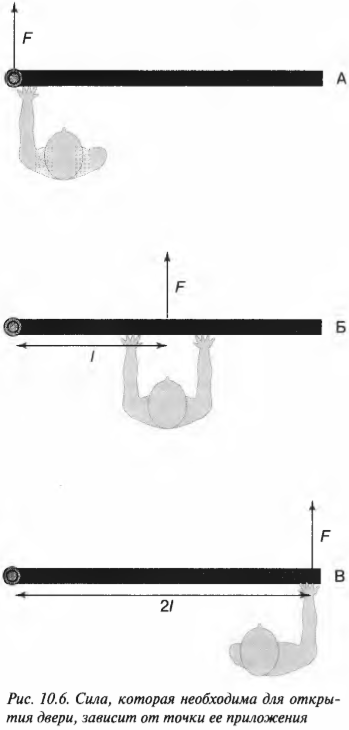
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ):
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
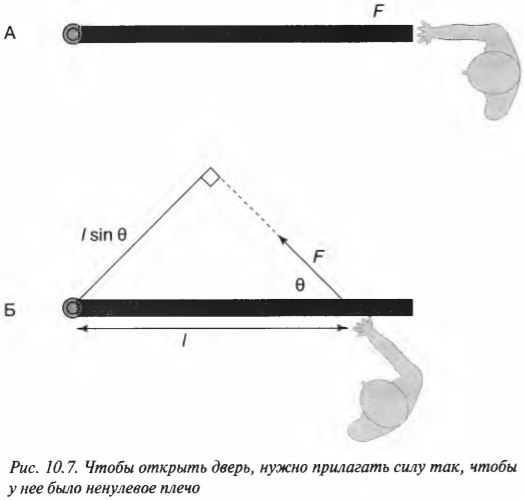
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ). Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
Однако в данном случае угол ( theta ) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
Определяем направление момента силы
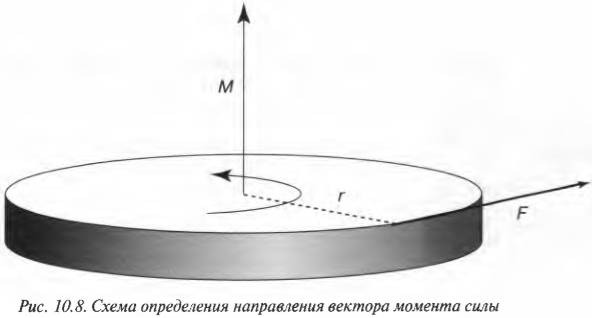
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
На рис. 10.8 показан пример силы ( mathbf{F} ) с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.
Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
Иначе говоря:
где ( mathbf{M_п} ) — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
где ( m ) = 50 кг — это масса плаката, ( mathbf{g} ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf{g} ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
получим, что:
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
Более сложный пример: учитываем силу трения при расчете равновесия
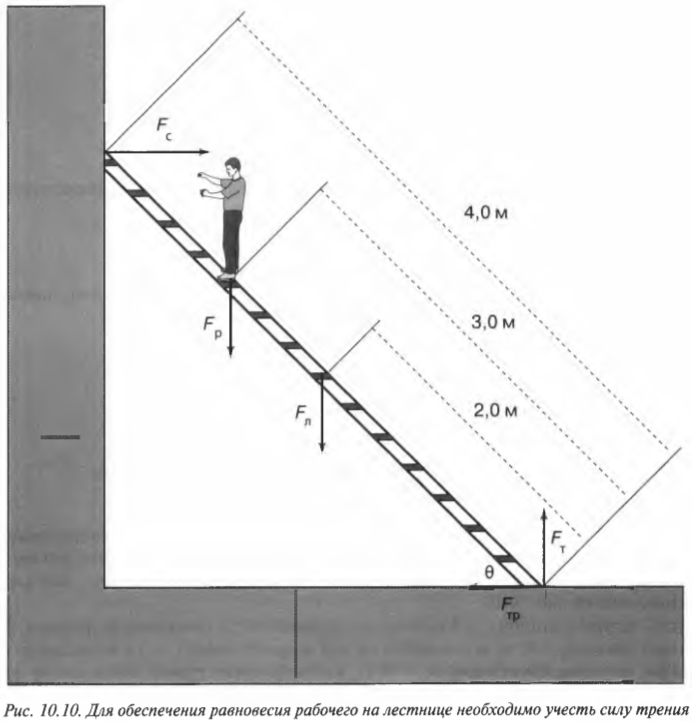
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- ( mathbf{F_с} ) — нормальная сила со стороны стены;
- ( mathbf{F_р} ) — вес рабочего;
- ( mathbf{F_л} ) — вес лестницы;
- ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
- ( mathbf{F_т} ) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:
или
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:
или
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf{M_р=[L_р!times! F_р]} ), весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):
или
или
Поскольку ( L_р=l_р ), ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ( alpha=360^{circ}-theta ), ( beta=360^{circ}-theta ) и ( gamma=theta ), то получим:
или
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):
Зададимся вопросом: соблюдается ли условие
Из системы двух уравнений получим:
Итак, остается выяснить, соблюдается ли условие:
После подстановки значений получим:
Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
Глава 10. Вращаем объекты: момент силы
3.4 (68.5%) 40 votes
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Сила скорости представляет физическую величину, характеризуемую отношением перемещения к промежутку времени, за которое и произошло оное перемещение.
Понятие силы скорости
Замечание 1
Сила скорости представляет одну из главных характеристик механического движения.
Она является выражением самой сути движения, определяя то отличие, которое присутствует между телом в неподвижном и подвижном состояниях.
В системе измерений общепринятого формата скорость измеряется в метрах за секунду. Иными словами, в физике в качестве единицы скорости обозначена скорость определенного равномерного прямолинейного движения, за одну секунду при котором телом будет совершен путь в один метр. В качестве единицы измерения скорости зачастую выступает вышеуказанный формат, однако частые случаи измерения скорости и в других единицах. Чтобы измерить скорость транспортных средств, например, обычно применяют единицу измерения, которая характеризуется пройденными за час километрами.
Важно знать, что скорость представляет векторную величину. Направление вектора скорости определяют, согласно определенной траектории движения. Вектор скорости при этом будет всегда направленным по касательной к траектории в точке прохождения движущегося объекта передвижения.
Пример 1
В качестве примера можно рассмотреть колесо едущего автомобиля. Колесо в момент движения будет вращаться, а все его точки при этом движутся по окружности. Брызги, которые от него разлетаются, также будут лететь по касательным к данным окружностям, указывая таким образом направления векторов скоростей отдельно взятых точек колеса.
Сила скорости, таким образом, может считаться характеристикой направления движения тела (направления вектора скорости) и быстроты его перемещений (модуль вектора скорости). При этом скорость тела может оказаться и отрицательной. Это будет означать движение тела в том направлении, которое считается противоположным направлению оси координат в избранной системе отсчета.
«Сила скорости, формулы» 👇
Виды скорости
Сила скорости будет зависеть от времени. Согласно характеру зависимости ее от времени, движение существует в таком виде:
- равномерное (движение с постоянной по модулю скоростью);
- неравномерное (в этом случае имеет место так называемая «средняя скорость»).
Средняя скорость определяется на основании такой формулы:
$vec{U_ср} = frac{vec{delta s}}{delta t}$
Мгновенная скорость представляет показатель скорости в конкретный момент времени, являясь физической величиной, равной пределу, к которому будет стремиться средняя скорость в условиях бесконечного сокращения промежутка времени $delta t$:
$vec{U} = Lim_{delta tto 0}frac{vec{delta s}}{delta t}$
Мгновенная скорость, таким образом, в конкретный момент времени будет считаться соотношением очень незначительного перемещения $vec{delta s}$ к очень малому временному промежутку, за который и осуществлялось данное перемещение. Вектор мгновенной скорости направляется по касательной к траектории передвижения тела
Закон сложения скоростей на примерах
В разных системах отсчета силы скоростей движения тела будет связывать между собой классический закон сложения скоростей, который звучит таким образом: скорость тел относительно неподвижной системы отсчета равнозначна сумме скоростей в подвижной системе и наиболее подвижной системы отсчета в отношении к неподвижной.
На примерах можно рассмотреть движение пассажирского поезда по железной дороге при скорости 65 км/ч. По вагону такого поезда человек может перемещаться со скоростью, например, в 5 км/ч. Если воспринимать что железная дорога неподвижная и принимать ее за систему отсчета, тогда скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скорости поезда и человека.
В первом случае скорость определяется сложением, поскольку человек перемещается в одном направлении с поездом, то есть скорость будет 70 км/ч (65 + 5).
Что касается второго случая, то он имеет место в ситуации, когда поезд и человек движутся в разных направлениях, то есть скорость получится 60 км/ч (65 – 5).
Однако это будет справедливым только в случае передвижения человека и поезда по одной линии. Если же имеет место перемещение человека под некоторым углом, тогда нужно будет учитывать и этот угол, понимая, что скорость является все-таки векторной величиной.
Вышеприведенный пример стоит рассмотреть более подробно для лучшего понимания действия силы скорости. Железная дорога в данном случае представляет неподвижную систему отсчета. В то же время, поезд, который по ней движется, будет подвижной системой. Вагон, по которому движется человек, представляет часть поезда.
Замечание 2
Относительно вагона скорость человека будет равной пяти километрам в час и характеризоваться такой величиной, как $vec{delta U_ч}$. Скорость поезда (и, соответственно, вагона) относительно неподвижной системы будет равной 65 км/ч, обозначим ее как $vec{delta U_в}$.
За незначительный промежуток времени $delta t$ успеют произойти такие события:
Человек будет перемещаться относительно вагона на расстояние $vec{delta S_ч}$;
Относительно железной дороги вагон будет перемещаться на такое расстояние: $vec{delta S_в}$.
В таком случае, за данный временной промежуток относительно железной дороги перемещение человека определяется таким образом:
$vec{delta S} = vec{delta S_ч}+vec{delta S_в}$
Это называется законом сложения перемещений. В приведенном примере перемещение человека относительно железной дороги будет равнозначно сумме его перемещений относительно вагона и также вагона относительно самой железной дороги:
$vec{delta S = vec{delta U_ч}delta t+vec{delta U_в}delta t}$
Скорость человека относительно железной дороги тогда будет равной:
$vec{U} = frac{vec{delta S}}{delta t}$
Поскольку $vec{delta S} = vec{delta S_ч}+vec{delta S_в}$, то
$U=frac{vec{delta S}}{delta t}=frac{{vec{delta S_ч}+vec{delta S_в}}{delta t}=frac{vec{delta S_ч}}{delta t}+{delta S_в}}{delta t}$
Скорость человека относительно вагона тогда будет определяться так:
$vec{delta U_ч} = frac{vec{delta S_ч}}{delta t}$
Скорость вагона относительно железной дороги составит:
$vec{delta U_в} = frac{vec{delta S_в}}{delta t}$
Таким образом, сила скорости человека относительно железной дороги определяется следующим образом:
$vec{U} = vec{delta U_ч}+vec{delta U_в}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины.
Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
-
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
-
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
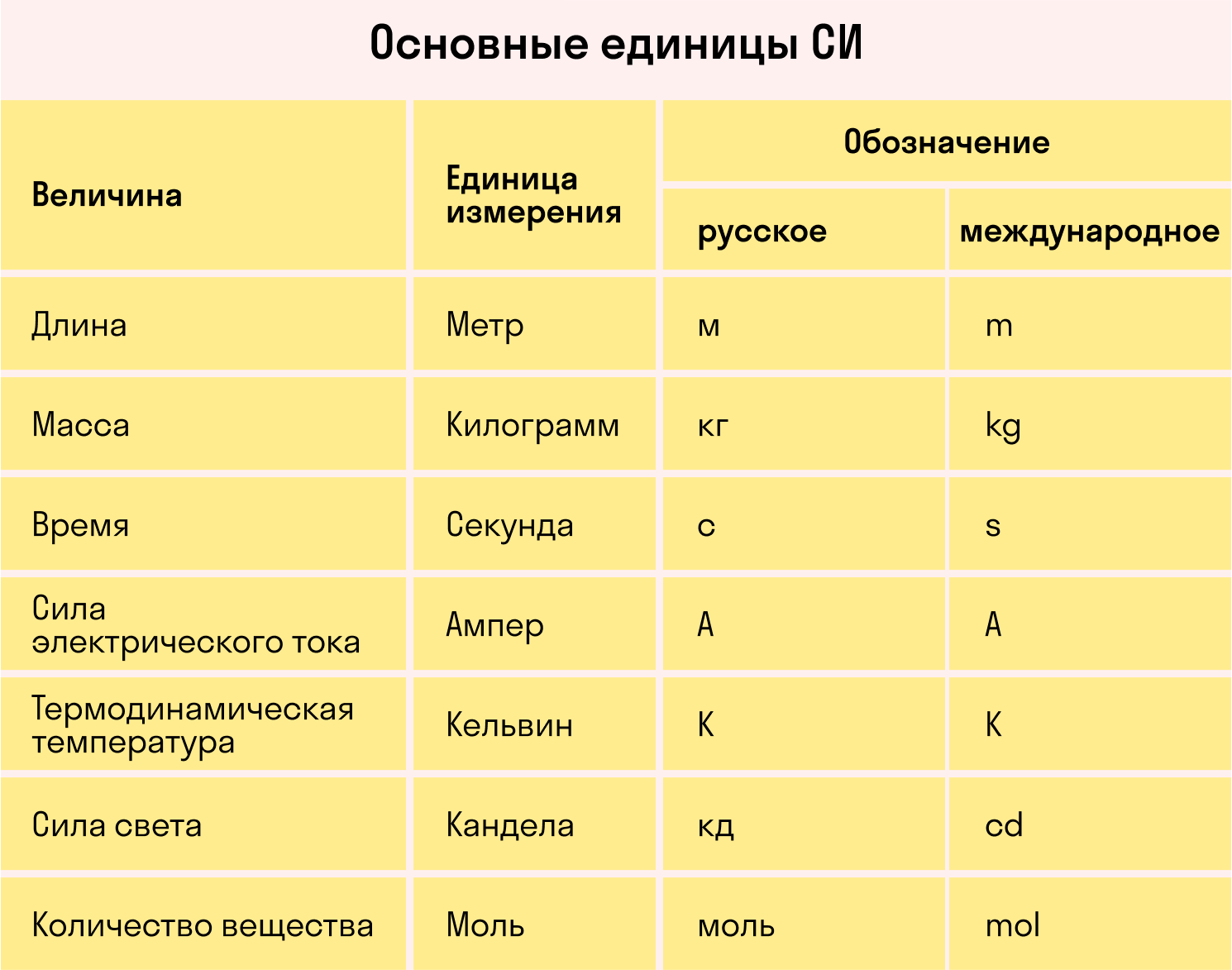
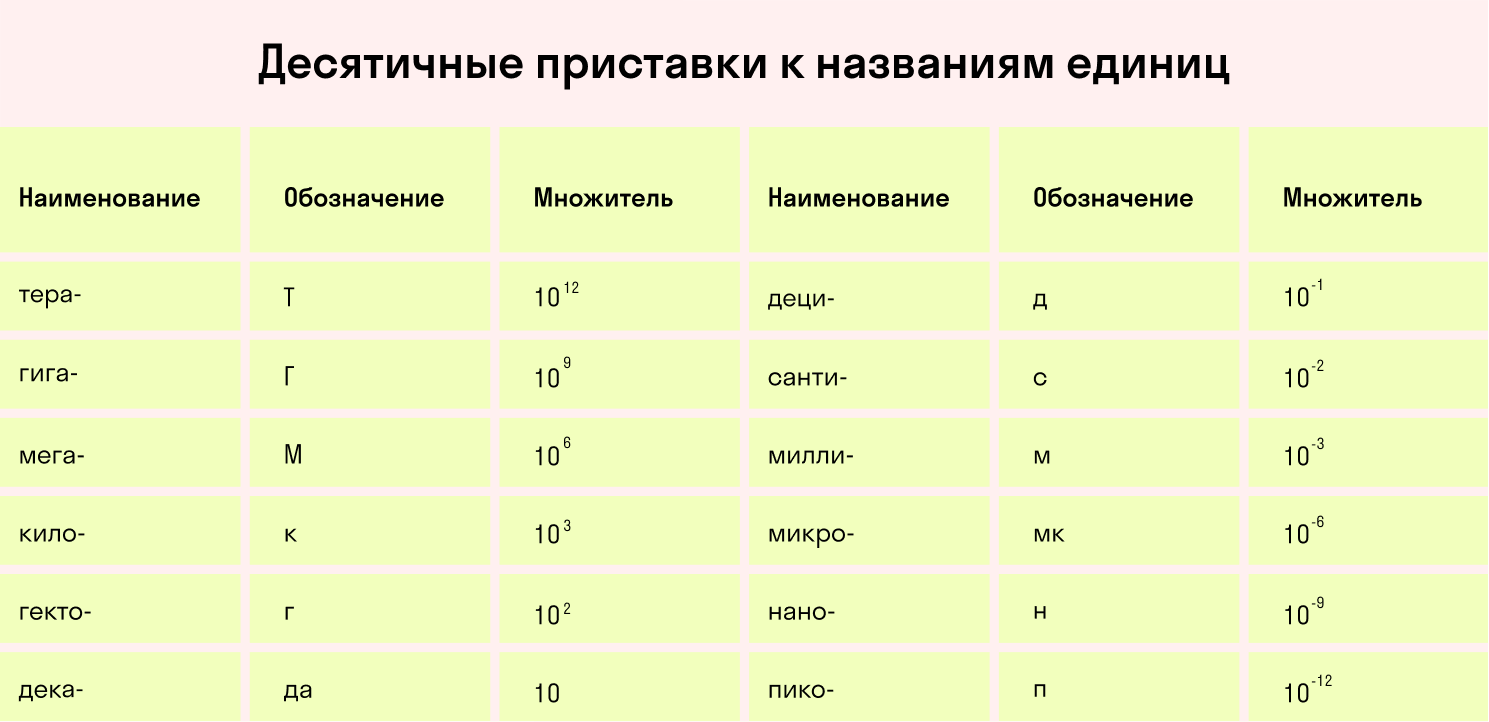
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
-
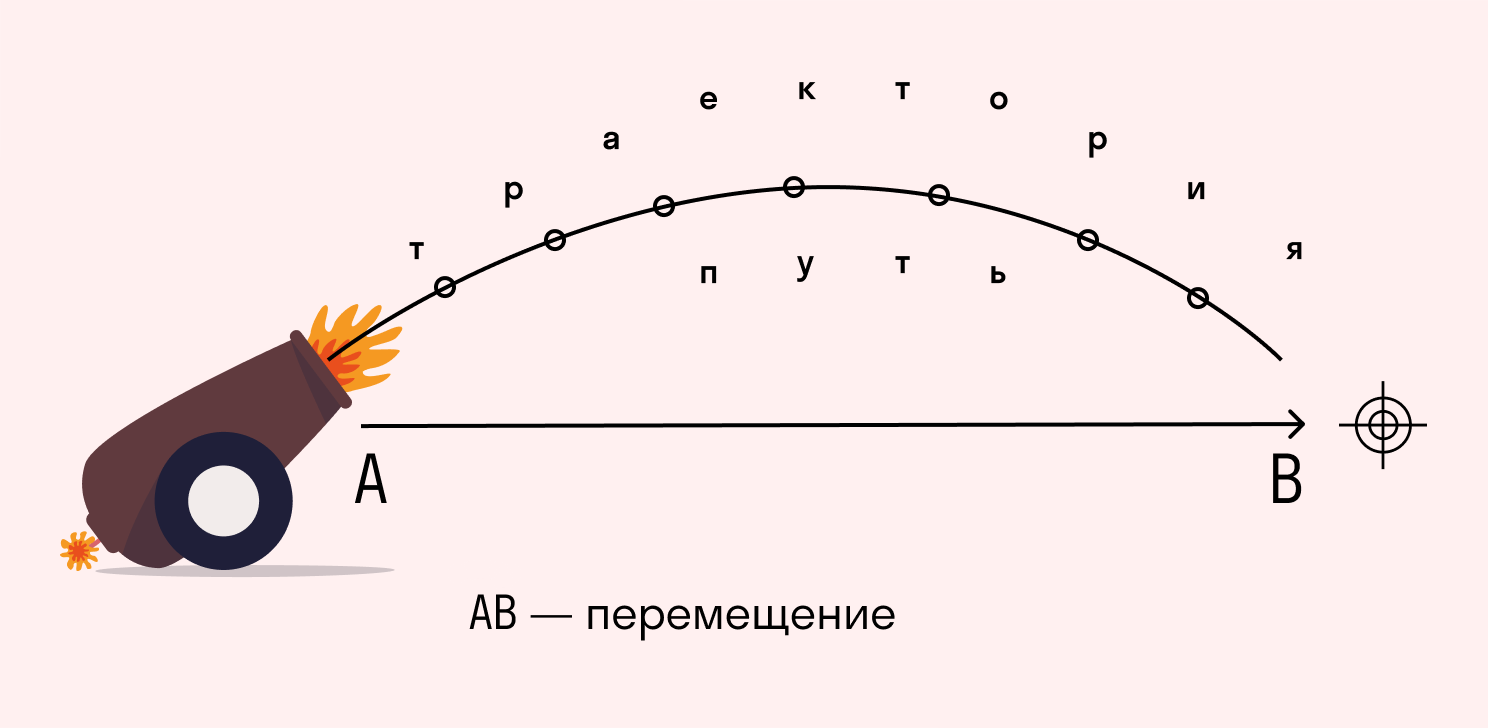
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
-
Траектория движения — мысленная линия, вдоль которой перемещается тело.
-
Путь — длина траектории тела от начальной до конечной точки.
-
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
-
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние.
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
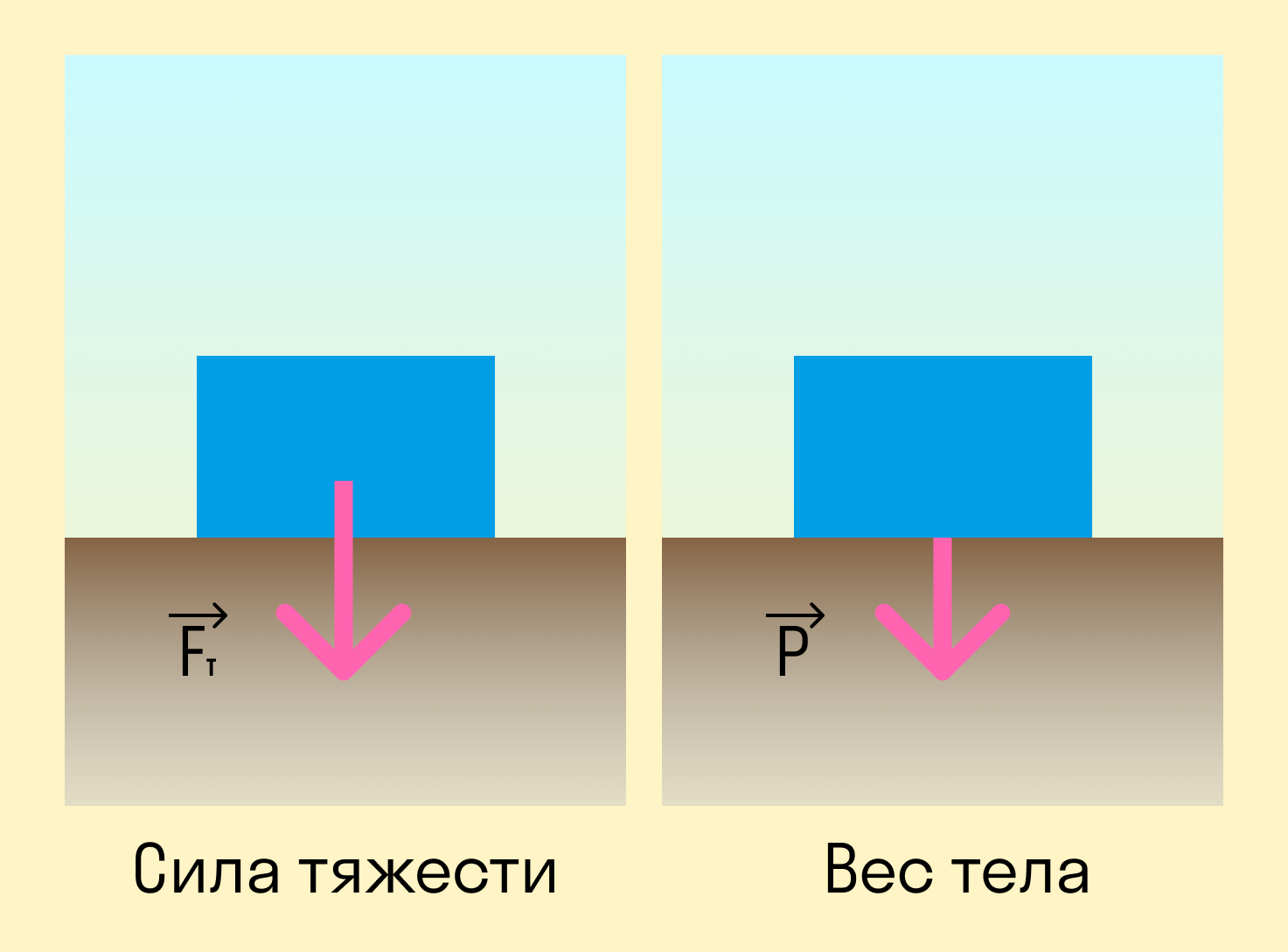
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз.
Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.
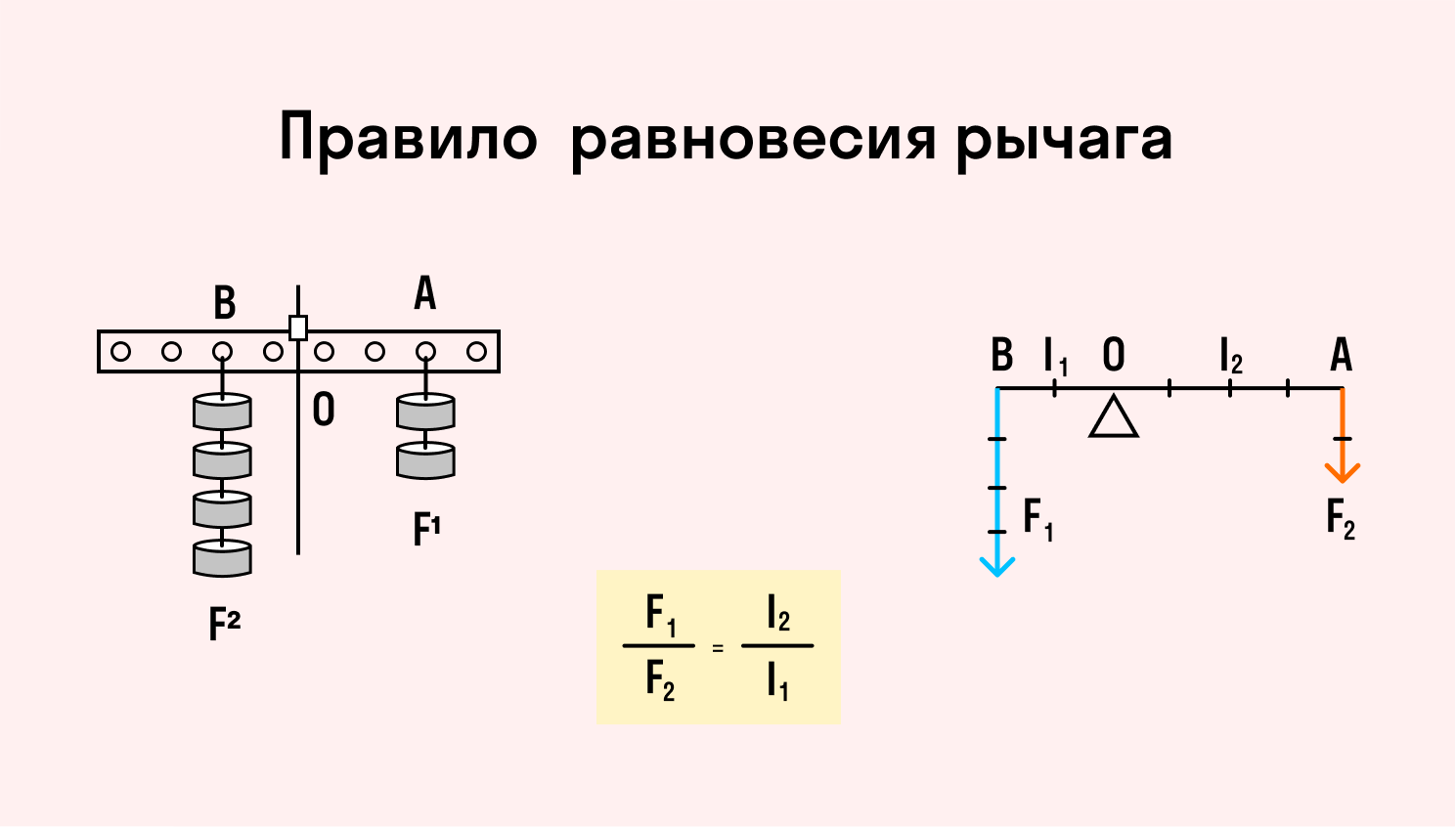
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l.
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
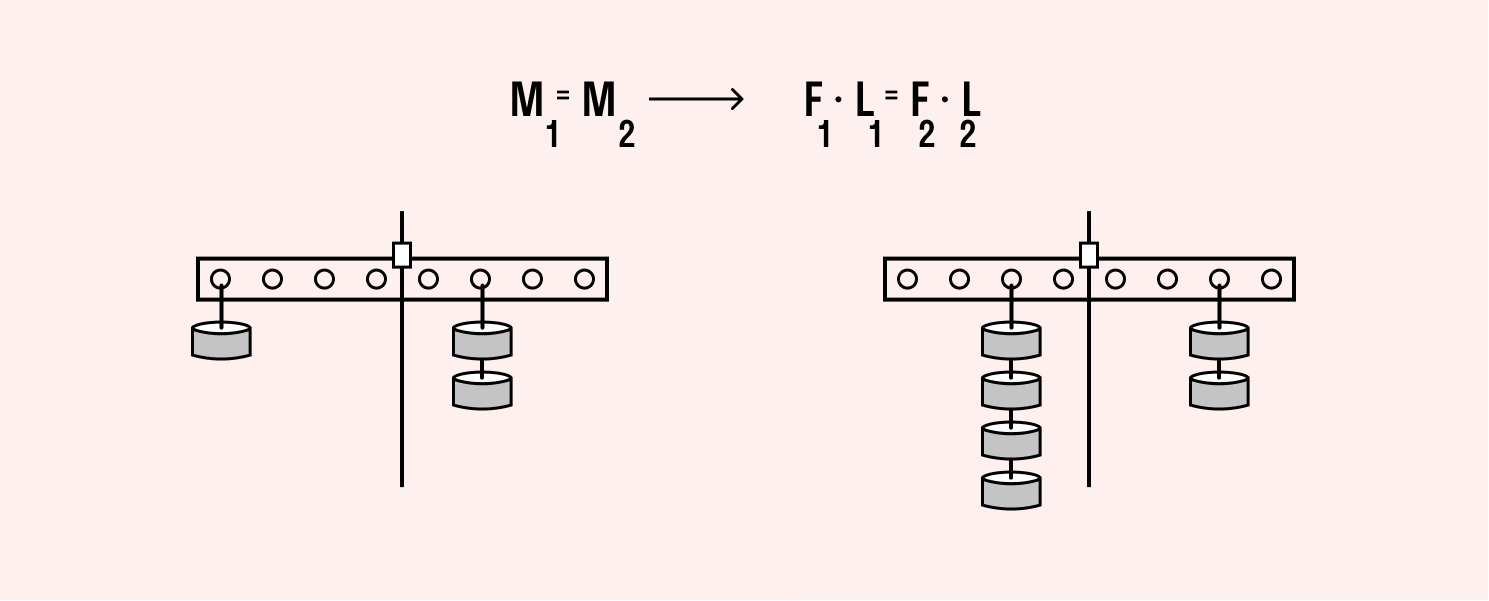
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
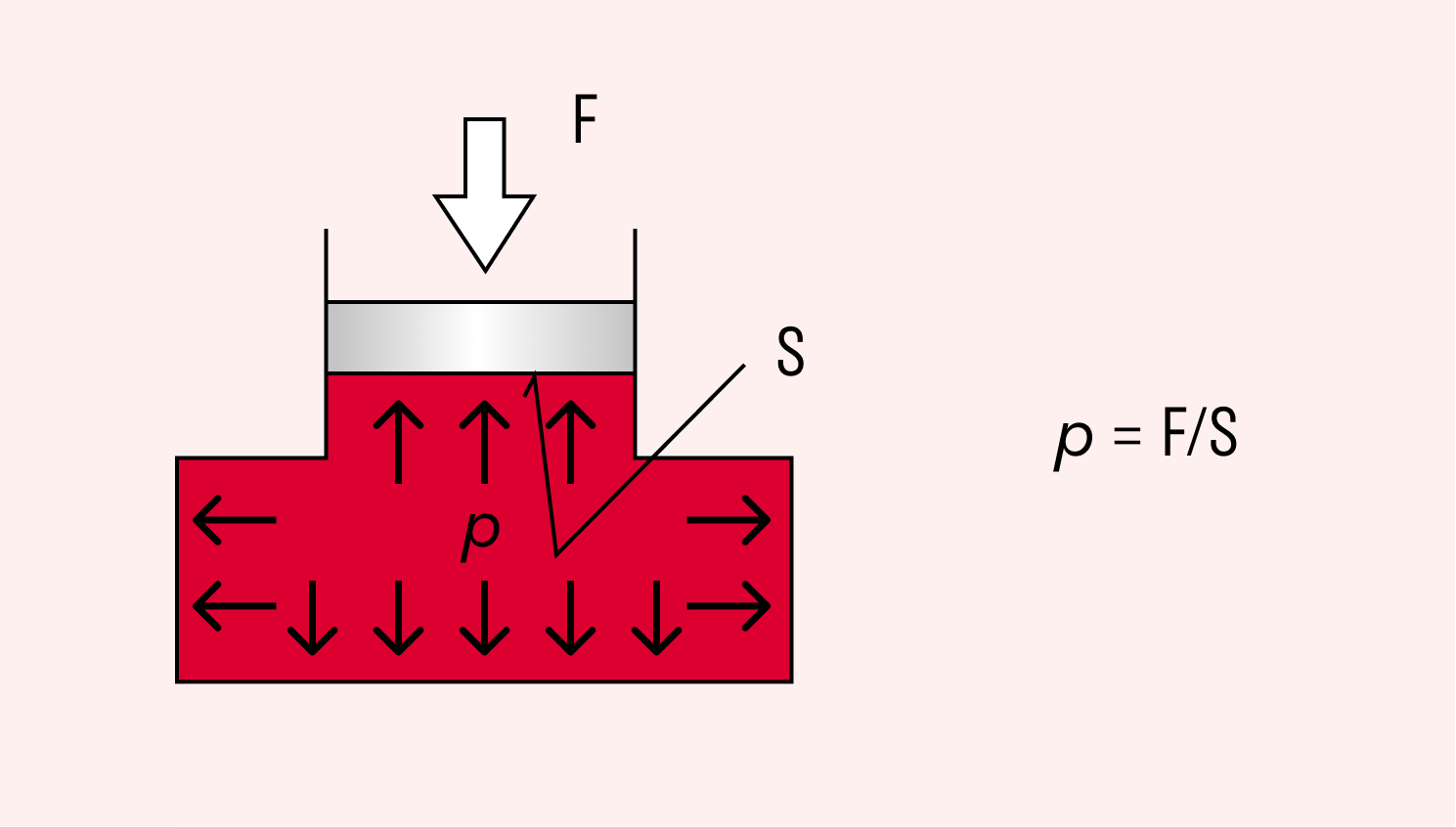
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
Сила давления направлена перпендикулярно поверхности.
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
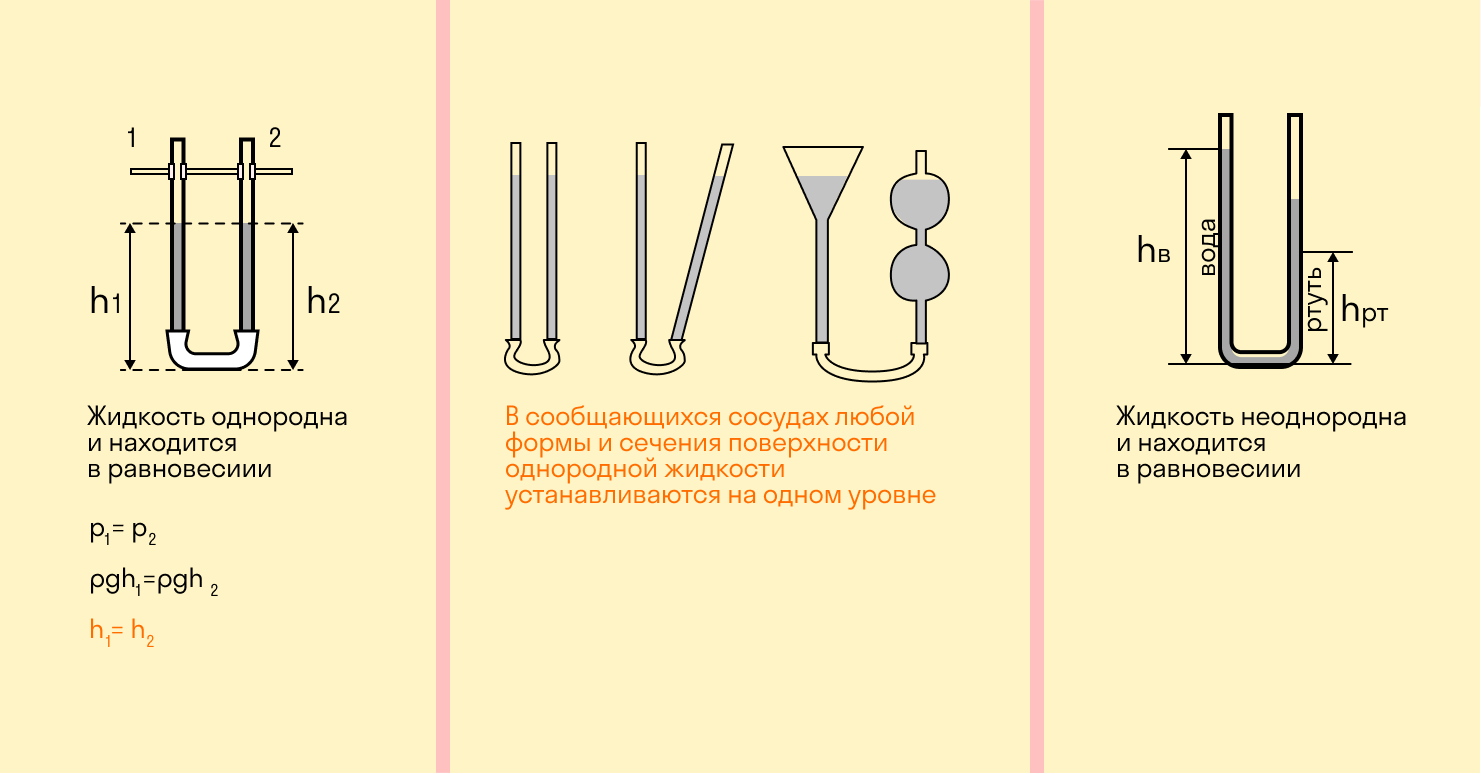
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
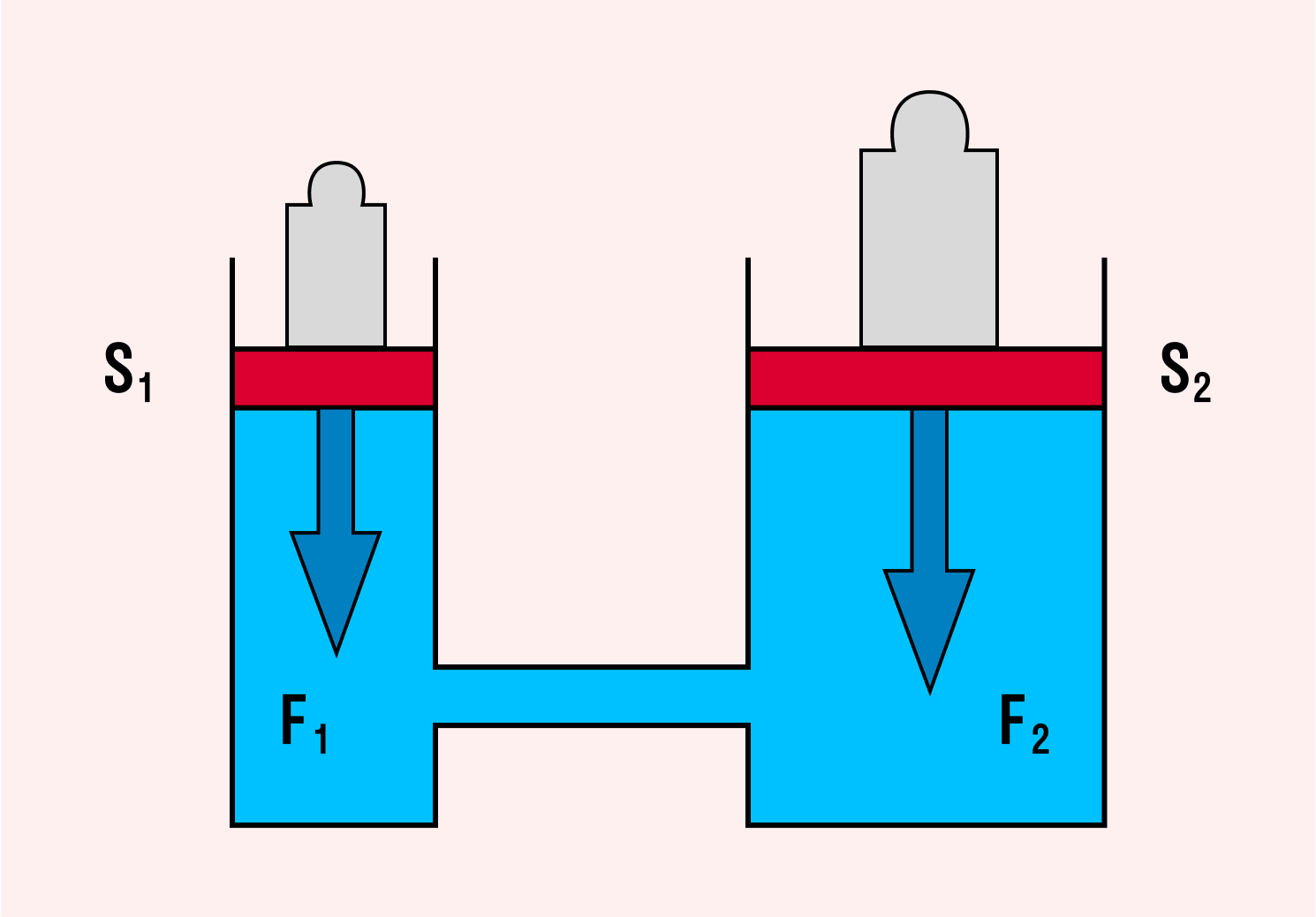
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
-
если плотность тела выше плотности среды, оно уйдет на дно;
-
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение.
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
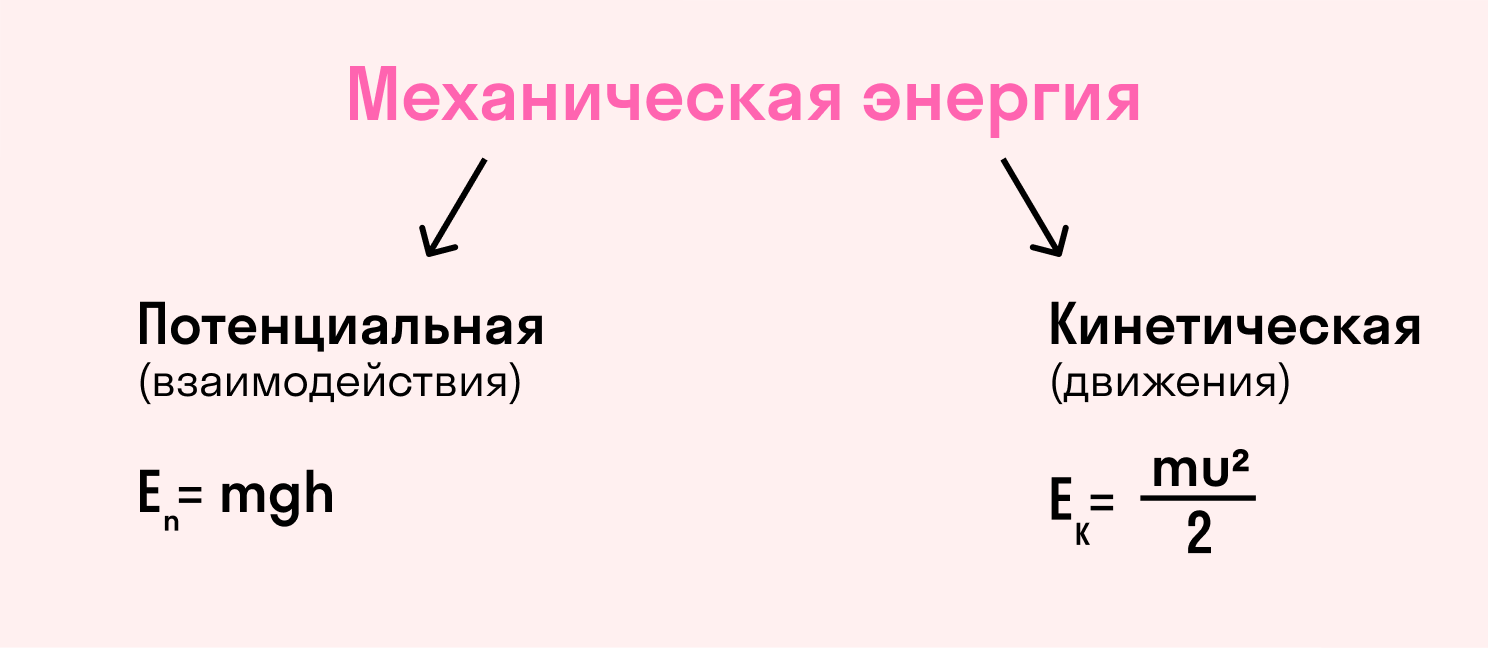
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
-
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
-
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
|
Кинетическая энергия |
Пропорциональна массе тела и квадрату его скорости. |
Ek = mv2/2 |
|
Потенциальная энергия |
Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. |
Ep= mgh |
|
Полная механическая энергия |
Складывается из кинетической и потенциальной энергии. |
E = Ek+Ep |
|
Сохранение и превращение энергии |
Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. |
Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!