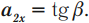Как найти скорость в любой момент времени - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Скорость — это быстрота перемещения объекта в заданном направлении. ^[1] В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела.^[2]

1
Начните с уравнения. Для вычисления мгновенной скорости необходимо знать уравнение, описывающее перемещение тела (его позицию в определенный момент времени),^[3] то есть такое уравнение, на одной стороне которого находится s (перемещение тела), а на другой стороне — члены с переменной t (время).^[4] Например:

s = -1.5t² + 10t + 4
- В этом уравнении:
  
  Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 — 7 = 3 м (а на 10 + 7 = 17 м).
  
  Время = t. Обычно измеряется в секундах.
2
Вычислите производную уравнения. Чтобы найти мгновенную скорость тела, чьи перемещения описываются приведенным выше уравнением, нужно вычислить производную этого уравнения. Производная — это уравнение, позволяющее вычислить наклон графика в любой точке (в любой момент времени). Чтобы найти производную, продифференцируйте функцию следующим образом: если y = a*xⁿ, то производная = a*n*x^n-1. Это правило применяется к каждому члену многочлена.
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
  
  s = -1.5t² + 10t + 4
  (2)-1.5t^(2-1) + (1)10t^{1 — 1} + (0)4t⁰
  -3t¹ + 10t⁰
  -3t + 10
3
Замените «s» на «ds/dt», чтобы показать, что новое уравнение — это производная от исходного уравнения (то есть производная s от t). Производная — это наклон графика в определенной точке (в определенный момент времени). Например, чтобы найти наклон линии, описываемой функцией s = -1.5t² + 10t + 4 при t = 5, просто подставьте 5 в уравнение производной.
- В нашем примере уравнение производной должно выглядеть следующим образом:
  
  ds/dt = -3t + 10
4
В уравнение производной подставьте соответствующее значение t, чтобы найти мгновенную скорость в определенный момент времени.^[5] Например, если вы хотите найти мгновенную скорость при t = 5, просто подставьте 5 (вместо t) в уравнение производной ds/dt = -3 + 10. Затем решите уравнение:

ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 м/с
- Обратите внимание на единицу измерения мгновенной скорости: м/с. Так как нам дано значение перемещения в метрах, а время — в секундах, и скорость равна отношению перемещения ко времени, то единица измерения м/с — правильная.
Реклама

1
Постройте график перемещения тела. В предыдущей главе вы вычисляли мгновенную скорость по формуле (уравнению производной, позволяющему найти наклон графика в определенной точке).^[6] Построив график перемещения тела, вы можете найти его наклон в любой точке, а следовательно определить мгновенную скорость в определенный момент времени.
- По оси Y откладывайте перемещение, а по оси X — время. Координаты точек (x,у) получите через подстановку различных значений t в исходное уравнение перемещение и вычисления соответствующих значений s.
- График может опускаться ниже оси X. Если график перемещения тела опускается ниже оси X, то это значит, что тело движется в обратном направлении от точки начала движения. Как правило, график не распространяется за ось Y (отрицательные значения x) — мы не измеряем скорости объектов, движущихся назад во времени!
2
Выберите на графике (кривой) точку P и близкую к ней точку Q. Чтобы найти наклон графика в точке P, используем понятие предела. Предел — состояние, при котором величина секущей, проведенной через 2 точки P и Q, лежащих на кривой, стремится к нулю.
- Например, рассмотрим точки P(1,3) и Q(4,7) и вычислим мгновенную скорость в точке P.
3

Найдите наклон отрезка PQ. Наклон отрезка PQ равен отношению разницы значений координат «у» точек P и Q к разнице значений координат «х» точек P и Q. Другими словами, H = (y_Q — y_P)/(x_Q — x_P), где H — наклон отрезка PQ. В нашем примере наклон отрезка PQ равен:

H = (y_Q — y_P)/(x_Q — x_P)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33
4

Повторите процесс несколько раз, приближая точку Q к точке P. Чем меньше расстояние между двумя точками, тем ближе значение наклона полученных отрезков к наклону графика в точке P. В нашем примере проделаем вычисления для точки Q с координатами (2,4.8), (1.5,3.95) и (1.25,3.49) (координаты точки P остаются прежними):

Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8

Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9

Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96
5
Чем меньше расстояние между точками P и Q, тем ближе значение H к наклону графика в точке P При предельно малом расстоянии между точками P и Q, значение H будет равно наклону графика в точке P Так как мы не можем измерить или вычислить предельно малое расстояние между двумя точками, графический способ дает оценочное значение наклона графика в точке Р.
- В нашем примере при приближении Q к P мы получили следующие значения H: 1.8; 1.9 и 1.96. Так как эти числа стремятся к 2, то можно сказать, что наклон графика в точке P равен 2.
- Помните, что наклон графика в данной точке равен производной функции (по которой построен этот график) в этой точке. График отображает перемещение тела с течением времени и, как отмечалось в предыдущем разделе, мгновенная скорость тела равна производной от уравнения перемещения этого тела. Таким образом, можно заявить, что при t = 2 мгновенная скорость равна 2 м/с (это оценочное значение).
Реклама

1
Вычислите мгновенную скорость при t = 4, если перемещение тела описывается уравнением s = 5t³ — 3t² + 2t + 9. Этот пример похож на задачу из первого раздела с той лишь разницей, что здесь дано уравнение третьего порядка (а не второго).
- Сначала вычислим производную этого уравнения:
  
  s = 5t³ — 3t² + 2t + 9
  s = (3)5t^{(3 — 1)} — (2)3t^{(2 — 1)} + (1)2t^{(1 — 1) + (0)9t^{0 — 1}
  15t⁽²⁾ — 6t⁽¹⁾ + 2t^{(0)
  15t⁽²⁾ — 6t + 2}}
- Теперь подставим в уравнение производной значение t = 4:
  
  s = 15t⁽²⁾ — 6t + 2
  15(4)⁽²⁾ — 6(4) + 2
  15(16) — 6(4) + 2
  240 — 24 + 2 = 22 м/с
2
Оценим значение мгновенной скорости в точке с координатами (1,3) на графике функции s = 4t² — t. В этом случае точка P имеет координаты (1,3) и необходимо найти несколько координат точки Q, лежащий близко к точке P. Затем вычислим H и найдем оценочные значения мгновенной скорости.
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
  
  s = 4t² — t
  
  t = 2: s = 4(2)² — (2)
  4(4) — 2 = 16 — 2 = 14, so Q = (2,14)
  
  t = 1.5: s = 4(1.5)² — (1.5)
  4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)
  
  t = 1.1: s = 4(1.1)² — (1.1)
  4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)
  
  t = 1.01: s = 4(1.01)² — (1.01)
  4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704)
- Теперь вычислим H:
  
  Q = (2,14): H = (14 — 3)/(2 — 1)
  H = (11)/(1) = 11
  
  Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
  H = (4.5)/(.5) = 9
  
  Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
  H = (.74)/(.1) = 7.3
  
  Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
  H = (.0704)/(.01) = 7.04
- Так как полученные значения H стремятся к 7, то можно сказать, что мгновенная скорость тела в точке (1,3) равна 7 м/с (оценочное значение).
Реклама

Советы

Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.

Об этой статье

Эту страницу просматривали 83 497 раз.

Была ли эта статья полезной?

Источник

Download Article

Velocity is defined as the speed of an object in a given direction.^[1] In many common situations, to find velocity, we use the equation v = s/t, where v equals velocity, s equals the total displacement from the object’s starting position, and t equals the time elapsed. However, this technically only gives the object’s average velocity over its path. Using calculus, it’s possible to calculate an object’s velocity at any moment along its path. This is called instantaneous velocity and it is defined by the equation v = (ds)/(dt), or, in other words, the derivative of the object’s average velocity equation.^[2]

1
Start with an equation for velocity in terms of displacement. To get an object’s instantaneous velocity, first we have to have an equation that tells us its position (in terms of displacement) at a certain point in time. This means the equation must have the variable s on one side by itself and t on the other (but not necessarily by itself), like this:

s = -1.5t² + 10t + 4
- In this equation, the variables are:
  
  Displacement = s . The distance the object has traveled from its starting position.^[3] For example, if an object goes 10 meters forward and 7 meters backward, its total displacement is 10 — 7 = 3 meters (not 10 + 7 = 17 meters).
  
  Time = t . Self explanatory. Typically measured in seconds.
2
Take the equation’s derivative. The derivative of an equation is just a different equation that tells you its slope at any given point in time. To find the derivative of your displacement formula, differentiate the function with this general rule for finding derivatives: If y = a*xⁿ, Derivative = a*n*x^n-1.This rule is applied to every term on the «t» side of the equation.^[4]
- In other words, start by going through the «t» side of your equation from left to right. Every time you reach a «t», subtract 1 from the exponent and multiply the entire term by the original exponent. Any constant terms (terms which don’t contain «t») will disappear because they be multiplied by 0. This process isn’t actually as hard as it sounds — let’s derive the equation in the step above as an example:
  
  s = -1.5t² + 10t + 4
  (2)-1.5t^(2-1) + (1)10t^{1 — 1} + (0)4t⁰
  -3t¹ + 10t⁰
  -3t + 10
Advertisement
3
Replace «s» with «ds/dt.» To show that our new equation is a derivative of the first one, we replace «s» with the notation «ds/dt». Technically, this notation means «the derivative of s with respect to t.» A simpler way to think of this is just that ds/dt is just the slope of any given point in the first equation. For example, to find the slope of the line made by s = -1.5t² + 10t + 4 at t = 5, we would just plug «5» into t in its derivative.
- In our running example, our finished equation should now look like this:
  
  ds/dt = -3t + 10
4
Plug in a t value for your new equation to find instantaneous velocity.^[5] Now that you have your derivative equation, finding the instantaneous velocity at any point in time is easy. All you need to do is pick a value for t and plug it into your derivative equation. For example, if we want to find the instantaneous velocity at t = 5, we would just substitute «5» for t in the derivative ds/dt = -3 + 10. Then, we’d just solve the equation like this:

ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 meters/second
- Note that we use the label «meters/second» above. Since we’re dealing with displacement in terms of meters and time in terms of seconds and velocity in general is just displacement over time, this label is appropriate.

1
Graph your object’s displacement over time. In the section above, we mentioned that derivatives are just formulas that let us find the slope at any point for the equation you take the derivative for.^[6] In fact, if you represent an object’s displacement with a line on a graph, the slope of the line at any given point is equal to the object’s instantaneous velocity at that point.^[7]
- To graph an object’s displacement, use the x axis to represent time and the y axis to represent displacement. Then, just plot points by plugging values for t into your displacement equation, getting s values for your answers, and marking the t,s (x,y) points on the graph.
- Note that the graph can extend below the x axis. If the line representing your object’s motion drops below the x axis, this represents your object moving behind where it started. Generally, your graph won’t extend behind the y axis — we don’t often measure velocity for objects moving backward in time!
2
Choose one point P and a point Q that is near it on the line. To find a line’s slope at a single point P, we use a trick called «taking a limit.» Taking a limit involves taking two points (P, plus Q, a point near it) on the curved line and finding the slope of the line linking them over and over again as the distance between P and Q gets smaller.
- Let’s say that our displacement line contains the points (1,3) and (4,7). In this case, if we want to find the slope at (1,3), we can set (1,3) = P and (4,7) = Q.
3

Find the slope between P and Q. The slope between P and Q is the difference in y-values for P and Q over the difference in x-values for P and Q. In other words, H = (y_Q — y_P)/(x_Q — x_P), where H is the slope between the two points. In our example, the slope between P and Q is:

H = (y_Q — y_P)/(x_Q — x_P)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33
4

Repeat several times, moving Q nearer to P. Your goal here is to make the distance between P and Q smaller and smaller until it gets close to a single point. The smaller the distance between P and Q gets, the closer the slope of your tiny line segments will be to the slope at point P. Let’s do this a few times for our example equation, using the points (2,4.8), (1.5,3.95), and (1.25,3.49) for Q and our original point of (1,3) for P:

Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8

Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9

Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96
5
Estimate the slope for an infinitely small interval on the line. As Q gets closer and closer to P, H will get closer and closer to the slope at point P. Eventually, at an infinitely small interval, H will equal the slope at P. Because we aren’t able to measure or calculate an infinitely small interval, we just estimate the slope at P once it’s clear from the points we’ve tried.^[8]
- In our example, as we moved Q closer to P, we got values of 1.8, 1.9, and 1.96 for H. Since these numbers appear to be approaching 2, we can say that 2 is a good estimate for the slope at P.
- Remember that the slope at a given point on a line is equal to the derivative of the line’s equation at that point. Since our line is showing our object’s displacement over time and, as we saw in the section above, an object’s instantaneous velocity is the derivative of its displacement at a given point, we can also say that 2 meters/second is a good estimate for the instantaneous velocity at t = 1.

1
Find the instantaneous velocity at t = 4 given the displacement equation s = 5t³ — 3t² + 2t + 9. This is just like our example in the first section, except that we’re dealing with a cubic equation rather than a quadratic equation, so we can solve it in the same way.
- First, we’ll take our equation’s derivative:
  
  s = 5t³ — 3t² + 2t + 9
  s = (3)5t^{(3 — 1)} — (2)3t^{(2 — 1)} + (1)2t^{(1 — 1) + (0)9t^{0 — 1}
  15t⁽²⁾ — 6t⁽¹⁾ + 2t^{(0)
  15t⁽²⁾ — 6t + 2}}
- Then, we’ll plug in our value for t (4):
  
  s = 15t⁽²⁾ — 6t + 2
  15(4)⁽²⁾ — 6(4) + 2
  15(16) — 6(4) + 2
  240 — 24 + 2 = 218 meters/second
2
Use graphical estimation to find the instantaneous velocity at (1,3) for the displacement equation s = 4t² — t. For this problem, we’ll use (1,3) as our P point, but we’ll have to find a few other points near it to use as our Q points. Then, it’s just a matter of finding our H values and making an estimation.
- First, let’s find Q points at t = 2, 1.5, 1.1 and 1.01.
  
  s = 4t² — t
  
  t = 2: s = 4(2)² — (2)
  4(4) — 2 = 16 — 2 = 14, so Q = (2,14)
  
  t = 1.5: s = 4(1.5)² — (1.5)
  4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)
  
  t = 1.1: s = 4(1.1)² — (1.1)
  4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)
  
  t = 1.01: s = 4(1.01)² — (1.01)
  4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704)
- Next, let’s get our H values:
  
  Q = (2,14): H = (14 — 3)/(2 — 1)
  H = (11)/(1) = 11
  
  Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
  H = (4.5)/(.5) = 9
  
  Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
  H = (.74)/(.1) = 7.3
  
  Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
  H = (.0704)/(.01) = 7.04
- Since our H values seem to be getting very close to 7, we can say that 7 meters/second is a good estimate for the instantaneous velocity at (1,3).

Add New Question

Question

What is the difference between instantaneous and average velocity?

Instantaneous is at that moment, whereas average is the mean of the entire time span.
Question

How do I calculate instantaneous acceleration?

Instantaneous acceleration can be considered as the value of the derivative of the instantaneous velocity. For example:

s = 5(t^3) — 3(t^2) + 2t + 9
v = 15(t^2) — 6t + 2
a = 30t — 6

If we want to know the instantaneous acceleration at t = 4, then a(4) = 30 * 4 — 6 = 114 m/(s^2)
Question

When is instantaneous velocity and average velocity the same?

Instantaneous velocity tells you the velocity of an object at a single moment in time. If the object is moving with a constant velocity, then the average velocity and instantaneous velocity will be the same. In all situations, they are not likely to be the same.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

To find acceleration (the change in velocity over time), use the method in part one to get a derivative equation for your displacement function. Then, take another derivative, this time of your derivative equation. This will give you an equation for finding acceleration at a given time — all you have to do is plug in your value for time.
The equation which relates Y (displacement) to X (time) might be really simple, like, for instance, Y= 6x + 3. In this case the slope is constant and it is not necessary to find a derivative to find the slope, which is, following the Y = mx + b basic model for linear graphs, 6.
Displacement is like distance but it has a set direction, this makes displacement a vector and speed a scalar. Displacement can be negative while distance will only be positive.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate instantaneous velocity, start with an equation for velocity in terms of displacement, which should have an «s» on one side for displacement and a «t» on the other for time. Then, take the equation’s derivative and replace the «s» with the notation «ds» over «dt.» Finally, plug in a «t» value and solve the equation to find the instantaneous velocity at any point in time. To learn how to estimate instantaneous velocity graphically, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,051,180 times.

Did this article help you?

Источник

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

расстояние, которое проходит тело, много больше его размера;
расстояние от данного тела до другого тела много больше его размера;
тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Содержание

Механическое движение и его виды
Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
Скорость
Ускорение
Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
Прямолинейное равноускоренное движение
Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение по окружности с постоянной по модулю скоростью
Основные формулы по теме «Кинематика»

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

прямолинейным — это движение, траектория которого прямая линия;
криволинейным — это движение, траектория которого кривая линия;

3. по скорости

равномерным — движение, при котором скорость тела с течением времени не изменяется;
неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ( v ), единицы измерения — м/с (км/ч).

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ( a ), единица измерения — м/с².
В векторном виде:

где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

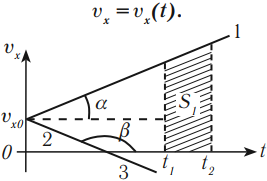
График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ( g ), единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

равномерного движения по горизонтали;
равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с².

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.

где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.

Основные формулы по теме «Кинематика»

Кинематика

3 (60.29%) 140 votes

Источник

Мгновенная скорость сообщает нам о движении частицы в определенный момент времени в любом месте на ее пути.

Мгновенная скорость принимается за предел средней скорости при стремлении времени к нулю. Вычислять V_инст мы можем использовать график смещения-времени / формулу мгновенной скорости. т.е. производная смещения (s) по времени (t), взятая.

Чтобы узнать, как рассчитать мгновенную скорость объекта, нам нужно выполнить следующие действия.. Давайте посмотрим на это на примере.

Рассмотрим уравнение скорости в терминах положения / смещения.

Вычислять мгновенная скорость, мы должны рассмотреть уравнение это говорит нам о его должность ‘s’ в определенный время ‘t’. Это означает, что уравнение должно содержать переменную ‘s‘с одной стороны и’t‘ с другой стороны,

s = -2т² + 10т +5 при t = 2 секунды.

В этом уравнении переменными являются:

Смещение = s, измеряется в метрах.

Время = t, измеряется в секундах.

Рассмотрим производную данного уравнения.

Чтобы найти производную данного уравнения перемещения, дифференцировать функцию по времени,

ds / dt = — (2) 2т ^(2-1) + (1) 10 т^{1 – 1} + (0) 5 т⁰

ds / dt = -4т¹ + 10т⁰

ds / dt = -4t + 10

Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.

Найдите мгновенная скорость при t = 2 подставить «2» для t в производной ds / dt = -4t + 10. Тогда мы можем решить уравнение

ds / dt = -4t + 10

ds / dt = -4 (2) + 10

ds / dt = -8 + 10

ds / dt = -2 метра в секунду

Здесь «метры / секунда» — это единица измерения мгновенной скорости в системе СИ.

Как рассчитать Instantaneoскорость нас из графика

Мгновенная скорость в любой конкретный момент времени определяется наклоном касательной, проведенной к графику положения-времени в этой точке.

Постройте график расстояние против времени.
Отметьте точку, в которой вам нужно найти мгновенную скорость, скажем A.
Определите точку на графике, соответствующую времени t₁и t₂.
Вычислить v_{средний} и проведем касательную в точке A.
На графике v_инст в точке A находится по касательной, проведенной в этой точке

Чем длиннее тангенс, тем точнее будут значения.
На показанном изображении Синяя линия это график зависимости положения от времени, А Красная линия — приблизительный наклон линии при t = 2.5 секунды.

Если мы продолжаем выбирать точки, которые все ближе и ближе друг к другу, линия начнет приближаться к наклону линии, касательной к одной точке.
Если мы возьмем предел функции в этой точке, мы получим значение наклона касательной в этой точке.
Расстояние составляет примерно 140 м, а временной интервал — 4.3 с. Следовательно, приблизительный уклон составляет 32.55 м / с.

Как рассчитать мгновенную скорость по графику положения-времени.

Для вычисления мгновенной скорости по графику положения-времени.

Постройте график зависимости смещения от времени.

Используйте оси X и Y для представления время и перемещение.
Затем нанесите на график значения времени и смещения.

Выберите любые две точки на графике st.

Линия смещения содержит точки (3,6) и (5,8).
В этом примере, если мы хотим найти наклон в точке (3,6), мы можем установить А = (3,6) и B = (5,8)

Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.

Найдите среднюю скорость между этими двумя временными интервалами, т. Е.

где K — наклон между двумя точками.

Здесь наклон между A и B равен:

Slope = k= (8-6)/(5-3)=1

Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.

Продолжайте выбирать точки ближе друг к другу; затем он начнет приближаться к наклону касательной.
Если мы рассмотрим предел функции в этой точке, мы получим значение наклона в этой точке.
Здесь мы можем использовать точки (4,7.7), (3.5, 6.90) и (3.25, 6.49) для B и исходную точку (3,6) для A.

При B = (4,7.7)

При B = (3.5; 6.90)

При B = (3.25; 6.49)

Вычислите наклон для бесконечно малого отрезка касательной.

В этом примере, когда мы приближаем B к A, мы получаем значения 1.7, 1.8 и 1.96 для K. Поскольку эти числа примерно равны 2, можно сказать, что 2 — наклон А.

Здесь, мгновенная скорость 2 м / с.

Формула мгновенной скорости

С математической точки зрения мы можем написать формула мгновенной скорости в виде,

Instantaneous Velocity= Change in position/ Time Interval

Здесь, ds / dt — это производная смещения (с) по времени (t).

Приведенные выше производная имеет конечное значение когда и знаменатель, и числитель стремятся к нулю.

Расчет формулы мгновенной скорости

Используя вычисления, всегда можно вычислить скорость объекта в любой момент на его пути. Это называется мгновенной скоростью. и задается уравнением v = ds / dt.

Мгновенная скорость = предел, поскольку изменение во времени приближается к нулю (изменение положения / изменение во времени) = производная смещения по времени

Формула средней и мгновенной скорости

	Формула	Символ	Определение
Средняя скорость		s_f = Окончательный смещение s_i₌Начальное смещение t_f₌ Последний раз t_i = Начальное время	Средняя скорость is общее расстояние деленное на общее затраченное время.
Мгновенная скорость			Скорость при любом момент времени.

Формула мгновенной угловой скорости

Компания мгновенная угловая скорость скорость, с которой частица движется по круговой траектории в определенный момент времени.

Компания мгновенная угловая скорость вращающегося объекта определяется выражением

dθ/dt = производная углового положения θ по времени, найденное предельным переходом Δ t → 0 в средняя угловая скорость.

Компания направление угловой скорости на круговой траектории — вдоль оси вращения и указывает от вас на вращающееся тело по часовой стрелке и к вам для тела, вращающегося против часовой стрелки. В математике это обычно описывается правило правой руки.

Формула мгновенной скорости и скорости

Формула мгновенной скорости

Instantaneous Speed=ds/dt

Разница между мгновенной скоростью и мгновенной скоростью.

Мгновенная скорость	Мгновенная скорость
Это скорость движущейся частицы в определенный момент t.	Вход в музей Мадам Тюссо мера скорости частицы в определенный момент t.
Мгновенная скорость определяет, насколько быстро и в каком направлении движется объект.	Мгновенная скорость измеряет, насколько быстро частица движется.
Количество векторов	Скалярная величина

Определение и формула мгновенной скорости

Определение мгновенной скорости

Мгновенная скорость описывается как скорость движущегося объекта. Мы можем найти его, используя среднюю скорость, но мы должны сузить время, чтобы приблизиться к нулю.

Итого можно сказать, что мгновенная скорость — это скорость движущейся частицы в определенный момент времени.

Формула мгновенной скорости

Для любого уравнения движения s(t), для мгновенная скорость когда t приближается к нулю, мы можем записать формула в виде,

Мгновенная скорость формула предела

Мгновенная скорость любого объекта — это предел средней скорости, когда время приближается к нулю..

Вставьте значения t₁= t и t₂ = t + Δt в уравнение для средней скорости и переходя к пределу при Δt → 0, находим формула предела мгновенной скорости

Как найти мгновенную скорость на графике

Мгновенная скорость равна наклону касательной на графике положение-время.

Мгновенноs Интерпретация скорости из графика st

Мгновенная скорость равна наклону касательной на графике положение-время.
Интерпретация мгновенной скорости по графику st

Наклон фиолетовой линии (касательной) на графике смещения v / s дает мгновенную скорость.
Если фиолетовая линия образует угол с положительной осью абсцисс.

V_inst = наклон фиолетовой линии = tanθ

Как найти мгновенную скорость из средней скорости

Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.

Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить V_inst_.

Пример мгновенной скорости

Во время езды на велосипеде велосипедист меняет свою скорость в зависимости от расстояния и времени, которое он проходит.

Велосипедисты катаются на велосипеде, Изображение предоставлено: Автор изображения pxfuel.com

Если мы хотим найти скорость в одной конкретной точке, мы должны использовать мгновенную скорость.

Покажи нам пример,

а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?

Решение:

Данный с = 4т² + 2т + 3

Дифференцируя данную функцию по времени, мы вычисляем мгновенную скорость следующим образом:

Подставляя значение t = 2, мы получаем мгновенную скорость как,

V_{моментальный}=ds/dt

Подставляя функцию s,

v_инст =d(4t² +2t +3)/dt

v_инст =8t+2

v_инст = (8 * 2)+2v_инст =18 ms^-1

Таким образом, мгновенная скорость для вышеуказанной функции составляет 18 м / с.

Проблема мгновенной скорости

Некоторые проблемы с мгновенной скоростью,

Проблема 1:

Движение тележки задается функцией s = 3t² + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.

Решение:

Данная функция s = 3t²+ 10т + 5.

Продифференцируя указанную выше функцию по времени, получим

V_{моментальный}=ds/dt=d(3t²+10t +5)/dt

Подставляя функцию s,

V_{моментальный} = v(t)=6t+10

Подставляя значение t = 4 с, мы получаем мгновенную скорость как,

v(4)= 6(4)+10

v(4) =34ms^-1

Для данной функции мгновенная скорость составляет 34 м / с.

Проблема 2:

Выстреленная пуля движется по прямой траектории, и ее уравнение движения имеет вид S (t) = 3t + 5t.². Так, например, если он летит за 12 секунд до удара, найдите мгновенную скорость при t = 7 с.

Решение: Мы знаем уравнение движения:

s(t) = 3t + 5t²

V_{моментальный}=ds/dt=d(3t + 5t²)/dt=3+10t

V_{моментальный}at (t = 7) = 3 + (10 * 7)

V_{моментальный} = 73 м / с

Проблема 3:

Объект выпускается с определенной высоты, чтобы он мог свободно падать под действием силы тяжести. Уравнение движения для перемещения s (t) = 5.1 т.². Какой будет мгновенная скорость объекта в момент времени t = 6 с после выпуска?

Изображение предоставлено PXHere.com

Решение:

Уравнение движения:

s (t) = 5.1 т²

Мгновенная скорость при t = 6 с

Проблема 4:

Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t³ — 3т² + 2т + 7.

Решение:

Это похоже на предыдущие задачи, за исключением того, что они дали кубическое уравнение вместо квадратного уравнения, чтобы решить его таким же образом.

Уравнение движения:

s (t) = 3t³ — 3т² + 2т + 7.

Мгновенная скорость при t = 7 с

v_инст = 9 (7)² – 6(7) +2

v_инст = 441 – 42 +2

v_инст = 401 м / с

Проблема 5:

Положение человека, движущегося по прямой, определяется выражением s (t) = 7t.²+ 3t + 19, где t — время (секунды). Найдите уравнение для мгновенной скорости v (t) частицы в момент времени t.

Решение:

Дано: s (t) = 7t²+ 3т + 19

v_инст = ds/dt =d(7t² + 3t+19)/dt

v_инст = 14t + 3

v_инст = v (t) = (14t + 3) м / с — уравнение для мгновенной скорости.

Предположим, что если принять t = 3s, то

v_инст = v(t)= 14(3) + 3 = 45m/s

Проблема 6:

Движение автомобиля описывается уравнением движения s = gt² + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.

Решение:

s (t) = gt² + b

v (t) = 2gt + 0

v (t) = 2gt

Здесь g = 12 и t = 4s,

v (4) = [2 x 12 x 4] = 96 м / с.

v (т) = 96 м / с.

Проблема 7:

Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т.². Затем вычислите мгновенную скорость стола на 3 с?

Решение:

Мгновенная скорость при t = 3 с составляет -72 м / с.

Проблема 8:

Функция положения частиц определяется выражением s = (3t²)_i — (4т)_k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?

Решение:

s (t) = (3т²)_i — (4т)_k +2

v (t) = (6t)_i -4_k………… .. (Уравнение 1)

v (2) = (6 * 2)_i -4_k

v (2) = 12_i -4_k м/с

Чтобы вычислить мгновенное ускорение как функцию времени

а (т) = v¹(Т)

дифференцируя уравнение 1 по t, получаем

а (т) = 6_i м/с

Проблема 9:

Положение насекомого определяется как s = 44 + 20t — 3t.³, где t в секундах, а s в метрах.

а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.

б. В какое время между 0 и 4 мгновенная скорость равна нулю.

решение:

Для расчета средней скорости

Чтобы найти время, при котором мгновенная скорость равна нулю.

v_инст =ds/dt=20-9t²

20-9t²=0

t=(20/9)^½

т=1.49 с

Проблема 10:

Частица движется с функцией смещения s = t² + 3.

Найдите положение при t = 2.

Найдите среднюю скорость от t = 2 до t = 3.

Найти его мгновенную скорость при t = 2.

Решение:

Чтобы найти позицию при t = 2

s (t) = t² + 3

с (2) = (2)² + 3

с (2) = 7

Для того, чтобы найти Средняя скорость.

Чтобы найти мгновенную скорость

v_инст = ds / dt

v_инст =2t

При t = 2 с

v_инст =2(2)=4m/s

Мгновенная скорость в зависимости от средней скорости

Мгновенная скорость	Средняя скорость
Компания мгновенная скорость — средняя скорость между двумя точками.	Средняя скорость это соотношение изменения дистасть относительно времени за период.
Мгновенная скорость рассказывает о движении между двумя точками на пройденном пути.	Средняя скорость не дает информации о движении между точками. Путь может быть прямым / изогнутым, а движение может быть постоянным / переменным.
Мгновенная скорость равен наклону касательной к смещение (с) в зависимости от графика времени.	Он равен наклону секущая линия of граф st.
вектор	вектор

Как найти мгновенная скорость без исчисления

Wмы можем найти мгновенную скорость приближением по график зависимости смещения от времени без исчисления в определенной точке. Нам нужно провести касательную в точке вдоль изогнутой линии и оценить наклон, где вам нужно найти мгновенную скорость.

Как рассчитать мгновенную скорость и мгновенное ускорение

	Мгновенная скорость	Мгновенное ускорение
Из формулы	Для расчета мгновенной скорости, возьмем предел изменения расстояния по времени, когда время приближается к нулю. т. е. взяв первая производная функции смещения.	к рассчитать мгновенное ускорение, принять предел изменения скорости по времени, когда изменение во времени приближается к нулю. т.е. взяв вторая производная функции смещения.
Из графика	Равно наклон касательной к графику st.	Равно наклон касательной графика vt.

11 задачи:

Пуля, выпущенная в космос, движется по прямой траектории, и ее уравнение движения имеет вид s (t) = 2t +4t². Если он движется в течение 12 секунд до удара, найдите мгновенную скорость и мгновенное ускорение в момент времени t = 3 секунды.

Решение: Мы знаем уравнение движения: s (t) = 2t + 4t²

v_инст = ds/dt= 2t + 4t²/dt=2+8t

v_инст at t=7

v(t=7)=2+((8X3)

v_инст = 26 м / с

a(t)=dv/dt=d(2+8t)/dt=8

a(t)=8m/s

Как найти мгновенную скорость и скорость

Мгновенная скорость задается как величина мгновенной скорости.

Если известно перемещение как функция времени, мы можем найти мгновенная скорость в любое время.

Давайте разберемся в этом на примере.

12 задачи:

Уравнение движения s (t) = 3t³

Instantaneous Speed= ds/dt

s_инст =d3t³/dt=9t²

Рассмотрим t = 2s

s_инст = 9 (2)²= 36 м / с

Почему можно рассчитать мгновенную скорость по кинематическим формулам только при постоянном ускорении

Уравнения кинематики можно использовать только при постоянном ускорении объекта.

В случае переменные ускорения, Уравнения кинематики будут разными в зависимости от функции, которую принимает ускорение; в то время; мы должны использовать Комплексный подход вычислять мгновенная скорость. Что будет немного сложно.

Почему при вычислении мгновенной скорости мы берем небольшие промежутки времени. Как он дает скорость в этот момент, если мы рассчитываем ее за определенный промежуток времени?

Компания мгновенная скорость дан кем-то,

Чем меньше значение «t», Тем точнее будет наклон касательной, т. е. мгновенная скорость.

Когда ты хочешь рассчитать скорость в определенное время вам нужно сначала рассчитать средние скорости взяв небольшие промежутки времени. Если эти средние скорости дают одно и то же значение, тогда это будет требуемый мгновенная скорость.

Различаются ли скорость и мгновенная скорость?

Мгновенная скорость отличается от скорости.

Скорость обычно известен как скорость изменения положения во времени. Напротив, в мгновенная скорость, временной интервал сужается, чтобы приблизиться к нулю, чтобы получить скорость в конкретный момент времени.

Например,

Частица движение по кругу имеет нулевые смещения, и требуется знать скорость частицы. В этом случае мы можем вычислить мгновенную скорость, потому что она имеет тангенциальная скорость в любой момент времени.

Что такое мгновенная скорость на реальных примерах

Реальные примеры мгновенной скорости

Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; на тот момент полное водоизмещение и средняя скорость будет равна нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.

Игра в сквош, пример мгновенной скорости Изображение предоставлено: Изображение предоставлено pixabay.com

Спидометр автомобиля дает информацию о мгновенная скорость / скорость средство передвижения. Он показывает скорость в определенный момент времени.

Спидометр, Изображение предоставлено: Автор изображения pxfuel.com

Во время гонки фотографы делают снимки бегунов, их средняя скорость не меняется, но меняется их мгновенная скорость, зафиксированная на «снимках». Так что это будет пример мгновенной скорости.

Изображение предоставлено Commons Wikimedia.org, СС по 2.0 Generic

Если вы находитесь рядом с магазином, и перед вами проехал автомобиль на отметке «t«Во-вторых, и вы начинаете думать о его скорости на конкретном время, здесь вы имели бы в виду мгновенная скорость транспортного средства.

Часто задаваемые вопросы | FAQs

Является ли мгновенная скорость вектором

Мгновенная скорость — это векторная величина.

Мгновенная скорость — это вектор, потому что он имеет как величину, так и направление. Он показывает как скорость (относится к величине), так и направление. участникале Имеет размер LT^-1Мы можем определить это, взяв наклон графика расстояние-время..

Как найти мгновенную скорость только с графиком положения и времени и без заданного уравнения

Мы можем определить мгновенную скорость, взяв наклон графика положения-времени.

Постройте график смещения во времени.
Выберите точку A и другую точку B, которая находится рядом с точкой A на линии.
Найдите угол наклона между A и B, рассчитайте несколько раз, перемещая A ближе к B.
Рассчитайте наклон для бесконечно малого интервала на прямой.
Полученный наклон представляет собой мгновенную скорость.

Можно ли мгновенно изменить скорость

Невозможно вызвать мгновенное изменение скорости, так как для этого потребуется бесконечное ускорение.

Как правило, ускорение является результатом F = ma

a=F/m=Force over a mass

а скорость является результатом ускорения (от интегрирования). Если изменение скорости является ступенчатой функцией и когда время приближается к нулю, потребуется бесконечное ускорение и сила, чтобы мгновенно изменить скорость массы.

Как я могу рассчитать смещение, если ускорение является функцией мгновенной скорости Задана начальная скорость

Мы можем вычислить смещение двумя способами, когда задана начальная скорость.

От происхождения

Здесь ускорение является функцией мгновенной скорости,

а=дв/дт

Начальная скорость

v=дс/дт

a=d(ds)/dt²

d(ds)=adt²

Интегрируя,

Используя эту форму, вы можете получить ds смещения.

Из формулы

Используя приведенное ниже кинематическое уравнение, мы можем найти смещение,

[S = ut + 1/2(at²)]

Что такое средний и мгновенная скорость

Средняя скорость и мгновенная скорость выражаются следующим образом:

Средняя скорость	Мгновенная скорость
Средняя скорость для определенного временного интервала — это полное смещение, деленное на общее время.	И временной интервал, и смещение в какой-то момент приближаются к нулю. Но предел производной смещения по общему интервалу времени отличен от нуля и называется мгновенной скоростью.
Средняя скорость это скорость всего пути в движении	а мгновенная скорость скорость частицы в определенный момент времени
v`_avg` = `s/t`	v`_inst` = `ds/dt`

Мгновенное ускорение перпендикулярно мгновенной скорости

Мгновенное ускорение тела всегда перпендикулярно мгновенной скорости.

При круговом движении мгновенная ускорение тела всегда перпендикулярно мгновенной скорости, и это ускорение называется центростремительным. ускорение. Скорость остается неизменной; изменяется только направление, поскольку перпендикулярное ускорение изменяет траекторию тела.

Источник

Алгебра и начала математического анализа, 11 класс

Урок №19. Решение задач с помощью производной.

Перечень вопросов, рассматриваемых в теме

механический смысл первой производной;
механический смысл второй производных;
скорость и ускорение.

Глоссарий по теме

Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).

Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.

Производная от производной называется второй производной или производной второго порядка и обозначается fили

Производная от второй производной называется производной третьего порядка и обозначается или f»’(x). Производную n-го порядка обозначают f⁽ⁿ⁾ (x) или y⁽ⁿ⁾.

Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть

Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним механический смысл производной:

Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).

Пример 1. Точка движется прямолинейно по закону (S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.

Решение:

скорость прямолинейного движения равна производной пути по времени, то есть .

Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).

Ответ: 20 м/c.

Пример 2. Маховик, задерживаемый тормозом, поворачивается за tс на угол

Найдите:

а) угловую скорость вращения маховика в момент t = 6 с;

б) в какой момент времени маховик остановится?

Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t²)=4-0,4t.

Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).

б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.

Ответ: угловая скорость маховика равна (рад/с); t=10 c.

Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t²+2t-5. Найти кинетическую энергию тела через 3 с после начала движения.

Решение: найдём скорость движения тела в любой момент времени t.

v= S’=(3t²+2t-5)’=6t+2

Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..

Определим кинетическую энергию тела в момент времени t=3.

Ответ: Е=1200 Дж

Производная второго порядка. Производная n-го порядка.

Производная от производной называется второй производной или производной второго порядка и обозначается .

Производная от второй производной называется производной третьего порядка и обозначается y»’ или f»'(x) Производную n-го порядка обозначают f⁽ⁿ⁾ (x) или y⁽ⁿ⁾.

Примеры. Найдем производные четвёртого порядка для заданных функций:

1) f(x)= sin 2x

f'(x)=cos 2x∙(2x)’= 2cos 2x

f (x)=-2sin2x∙(2x)’=-4sin 2x

f»'(x)= -4 cos 2x∙(2x)= -8 cos 2x

f⁽⁴⁾(x)= 8 sin2x∙(2x)’= 16 sin 2x

2) f(x)=2^3x

f’(x)=3∙ 2^3x ∙ln2

f (x)= 9∙ 2^3x ∙ln²2

f»'(x)= 27∙ 2^3x ∙ln³2

f⁽⁴⁾(x)= 81∙ 2^3x ∙ln⁴2

Механический смысл второй производной.

Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)

Пример 4. Точка движется прямолинейно по закону S(t)= 3t²-3t+8. Найти скорость и ускорение точки в момент t=4 c.

Решение:

найдём скорость точки в любой момент времени t.

v=S’=(3t²-3t+8)’=6t-3.

Вычислим скорость в момент времени t=4 c.

v(4)=6∙4-3=21(м/с)

Найдём ускорение точки в любой момент времени t.

a= v’= (6t-3)’=6 и a(4)= 6 (м/с²) , то есть ускорение в этом случае является величиной постоянной.

Ответ: v=21(м/с); a= v’= 6 (м/с²).

Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t³-3t²+5. Найти силу, действующую на тело в момент времени t=4 c.

Решение: сила, действующая на тело, находится по формуле F=ma.

Найдём скорость движения точки в любой момент времени t.

v=S’=(t³-3t²+5)’=3t²-6t.

Тогда v(4)=3∙4²-6∙4=24 (м/с).

Найдём ускорение: a(t)=v’=(3t²-6t)’=6t-6.

Тогда a(4)= 6∙4-6= 18 (м/с²).

F=ma=3∙18= 54 Н

Ответ: F= 54 Н

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Напишите производную третьего порядка для функции:

f(x)= 3cos4x-5x³+3x²-8

_____________________

Решим данную задачу:

f’’’(x)=( 3cos4x-5x³+3x²-8)’’’=(((3cos4x-5x³+3x²-8)’)’)’=((-12sin4x-15x²+6x)’)’=(-48cos4x-30x)’=192sin4x-30.

Ответ: 192sin4x-30

№ 2. Тип задания: выделение цветом

Точка движется прямолинейно по закону S(t)= 3t²+2t-7. Найти скорость и ускорение точки в момент t=6 c.

v=38 м/с; a=6 м/с²
v=38 м/с; a=5 м/с²
v=32 м/с; a=6 м/с²
v=32 м/с; a=5 м/с²

Решим данную задачу:

Воспользуемся механическим смыслом второй производной:

v= S’(t)=( 3t²+2t-7)’=6t+2.

Вычислим скорость в момент времени t=6 c.

v(6)=6∙6+2=38 (м/с)

Найдём ускорение точки в любой момент времени t.

a= v’= (6t+2)’=6 и a(6)= 6 (м/с²) , то есть ускорение в этом случае является величиной постоянной.

Ответ: v=38(м/с); a= v’= 6 (м/с²).

Верный ответ:

v=38 м/с; a=6 м/с²
v=38 м/с; a=5 м/с²
v=32 м/с; a=6 м/с²
v=32 м/с; a=5 м/с²

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Video

References

About This Article

Did this article help you?

Кинематика

Механическое движение и его виды

Относительность механического движения

Правило сложения перемещений

Правило сложения скоростей

Относительная скорость

Скорость

Ускорение

Равномерное движение

График скорости (проекции скорости)

График перемещения (проекции перемещения)

Прямолинейное равноускоренное движение

Свободное падение (ускорение свободного падения)

Движение тела по вертикали

Движение тела, брошенного горизонтально

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение по окружности с постоянной по модулю скоростью

Основные формулы по теме «Кинематика»

Рассмотрим уравнение скорости в терминах положения / смещения.

Рассмотрим производную данного уравнения.

Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.

Как рассчитать Instantaneoскорость нас из графика

Как рассчитать мгновенную скорость по графику положения-времени.

Постройте график зависимости смещения от времени.

Выберите любые две точки на графике st.

Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.

Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.

Вычислите наклон для бесконечно малого отрезка касательной.

Формула мгновенной скорости

Расчет формулы мгновенной скорости

Формула средней и мгновенной скорости

Формула мгновенной угловой скорости

Формула мгновенной скорости и скорости

Разница между мгновенной скоростью и мгновенной скоростью.

Определение и формула мгновенной скорости

Определение мгновенной скорости

Формула мгновенной скорости

Мгновенная скорость формула предела

Как найти мгновенную скорость на графике

Мгновенноs Интерпретация скорости из графика st

Как найти мгновенную скорость из средней скорости

Пример мгновенной скорости

а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?

Проблема мгновенной скорости

Некоторые проблемы с мгновенной скоростью,

Проблема 1:

Движение тележки задается функцией s = 3t2 + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.

Проблема 2:

Проблема 3:

Проблема 4:

Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t3 — 3т2 + 2т + 7.

Проблема 5:

Проблема 6:

Движение автомобиля описывается уравнением движения s = gt2 + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.

Проблема 7:

Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т.2. Затем вычислите мгновенную скорость стола на 3 с?

Проблема 8:

Функция положения частиц определяется выражением s = (3t2)i — (4т)k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?

Проблема 9:

Положение насекомого определяется как s = 44 + 20t — 3t.3, где t в секундах, а s в метрах.

а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.

б. В какое время между 0 и 4 мгновенная скорость равна нулю.

Для расчета средней скорости

Чтобы найти время, при котором мгновенная скорость равна нулю.

Проблема 10:

Частица движется с функцией смещения s = t2 + 3.

Найдите положение при t = 2.

Найдите среднюю скорость от t = 2 до t = 3.

Найти его мгновенную скорость при t = 2.

Чтобы найти позицию при t = 2

Для того, чтобы найти Средняя скорость.

Чтобы найти мгновенную скорость

Мгновенная скорость в зависимости от средней скорости

Движение тележки задается функцией s = 3t² + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.

Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t³ — 3т² + 2т + 7.

Движение автомобиля описывается уравнением движения s = gt² + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.

Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т.². Затем вычислите мгновенную скорость стола на 3 с?

Функция положения частиц определяется выражением s = (3t²)_i — (4т)_k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?

Положение насекомого определяется как s = 44 + 20t — 3t.³, где t в секундах, а s в метрах.

Частица движется с функцией смещения s = t² + 3.