Перейти к контенту
Условие задачи:
Автомобиль движется со скоростью 12 м/с. Чему равен модуль линейной скорости верхней точки протектора колеса автомобиля относительно земли?
Задача №1.7.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(upsilon=12) м/с, (upsilon_в-?)
Решение задачи:
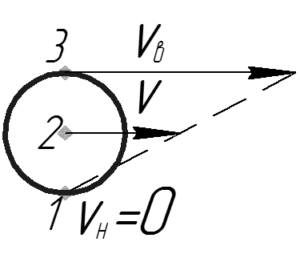
При таком движении всегда существует точка, скорость которого в данный момент времени равна нулю. Если колесо не проскальзывает, то такой точкой является точка касания колеса с дорогой (точка 1 на рисунке). Эту точку также называют мгновенный центром скоростей (МЦС).
Интересно, что в этот момент времени все точки колеса совершают вращательное движение (естественно с одной угловой скоростью) вокруг МЦС. Поэтому верно записать следующее:
[left{ begin{gathered}
upsilon = omega cdot R hfill \
{upsilon _в} = omega cdot 2R hfill \
end{gathered} right.]
(R) – это радиус колеса.
Тогда очевидно, что:
[{upsilon _в} = 2upsilon ]
[{upsilon _в} = 2 cdot 12 = 24; м/с]
Ответ: 24 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.23 Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после
1.7.25 Человек бежит со скоростью 5 м/с относительно палубы теплохода в направлении
1.7.26 При движении моторной лодки по течению реки ее скорость относительно берега
( 6 оценок, среднее 4 из 5 )
Сообщения без ответов | Активные темы | Избранное
|
|
Движени по окружности
|
|
14/11/09 |
Какую линейную скорость имеет верхняя точка обода велосипедного колеса, если велосипедист едет по горизонтальной дороге с постоянной скоростью 20 км/ч?
|
|
|
|
|
gris |
Re: Движени по окружности
|
||
13/08/08 |
Скорости векторно складываются. Со скоростью 20 км/ч двигается центр колеса. А для нахождения скорости точек обода надо ещё прибавить и скорость этих точек относительно центра. В самой верхней и самой нижней точке эта скорость по модулю будет такой же, а вот по направлению -?
|
||
|
|
|||
|
1rome1 |
Re: Движени по окружности
|
|
14/11/09 |
. А для нахождения скорости точек обода надо ещё прибавить и скорость этих точек относительно центрах Вот только как вычислить скорость точек относительно центра?
|
|
|
|
|
BISHA |
Re: Движени по окружности
|
||
08/01/09 |
Какую линейную скорость имеет верхняя точка обода велосипедного колеса, если велосипедист едет по горизонтальной дороге с постоянной скоростью 20 км/ч? 20 км/ч — если без проскальзывания.
|
||
|
|
|||
|
Батороев |
Re: Движени по окружности
|
|
23/01/07 |
Верхняя точка обода колеса имеет скорость 40 км/час, нижняя — 0 (мгновенно, она неподвижна относительно покрытия).
|
|
|
|
|
BISHA |
Re: Движени по окружности
|
||
08/01/09 |
Какую линейную скорость имеет верхняя точка обода велосипедного колеса, если велосипедист едет по горизонтальной дороге с постоянной скоростью 20 км/ч? 20 км/ч — если без проскальзывания. Линейная скорость по определению — расстояние деленное на время, а оно будет одинаковым.
|
||
|
|
|||
|
1rome1 |
Re: Движени по окружности
|
|
14/11/09 |
BISHA Ненене. Там ответ 40
|
|
|
|
|
Батороев |
Re: Движени по окружности
|
|
23/01/07 |
|
|
|
|
|
gris |
Re: Движени по окружности
|
||
13/08/08 |
Если прикрепить бумажку на обод, то в момент прохождения этой бумажки верхней точки своей траектории, она будет двигаться относительно земли со скоростью 40 км/ч. Если мы прикрепим к неподвижной части велосипеда бумажку рядом с верхней точкой обода, то она будет двигаться со скоростью 20 км/ч. У многих возникает недоумение по этому поводу. BISHA и имел в виду скорость «верхней точки обода» как некоторой виртуальной точки, не связанной ни к с одной материальной точкой. Типа солнечного зайчика.
|
||
|
|
|||
|
druggist |
Re: Движени по окружности
|
|
27/02/09 |
Типа солнечного зайчика. Который типа единственный, кто не линяет
|
|
|
|
|
BISHA |
Re: Движени по окружности
|
||
08/01/09 |
Там ответ 40 Вероятно, траектория точки обода циклоида, написать уравнение и взять производную.
|
||
|
|
|||
|
1rome1 |
Re: Движени по окружности
|
|
14/11/09 |
BISHA А на счет уравнения и производной поподробней…
|
|
|
|
|
Батороев |
Re: Движени по окружности
|
|
23/01/07 |
Можно еще представить гусеницу едущего танка, верхние траки довольно шустро перемещаются относительно деталей корпуса Все траки относительно корпуса имеют одинаковую скорость, но различную по направлению. Т.е. относительно корпуса — все шустрые! — Сб ноя 14, 2009 16:24:37 — Решил сделать небольшое добавление:
|
|
|
|
|
BISHA |
Re: Движени по окружности
|
||
08/01/09 |
|||
|
|
|||
|
druggist |
Re: Движени по окружности
|
|
27/02/09 |
Все траки относительно корпуса имеют одинаковую скорость, но различную по направлению. Т.е. относительно корпуса — все шустрые! Ну это какое-то буквоедство , а нижние траки относительно земли как раз покоятся
|
|
|
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
2020-03-27
Найдите скорость верхней точки пересечения двух катящихся колес (рис.а) в тот момент, когда она находится на одной горизонтали с центром большого колеса. Скорости колес одинаковы и равны $v$, радиусы колес $r$ и $R$.
Решение:
Вводим неизвестные: $v_{A}$ — скорость точки А и $gamma$ — угол, который она образует с горизонтом (рис.б). Скорость точки A образует угол $gamma$ с отрезком $O_{2}A$ и угол $(90^{ circ} + alpha — gamma )$ с отрезком $O_{1}A$, где $alpha = arccos frac{R-r}{r}$. Для этих двух отрезков наше уравнение принимает вид
$v_{A} cos gamma = v$,
$v_{A} cos (90^{ circ} + alpha — gamma ) = v cos (90^{ circ} — alpha )$.
Решение этой непростой системы уравнений мы оставляем читателям и приводим лишь окончательный ответ:
$v_{A} = v sqrt{1 + 4 tg^{2} alpha } = v sqrt{ frac{4r^{2} }{(R-r)^{2} } — 3 }$.
А нет ли более простого метода решения этой задачи? Оказывается, есть.
Метод, который мы предлагаем для решения задач со связями, заключается в переходе в движущуюся систему отсчета. Например, рассматривая движение жесткого стержня (см. рис.), мы можем «сесть на точку В», т.е. перейти в систему отсчета $K^{ prime}$, которая движется со скоростью $vec{v}_{0}$, равной скорости $vec{v}_{2}$ точки В. Выигрыш от такого перехода очевиден. Теперь точка В покоится относительно нас, и вместо двух движущихся точек осталась только одна точка А. Это большое упрощение.
Действительно, если точка В покоится, то единственным возможным движением стержня может быть только вращение относительно этой точки. При этом скорость $vec{v}_{1}^{ prime}$ точки A (относительно новой системы отсчета $K^{ prime}$) может быть любой по величине, но направлена она обязательно перпендикулярно стержню (рис.).
В неподвижной системе отсчета $K$, согласно классическому закону сложения скоростей, скорость точки A равна
$vec{v}_{1} = vec{v}_{1}^{ prime} + vec{v}_{0} = vec{v}_{1}^{ prime} + vec{v}_{2}$.
Давайте прочитаем эту формулу нужным для нас способом: «Да, скорости $vec{v}_{1}$ и $vec{v}_{2}$» концов стержня могут быть разными, но отличаются они лишь на вектор $vec{v}_{1}^{ prime}$, перпендикулярный самому стержню». А это означает, что проекции скоростей $vec{v}_{1}$ и $vec{v}_{2}$ на стержень одинаковы (проекция их разности $vec{v}_{1}^{ prime}$ на сам отрезок равна нулю). Наша волшебная формула подтверждена.
А теперь посмотрим, как с помощью этого метода можно проще решить задачу. Прежде подготовимся, чтобы не запутаться в обозначениях. Скорости центров колес, точек $O_{1}$ и $O_{2}$, одинаковы: $v_{1} = v_{2} = v$ и противоположно направлены: $vec{v}_{1} = — vec{v}_{2}$. Введем скорость $vec{v}_{0}$, равную по модулю $v$ и направленную влево. Эта скорость равна скорости большого колеса: $vec{v}_{2} = vec{v}_{0}$ и противоположна скорости малого колеса: $vec{v}_{1} = — vec{v}_{0}$.
«Сядем на большое колесо», т.е. перейдем в систему отсчета $K^{ prime}$, движущуюся со скоростью $vec{v}_{0}$ (рис.а). В этой системе отсчета большое колесо покоится, а малое движется вправо со скоростью $2v$. Нетрудно убедитьсяв том, что наш ответ для движущейся системы отсчета таков — скорость точки пересечения направлена вертикально вверх и равна
$v_{A}^{ prime} = 2v tg alpha$, где $alpha = arccos frac{R-r}{r}$.
Нам осталось лишь вернуться в лабораторную систему отсчета и с помощью классического закона сложения скоростей $vec{v}_{A} = vec{v}_{A}^{ prime} + vec{v}_{0}$ пересчитать скорость точки А. С помощью рисунка б получаем окончательный ответ:
$v_{A} = sqrt{v_{0}^{2} + v_{A}^{ 2 prime}} = v sqrt{1 + 4tg^{2} alpha} = v sqrt{ frac{4r^{2} }{(R-r)^{2} } — 3}$.
Решение закончено, ответ получен. Расплата за простоту -необходимость пересчитывать скорости при переходе из одной системы отсчета в другую. Впрочем, выбирайте сами, что для вас легче: решать непростую систему уравнений или разыскивать систему отсчета, в которой сразу можно указать направление неизвестной скорости.
Тип 5 № 290
i
Какую поступательную скорость имеют верхние точки обода велосипедного колеса, если велосипедист едет со скоростью 20 км/ч?
Спрятать решение
Решение.
Ответ: 40 км/ч.
Источник: Кирик Л. А. Самостоятельные и контрольные работы для 9 класса, Х.: «Гимназия», 2002 (№ 6 (дост.) стр. 43)
Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость
и модуль средней скорости
.
Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.
Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с
Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол
.
Скорость точек окружности
Решение:
Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра
м/с. Линейные скорости показаны для точек
оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки
скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга:
. В точке C скорости, напротив, сложатся, поскольку они сонаправлены:
м/с.
Определим теперь скорости точек и
. Понятно, что они будут равны численно, но направлены в разные стороны.
Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу
. Углы, которые образуются между векторами, показаны на рисунке, в том числе угол
. Тогда в параллелограмме
угол
, а так как
, то все углы в треугольнике равны
и он равносторонний, то есть
м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные
, точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.
Пробуксовывание
Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки
м/c, а верхней —
м/c.
Решение:
Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и
запишем отношения сходственных сторон:
Тогда
Тогда
Теперь обратимся к подобным треугольникам и
. Для них отношение сходственных сторон равно:
Откуда м/с.
Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и
, при этом не забываем о векторном сложении скоростей, берем скорость
со знаком «минус»:
м/с.
Ответ: 4 м/с.
Проскальзывание
Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки B
м/с. Определить скорость концов диаметра
, перпендикулярного к
, для того же момента времени. Под какими углами они направлены к горизонту?
Решение:
Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:
м/с.
Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса
и скорости поступательного движения центра колеса
, то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки
, данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек
и
равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:
Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как
Ответ: ,
Шарик катится по двум линейкам
Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно
см, и за время
с проходит
см. С какими скоростями движутся верхняя и нижняя точки шарика?
На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка
. Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника
. Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки
будет
Таким же способом определяем скорость верхней точки :
Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.
Задача 6. Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид:
, где
м,
м/с,
м/с
. Найти скорость автомобиля
, его тангенциальное
, нормальное
и полное
ускорения в момент времени
с.
Решение.
Путь:
Производная пути – линейная скорость:
Вторая производная – тангенциальное ускорение:
Нормальное ускорение:
Полное ускорение:
Задача7. Угол поворота диска радиусом см изменяется со временем по закону
. Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.
Решение: угловая скорость – производная угла:
Угловое ускорение – производная угловой скорости:
Линейная скорость:
Задача 8. Точка движется по окружности с постоянным угловым ускорением рад/
. Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.
Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.
Известно, что нормальное ускорение , тангенциальное ускорение
. При этом
, или
. Тогда
Искомый угол:
Ответ:
Два концентрических колеса
Задача 9. Два концентрических колеса радиусами см и
см вращаются с угловыми скоростями
рад/c и
рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.
Решение: определим радиус маленького (третьего) колеса, м:
Определим линейную скорость точек первого колеса:
Определим линейную скорость точек второго колеса:
Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:
Ответ: 20 рад/с
Задача 10. Гайку закручивают на болт за время . Длина болта
, резьба составляет угол
с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен
.
Скорость вращения гайки по ходу завинчивания на болт
Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (
). Тогда
.
Из рисунка видно, что
С другой стороны, так как длина болта , а гайка спускается по нему за время
, то
Тогда
И можно определить :
Тогда
Ответ:

 , то эпюра скоростей точек колеса строится в виде перевернутого прямоугольного треугольника с вершиной в нижней точке, вертикальным катетом
, то эпюра скоростей точек колеса строится в виде перевернутого прямоугольного треугольника с вершиной в нижней точке, вертикальным катетом  и верхним катетом
и верхним катетом  (соответственно, в центре колеса — средняя линия треугольника равна
(соответственно, в центре колеса — средняя линия треугольника равна 







