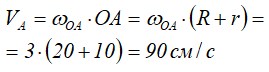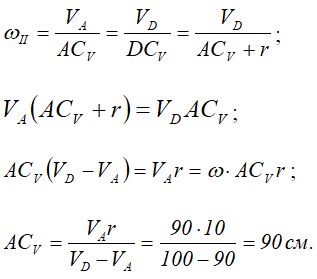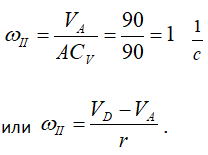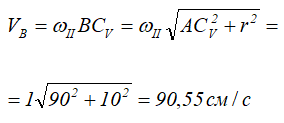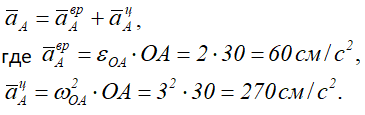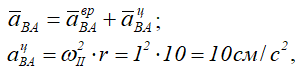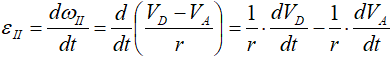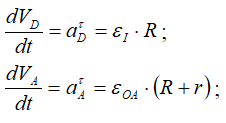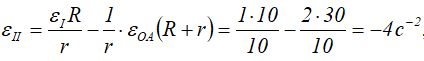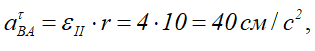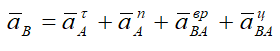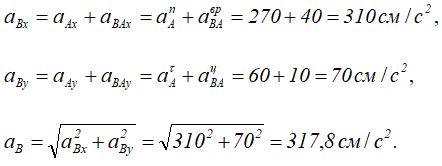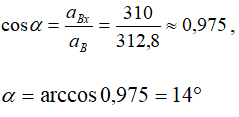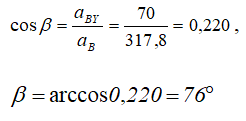Как найти скорость вращения точек колеса

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Кинематика колеса.

Движение
колеса имеет сложную структуру. Колесо
перекатывается по поверхности дороги
теоретически без проскальзывания, в то
время как в действительности проскальзывание
существует, но составляет сравнительно
небольшую величину.

Введём
три системы координат: xy – неподвижную
относительно поверхности дороги; x1y1
– подвижную относительно поверхности
дороги; x1y1
– подвижную и связанную с рамой велосипеда
или осью колеса, x2y2
– подвижную и связанную непосредственно
с колесом, которая, таким образом,
совершает сложное движение. Система
координат x1y1
совершает переносное поступательное
движение, в котором все точки имеют
одинаковую скорость V.
Система координат x2y2
совершает относительное вращательное
движение, в котором каждая точка колеса
движется с окружной скоростью Vp
= wp,
где w
– угловая скорость относительного
движения; p
– расстояние от начала координат O1
до рассматриваемой точки. Векторная
сумма переносной и относительной
скоростей любой точки колеса равна
абсолютной скорости Va=V+Vp

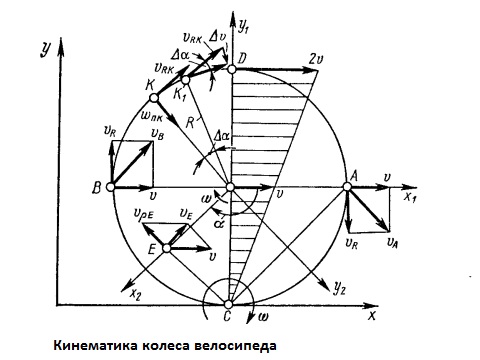
Точка
C
является точкой касания колеса с
поверхностью дороги и является неподвижной
при принятом выше условии – отсутствии
проскальзывания колеса относительно
дороги и деформации однотрубки. Скорость
точки С, принадлежащей колесу (p=R),
равна

Для
произвольной точки E
колеса, находящейся на расстоянии p=O1E
от оси колеса, скорость определится как
векторная сумма Ve=V+VpE.
Численное значение скорости точки E
может быть определено с помощью выражения

С
другой стороны, плоскопараллельное
движение колеса в каждый момент времени
можно представить как вращение около
мгновенного центра вращения. В данном
случае мгновенным центром вращения
является мгновенный центр скоростей в
точке C,
в котором скорость равна нулю. Положение
мгновенного центра скоростей можно
определить также как точку пересечения
перпендикуляров к направлениям векторов
абсолютных скоростей двух произвольных
точек колеса, например А и Е.

Тогда
скорость любой точки колеса определяется
выражением V=wp,
где W
– угловая скорость вращения колеса
вокруг мгновенного центра скоростей,
равная угловой скорости вращения колеса
вокруг своей оси O1;
p
– расстояние от рассматриваемой точки
до мгновенного центра вращения. Так,
для точки D
это расстояние составляет Pd=2R,
для точек A
и B
будет Pв=Pа=Rsqrt2;
для произвольной точки Е

Направлен
вектор абсолютной скорости в сторону
вращения перпендикулярно к соответствующему
отрезку P,
соединяющему мгновенный центр скоростей
с рассматриваемой точкой.

Окружная
скорость любой i-й
точки Vri
направлена по касательной к траектории
её движения относительно оси вращения
колеса O1.
По мере увеличения угла “a”
точка A
последовательно занимает положения C,
B
и D,
а вектор Vri,
оставаясь постоянным по величине, меняет
своё направление. Это объясняется
наличием нормального ускорения движения
даже при равномерном вращении колеса,
т.е. при тангенциальном ускорении, равном
нулю. При бесконечно малом угле поворота
delta(a),
на который колесо поворачивается за
бесконечно малый промежуток времени
delta(t),
скорости в точках K
и K1
представляют собой равные по величине
векторы Vrk
и Vrk1,
касательные к окружности в этих точках.
Перенеся вектор скорости Vrk
в точку K1
получим вектор delta(V),
представляющий собой изменение скорости
точки K
при переходе в положение K1
за время delta(t).
Из подобия треугольников и с учётом
того, что delta(t)->0,
можно записать

Отсюда
следует, что нормальное ускорение точки
K

Это
ускорение направлено к центру колеса
и называется центростремительным. В
случае неравномерного движения полное
ускорение складывается из нормального
и тангенциального, которые взаимно
перпендикулярны:

Кинетостатика
системы

При
движении велогонщик и велосипед образуют
единую движущуюся систему, в которой
силы взаимодействия являются внутренними
и сами по себе не могут обеспечить
движения общего центра масс системы.
Для движения необходимы внешние силы,
которые в данном случае сводятся к силам
тяжести, силам трения колёс о дорожное
покрытие и силам аэродинамического
сопротивления.

Для
начала рассмотрим отдельно взятые
ведущее и ведомое колёса велосипеда, а
затем систему гонщик-велосипед в целом.

Ведущее
колесо.

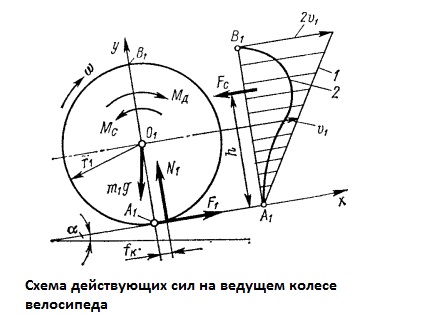
К
ведущему колесу массой m1
с моментом инерции J1
приложен движущий момент Mд,
под действием которого со стороны дороги
возникает сила трения скольжения F1=fN1,
где N1
– сила нормального давления; f
– коэффициент трения скольжения. Точка
A1
является мгновенным центром вращения
и её скорость равна нулю. Поэтому f
есть коэффициент трения покоя, величина
которого неопределенна и может принимать
значения от 0 до fmax.
Эпюра скоростей 1 в диаметральном сечении
колеса A1B1
является фактически эпюрой скоростей
набегающего воздушного потока, сила
сопротивления которого Fe,
приложенная в центре масс эпюры 2
суммарного лобового и вихревого
сопротивлений, создаёт момент полного
аэродинамического сопротивления Мe.

Колесо,
имеющее пневматическую шину в виде
однотрубки, деформируется в зоне контакта
с поверхностью дороги, что приводит к
смещению реакции N1
на некоторую величину fк,
называемую коэффициентом трения качения
Mк1=fкN1.
Учитывая малось величины fк,
в дальнейшем будем считать реакцию N1
приложенной в точке A1.

Уравнения
движения колеса запишутся в виде системы:

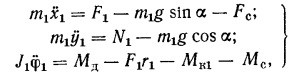
Где
x1,
y1
– координаты положения оси колеса O1;
Ф1 – угол поворота ведущего (заднего)
колеса; “a”
– угол наклона поверхности дороги к
горизонтали.

Если
колесо катится без проскальзывания, то
x1=r1Ф1;
y1=0;
N1=m1g*cos”a”.
Сила трения F1
без учёта
сил аэродинамического сопротивления

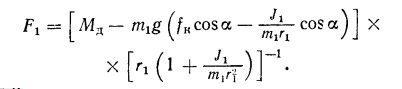
Движущий
момент Mд
в правой части уравнения может принимать
различные значения, но если правая часть
уравнения станет больше, чем fmax
N1,
то появится проскальзывание колеса
относительно дороги и увеличение Mд
оказывается нецелесообразным. Максимальное
ускорение составляет величину

Характерно,
что под уклон (“a”<0)
можно обеспечить движение без
проскальзывания с большими ускорениями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример решения задачи по определению величины и направления полной скорости и полного ускорения при сложном движении точки колеса кривошипа.

Теория по теме

Задача

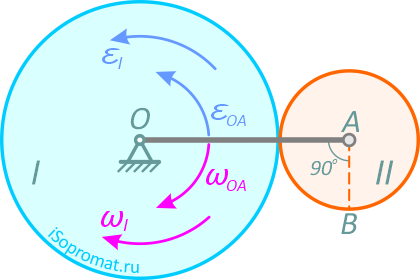
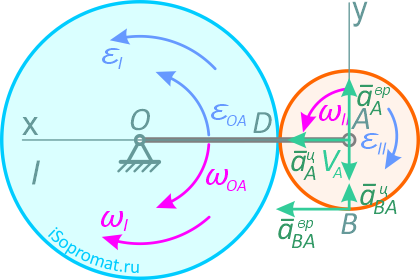
Колесо I с радиусом R вращается вокруг оси, проходящей через центр колеса перпендикулярно плоскости чертежа с угловой скоростью ω_I и угловым ускорением ε_I.

Рис. 2.7

Независимо от него на той же оси вращается кривошип ОА с угловой скоростью ω_OA и угловым ускорением ε_OA. Кривошип приводит в движение колесо II с радиусом r, которое катится по колесу I (рис. 2.7).

Найти скорость V_B и ускорение a_B точки B, если R=20 см, r=10 см, ω_I=5 с^-1, ε_I=1 с^-2, ω_OA=3 с^-1, ε_OA=2 с^-2.

Другие примеры решений >
Помощь с решением задач >

Решение

Колесо I и кривошип совершают вращательное движение, а колесо II – плоскопараллельное движение.

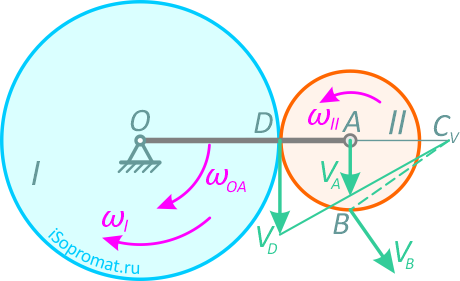
Найдем скорость точки В, для этого определим положение мгновенного центра скоростей колеса II. Чтобы найти МЦС нужно, знать направление скоростей хотя бы двух точек тела.

Найдем скорость точки А, которая принадлежит колесу II и кривошипу ОА.

Вектор V_A направлен перпендикулярно отрезку ОА в сторону вращения кривошипа (рис. 2.8).

Рис. 2.8

В точке соприкосновения колес скорость точки колеса II должна равняться скорости точки колеса I. Обозначим эту точку буквой D. Эта точка не принадлежит кривошипу ОА. Так как движение колеса I известно, можно найти скорость точки D.

Вектор скорости точки D направлен перпендикулярно радиусу OD в сторону вращения колеса I. Таким образом, нам известны скорости двух точек колеса II. Проведем перпендикуляр к скоростям в точках А и D и прямую, проходящую через концы векторов скоростей V_D и V_A.

В точке пересечения этих линий и будет МЦС для колеса II. Обозначим его буквой C_V.

Найдем расстояние AC_V:

Тогда

Зная угловую скорость колеса II и его МЦС, найдем скорость точки В.

Вектор V_B направлен перпендикулярно отрезку ВС_V в сторону вращения колеса II.

Определим ускорение точки В.

Согласно теореме, ускорение точки В определятся по формуле

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг
полюса А.

Точка А принадлежит кривошипу ОА – движение которого известно, тогда

Вектор a^τ_A — направлен перпендикулярно ОА, в сторону, обратную V_A, т.к. вращение кривошипа по условию задачи замедленное.

Рис. 2.9

Вектор aⁿ_A — направлен от А к О.

Вектор

и направлен от точки В к полюсу А.

Для его вычисления найдем угловое ускорение ε_II:

r – в задачах такого типа величина постоянная, выносится за знак производной:

Отсюда

Знак «-» говорит о том, что колесо II вращается замедленно.

Величина

и направлена перпендикулярно aⁿ_BA. Полное ускорение найдем, сложив все слагаемые:

Направив ось АX вдоль АО, ось АY перпендикулярно АО, получим:

Вектор a_B составляет с осью АХ угол α, косинус
которого

а с осью AY угол β, косинус которого:

Другие примеры решения задач >

Условие задачи:

Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает 309 оборотов в минуту.

Задача №1.8.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(D=1,1) м, (nu=309) об/мин, (upsilon-?)

Решение задачи:

Строго говоря, относительно Земли точки колеса при движении автомобиля совершают сложное движение, при котором они двигаются и поступательно, и вращательно. Но если перейти в систему отсчета (СО), связанную с автомобилем, то колеса будут уже совершать простое вращательное движение. При этом понятно, что линейная скорость крайних точек колеса равна скорости движения автомобиля (upsilon).

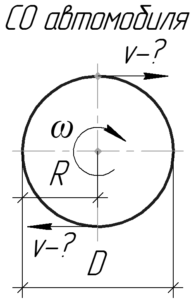
Эту линейную скорость можно определить по такой формуле, учитывая, что радиус равен одной второй диаметра:

[upsilon  = omega R = frac{{omega D}}{2};;;;(1)]

Угловую скорость (omega) найдем, используя частоту вращения (nu), данную в условии, по такому выражению:

[omega  = 2pi nu ;;;;(2)]

Подставим (2) в (1):

[upsilon  = frac{{2pi nu D}}{2} = pi nu D]

Перед тем, как подставлять значения и вычислять ответ, переведем частоту вращения в систему СИ.

[309; [1/мин] = frac{{309}}{{60}}; [1/с] = frac{{103}}{{20}}; [1/с]]

[upsilon  = 3,14 cdot frac{{103}}{{20}} cdot 1,1 = 17,79; м/с]

Ответ: 17,79 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.4 С какой скоростью едет велосипедист, если колесо делает 100 об/мин. Радиус
1.8.5 Угол поворота колеса радиусом 0,2 м изменяется по закону phi=9,42t (рад)

Enter the rotations per minute (RPM) of the axle and the wheel diameter into the calculator to determine the wheel speed. This calculator can also evaluate the diameter or RPM when provided the other variables.

• Bike Speed Calculator
• Gear Inch Calculator
• Rev Per Mile Calculator
• Wheel Horsepower Calculator

Wheel Speed Formula

The following formula is used to calculate a wheel speed.

S = [2*PI*(D/2)] * [ RPM/60 ]

• Where S is the wheel speed
• RPM is the rotations per minute
• D is the diameter

To calculate wheel speed, multiply half the diameter by 2 times pi, then multiply again by the RPM over 60.

Wheel Speed Definition

What is wheel speed? Wheel speed commonly refers to the instantaneous tangential velocity of a wheel at a specific diameter that is rotating at a constant RPM.

Example Problem

FAQ

Does wheel size affect speed? Wheel size will change the speed of a vehicle if the RPM of the wheel stays constant. Increasing the wheel size will increase the speed when RPM is constant, and decreasing the wheel size will decrease the speed when RPM is constant. In the real world, keeping a constant RPM with a larger wheel requires more torque.