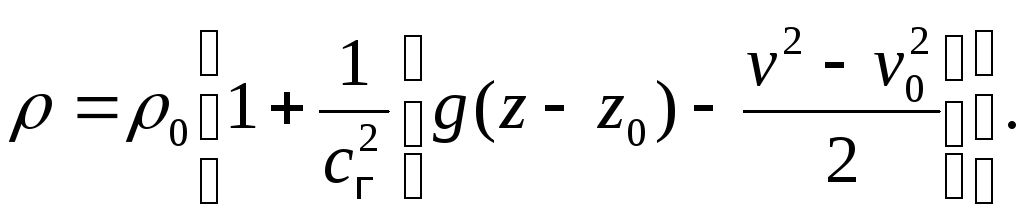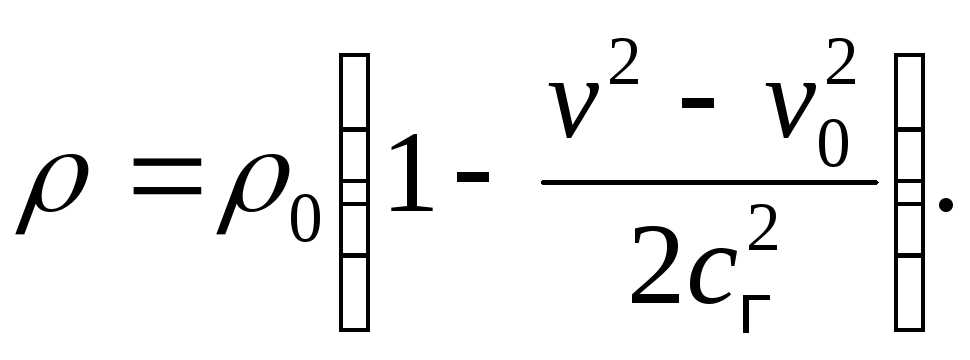Как найти скорость звука в газе - Исправление недочетов и поиск решений вместе с Examum.ru

Зависимость
плотности от давления ярко проявляется
у газов: при увеличении давления на газ
его плотность увеличивается. Кроме
того, газ при сжатии нагревается.
Теплопроводность у газа мала, поэтому
тепло не успевает уходить из нагретых
областей. Это значит, что для газа сжатие
является адиабатным
процессом (т.е. без передачи тепла).
Адиабатный процесс для идеального газа
описывается уравнением

(а)

в котором константа
называетсяпоказателем
адиабаты,

При сжатии масса
не меняется. Пусть
– масса газа и его объём. ТогдаПодставив в (а), получимили

(2.12)

где
Получили связь междуи

Из (2.12) находим

(2.13)

Из (2.12) следует

(2.14)

Подставим в (2.13):

Отсюда
Подставив в (2.11), будем иметь

(2.15)

Получилась
формула определения скорости звука в
газе.

2.9. Решение уравнения Эйлера для газа и сжимаемой жидкости

Воспользуемся
равенством (2.9), в котором не использовалось
условие несжимаемости. Подставим (2.13)
в (2.9). Получим

(а)

Пусть при
выполняются условия:(б)

Подставим их в
(а):

Вычтем это выражение
из (а):

Отсюда

(в)

Найдём чтобы сюда вставить. Из (2.14) и (2.15) имеем
ОтсюдаПодставим в (в):

(г)

Заметим, что величина
очень мала (т.к.близко к нулю, а скорость звукавелика). Кроме того, скорость течения
обычно мала по сравнению сперепад высотневелик. Поэтому в фигурных скобках
второй член мал и выражение (г) допускает
следующее приближение:

В частности, для
горизонтального канала (когда будем иметь

Глава 3 динамика вязкой жидкости

3.1. Понятие о вязкости

Реальная жидкость
и газ имеют вязкость.

Вязкость
– это сила трения между слоями текущей
жидкости.

Именно из-за
вязкости текущая жидкость, предоставленная
самой себе (т.е. когда убраны причины,
вызвавшие движение), останавливается.

Рассмотрим два
опыта, в которых проявляется внутреннее
трение (вязкость).

О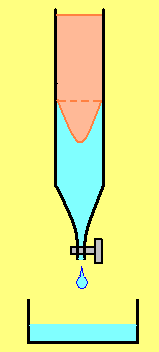п ы т 1. В вертикальную трубку с краном
внизу нальём воду, а на неё сверху
осторожно дольём коричневое растительное
масло (рис. 3.1). В состоянии равновесия
граница раздела будет горизонтальной
(пунктирная линия).

Откроем кран так,
чтобы течение было очень медленным.
Вскоре граница раздела примет форму
параболоида вращения. Слой жидкости,
прилегающий к стенке трубки, неподвижен.
Скорость течения остальных слоёв
увеличивается по мере приближения к
оси трубки.

О п ы т 2. Поместим
в жидкость две параллельные пластины
одинаковой площади
расстояние между которымипричём(рис. 3.2).

Будем перемещать
вправо верхнюю пластину Рис.
3.1

со скоростью
Убеждаемся, что для перемеще-

ния пластины с
постоянной скоростью, к ней нужно
приложить определённую постоянную силу
Раз пластина движется не ускоренно,
значит, на неё действует нулевая
суммарная сила. Следовательно, внешнюю
силукоторую мы прикладываем, уравновешивает
противоположно направленная сила трения
жидкости о пластину. Обозначим её

Выполняя этот опыт
при различных
(как это делал Ньютон), можно убедиться,
что

Рис.
3.2

Значит,

(3.1)

Коэффициент
называетсядинамической
вязкостью;
он зависит от типа жидкости и её состояния
(например, от температуры). Опыт показывает,
что при нагревании вязкость жидкости
уменьшается, а газов – растёт.

Относительно
верхней пластины нижняя пластина
движется с той же скоростью
но в обратную сторону, влево. Значит, на
нижнюю пластину действует сила

Формула (3.1)
определяет не только силу трения,
действующую на пластину, но и силу трения
между соприкасающимися слоями жидкости.

Для слоёв, находящихся
на расстоянии
скорости отличаются наПоэтому формулу (3.1) можно записать так:

(3.2)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Скорость звука в газах, формула

Если:
c — Скорость звука в газе (м/с),
χ = с_p / с_u — показатель адиабаты,
ρ — Плотность газа (кг/м³),
p — Давление газа (Н/м²),
R — Газовая постоянная (Дж/кг·К),
T — Температура газа (К),
То, Скорость звука в газах описывается следующей формулой:

[ c = sqrt{frac{χp}{ρ}} = sqrt{χRT} ]

Скорость звука в газах в широких пределах зависит только от температуры и не зависит от давления газа.

Вычислить, найти скорость звука в газах по формуле (1)

Для примера, в полях ввода данные для воздуха.

Скорость звука в газах	стр. 582

Источник

Лабораторная работа № 6

Определение по скорости звука в газе.

Цель
работы: Экспериментальное определение показателя
адиабаты

по измерениям скорости звука в воздухе.

Принадлежности: Звуковой
генератор ГЗ – 102; электронный осциллограф С1 – 72; микрофон; телефон.

Литература:

1. Матвеев А.Н. Молекулярная физика. М., высшая школа,
1987.

2. Сивухин Д.В. общий курс физики, т.2, 1976, с.552.

3. Кикоин А.К., Кикоин И.К. Молекулярная физика. М., Наука,
1976.

Краткая теория

Один из способов определения адиабаты в газах
основан на измерении скорости звука. Скорость упругих продольных волн в упругой
среде определяется формулой:

где модуль Юнга, — коэффициент упругости.

Эта формула пригодна также для жидкостей и газов.
Коэффициент упругости для газов определяется по аналогии с твердым телом. Закон
Гука устанавливает зависимость между
относительным удлинением и напряжением .

Если мы имеем столб газа в цилиндре под поршнем,
то под действием силы на поршень газ сжимается и высота уменьшается на Δ. В этом случае =
DР
– приращение давления, =

Следовательно, =

Знак “–” говорит о том, что приращение объема ΔV
и ΔР имеют разные знаки.

Переходим к дифференциалам:

Величина зависит
от характера процесса сжатия газа. В звуковой волне сжатия и расширения газа
следуют так быстро друг за другом, сто смежные участки среды не успевают
обмениваться теплом, и процесс можно считать адиабатическим.

Из уравнения адиабаты =const
можно получить, продифференцировав его:

Отсюда ;

Следовательно, коэффициент упругости

Тогда

может показаться, что зависит
от Р, но это не так, с увеличением Р увеличивается ρ, а =
const.

Используя уравнение Клапейрона-Менделеева, найдем:

=
(1)

т.е. скорость звука в газах можно определить по формуле (1),

где R – газовая
постоянная, Т – температура газа в Кельвинах, μ – его молярный вес. Преобразуя
эту формулу, найдем:

(2)

Таким образом для определения показателя адиабаты
достаточно измерить температуру газа и скорость распространения звука (молекулярный
вес газа предполагается известным). Для измерения скорости звука служит
установка, изображенная на рис.1.

Звуковые колебания в трубе возбуждаются телефоном
Т. Колебания улавливаются микрофоном М.
Мембрана телефона приводится в движение переменным током звуковой частоты, в
качестве источника переменной э. д. с. используется звуковой генератор ГЗ –
102. Возникающий в микрофоне сигнал наблюдается на осциллографе С1-72.

Звуковая волна, распространяющаяся вдоль трубы,
испытывает многократные отражения от торцов. Звуковые колебания в трубе являются
наложением всех отраженных волн и , вообще говоря, очень сложны. Картина резко
упрощается, если длина трубы равна целому числу полуволн, т. е. когда

(3)

где λ – длина волны звука в трубе, а n – любое целое число.

Если условие (3) выполнено, то волна, отраженная
от заднего торца трубы, вернувшаяся к ее началу и вновь отраженная совпадает
по фазе с падающей.

Аналогичным образом совпадает по фазе волны,
движущиеся от заднего торца к переднему после первого отражения от заднего
торца, после второго отражения и после всех последующих отражений. Совпадающие
по фазе волны усиливают друг друга. амплитуда звуковых колебаний при этом резко
возрастает – наступает резонанс.

Скорость звука v
связана с его частотой f и длиной волны λ
соотношением

(4)

Подбор условий, при которых возникает резонанс, можно
производить следующим образом: при неизменной частоте звукового генератора (а
следовательно, и длине звуковой волны) можно изменять длину трубы. Для этого в
работе применяется труба с подвижным телефоном. Расстояние между телефоном и
микрофоном постепенно увеличивается и наблюдается ряд последовательных
резонансов. Возникновение резонансов легко наблюдать на осциллографе по
резкому увеличению амплитуды колебаний. Для последовательных резонансов имеем:

(5)

Из (4) и (5)
имеем:

(6)

Описание экспериментальной установки

Экспериментальная установка для определения скорости звука
в воздухе (газе) двумя методами представлена на рис. 1.
Установка включает в себя следующие узлы и приборы:

Рис. 1
Установка для экспериментального определения показателя адиабаты в газе.

1. звуковой генератор ГЗ – 102 2. Труба с подвижным
телефоном

3. Микрофон 4. Телефон 5. Осциллограф С1 – 72

1. Звуковой генератор ГЗ – 102 генерирует
электрические колебания звуковой частоты (20 – 2000 Гц) и питает телефон,
который преобразует их в механические колебания мембраны. Последняя является
источником звуковых волн.

2. Труба с подвижным телефоном представляет собой
пластмассовую трубу с прорезью. С одного торца этой трубы неподвижно установлен
микрофон, а в трубе, как поршень в цилиндре свободно перемещается телефон.
Таким образом, расстояние между телефоном микрофоном можно менять.

3. Микрофон преобразует механические колебания
частиц среды (воздуха) в электрические.

4. Электронный осциллограф служит для наблюдения
электрических колебаний, регистрируемых микрофоном.

Измерения

1. Ознакомьтесь с установкой, выяснив назначение каждой
ручки и тумблера.

2. Установите переключатели осциллографа С1 – 72 в
следующее положения:

Вольт/делен. – 0,2

Время/делен – 2ms

Включите осциллограф в сеть и дайте ему прогреться 5 – 7
минут. На экране должна появиться горизонтальная линия, прочерченная электронным
лучом.

3. Включите звуковой генератор ГЗ – 102. Подберите
напряжение на выходе генератора так, чтобы на осциллографе наблюдались
колебания, достаточной амплитуды. Остановите картину на осциллографе, изменяя
частоту развертки. Убедитесь в том, что колебания имеют неискаженную
синусоидальную форму. Если форма колебаний искажена, уменьшайте амплитуду
сигнала, поступающего с генератора, пока искажения не прекратятся.

4. Измерьте скорость звука на различных частотах:

а) Исходя из примерного значения скорости звука
(300 м/с), рассчитайте, в каком диапазоне частот следует вести измерения, чтобы
при удалении телефона от микрофона можно было наблюдать 4 – 7 резонансов.

б) Установите на звуковом генераторе минимальную
из рассчитанных частот и , плавно изменяя расстояние между телефоном и микрофоном,
последовательно пройдите все доступные для наблюдения точки резонанса. Момент
резонанса фиксируйте по максимальному значению амплитуды колебания на экране
осциллографа. Для каждого случая резонанса запишите номер резонанса и
соответствующую ему координату телефона. Проведите такие измерения сначала
увеличивая расстояние между телефоном и микрофоном, а затем уменьшая его.

Повторите измерения при других частотах ( всего 4
– 6 различных значений частоты).

в) Полученные результаты для каждой частоты
изобразите на графике, откладывая по оси абсцисс номер очередного резонанса, а
по оси ординат – координату телефона. Через точки проведите наилучшую прямую и
по тангенсу угла наклона определите длину полуволны.

г) По графику оцените ошибку измерения .

Вычислите значение скорости звука и оцените
точность полученного результата (ошибка в градуировке шкалы частот генератора
не превосходит половины минимального деления шкалы).

Сопоставьте значения скорости звука, измеренные
на различных частотах. Проверьте находятся ли эти значения в согласии друг с другом.

Найдите среднее значение скорости звука,
используя все результаты измерений.

По формуле (2) вычислите
значение γ и оцените ошибку.

Контрольные вопросы

1. Какому
термодинамическому процессу соответствует процесс распространения звука в
среде? Запишите уравнение этого процесса. Чему равна теплоемкость этого
процесса?

2.
Получите уравнение адиабатического
процесса исходя из математической формулировки первого начала.

3. Получите
уравнение политропического процесса. При каких условиях политропический процесс
переходит в адиабатический, изотермический, изобарический, изохорический
процессы?

4. Получите
выражения для работы, совершаемой системой при этих процессах.

5. Запишите
математическое выражение первого начала термодинамики. Какие величины, входящие
в это уравнение являются функциями состояния и какие – функциями процесса?
Почему?

6. Почему первый
закон термодинамики эквивалентен утверждению о невозможности построения вечного
двигателя первого рода?

7. Ограничены ли
каким-нибудь пределами возможные значения теплоемкости?

8. При каких условиях
теплоемкость может иметь отрицательный знак? Возможен ли такой случай?

9. Рассматривая
воздух как двухатомный идеальный газ, выясните как зависит отношение от температуры? Скажется ли это или нет
на скорости распространения звука в воздухе?

10. Зависит ли скорость
распространения звука в воздухе от его влажности? Ответ обосновать.

11. Вывести рабочую формулу,
связывающую скорость звука с показателем адиабаты.

12. Как в опыте осуществляется
подбор условий, при которых в трубе возникает резонанс?

13. Дайте определение длины
волны. Как она определяется из опыта?

14.
Сравните экспериментально полученные
значения скорости звука и показателя адиабаты с теоретическими данными. В чем
Вы видите причину расхождения?

Источник

Прочность полученных бетонов не зависела от способа получения фосфата алюминия. Однако, водостойкость бетона с использованием A№O4, полученного вторым способом, была заметно выше.

Использование фосфата алюминия вместо гексафторсиликата натрия позволяет производить экологически безопасные строительные материалы.

Литература

1. Способ получения геля алюминия. Патент РФ № 2149138. 2000.

2. Субботкин М. И. Курицина Ю. С. Кислотоупорные бетоны и растворы. М., 1967.

3. Тихонов В. Н. Аналитическая химия алюминия. М. : Наука, 1971.

4. Шарло Г. Методы аналитической химии. Л. : Химия, 1965.

V. N. Volkov, M. L. Davtyan

SYNTHESIS AND APPLICATION OF ALUMINUM PHOSPHATE IN THE PRODUCTION OF ACID-PROOF CONCRETES

Synthesis of aluminum phosphate was carried out with the help of two methods. The chemical composition of the test samples was defined with the help of gravimetric and photometric methods. The synthesized salts wereexamined in the preliminary test as an initiator of the solidification of the acid-proof concretes consisted of liquid glass. The optimal mass correlation between the constituents of the dry mix, liquid glass and aluminum phosphate was identified.

Keywords: synthesis, aluminum phosphate, chemical composition, initiator, acid-proof concretes.

Волков Владимир Николаевич — доцент кафедры «Химия» ФГБОУ ВПО ПсковГУ, канд. хим. наук, доцент.

Давтян Мкртыч Левонович — доцент кафедры «Инженерная защита окружающей среды» ФГБОУ ВПО ПсковГУ, канд. хим. наук, доцент.

УДК 534.22

С. С. Воронков

О СКОРОСТИ ЗВУКА В ГАЗАХ

Рассмотрены различные формулы для скорости звука в газах. Отмечается, что в потоке вязкого теплопроводного газа с поперечным сдвигом необходимо учитывать влияние диссипации энергии и теплообмена на скорость звука при анализе возникновения турбулентности.

Ключевые слова: скорость звука, вязкий теплопроводный газ, возникновение турбулентности.

В общем случае под скоростью звука понимают местную скорость распространения малых возмущений относительно движущегося газа в данной точке потока и определяют её по формуле (Лойцянский, 1979).

др

а = —, др

(1)

где а — скорость звука, р и р — давление и плотность газа.

Первые теоретические исследования по определению скорости звука в воздухе принадлежат И. Ньютону (1989). Ньютон считал, что процесс распространения звука происходит изотермически. Давление и плотность в этом случае связаны между собой уравнением Бойля-Мариотта

Тогда, вычисляя производную по формуле (1), для изотермической скорости звука получим

Формула для изотермической скорости звука (3) носит название формулы Ньютона. Однако найденные по формуле (3) значения скорости звука были примерно на 20 % меньше значений, полученных опытным путём.

Причину расхождений установил П. Лаплас (Рэлей, 1955), который показал, что совпадение теории с экспериментом значительно улучшается, если процесс распространения считать адиабатным и изоэнтропным. В качестве уравнения состояния необходимо использовать уравнение адиабаты

где к — показатель адиабаты.

Тогда, вычисляя производную по формуле (1), для адиабатной и изоэн-тропной скорости звука получим

Формула (5) получила название формулы Лапласа. Значения скорости звука, вычисленные по формуле (5), практически совпадают с опытными данными.

Дальнейшие исследования влияния различных факторов (вязкости, теплопроводности и др.) на скорость звука в газах были выполнены в работах Стокса, Кирхгофа, Гельмгольца, Рэлея и других (Рэлей, 1955). Общим выводом этих работ является следующее: при распространении звука в открытом пространстве в виде плоских волн процесс распространения является адиабатным, и в первом приближении трение в газе не влияет на скорость звука. Лишь в очень узких трубах вязкость и теплопроводность воздуха оказывают заметное влияние на скорость распространения. Эти результаты, полученные для покоящейся среды, хорошо согласуются с экспериментальными данными и являются

Р = сош1.

(2)

(3)

— = сош1. рк

(4)

(5)

в настоящее время классическими. Но они, как было отмечено, получены для покоящейся среды и необоснованно экстраполируются на область движущегося газа. В потоке вязкого газа с поперечным сдвигом возникает интенсивная диссипация энергии, и предположения об изоэнтропности и адиабатности процесса при определении скорости звука требуют проверки.

В работе Воронкова С. С. (2004) получена формула для скорости звука в вязком теплопроводном совершенном газе, учитывающая диссипацию энергии и теплообмен

а =

Ф=ЦлдГ

дx I дx

V • (a2gradр — gradp) + (к -1) Ф др дt

д_( ЛдГ’] + д ( л дГ ду

(6)

л—1 +—I л— дуу & V д2

+ Ц

( ди (ду» 2 ‘ дм V (

1дх г у +( + V

(дм ду у+ (ди дм V

кдУ + д2 Г дх )

ду ди дх ду

(ди ду дw

+ — + —

дх ду д2

где а5— адиабатная и изоэнтропная скорость звука; Ф — функция, учитывающая диссипацию энергии и теплообмен; Т — температура газа; V — вектор скорости газа с проекциями и, V, w на оси декартовой системы координат х, у, ъ соответственно; Л — коэффициент теплопроводности; ц — коэффициент динамической вязкости; t — время.

Формула (6), найденная в работе (Воронков, 2004), получила название формулы Воронкова. При выводе формулы (6) не делались никакие предположения о характере процесса распространения возмущения. Поэтому для совершенного газа формула (6) является наиболее общей и учитывает диссипацию энергии и теплообмен в потоке.

Отличие формулы (6) от формулы Лапласа (5) состоит в наличии дополнительного члена, учитывающего диссипацию энергии и теплообмен. Возникает вопрос о значимости этого члена в различных условиях. В работе (Воронков, 2005) проведена оценка этого члена для плоской звуковой волны, распространяющейся в покоящемся вязком теплопроводном газе. Скорость звука в этих условиях, с привлечением формулы (6), найдется

а =

2л(к — 1)и

* ( 4

Лр 0

(

—ц + Л

1 1

С08

(<< — пх) ,

(7)

при возмущении скорости и ‘ = и*8т( ш t — пх); где и* — амплитуда возмущения скорости, ш — круговая частота возмущения, п — волновое число,

п = 2л/Л, Л — длина волны, л = 3,14….; р0 — плотность покоящегося газа; с„,ср — удельные изохорная и изобарная теплоёмкости.

Оценим величину второго члена под корнем при уровне звукового давления 70 дБ и частоте акустического возмущения 1000 Гц. Амплитуда возмущения скорости для воздуха при этих значениях равна и* = 2 • 10-4 м/с. Величина второго члена под корнем равна 4 • 10-8. Адиабатная скорость звука для воздуха при 20 °С равна 343 м/с. Таким образом, при вычислении скорости звука в покоящемся вязком теплопроводном воздухе вторым членом в формуле (7) можно пренебречь как величиной второго прядка малости. Этот вывод совпадает с результатами, полученными Стоксом, Кирхгофом, Гельмгольцем, Рэлеем (Рэлей, 1955).

Ситуация меняется при распространении звука в потоке вязкого газа с поперечным сдвигом. В потоке возникает интенсивная диссипация энергии и при вычислении скорости звука необходимо использовать формулу (6), учитывающую диссипацию энергии и теплообмен.

При рассмотрении распространения звука в потоке вязкого газа принцип суперпозиции не применим, так как уравнения, описывающие эти процессы, нелинейные и будет происходить взаимодействие основного потока с акустическим полем. Поэтому использовать полученную формулу (6) для определения скорости звука без знания характеристик потока вязкого газа не представляется возможным. Для нахождения скорости звука с учётом диссипации энергии и теплообмена в работе (Воронков, 2004) была составлена математическая модель, включающая уравнения неразрывности, Навье-Стокса, энергии и состояния. Численное решение системы дифференциальных уравнений в частных производных осуществлялось по двухшаговой схеме Браиловской (Роуч, 1980). Моделировался процесс распространения акустических возмущений в потоке вязкого газа в плоском канале. В качестве начальных условий задавалось стационарное ламинарное течение с параболическим распределением скоростей. Акустическое возмущение задавалось на входе в канал в виде гармонического сигнала с амплитудой возмущения плотности Ар. Скорость звука определялась по формуле

а = 1— = <1^—!-, (8)

1Др р1 -р

где р1, р1, р, р — значения давления и плотности на разных временных слоях в фиксированной точке канала.

Расчёты проводились в плоском канале. Количество узлов по оси х (вдоль канала) принималось і=51, количество узлов по оси у (поперек канала) j = 11. Шаг по пространственной переменной Дх = Ду = 10-2 м. Шаг по времени Д1 = 2 х 10-5 с. Амплитуда возмущения плотности варьировалась в пределах Др = 10-10… 10-11 кг/м3. Частота звука принималась (основной режим) 1000 Гц. Максимальная скорость потока на оси канала принималась (основной режим) итах = 0,1 м/с.

На рисунке 1 приведен характерный закон изменения скорости звука в фиксированный момент времени вдоль канала в плоскости j = 6. Приведены изо-энтропная скорость звука авт6і 59 и скорость звука с учётом диссипации энергии

и теплообмена арпб159. Изоэнтропное значение скорости звука аБтб 59 практически постоянно — около 343,7 м/с. Скорость звука с учётом диссипации энергии и теплообмена арпб159 на определенных участках претерпевает разрывы. Скачки происходят относительно изоэнтропного значения скорости звука.

Номер узл* СЯККГО) ОСИ X

Рис. 1. Закон изменения скорости звука в фиксированный момент времени вдоль канала в плоскости j = 6

Скачки скорости звука будут приводить к нарушению линейного закона Гука, связывающего изменение давления с относительной объёмной деформацией. Малые акустические возмущения плотности, возникающие в потоке вязкого теплопроводного газа, приведут к непропорциональным пульсациям давления, что необходимо учитывать при анализе возникновения турбулентности (Воронков, 2011).

Литература

1. Воронков С. С. О скорости звука в потоке вязкого газа с поперечным сдвигом. Электронный журнал «Техническая акустика». № 5. 2004. URL: http://www.ejta.org.

2. Воронков С. С. Зависимость скорости звука в потоке вязкого газа от различных факторов. Сборник трудов XVI сессии Российского акустического общества. М. : ГЕОС, 2005. Т. 1. С. 262-265.

3. Воронков С.С. О возникновении турбулентности в вязком теплопроводном газе. Электронный журнал «Техническая акустика» № 12. 2011. URL: http://www.ej ta.org.

4. Лойцянский Л. Г. Механика жидкости и газа. 5-е изд. М. : Наука, 1978.

5. Ньютон И. Математические начала натуральной философии. М. : Наука. 1989.

6. Роуч П. Вычислительная гидродинамика. М. : Мир, 1980. 616 с.

7. Рэлей. Теория звука. Т. II. М. : Изд-во техн.-теор. лит., 1955.

S. S. Voronkov

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

ABOUT THE SPEED OF SOUND IN GASES

Various formulas for the velocity of sound in gases are considered. It is noted that the flow of a viscous heat-conducting gas with a transverse shift is necessary to the influence of energy dissipation and heat transfer at the speed of sound in the analysis of turbulence.

Keywords: speed of sound, a viscous heat-conducting gas, the arising of turbulence.

Воронков Сергей Семенович — заведующий кафедрой «Автомобильные дороги» ФГБОУ ВПО ПсковГУ, канд. техн. наук, доцент, vorss60@yandex.ru.

Источник

Скорость звука в идеальном газе определяется следующим уравнением:

$V_{s}=sqrt{frac{gamma R T}{M} }$ ,

где
R — универсальная газовая постоянная, 8.314 Дж/(моль К)
T — абсолютная температура, К
M — молекулярная масса газа, кг/моль
гамма — показатель адиабаты газа.

Калькулятор, рассчитывающий скорость звука в газе, ниже.
Значения по умолчанию в нем (показатель адиабаты 1.4 и молекулярная масса 28.95) соответствуют сухому воздуху.

Что касается показателя адиабаты, то для одноатомного идеального газа он равен 5/3, для двухатомного — 7/5, для трехатомного — 4/3, и для более сложных молекул определяется числом степеней свободы конкретной молекулы.

Для гелия, например, с показателем адиабаты 5/3 и молекулярной массой 4, скорость звука будет равна 1007 м/с. Именно поэтому голос звучит так забавно, если надышаться гелием.

Скорость звука в газе

Температура, градусов Цельсия

Молекулярная масса газа, г/моль

Точность вычисления

Знаков после запятой: 2

Источник