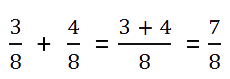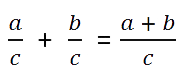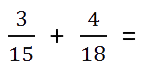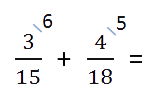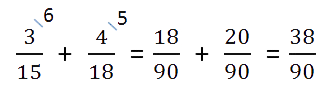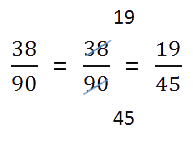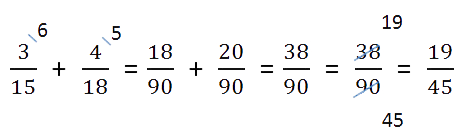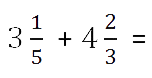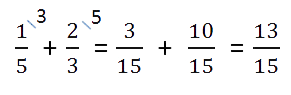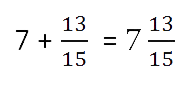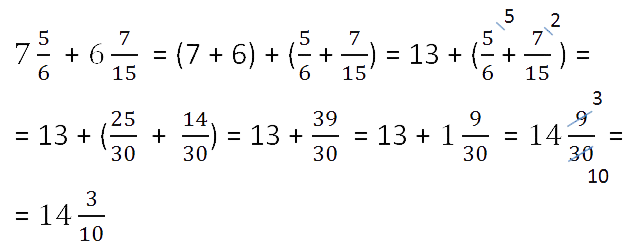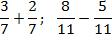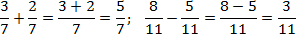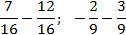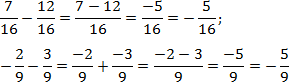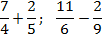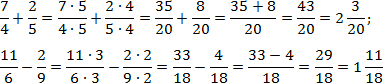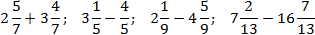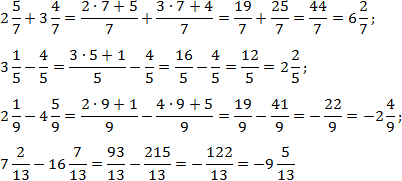Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Уравнения, содержащие переменную в знаменателе можно решать двумя способами:
-
Приведя дроби к общему знаменателю
-
Используя основное свойство пропорции
Вне зависимости от выбранного способа необходимо после нахождения корней уравнения выбрать из найденных допустимые значения, т.е те, которые не обращают знаменатель в $0$.
1 способ. Приведение дробей к общему знаменателю.
Пример 1
$frac{2x+3}{2x-1}=frac{x-5}{x+3}$
Решение:
1.Перенесем дробь из правой части уравнения в левую
[frac{2x+3}{2x-1}-frac{x-5}{x+3}=0]
Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей.
2.Теперь отметим что у дробей разные знаменатели, значит для того, чтобы составить разность необходимо привести дроби к общему знаменателю. Общим знаменателем будет произведение многочленов, стоящих в знаменателях исходных дробей: $(2x-1)(x+3)$
Для того чтобы получить тождественное выражение, числитель и знаменатель первой дроби необходимо умножить на многочлен $(x+3)$, а второй на многочлен $(2x-1)$.
[frac{(2x+3)(х+3)}{(2x-1)(х+3)}-frac{(x-5)(2х-1)}{(x+3)(2х-1)}=0]
Выполним преобразование в числителе первой дроби-произведем умножение многочленов. Вспомним , что для этого необходимо умножить первое слагаемое первого многочлена умножить на каждое слагаемое второго многочлена, затем второе слагаемое первого многочлена умножить на каждое слагаемое второго многочлена и результаты сложить
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3={2х}^2+6х+3х+9]
Приведем подобные слагаемые в полученном выражении
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3={2х}^2+6х+3х+9=] [{=2х}^2+9х+9]
Выполним аналогично преобразование в числителе второй дроби-произведем умножение многочленов
$left(x-5right)left(2х-1right)=хcdot 2х-хcdot 1-5cdot 2х+5cdot 1={2х}^2-х-10х+5={2х}^2-11х+5$
Тогда уравнение примет вид:
[frac{{2х}^2+9х+9}{(2x-1)(х+3)}-frac{{2х}^2-11х+5}{(x+3)(2х-1)}=0]
Теперь дроби с одинаковым знаменателем, значит можно производить вычитание. Вспомним, что при вычитании дробей с одинаковым знаменателем из числителя первой дроби необходимо вычесть числитель второй дроби, знаменатель оставить прежним
[frac{{2х}^2+9х+9-({2х}^2-11х+5)}{(2x-1)(х+3)}=0]
Преобразуем выражение в числителе. Для того, чтобы раскрыть скобки, перед которыми стоит знак «-» надо изменить все знаки перед слагаемыми , стоящими в скобках на противоположные
[{2х}^2+9х+9-left({2х}^2-11х+5right)={2х}^2+9х+9-{2х}^2+11х-5]
Приведем подобные слагаемые
${2х}^2+9х+9-left({2х}^2-11х+5right)={2х}^2+9х+9-{2х}^2+11х-5=20х+4$
Тогда дробь примет вид
[frac{{rm 20х+4}}{(2x-1)(х+3)}=0]
3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.
[{rm 20х+4=0}]
Решим линейное уравнение:
$20x=-4$
$X=-0,2$
4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.
Поставим условие, что знаменатели не равны $0$
[2x-1ne 0 x+3ne 0]
х$ne 0,5$ х$ne -3$
Значит допустимы все значения переменных, кроме $-3$ и $0,5$.
Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.
Ответ:$-0,2.$
Теперь можем составить алгоритм решения уравнения, которое содержит переменную в знаменателе
Алгоритм решения уравнения, которое содержит переменную в знаменателе
-
Перенести все элементы из правой части уравнения в левую. Для получения тождественного уравнения необходимо изменить все знаки, стоящие перед выражениями в правой части на противоположные
-
Если в левой части мы получим выражение с разными знаменателями, то приводим их к общему, используя основное свойство дроби. Выполнить преобразования, используя тождественные преобразования и получить итоговую дробь равную $0$.
-
Приравнять числитель к $0$ и найти корни получившегося уравнения.
-
Проведем выборку корней, т.е. найти допустимые значения переменных, которые не обращают знаменатель в $0$.
2 способ. Используем основное свойство пропорции
Основным свойством пропорции является то, что произведение крайних членов пропорции равно произведению средних членов.
Пример 2
Используем данное свойство для решения этого задания
[frac{2x+3}{2x-1}=frac{x-5}{x+3}]
1.Найдем и приравняем произведение крайних и средних членов пропорции.
$left(2x+3right)cdot( x+3)=left(x-5right)cdot(2x-1)$
[{2х}^2+3х+6х+9={2х}^2-10х-х+5]
$9x+11x=5-9$
$20x=-4$
$X=-0,2$
Решив полученное уравнение, мы найдем корни исходного
2.Найдем допустимые значения переменной .
Из предыдущего решения (1 способ) мы уже нашли , что допустимы любые значения, кроме $-3$ и $0,5$.
Тогда, установив что найденный корень является допустимым значением, мы выяснили, что $-0,2$ будет являться корнем.
Ответ:$-0,2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Решение уравнений с переменной в знаменателе дроби
Вы будете перенаправлены на Автор24
Уравнения, содержащие переменную в знаменателе можно решать двумя способами:
Приведя дроби к общему знаменателю
Используя основное свойство пропорции
Вне зависимости от выбранного способа необходимо после нахождения корней уравнения выбрать из найденных допустимые значения, т.е те, которые не обращают знаменатель в $0$.
1 способ. Приведение дробей к общему знаменателю.
Решение:
1.Перенесем дробь из правой части уравнения в левую
Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей.
2.Теперь отметим что у дробей разные знаменатели, значит для того, чтобы составить разность необходимо привести дроби к общему знаменателю. Общим знаменателем будет произведение многочленов, стоящих в знаменателях исходных дробей: $(2x-1)(x+3)$
Для того чтобы получить тождественное выражение, числитель и знаменатель первой дроби необходимо умножить на многочлен $(x+3)$, а второй на многочлен $(2x-1)$.
Выполним преобразование в числителе первой дроби-произведем умножение многочленов. Вспомним , что для этого необходимо умножить первое слагаемое первого многочлена умножить на каждое слагаемое второго многочлена, затем второе слагаемое первого многочлена умножить на каждое слагаемое второго многочлена и результаты сложить
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3=<2х>^2+6х+3х+9]
Приведем подобные слагаемые в полученном выражении
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3=<2х>^2+6х+3х+9=] [<=2х>^2+9х+9]
Выполним аналогично преобразование в числителе второй дроби-произведем умножение многочленов
$left(x-5right)left(2х-1right)=хcdot 2х-хcdot 1-5cdot 2х+5cdot 1=<2х>^2-х-10х+5=<2х>^2-11х+5$
Тогда уравнение примет вид:
Теперь дроби с одинаковым знаменателем, значит можно производить вычитание. Вспомним, что при вычитании дробей с одинаковым знаменателем из числителя первой дроби необходимо вычесть числитель второй дроби, знаменатель оставить прежним
Преобразуем выражение в числителе. Для того, чтобы раскрыть скобки, перед которыми стоит знак «-» надо изменить все знаки перед слагаемыми , стоящими в скобках на противоположные
Приведем подобные слагаемые
Тогда дробь примет вид
3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.
Решим линейное уравнение:
4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.
Поставим условие, что знаменатели не равны $0$
Значит допустимы все значения переменных, кроме $-3$ и $0,5$.
Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.
Ответ:$-0,2.$
Теперь можем составить алгоритм решения уравнения, которое содержит переменную в знаменателе
Алгоритм решения уравнения, которое содержит переменную в знаменателе
Перенести все элементы из правой части уравнения в левую. Для получения тождественного уравнения необходимо изменить все знаки, стоящие перед выражениями в правой части на противоположные
Если в левой части мы получим выражение с разными знаменателями, то приводим их к общему, используя основное свойство дроби. Выполнить преобразования, используя тождественные преобразования и получить итоговую дробь равную $0$.
Приравнять числитель к $0$ и найти корни получившегося уравнения.
Проведем выборку корней, т.е. найти допустимые значения переменных, которые не обращают знаменатель в $0$.
2 способ. Используем основное свойство пропорции
Основным свойством пропорции является то, что произведение крайних членов пропорции равно произведению средних членов.
Используем данное свойство для решения этого задания
1.Найдем и приравняем произведение крайних и средних членов пропорции.
Решив полученное уравнение, мы найдем корни исходного
2.Найдем допустимые значения переменной .
Из предыдущего решения (1 способ) мы уже нашли , что допустимы любые значения, кроме $-3$ и $0,5$.
Тогда, установив что найденный корень является допустимым значением, мы выяснили, что $-0,2$ будет являться корнем.
Ответ:$-0,2.$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 05 2021
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Сложение дробей
Поддержать сайт
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают
числители, а знаменатель оставляют тот же.
Пример.
C помощью букв это правило сложения можно записать так:
Запомните!
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться
следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти
наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
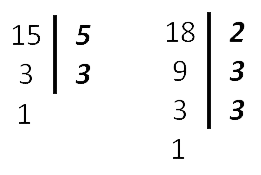
Как найти общий знаменатель
Находим НОК (15, 18).
НОК (15, 18) = 3 · 2 · 3 · 5 = 90
- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1)
делим по очереди на знаменатель каждой дроби.Полученные числа и будут дополнительными множителями
для каждой из дробей. Множители записываем над числителем дроби справа сверху.90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
- Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь
основным свойством дроби.После умножения в знаменателях
обеих дробей должен получиться наименьший общий знаменатель.
Затем складываем дроби как дроби с одинаковыми знаменателями.
- Проверяем полученную дробь.
- Eсли в результате получилась
неправильная дробь,
результат записываем в виде смешанного числа. Проверим нашу
дробь.38 < 90
У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
- Eсли в результате получилась
- Ещё раз весь пример целиком.
Сложение смешанных чисел
Сочетательное и переместитительное свойства сложения позволяют привести
сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.
Чтобы сложить смешанные числа нужно.
- Отдельно сложить их целые части.
Пример.
Складываем целые части.
- Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то
сначала приводим их к общему знаменателю, а затем складываем. - Сложить полученные результаты из пунктов 1 и 2.
- Если при сложении дробных частей получилась неправильная дробь, то нужно
выделить целую часть из этой дроби и прибавить к полученной
в пункте 1 целой части.
Ещё один пример на сложение смешанных чисел.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 декабря 2018 в 11:19
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
Baur Nurgazinov
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
2 января 2019 в 14:18
Ответ для Baur Nurgazinov
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
Лина Аникеева
Профиль
Благодарили: 0
Сообщений: 2
1) приводим все дроби к общему знаменателю
(2 -1 ) · х=
2) Вычислаем разность в скобках
( — ) · х=
· х=
сократим дроби на 3
· х=
3) вычисляем х
х= :
По правилу деления дробей делитель переворачиваем
x= · =
4 — сокращаем
х=3
Проверка:
(2 -1 ) · 3=( — ) · 3= · 3= · 3 = · = =
Ответ верный
0
Спасибо
Ответить
24 января 2017 в 19:44
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
Фанис Газизов
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
24 января 2017 в 21:12
Ответ для Фанис Газизов
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
Marina Kazakova
Профиль
Благодарили: 0
Сообщений: 1
?
0
Спасибо
Ответить
1 марта 2016 в 18:39
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
Денис Демидов
Профиль
Благодарили: 0
Сообщений: 1
спасибо сайт класс тему не понял
| было очень непонятно |
| теперь понятно + + |
+ + + + · + + + + +
0
Спасибо
Ответить
19 сентября 2016 в 13:05
Ответ для Денис Демидов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
6 февраля 2016 в 18:54
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Денис Бочин
Профиль
Благодарили: 0
Сообщений: 1
Сложи
числа 30 и
числа 14.
0
Спасибо
Ответить
10 февраля 2016 в 19:03
Ответ для Денис Бочин
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
Алексей Пешков
Профиль
Благодарили: 0
Сообщений: 2
1) от 30=;
2)
от 14=
2)
+ ===24=24
0
Спасибо
Ответить
14 января 2016 в 15:31
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
Анжела Волк
Профиль
Благодарили: 0
Сообщений: 1
2/6 или1/2 сравнение дробей
0
Спасибо
Ответить
14 января 2016 в 18:05
Ответ для Анжела Волк
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
Александр Хан
Профиль
Благодарили: 0
Сообщений: 1
больше
0
Спасибо
Ответить
19 сентября 2016 в 10:33
Ответ для Анжела Волк
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Отрицательное число всегда меньше положительного =)
0
Спасибо
Ответить
27 декабря 2015 в 20:00
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
Надежда Егина
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
19 сентября 2016 в 10:07
Ответ для Надежда Егина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
· a12· b4 · · a8· b5 = · a20 · b9=125· a20 · b9При раскрытии скобок отбросил знак ?, т.к. степень чётная, а значит получится +.
0
Спасибо
Ответить
21 апреля 2015 в 15:17
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
Алина Гимадеева
Профиль
Благодарили: 0
Сообщений: 2
1) 15 — 7
4/7= 2) 20
4/5 — 1
5/6 *
1/3
3) 5
1/3 + 4
1/3 +
2/5
0
Спасибо
Ответить
14 апреля 2016 в 12:32
Ответ для Алина Гимадеева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Судя по всему, не разобрались с использованием кнопки дробь. Интерпретирую задачу следующим образом:
1) 15 ? 7
=8
2) 20
? 1 · = ? = = = =9 — похоже ошибка в примере, он гораздо сложнее двух других.
3) 5
+4 + = 9 + = + = = =10
0
Спасибо
Ответить
7 апреля 2015 в 20:06
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
Александр Гридюшко
Профиль
Благодарили: 0
Сообщений: 1
как решить?4
+
0
Спасибо
Ответить
7 апреля 2015 в 21:13
Ответ для Александр Гридюшко
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
Анастасия Власова
Профиль
Благодарили: 0
Сообщений: 1
4+ = + = + = = = = 6
0
Спасибо
Ответить
14 апреля 2015 в 16:55
Ответ для Александр Гридюшко
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
4 + = + = = =16:3=1
0
Спасибо
Ответить
16 апреля 2015 в 19:06
Ответ для Александр Гридюшко
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Мирон Федоров
Профиль
Благодарили: 0
Сообщений: 1
Asel не правильно
0
Спасибо
Ответить
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Содержание
- Сложение и вычитание дробей
- Что делать, если знаменатели разные
- Что делать, если у дроби есть целая часть
- Резюме: общая схема вычислений
- Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Как найти общий знаменатель
- Дроби. Сложение дробей.
- Сложение дробей с одинаковыми знаменателями.
- Сложение дробей с разными знаменателями.
- Сложение смешанных чисел (смешанных дробей).
- Сложение десятичных дробей.
- Сложение дробей: теория и практика
- Понятие дроби
- Основные свойства дробей
- Как плюсовать дроби
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
- Сложение смешанных чисел
Сложение и вычитание дробей
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Источник
Сложение дробей
При сложении дробей могут встретиться разные случаи.
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
C помощью букв это правило сложения можно записать так:
Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Сложение дробей с разными знаменателями
Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.
- Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.
Пример. Сложить дроби.
Как найти общий знаменатель
Находим НОК (15, 18) .

- Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби.
Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху.
90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби.
После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями.
Проверяем полученную дробь.
- Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь.
Источник
Дроби. Сложение дробей.
Сложение дробей с одинаковыми знаменателями.
Чтоб сложить 2 дроби с одинаковыми знаменателями, необходимо сложить их числители, а знаменатели оставить без изменений. Сложение дробей , примеры :
Общая формула для сложения обыкновенных дробей и вычитания дробей с одинаковыми знаменателями:
Обратите внимание! Проверьте нельзя ли сократить дробь, которую вы получили, записывая ответ.
Сложение дробей с разными знаменателями.
Правила сложения дробей с разными знаменателями:
- приводим дроби к наименьшему общему знаменателю (НОЗ). Для этого находим наименьшееобщее кратное (НОК) знаменателей;
- складываем числители дробей, а знаменатели оставляем не меняя;
- сокращаем дробь, которую получили;
- если получили неправильная дробь – преобразовываем неправильную дробь в смешанную дробь.
Примеры сложения дробей с разными знаменателями:
Сложение смешанных чисел (смешанных дробей).
Правила сложения смешанных дробей:
- приводим дробные части этих чисел к наименьшему общему знаменателю (НОЗ);
- отдельно складываем целые части и отдельно дробные части, складываем результаты;
- если при сложении дробных частей получили неправильную дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части;
- сокращаем полученную дробь.
Пример сложения смешанной дроби :
Сложение десятичных дробей.
При сложении десятичных дробей процесс записывают «столбиком» (как обычное умножение столбиком), так чтобы одноимённые разряды находились друг под другом без смещения. Запятые обязательно выравниваем чётко друг под другом.
Правила сложения десятичных дробей:
1. Если нужно, уравниваем количество знаков после запятой. Для этого добавляем нули к необходимой дроби.
2. Записываем дроби так, чтобы запятые находились друг под другом.
3. Складываем дроби, не обращая внимания на запятую.
4. Ставим запятую в сумме под запятыми, дробей, которые складываем.
Обратите внимание! Когда у заданных десятичных дробей разное количество знаков (цифр) после запятой, то к дроби, у которой меньше десятичных знаков приписываем нужное количество нулей, для уравнения в дробях число знаков после запятой.
Разберёмся на примере. Найти сумму десятичных дробей:
Уравниваем число знаков после запятой в десятичных дробях. Дописываем 2 нуля справа к десятичной дроби 13,7 .
Если сложение десятичных дробей вы освоили достаточно хорошо, то недостающие нули можно дописывать в уме.
Источник
Сложение дробей: теория и практика
О чем эта статья:
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 14.
Основные свойства дробей
1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Равными называются такие a/b и c/d, если:
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.
Источник